Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).
Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.
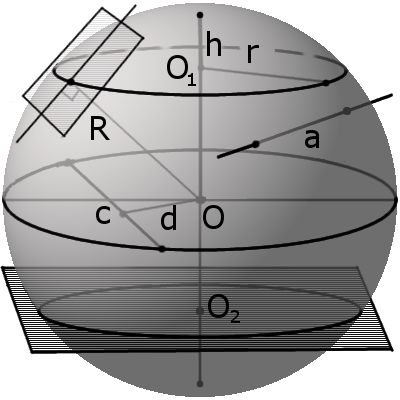
Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).
Радиус сферы (шара) (R) - это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).
Диаметр сферы (шара) (D) - это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.
Площадь поверхности сферы через радиус или диаметр: S = 4πR2 = πD2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:
x2 + y2 + z2 = R2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x0, y0, z0) в декартовой системе координат:
(x - x0)2 + (y - y0)2 + (z - z0)2 = R2
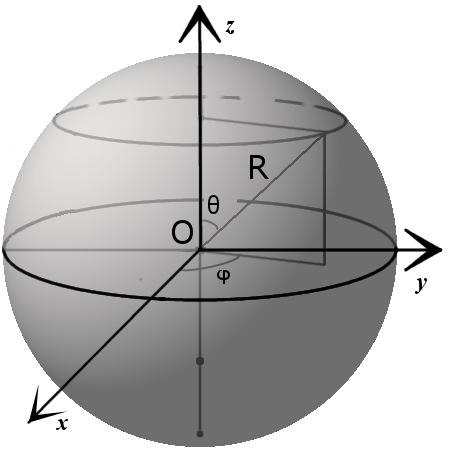
3. Параметрическое уравнение сферы с центром в точке (x0, y0, z0):
x = x0 + R · sin θ · cos φy = y0 + R · sin θ · sin φz = z0 + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].



















