ГОСУДАРСТВЕННОЕ ОБЛАСТНОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ЛИПЕЦКИЙ ПОЛИТЕХНИЧЕСКИЙ ТЕХНИКУМ»

Методическая разработка урока
по дисциплине «Математика»
по теме
«Матрицы и определители. Элементарные преобразования матрицы»
по программе подготовки специалистов среднего звена
Разработала: преподаватель математики
Клещина Н.В.
Липецк, 2020
Пояснительная записка:
Изучение математики направлено на достижение, в первую очередь, целей интеллектуального развития студентов, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Все люди на нашей планете погружены в Матрицы . Матрицы как бы пронизывают нашу реальность в каждом ее проявлении. Каждый из нас на протяжении всей своей жизни и в любой ее момент находится в какой-либо из Матриц. С помощью Матриц можно объяснить, почему человек не может достичь успеха в каком-то деле, почему он болеет или почему у него нет шансов добиться успеха вообще, рассчитать количество продукции, месячные и годовые выручки.
В структуре изучаемой дисциплины «Математика» выделяется следующий раздел: «Основы линейной алгебры». Содержание раздела «Основы линейной алгебры » включает тему урока «Матрицы и определители. Элементарные преобразования матрицы» .
В результате изучения данной темы студент должен
Знать:
определение матрицы, виды и свойства матриц;
определение определителя матриц, методы нахождения определителя;
Уметь:
• определять определитель матрицы;
• решать прикладные задачи с применением матриц;
Тема урока : Матрицы и определители. Элементарные преобразования матрицы.
Цели урока:
Образовательные:
- сформировать умения и навыки понятия матрицы и ее виды, определитель матрицы
- сформировать умения операции сложения, вычитания, умножения матрицы на число и
матрицы на матрицу, возведение в степень, нахождение обратной матрицы;
Развивающие:
- содействовать развитию у учащихся мыслительных операций: умение анализировать,
синтезировать, сравнивать;
- отрабатывать навыки самооценивания знаний и умений, выбора заданий,
соответствующего уровню мыслительной деятельности;
- формировать и развивать умения и навыки: обобщение, поиск способов решения.
Воспитательные:
- воспитание личных качеств, обеспечивающих успешность творческой деятельности;
- воспитание требовательности, принципиальности, самокритичности, благородства,
чувства товарищества.
Тип урока: Урок ознакомления с новым материалом.
Межпредметные связи: физика, информатика, история
Оборудование и наглядные средства обучения: компьютерный класс с ОС Windows 8 и пакетом программ Microsoft Office 2010 (10 ПК), мультимедийный проектор, интерактивная доска SmartBoard, программа Notebook, колонки.
Методическая цель: способы активизации мыслительной деятельности студентов
Ход урока:
I.Организационный момент: Подготовка студентов к уроку (проверка отсутствующих на уроке, наличие тетрадей)
II. Сообщение темы и целей урока.
Сообщение темы и цели урока (понятие матрицы и основанный на нем раздел математики – матричная алгебра – имеют важное значение, так как значительная часть математических моделей экономических объектов и процессов записывается в достаточно простой, а главное – компактной матричной форме).
Итак, цель сегодняшнего урока: рассмотреть понятия матрицы и ее виды, определитель матрицы ,сформировать умения операции сложения, вычитания, умножения матрицы на число и матрицы на матрицу, возведение в степень, нахождение обратной матрицы.
III. Изучение нового материала
3.1 Теоретический материал
1.Определение (в тетрадь) Матрицей размера mn, где m- число строк, n- число столбцов, называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определяется номером строки и столбца, на пересечении которых он находится. Элементы матрицы обозначаются aij, где i- номер строки, а j- номер столбца.
А = 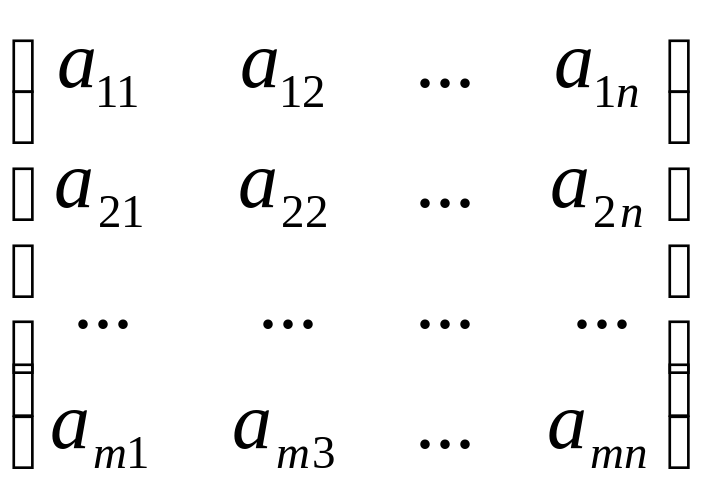
Основные действия над матрицами.
Матрица может состоять как из одной строки, так и из одного столбца. Вообще говоря, матрица может состоять даже из одного элемента.
Определение (в тетрадь )Если число столбцов матрицы равно числу строк (m=n), то матрица называется квадратной.
Определение (в тетрадь ) Матрица вида:
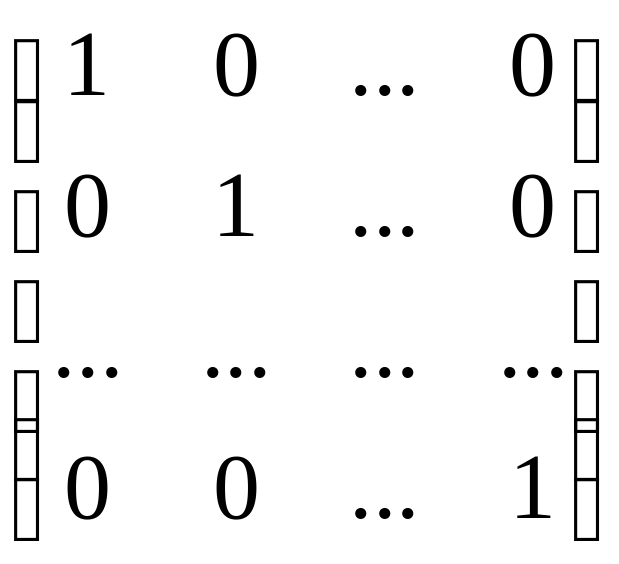 = E,
= E,
называется единичной матрицей.
Определение. Если amn = anm , то матрица называется симметрической.
Пример. 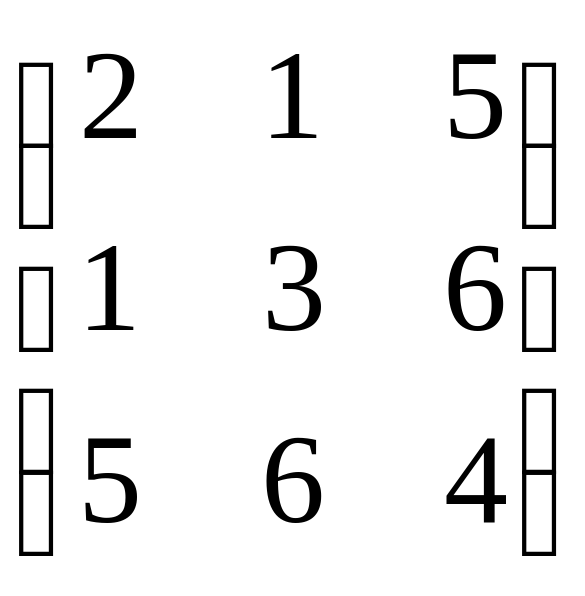 - симметрическая матрица
- симметрическая матрица
Определение(в тетрадь ) Квадратная матрица вида  называется диагональной матрицей.
называется диагональной матрицей.
2.Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:
Определение(в тетрадь ) Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

cij = aij bij
С = А + В = В + А.
Операция умножения (деления) матрицы любого размера на произвольное число сводится к умножению (делению) каждого элемента матрицы на это число.
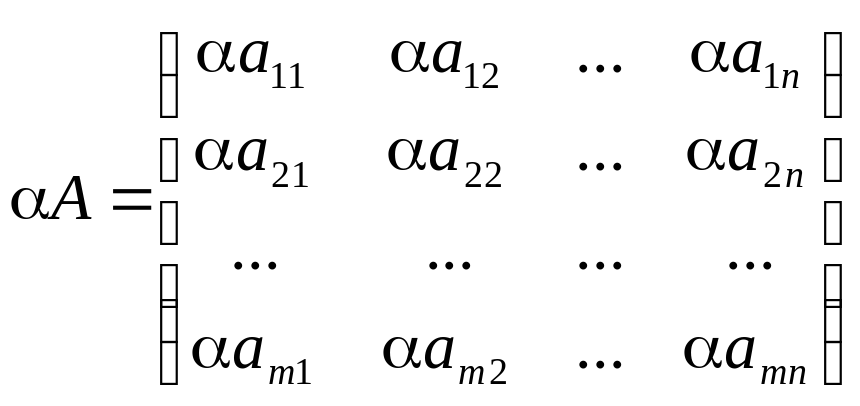
(А+В) =А В А() = А А
3.Операция умножения матриц.
Определение(в тетрадь ): Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:
AB = C; 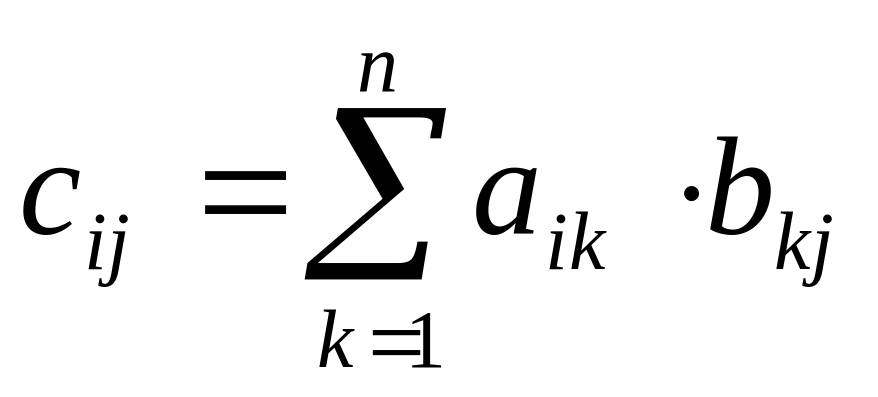 .
.
Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.
Свойства операции умножения матриц. (в тетрадь 1-6 )
1)Умножение матриц не коммутативно, т.е. АВ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.
Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.
Перестановочными могут быть только квадратные матрицы одного и того же порядка.
АЕ = ЕА = А
Очевидно, что для любых матриц выполняются следующее свойство:
AO = O; OA = O,
где О – нулевая матрица.
2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:
(АВ)С=А(ВС).
3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно:
А(В + С) = АВ + АС
(А + В)С = АС + ВС.
4) Если произведение АВ определено, то для любого числа верно соотношение:
(AB) = (A)B = A(B).
5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство:
(АВ)Т = ВТАТ, где
индексом Т обозначается транспонированная матрица.
6) Заметим также, что для любых квадратных матриц det (AB) = detAdetB.
Что такое det будет рассмотрено ниже.
Определение (в тетрадь ). Матрицу В называют транспонированной матрицей А, а переход от А к В транспонированием, если элементы каждой строки матрицы А записать в том же порядке в столбцы матрицы В.
А = 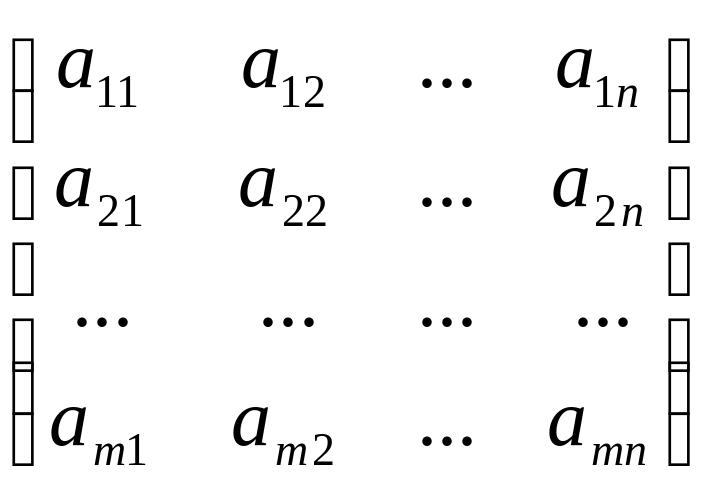 ; В = АТ=
; В = АТ=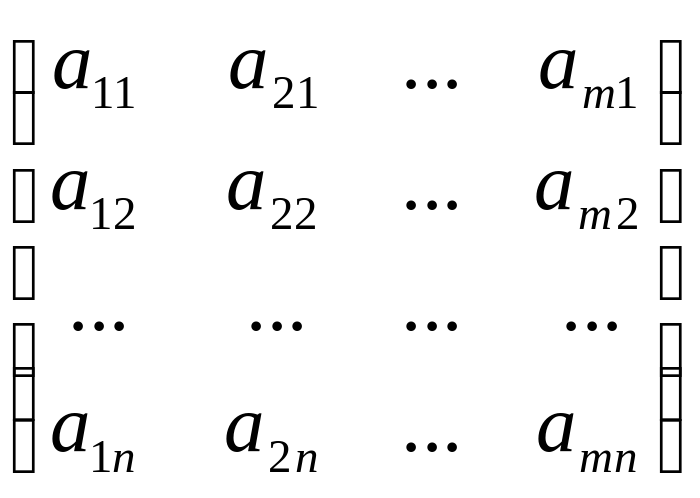 ;
;
другими словами, bji = aij.
В качестве следствия из предыдущего свойства (5) можно записать, что:
(ABC)T = CTBTAT,
при условии, что определено произведение матриц АВС.
4.Определители (детерминанты). Определение (в тетрадь ) Определителем квадратной матрицы А= называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле:
det A = 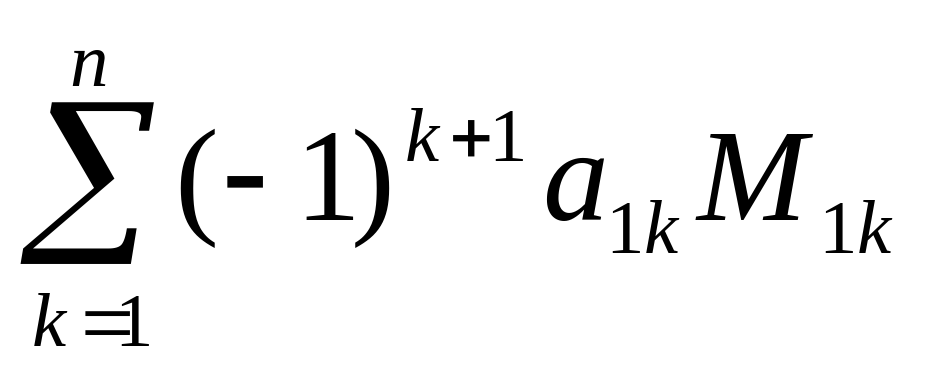 , где (1)
, где (1)
М1к – детерминант матрицы, полученной из исходной вычеркиванием первой строки и k – го столбца. Следует обратить внимание на то, что определители имеют только квадратные матрицы, т.е. матрицы, у которых число строк равно числу столбцов.
Формула (1) позволяет вычислить определитель матрицы по первой строке, также справедлива формула вычисления определителя по первому столбцу:

det A = 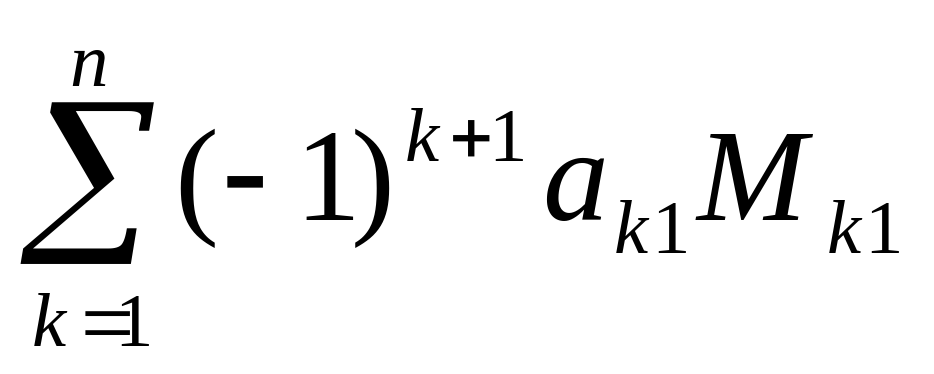 (2)
(2)
Вообще говоря, определитель может вычисляться по любой строке или столбцу матрицы, т.е. справедлива формула:
detA = 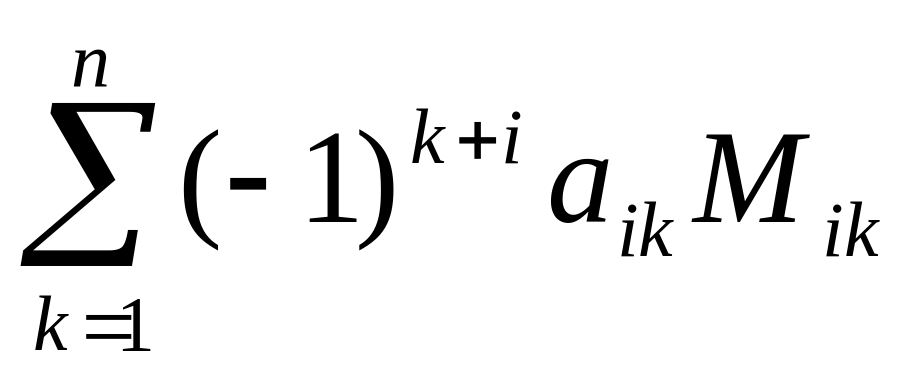 , i = 1,2,…,n. (3)
, i = 1,2,…,n. (3)
Очевидно, что различные матрицы могут иметь одинаковые определители.
Определитель единичной матрицы равен 1.
Для указанной матрицы А число М1к называется дополнительным минором элемента матрицы a1k. Таким образом, можно заключить, что каждый элемент матрицы имеет свой дополнительный минор. Дополнительные миноры существуют только в квадратных матрицах.
Определение (в тетрадь ) Дополнительный минор произвольного элемента квадратной матрицы aij равен определителю матрицы, полученной из исходной вычеркиванием i-ой строки и j-го столбца.
Свойство1. Важным свойством определителей является следующее соотношение:
det A = det AT;
Свойство 2. det ( A B) = det A det B.
Свойство 3. det (AB) = detAdetB
Свойство 4. Если в квадратной матрице поменять местами какие-либо две строки (или столбца), то определитель матрицы изменит знак, не изменившись по абсолютной величине.
Свойство 5. При умножении столбца (или строки) матрицы на число ее определитель умножается на это число.
Свойство 6. Если в матрице А строки или столбцы линейно зависимы, то ее определитель равен нулю.
Определение: Столбцы (строки) матрицы называются линейно зависимыми, если существует их линейная комбинация, равная нулю, имеющая нетривиальные (не равные нулю) решения.
Свойство 7. Если матрица содержит нулевой столбец или нулевую строку, то ее определитель равен нулю. (Данное утверждение очевидно, т.к. считать определитель можно именно по нулевой строке или столбцу.)
Свойство 8. Определитель матрицы не изменится, если к элементам одной из его строк(столбца) прибавить(вычесть) элементы другой строки(столбца), умноженные на какое-либо число, не равное нулю.
Свойство 9. Если для элементов какой- либо строки или столбца матрицы верно соотношение: d = d1 d2 , e = e1 e2 , f = f1 f2 , то верно:
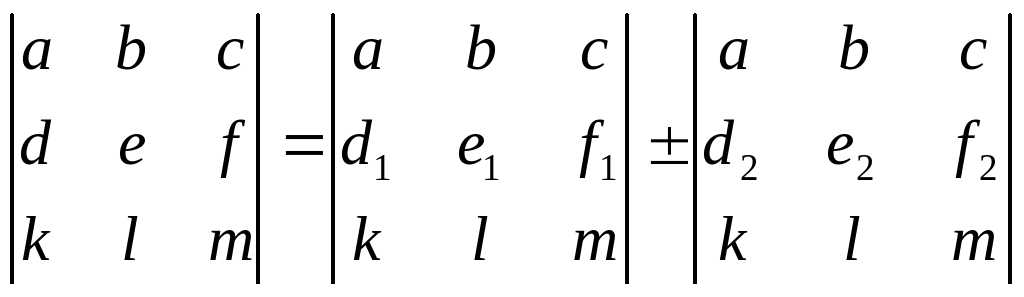
3.2 Практический материал
Задание 1. Даны матрицы А = 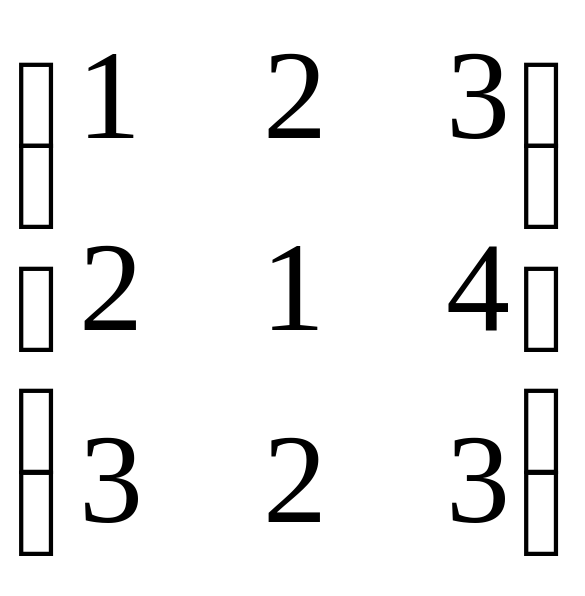 ; B =
; B = 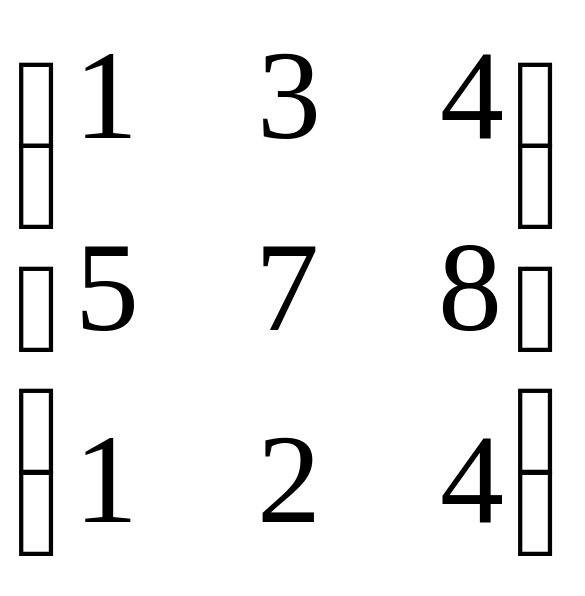 , найти 2А + В.
, найти 2А + В.
2А = 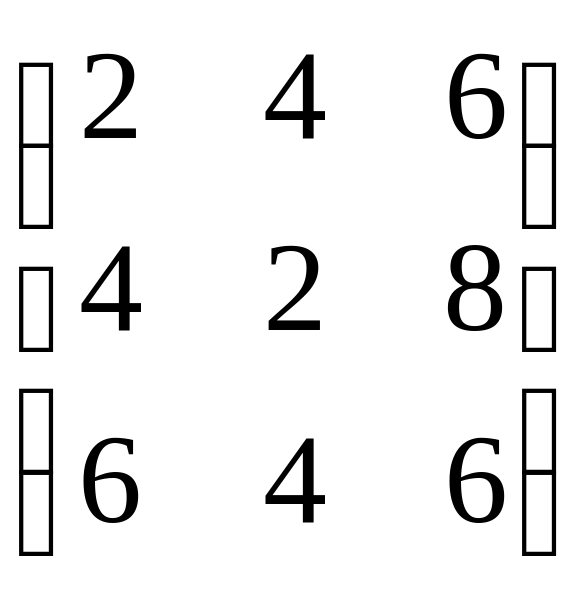 , 2А + В =
, 2А + В = 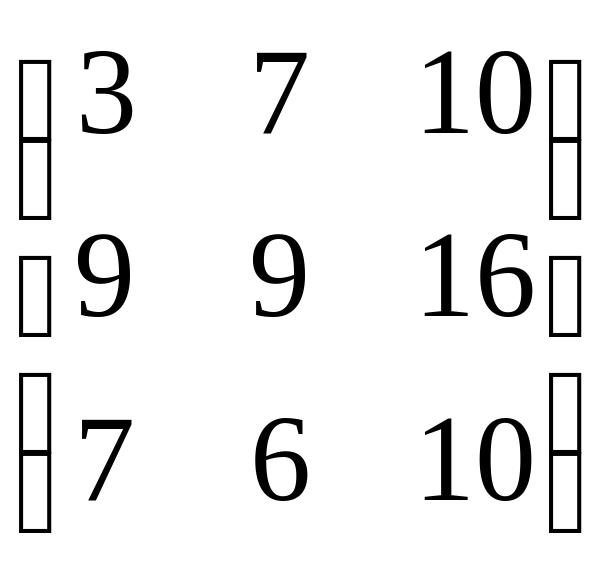 .
.
Задание 2. Найти произведение матриц А = 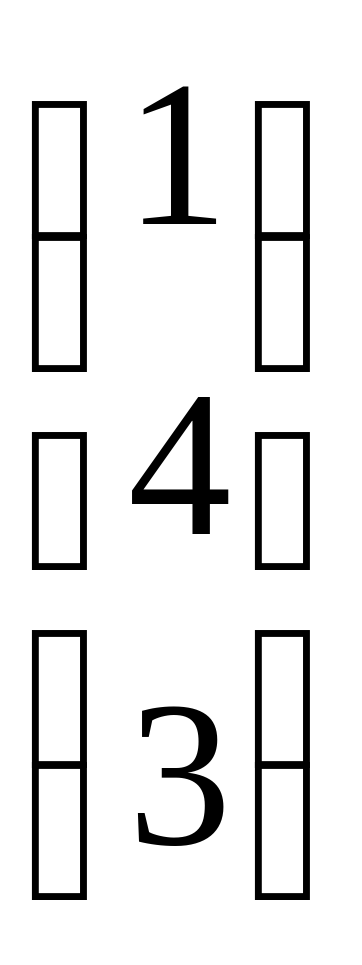 и В =
и В =  .
.
АВ = 
 =
= 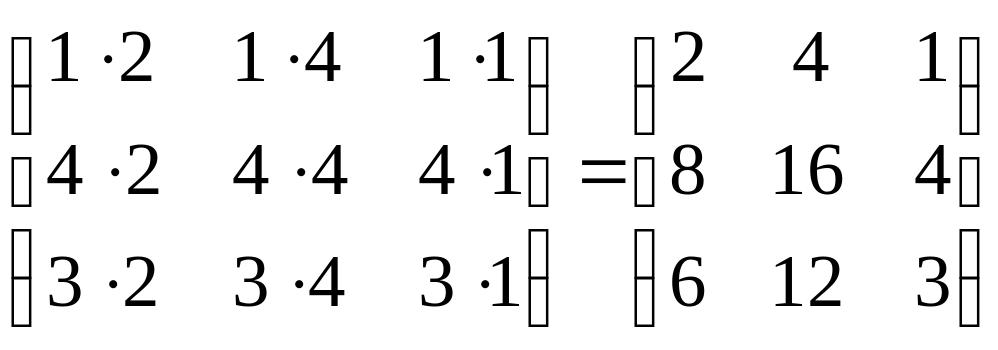 .
.
ВА = 
 = 21 + 44 + 13 = 2 + 16 + 3 = 21.
= 21 + 44 + 13 = 2 + 16 + 3 = 21.
Задание 3. Найти произведение матриц А= , В =
АВ = = = .
Задание 4.Даны матрицы А = , В = , С = и число = 2. Найти АТВ+С.
AT = ; ATB = = = ;
C = ; АТВ+С = + = .
Задание5.Вычислить определитель матрицы А =
= -5 + 18 + 6 = 19.
Задание 6. Даны матрицы А = , В = . Найти det (AB).
1-й способ: det A = 4 – 6 = -2; det B = 15 – 2 = 13; det (AB) = det A det B = -26.
2- й способ: AB = , det (AB) = 718 - 819 = 126 –
– 152 = -26.
3.3 Тест по вариантам
Вариант 1.
Задания уровня А:
1. Выберите единичную матрицу из числа предложенных:
1) � �
�
2) � �
�
3) � �
�
4) � �
�
2. Укажите матрицу � �, если матрица A=�
�, если матрица A=� �
�
1) � �
�
2) � �
�
3) � �
�
4) � �
�
3. Выберите вектор – столбец из числа предложенных матриц
1) � �
�
2) � �
�
3) � �;
�;
4)� �
�
4. Найдите сумму матриц � �, если �
�, если � � � �
� � �
1) � �
�
2)� �
�
3)� �;
�;
4) � �.
�.
5. Найдите сумму матриц � �, если � �
�, если � �
� �
�
� �;
�;
� �
�
� �
�
6. Найдите � �, если �
�, если � �
�
� �
�
� �
�
� �
�
� �
�
7. Найдите произведение матриц � �, если � �
�, если � �
произведение � � не определено;
� не определено;
� �
�
� �
�
� �
�
8. Найдите произведение матриц � �, если � �
�, если � �
1) � �;
2) � �
3) произведение � � не определено;
� не определено;
4) � �
9. Как изменится определитель при транспонировании матрицы?
1) определитель не изменится;
2 ) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -7;
2 ) -5;
3) 1;
4) 5.
11. Вычислите определитель 3-го порядка
1) 98;
2) -30;
3) 90;
4) 104.
12. Выберите невырожденную матрицу из числа предложенных
� �
�
� �
�
� �
�
�  �
�
13. Найдите минор m12 соответствующего элемента определителя
1) -2;
2) 13;
3) -5;
4) 5.
14. Найдите алгебраическое дополнение � � соответствующего элемента матрицы � �
� соответствующего элемента матрицы � �
-18;
-19;
18;
19.
15. Найдите значение � �, решив уравнение =0
�, решив уравнение =0
1) � �
�
2) 0;
3) � �
�
4) � �
�
Задания уровня В:
1 . Найдите матрицу, обратную данной � �
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
Вариант 2.
Задания уровня А:
1. Выберите треугольную матрицу из числа предложенных:
1) � �
�
2) � �
�
3)� �
�
4) � �
�
2. Укажите матрицу � �, если матрица � �
�, если матрица � �
1) � �
�
2) � �
�
3) � �
�
4) � �
�
3. Выберите вектор – строку из числа предложенных матриц
� �
�
� �
�
� �
�
� �
�
4. Найдите разность матриц � �, если � �
�, если � �
1) � �;
�;
2) � �;
�;
3)� �;
�;
4) � �
�
5. Найдите сумму матриц � �, если � �
�, если � �
� �
�
2) � �
3) � �;
�;
4) � �
6. Найдите � �, если � �
�, если � �
� �
�
� �
� �;
�;
� �
7. Найдите произведение матриц � �, если� �
�, если� �
1)� �
�
� �.
�.
� �
�
произведение � �не определено;
�не определено;
8. Найдите произведение матриц � �, если � �
�, если � �
1) произведение � � не определено;
� не определено;
2) � �
3) � �
4) � �
9 . Как изменится определитель при перестановке двух его параллельных рядов?
1) определитель не изменится;
2) знак определителя поменяется на противоположный;
3) значение определителя удвоится;
4) определитель примет значение, обратное исходному.
10. Вычислите определитель 2-го порядка
1) -17;
2 ) 13;
3) 3;
4) -13.
11. Вычислите определитель 3-го порядка
1) 92;
2) 72;
3) 56;
4) 54.
12. Выберите вырожденную матрицу из числа предложенных.
� �
�
� �
�
� �
�
� �
�
13. Найдите минор m21 соответствующего элемента определителя
1) -10;
2) 3;
3) 4;
4) -4.
14. Найдите алгебраическое дополнение А32 соответствующего элемента матрицы � �.
50;
9 ;
-50;
-9.
15. Найдите значение х, решив уравнение =0
1) 6;
2) 9;
3) 18;
4) -18.
Задания уровень В:
1 . Найдите матрицу, обратную данной � �
2. Решите систему линейных алгебраических уравнений
3. Вычислите определитель 4-го порядка
| Ключи |
| Вариант 1 | Вариант 2 |
| А1 2 | А1 1 |
| А2 4 | А2 2 |
| А3 4 | А3 3 |
| А4 2 | А4 1 |
| А5 1 | А5 2 |
| А6 4 | А6 2 |
| А7 3 | А7 4 |
| А8 1 | А8 2 |
| А9 1 | А9 2 |
| А10 4 | А10 4 |
| А11 1 | А11 3 |
| А12 3 | А12 1 |
| А13 4 | А13 3 |
| А14 3 | А14 3 |
| А15 1 | А15 4 |
|
|
|
|
В1 � �.
|
В1 � �.
|
| В2 (1;1;1).
| В2 (1; 0; 2).
|
| В3 - 26 | В3 -20.
|
IV. Итоги урока: Проверка теста, выставление оценок
V.Домашняя работа
1.Конспект
2. Даны матрицы . Выполните с заданными матрицами указанные действия  .
.
Решение.
Начинаем с умножения матрицы А на матрицу В:
Теперь умножаем единичную матрицу второго порядка Е на два:
Складываем две полученные матрицы:
Осталось выполнить операцию умножения полученной матрицы на матрицу А:
Интернет-ресурсы:
www.ziimag.narod.ru - персональный сайт автора Мордковича А. Г. "Практика развивающего обучения".
www.math.ru -Интернет
www.it-n.ru-Сеть творческих учителей. Материалы и ресурсы, касающиеся использования ИКТ в учебном процессе:
– библиотека готовых учебных проектов с применением ИКТ, а также различные проектные идеи, на основе которых можно разработать свой собственный проект;
– библиотека методик проведения уроков использованием разнообразных электронных
ресурсов;
– руководства и полезные советы по использованию программного обеспечения в учебном процессе;
– подборка ссылок на интересные аналитические и тематические статьи для педагогов.
www.exponenta.ru -Образовательный математический сайт. Содержит материалы по работе с математическими пакетами Mathcad, MATLAB, Mathematica, Maple и др. Методические разработки, примеры решения задач, выполненные с использованием математических пакетов. Форум и консультации для студентов и школьников.
http:school-collection.edu -Единая коллекция цифровых образовательных ресурсов. Цифровые образовательные ресурсы (ЦОР) к учебникам.
http://www.intellectcentre.ru – сайт издательства «Интеллект-Центр», -тренировочные материалы, демонстрационные версии, банк тренировочных заданий с ответами, методические рекомендации и образцы решений.
1







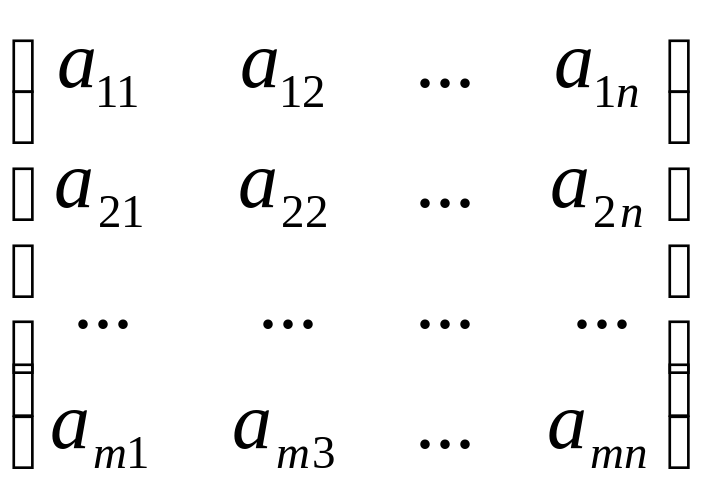
 = E,
= E, - симметрическая матрица
- симметрическая матрица называется диагональной матрицей.
называется диагональной матрицей.
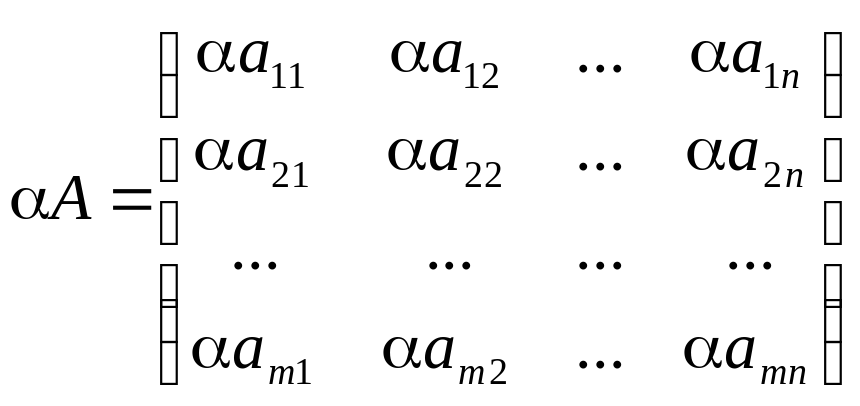
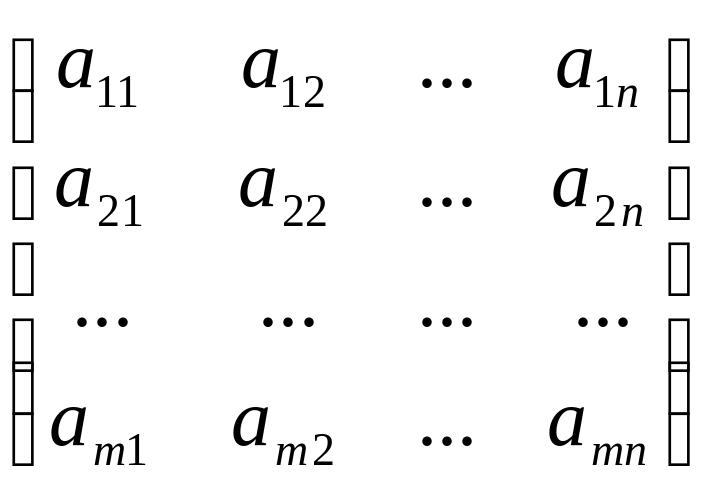 ; В = АТ=
; В = АТ=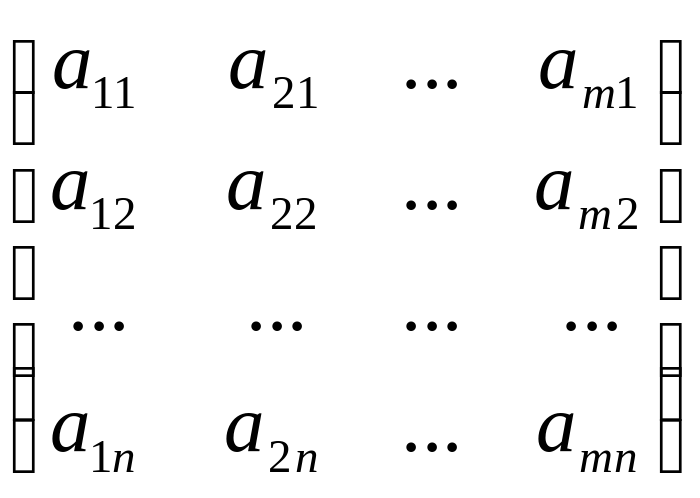 ;
; называется число, которое может быть вычислено по элементам матрицы по формуле:
называется число, которое может быть вычислено по элементам матрицы по формуле:
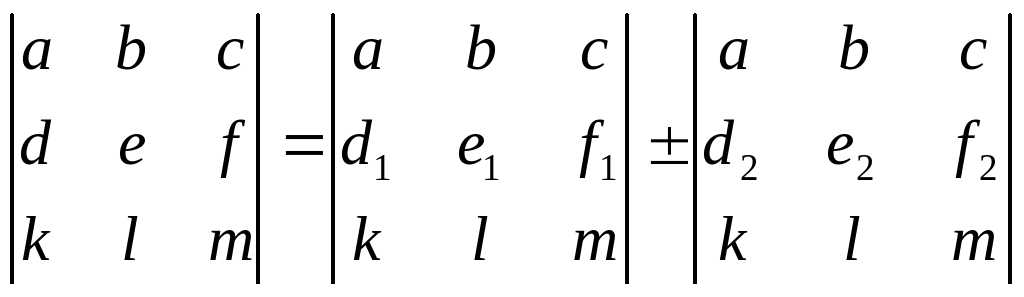
 ; B =
; B =  , найти 2А + В.
, найти 2А + В. , 2А + В =
, 2А + В =  .
.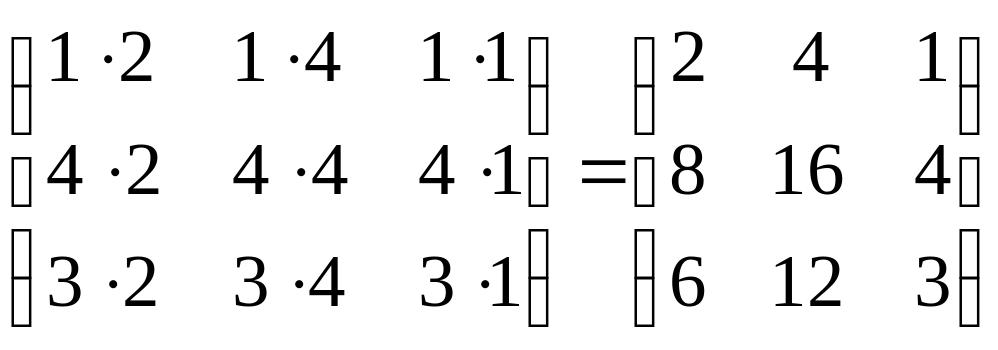 .
.









