Смотрите запись вебинара для учителей о современных инструментах, повышающих эффективность обучения в классе и дистанционно

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 18.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 12.06.2025 18:32

Авсеенко Людмила Михайловна

Преподаватель математики

9 799

4 325

Подписчики

Подписки

Местоположение

Россия, Нижний Тагил

Специализация

Информатика

Математика

Классному руководителю

Всем учителям

Прочее

Обо мне Блог Файлы Тесты Галерея Активность Награды

ПРАКТИЧЕСКАЯ РАБОТА «Операции над матрицами. Вычисление определителей»

Категория: Математика

27.03.2017 18:41

Цель практической работы: освоить способы выполнения операций над матрицами, элементарные преобразования матриц, вычисление определителя, нахождение обратной матрицы.

Просмотр содержимого документа
«ПРАКТИЧЕСКАЯ РАБОТА «Операции над матрицами. Вычисление определителей»»

ПРАКТИЧЕСКАЯ РАБОТА

«Операции над матрицами. Вычисление определителей»

Цель практической работы: освоить способы выполнения операций над матрицами, элементарные преобразования матриц, вычисление определителя, нахождение обратной матрицы.

Оценки выставляются по пятибальной шкале.

Критерии выставления оценок.

3 — если правильно решены любые пять заданий
4 — если правильно решены любые восемь заданий
5 — если правильно решено десять заданий

Задания.

Найти матрицу 2А.
Найти А+В.
Найти С = А-3В.
Вычислить А·В и В·А
Найти транспонированную матрицу
Найти минор М₂₃ к элементу а₂₃ определителя
Найти алгебраическое дополнение А₂₃ к элементу а₂₃ определителя.
Вычислить определитель матрицы
Найти обратную матрицу
Возвести матрицу в квадрат.

Данные:

Образец выполнения практической работы.

Задание 1.

Пусть

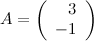Найти матрицу

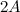Решение.

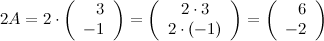
Ответ.

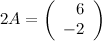
Задание 2.

Найти

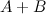, если

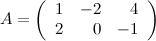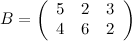
Решение.

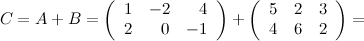
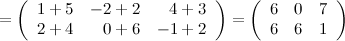
Ответ

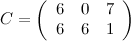
Задание 3. Найти матрицу ,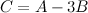

если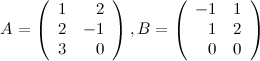

Решение.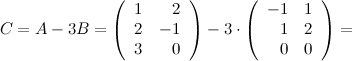

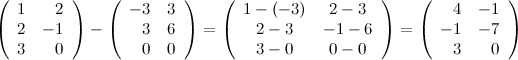
Ответ.

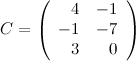
Задание 4. Вычислить 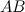и ,

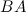если

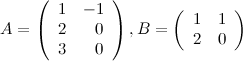
Решение. Так как 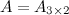, а 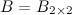, то произведение возможно и результатом операции умножения будет матрица 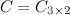, а это матрица вида .

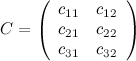Вычислим элементы матрицы :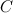

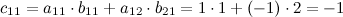
Итак, .

Выполним произведения в более компактном виде:

Найдем теперь произведение . Так как количество столбцов матрицы (первый сомножитель) не совпадает с количеством строк матрицы (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.

Ответ. . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы не совпадает с количеством строк матрицы .

Задание 5. Найти матрицу , если

Решение.

Ответ.

Задание 6. Найти минор к элементу определителя

Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

тогда

Ответ.

Задание 7. Найти алгебраическое дополнение к элементу определителя

Решение.

Ответ.

Задание 8. Вычислить определитель матрицы.

Решение.

Ответ.

Задание 9. Найти обратную матрицу к матрице

Решение. Вычисляем определитель матрицы:

Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица к матрице находится по формуле:

Найдем союзную матрицу , для этого вычислим алгебраические дополнения к элементам матрицы :

Таким образом,

Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

Итак,

Ответ.

Список рекомендуемой литературы

Богомолов Н.В., Математика, Учебник для ССУЗов . – М.: Дрофа. 2010. – 398 с.
Григорьев С.Г.Математика. Учебник для ССУЗов . – М.: Академия. 2010. – 384 с.
Башмаков М.И. Математика. Учебник для учреждений начального и среднего профессионального образования. – М.,: Академия. 2011. – 256 с.
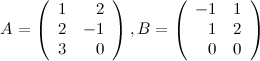
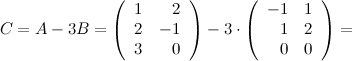
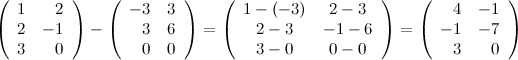
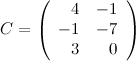
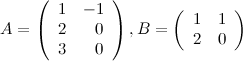
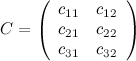