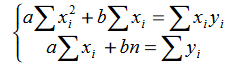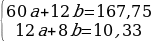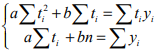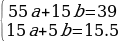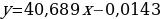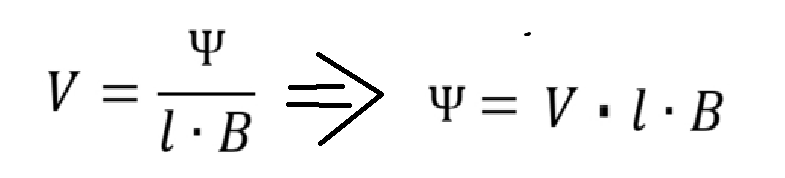Метод наименьших квадратов
Оглавление
Введение 3
Глава 1.Теория и практика МНК 4
1.1.Основа МНК 4
Глава 1.2.Виды функций 5
Глава 2.Примеры задач с методом МНК 6
Глава 2.1.Решение типовой задачи методом МНК 6
Глава 2.2.Решение задачи о прибыли фирмы с использованием МНК. 7
Глава 3.0.Метод МНК на практике 8
Глава 3.1.Код на PYTHON и его проверка. 9
Заключеиие 11
Интернет ресурсы 12
Введение
„В каждой естественной науке заключено столько истины, сколько в ней есть математики.“
Иммануил Кант
Метод наименьших квадратов (МНК) - это математический метод, который используется для аппроксимации экспериментальных данных линейной моделью. Он является одним из наиболее распространенных методов регрессионного анализа и широко применяется в различных областях науки, техники и экономики.
Основная идея МНК заключается в минимизации суммы квадратов отклонений между значениями наблюдаемых данных и значениями, предсказанными моделью. Этот метод позволяет оценить параметры модели таким образом, чтобы полученная линейная функция наилучшим образом соответствовала данным.
Используя метод наименьших квадратов, исследователи могут анализировать зависимости между переменными, делать прогнозы и выявлять взаимосвязи в данных. Этот метод является мощным инструментом статистического анализа и помогает сделать выводы на основе имеющихся данных.
Гипотеза исследования: по имеющимся экспериментальным точкам можно воспроизвести искомую зависимость
Актуальность выбранной темы: Метод наименьших квадратов (МНК) остается актуальным и востребованным инструментом в современной науке и практике в следующих областях:
Цель: исследовать метод наименьших квадратов
-
Изучить теоретическую составляющую метода наименьших квадратов;
-
С помощью метода наименьших квадратов по имеющимся экспериментальным точкам на примере наилучшим образом воспроизвести искомую зависимость;
-
Воспроизвести метод наименьших квадратов на языке программирования PYTHON;
Глава 1.Теория и практика МНК
В теории и на практике существуют задачи, в которых производится наблюдение за некой величиной. Будь то прибыль какой-либо фирмы, расписанная по месяцам, или рост ребенка в зависимости от лет его жизни.
В таких задачах существует зависимость между двумя переменными: месяцем и прибылью, годом и ростом. Эти данные получены экспериментально, и являются просто таблицей с числами, либо множеством точек на координатной плоскости.
Если же эксперимент не ограничивается ростом ребенка, а относится уже к довольно серьезным аналитическим расчетам, то появляется задача не просто описать экспериментальные данные, а получить строгую (хотя бы приближенную) зависимость одной переменной от другой. В дело вступает метод наименьших квадратов, он же МНК.
1.1.Основа МНК
Предположим, что предметом наблюдений (измерений) является величина у, значения которой меняются в зависимости от некоторого аргумента х. Общей задачей здесь является нахождение функции определенного вида, которая наилучшим образом отражает зависимость между величинами x и y. Эту зависимость обозначим, как 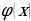
Суть метода наименьших квадратов сводится к тому чтобы сумма квадратов отклонений экспериментальных точек от значений, полученных теоретически обращалась в минимум:
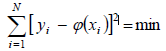
где 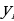 и
и 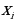 – экспериментальные значения переменных в i-том опыте, N – число опытов,
– экспериментальные значения переменных в i-том опыте, N – число опытов, 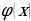 –искомая зависимость y от x.
–искомая зависимость y от x.
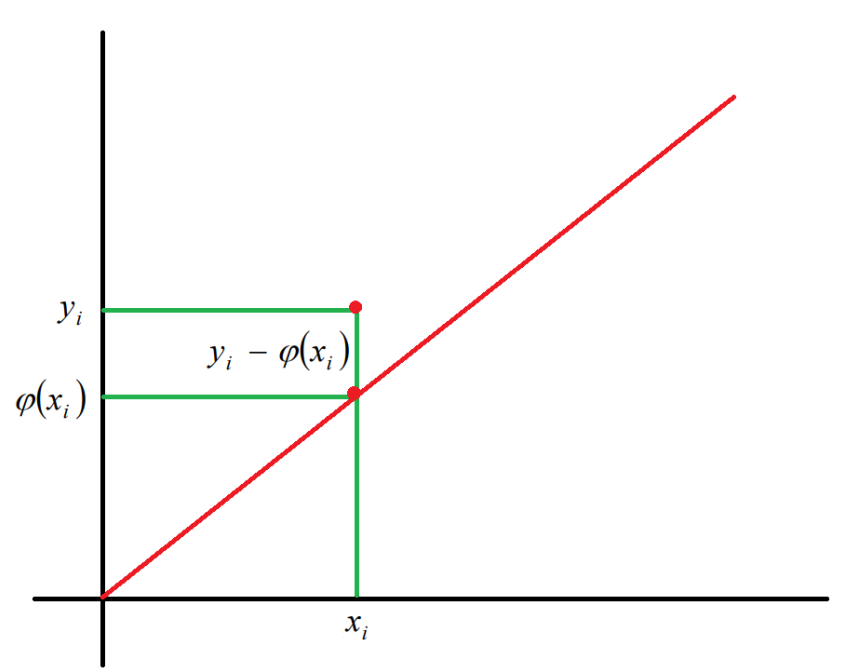
Рисунок 1 - Примерный график
Пример:
Красная линия-искомая теоретическая зависимость, в точке 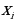 значение
значение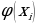 , а
, а 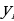 находится выше(экспериментальное значение).
находится выше(экспериментальное значение).
Нас интересует разница между ними, сумма квадратов этих разниц должна стремиться к минимуму
Глава 1.2.Виды функций
Искомая функция может быть любого вида, например:
-
линейная: y=ax+b
-
квадратичная: y=ax2+bx+c,
-
степенная: y=axn
-
экспоненциальная: y=aebx
-
логарифмическая: y=a∙ln(x)+b
-
гиперболическая: y=1/(ax+b) или y=a/x+b
Я же в данной работе рассмотрю в меру сложности лишь линейную зависимость вида y=ax+b
Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x. В результате измерений получается ряд значений:
x1, x2, ..., xi, , ... , xn;
y1, y2, ..., yi, , ... , yn.
По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую.
На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда
y = kx или y = a + bx.
Также для решения задач может использоваться система уравнений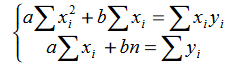
Где суммирование ведется по i от 1 до n, n = 8.
Глава 2.Примеры задач с методом МНК Глава 2.1.Решение типовой задачи методом МНК
Пример 1
Методом наименьших квадратов для данных, представленных в таблице, найти линейную
Зависимость y=ax+b
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| xi | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| yi | -11,47 | -7,59 | -4,32 | -0,41 | 3,01 | 6,91 | 10,12 | 14,08 |
У нас дана таблица, с помощью нее мы сможем найти ответ на данную задачу
Используя вышеприведённую систему уравнений, мы составляем расчетную таблицу:
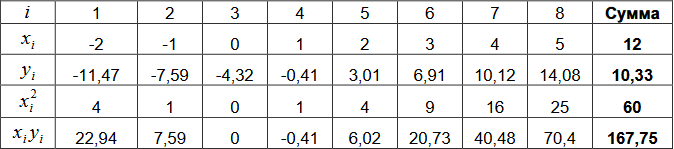
В ней мы сделали действия чтоб узнать недостающие элементы для системы уравнений
n=количество
Подставляя значения, данные в таблице получаем систему
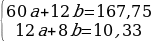
Решив систему(рис.1) получаем a=3,625, b=-4,146, отсюда получаем функцию y=3,625x-4,146
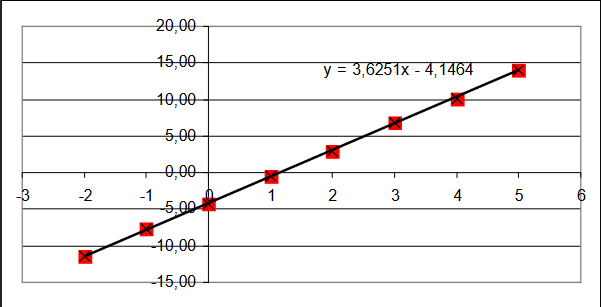
Рисунок 2 - График для примера 1
Ответ: y=3,625x-4,146.
Глава 2.2.Решение задачи о прибыли фирмы с использованием МНК.
Пример 2.
Прибыль фирмы за некоторый период деятельности по годам приведена ниже:
Год 1 2 3 4 5
Прибыль 3,9 4,9 3,4 1,4 1,9
Составьте линейную зависимость прибыли по годам деятельности фирмы.
Определите ожидаемую прибыль для 6-го года деятельности. Сделайте чертеж
РЕШЕНИЕ
Пусть год=t
Параметры a и b линейной зависимости y=at+b (обозначим прибыль за y ) по методу наименьших квадратов можно найти из системы уравнений
Получаем систему уравнений:
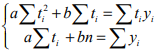
где суммирование ведется по i от 1 до 5. Составим расчетную таблицу:
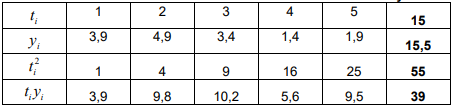
Где последний столбик- это сумма
Получаем систему:
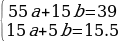
откуда находим a=-0,75 , b=5,35 , то есть получаем функцию y=-0,75t+5,35
Определим ожидаемую прибыль для 6-го года:
y(6)=-0,75*6+5,35=0,85
Построим точки и линию y=-0,75t+5,35 на одной диаграмме:
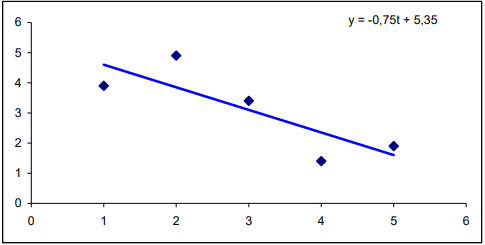
Рисунок 3 - График для примера 2
(Рис. 3)
Глава 3.0.Метод МНК на практике
Метод наименьших квадратов применим ко многим сферам деятельности человека и используется, для теоретического описания экспериментальных данных, как я уже и писал раньше.
За примером обращусь к физике, а конкретному теме оптика. В определенном веществе под действием магнитного поля упорядоченный свет имеет свойство "вращаться", это называется эффектов Фарадея, но основной интерес представляет не физическая составляющая этого, а экспериментальные данные, которые можно получить в ходе выполнения экспериментов. Существует эксперимент, в котором измеряют угол поворота света в зависимости от магнитной индукции. Конечно, все эти темы в курсе школьной физике будут пройдены позже, поэтому я ознакомился с ними лишь для того, чтобы экспериментальные данные привести к зависимости.
Приведу ниже таблицу с данными
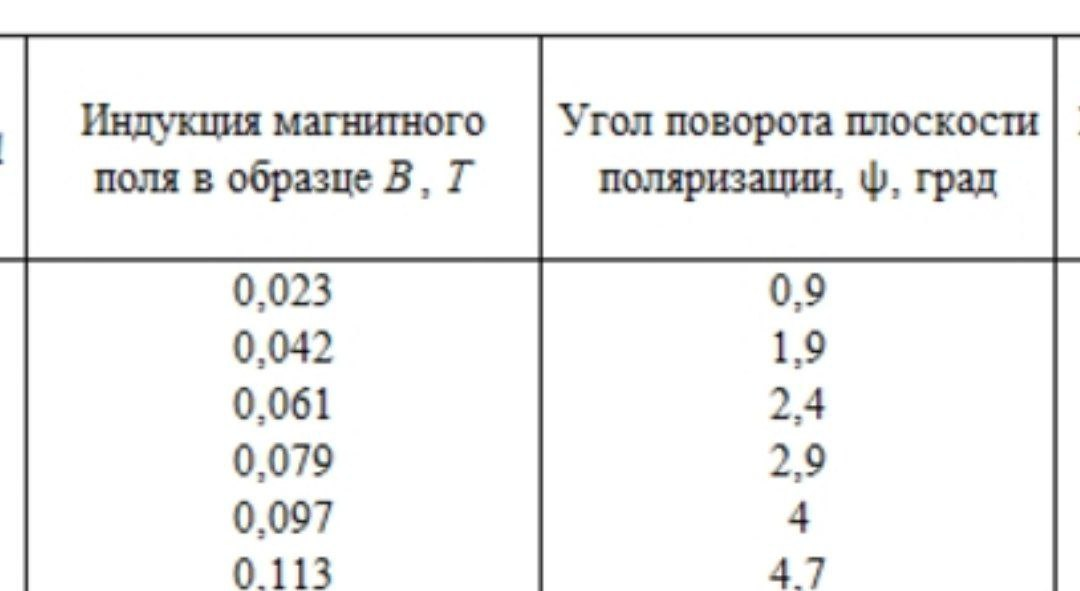
Рисунок 4 - Данные эксперимента
В ходе вычислений получена теоретическая зависимость:
Данные и линейная зависимость представлена ниже:
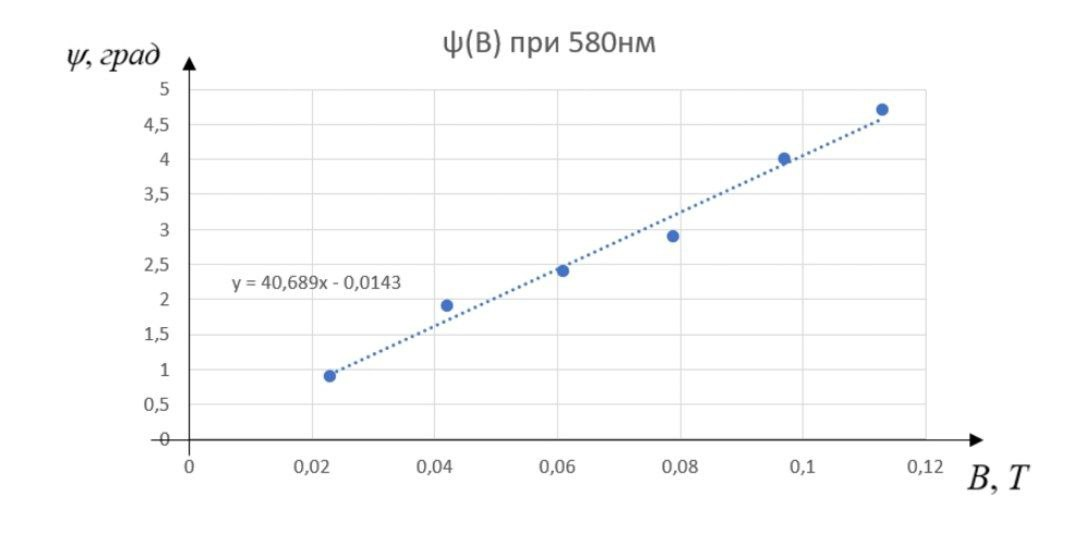
Рисунок 5 - Графическая зависимость
В теории же, где нет погрешностей и всяких других мешающих факторов, зависимость выражается формулой, она тоже линейная
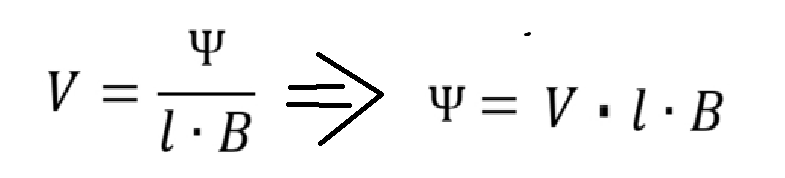
Глава 3.1.Код на PYTHON и его проверка.
Также, я бы хотел показать код на языке программирования PYTHON, используя который вы сможете реализовать МНК для нахождения искомой зависимости.
Ниже представлен пример для экспериментально полученных данных из эксперимента по физике:
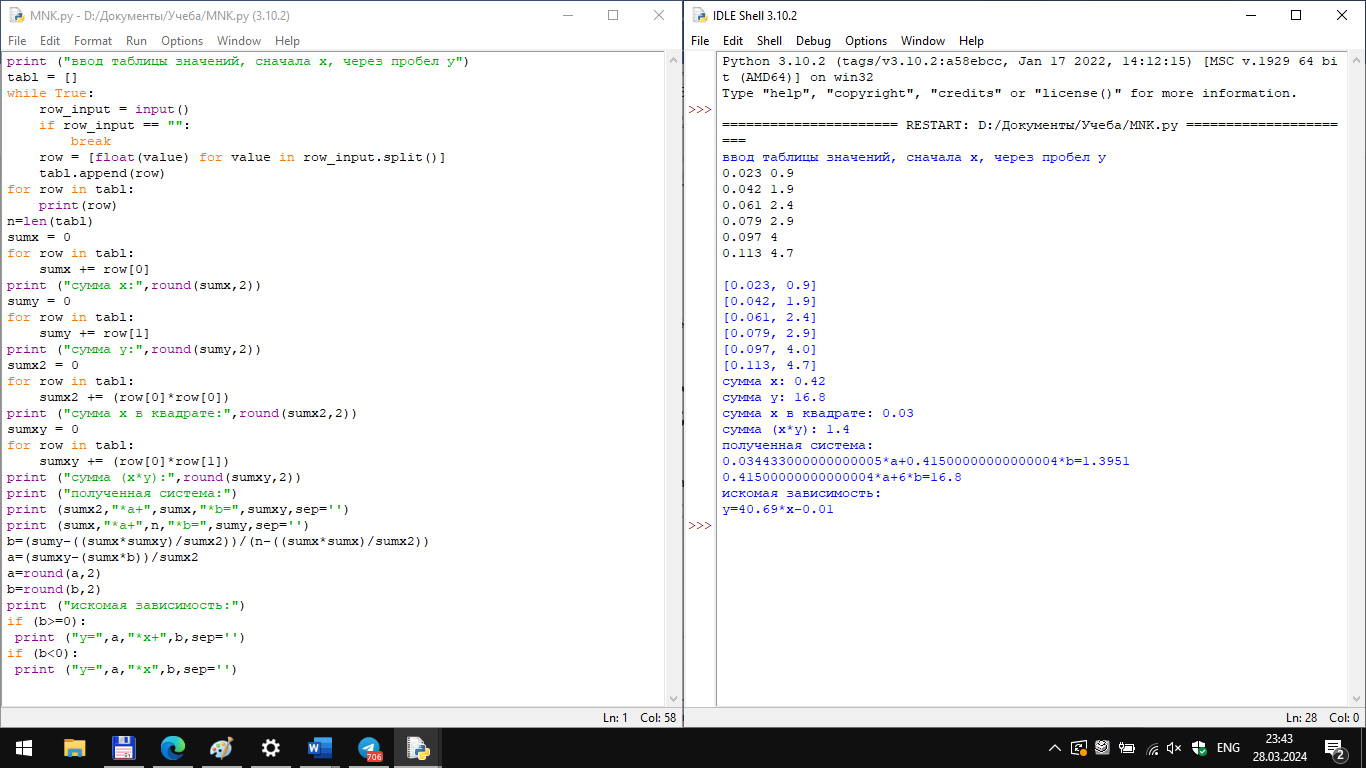
Рисунок 6 – Код и его результат
Этот код представляет собой программу для вычисления уравнения линейной регрессии на основе введенных пользователем данных (таблицы значений иксов и игреков).
-
Сначала программа запрашивает у пользователя ввод таблицы значений, где каждая строка содержит два числа (х и у), разделенных пробелом. Все введенные данные сохраняются в переменной tabl в виде списка списков.
-
Затем программа вычисляет сумму значений x и y, а также сумму квадратов x и произведение x и y.
-
Далее программа выводит полученную систему уравнений вида:
sumx2 * a + sumx * b = sumxy
sumx * a + n * b = sumy
-
Вычисляет коэффициенты a и b по формулам:
b = (sumy - ((sumx * sumxy) / sumx2)) / (n - ((sumx * sumx) / sumx2))
a = (sumxy - (sumx * b)) / sumx2
-
Выводит искомую зависимость в виде уравнения линейной регрессии:
Если коэффициент b неотрицательный, то выводится: y = a * x + b
Если коэффициент b отрицательный, то выводится: y = a * x - b
Заключеиие
-
В ходе выполнения данной исследовательской работы я нашел и выбрал информацию по теме.
2. Понял суть метода наименьших квадратов
3. Изучив различные источники понял, что метод МНК применяется во многих областях
4. Научился применять и решать задачи методом МНК.
5. Узнал, что МНК может использоваться в физике
6. Написал код на PYTHON для решения задач с помощью метода МНК
7. Научился применять и решать задачи методом МНК.
В процессе проведения данного исследования я глубоко погрузился в тему метода наименьших квадратов и осознал его суть. Изучив различные источники информации, я понял, что метод МНК широко применяется в различных областях, таких как статистика, экономика, физика и многие другие.
Путем написания кода на Python для решения задач с использованием метода наименьших квадратов, я освоил этот метод и научился применять его для аппроксимации данных и построения уравнения линейной регрессии.
Особенно интересным для меня было узнать, что метод наименьших квадратов может быть успешно применен в физике. Этот метод позволяет анализировать экспериментальные данные, устанавливать зависимости между переменными и делать прогнозы.
В результате проведенной работы я пришел к выводу, что гипотеза, выдвинутая мной, подтвердилась. Результаты, полученные при выполнении лабораторной работы по физике с использованием метода наименьших квадратов, оказались близкими к реальным значениям, что свидетельствует о точности и эффективности данного метода.
Используйте и вы метод наименьших квадратов в вашей сфере деятельности. Этот метод может стать мощным инструментом для анализа данных, построения моделей и принятия обоснованных решений. Погрузитесь в мир метода наименьших квадратов и откройте новые возможности для исследований и анализа данных.
Интернет ресурсы
https://www.matburo.ru/ex_ms.php?p1=msmnk
https://ru.wikipedia.org/wiki/Метод_наименьших_квадратов
https://books.econ.msu.ru/Introduction-to-Econometrics/chap02/2.2/
https://help.fsight.ru/ru/mergedProjects/lib/01_regression_models/uimodelling_linearregr_lsm.htm
https://www.youtube.com/watch?v=UcwI7tY7bss





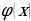
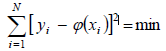
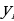 и
и 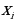 – экспериментальные значения переменных в i-том опыте, N – число опытов,
– экспериментальные значения переменных в i-том опыте, N – число опытов, 
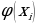 , а
, а