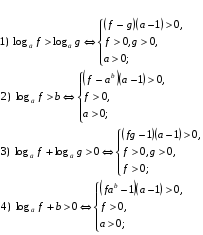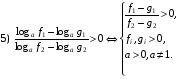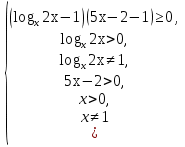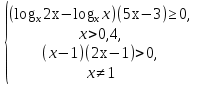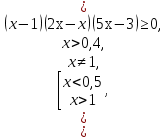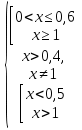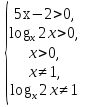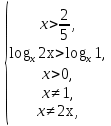Метод рационализации в решении неравенств

Факльтатив «Подготовка к ЕГЭ по математике 11 класс»

Тема; метод рационализации в решении неравенств

цель работы – предложить метод решения сложных неравенств (неравенства, содержащие логарифмические, показательные, иррациональные выражения и выражения с модулями) путем замены множителей.

Содержание

1. Метод рационализации при решении неравенств, содержащих логарифмические функции.

2. Метод рационализации при решении неравенств, содержащих иррациональные выражения.

3. .Метод рационализации при решении неравенств, содержащих модули.

4. Метод рационализации при решении неравенств, содержащих показательные функции.

Ход урока
Самым легким способом решения неравенств является способ решения рациональных неравенств методом интервалов, но не все неравенства имеют структуру, которая позволяет решать их этим методом. Поэтому Идея этого метода заключается в том, что неравенства повышенной сложности сводятся к решению рациональных неравенств. Оказывается, достаточно широкий класс неравенств подобную попытку допускает. Решение неравенства – это объединение конечного числа непересекающихся промежутков. Их легко задать одним рациональным неравенством, что во многих ситуациях позволяет быстрее двигаться к ответу, а иногда получать более эффективные схемы решения типовых неравенств.

Метод рационализации при решении неравенств, содержащих логарифмические функции.

Разность логарифмов по одному и тому же основанию всегда по знаку совпадает с произведением разности чисел этих логарифмов на отклонение от единицы. Другими словами выражение вида (log_af – log_ag) имеет тот же знак (в области существования логарифмов) что и выражение (f-g)(α-1)

Выделим некоторые выражения и соответствующие рационализирующие выражения, позволяющие исключительно эффективно решать многие логарифмические неравенства, которые можно отнести к разряду повышенной сложности.

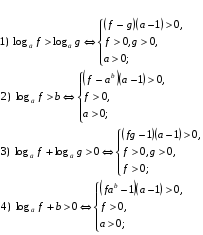
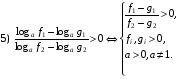
Примеры решения логарифмических неравенств методом рационализации.

Приведем сравнение решения неравенства традиционным методом и методом рационализации:

№1. Решить неравенство:

(метод рационализации)

Решение:

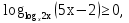
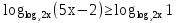
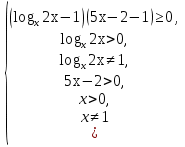
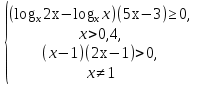
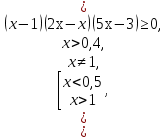
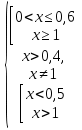
Отв

( традиционный метод)

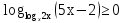
Решение:

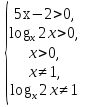
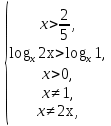
1) ОДЗ: 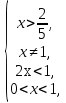или; 

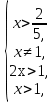
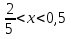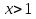
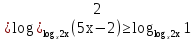
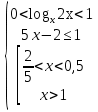
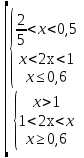
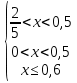
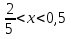1. б)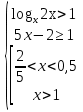 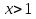Ответ:

№2. Решить неравенство:

Решение: 

№3.Решить неравенство:

Решение: , 

Ответ: (

№4. Решить неравенство 

Решение:

,,

Ответ: (-1,5;-1)(-1;0)(0;3)

№5. Решить неравенство 

Решение:

,Ответ: (-0,5;

№6. Решить неравенство Решение:

Ответ: (-1;0)№7. Решить неравенство :.Решение: , ,

Ответ: 

№8. Решить неравенство 

Решение:

,

Ответ: 

№9. Решить неравенство 

Решение:

а)

0,5, 1,6

Имеем

следовательно ;;

б) если x-3=1, x=2- не является решением (при x=2 ) .

Ответ:;;

№10. Решить неравенство

Решение:

Ответ: 

№11. Решить неравенство 

Решение:

1 Ответ: 1

№12. Решить неравенство 

Решение:

) 

; 0 Ответ: ; 0

№13. (Применение метода рационализации при решении неравенств с параметрами)

Решить неравенство.

Рассмотрим два случая.

1)Пусть . Тогда получим, что  и  следовательно, для любых x, что не удовлетворяет условию задачи.

2) Пусть теперь  . В этом случае  и, для того чтобы неравенство было верно для любых x , необходимо и достаточно, чтобы выполнялось условие .

Получим систему:Ответ: (

Метод рационализации при решении неравенств, содержащих иррациональные выражения.

При решении неравенств, содержащих иррациональные выражения, используем следующее правило -(на области определения)

№1.Решите неравенство:

Решение.
 

-7Ответ: -71

№2.Решите неравенство

Решение: 
Ответ: 

№3Решите неравенство

Решение:
Ответ: 0

№4Решить неравенство:

Решение: 
Ответ: 

№5 Решить неравенство:

Решение:
Ответ: 

№6.Решить неравенство:

Решение:

Ответ:

Метод рационализации при решении неравенств , содержащих модули.

Опорная информация, позволяющая указать удобные замены, заключается в двух основных свойствах модуля:

│m│² = m² и │m│≥0 для всех m,

а также в монотонном возрастании на множестве неотрицательных чисел функцииy=t².

Приведем типы замен:

,

№1.

: 

(,

(10x+32)(2(10x+32)2x(x+5) ,

-5 

Ответ: -5

Для решения дробных неравенств, содержащих модули удобно использовать следующее правило:
 

Решение:

-6

Ответ: -6

№3.Решить неравенство:

Решение:

-9

Ответ: -9

№4.Решить неравенство: 

Решение:

x , 2 4

Ответ: x , 2 4

№5.Решить неравенство: 

Решение:

Ответ: x

№6. Решить неравенство:

Решение:

x, 3Ответ: x, 3

№7. Решить неравенство:

-13 Ответ: -13
Решить неравенство:

Ответ: 

Метод рационализации при решении неравенств, содержащих показательные функции

Можно установить, что разность степеней по одному и тому же основанию всегда по знаку совпадает с произведением разности показателей этих степеней на отклонение основания степени от единицы. Другими словами, выражение вида  имеет тот же знак, что и выражение

(f –g)(а – 1) при а 0 (если а=1, то выражения равны нулю)

№1.Решить неравенство:

Решение:

;

Ответ: 

№2.Решить неравенство:

Решение:

Ответ: 

№3.Решить неравенство:

Решение:

Ответ: 

№4.Решить неравенство:

Решение:

;

Ответ: 

№5.Решить неравенство:

Решение:. На множестве 

исходное неравенство равносильно 

x(2x+1)(3x-7)

Получ  Ответ: 

№6.Решить неравенство 

Решение: Область определения неравенства: 

Применим метод рационализации неравенства:

(x+1)x(x-1) Ответ: 

№7.Решить неравенство

Решение:

Первый множитель в числителе заменяем на , второй на  , третий на, четвертый на

, пятый на .

Первый множитель в знаменателе заменяем на, а второй на.

Получаем в области допустимых значений рациональное неравенство, равносильное исходному:

Область существования всех множителей в исходном неравенстве представляет собой два промежутка: . В этой области множители знакопостоянны, и поэтому их знаменяем соотвестственно на (-1) и 1.

Знакопостоянны и трехчлены , поэтому их заменяем также, соответственно на (-1) и 1.

Решая последнее стандартное рациональное неравенство в указанной области существования всех множителей исходного неравенства, получаем ответ:

.