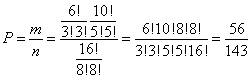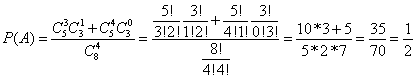ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА
Тема: «Основные понятия и методы теории вероятностей»
Специальность: 31.02.01 Лечебное дело Курс: 1
Купино
2019
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2019 г
Пояснительная записка
Методическое пособие предназначено для самостоятельного изучения теоретических и практических знаний по теме Основные понятия и методы теории вероятностей, повторения понятий: вероятности, формулы вероятности, теорем сложения и умножения вероятностей, определений достоверного, невозможного, несовместных, противоположных, равновозможных событий для подготовки к занятиям по этой теме.
Данное пособие рекомендовано для студентов первого курса специальности 31.02.01 Лечебное дело. Пособие содержит определения основных понятий по теме Основные понятия и методы теории вероятностей, вопросы для самопроверки, образцы решения задач и задачи для самостоятельного решения.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Основные понятия и методы теории вероятностей
События (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.
Достоверным называют событие, ĸᴏᴛᴏᴩᴏᴇ обязательно произойдет, в случае если будет осуществлена определенная совокупность условий S.
К примеру, в случае если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие вода в сосуде находится в жидком состоянии есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S.
Невозможным называют событие, ĸᴏᴛᴏᴩᴏᴇ заведомо не произойдет, в случае если будет осуществлена совокупность условий S. К примеру, событие ʼʼвода в сосуде находится в твердом состояние заведомо не произойдет, в случае если будет осуществлена совокупность условий предыдущего примера.
Случайным называют событие, ĸᴏᴛᴏᴩᴏᴇ при осуществлении совокупности условий S может либо произойти, либо не произойти. К примеру, в случае если брошена монета͵ то она может упасть так, что сверху будет либо герб, либо надпись. По этой причине событие ʼʼпри бросании монеты выпал ʼʼгербʼʼ — случайное. Каждое случайное событие, в частности выпадение ʼʼгербаʼʼ, есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета͵ форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. По этой причине теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, — она просто не в силах это сделать.
По-иному обстоит дело, в случае если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
Т.о., предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Методы теории вероятностей широко применяются в различных отраслях естествознания и техники. Теория вероятностей служит также для обоснования математической и прикладной статистики.
Виды случайных событий. События называют несовместными, в случае если появление одного из них исключает появление других событий в одном и том же испытании.
Пример.
Брошена монета. Появление ʼʼгербаʼʼ исключает появление надписи. События ʼʼпоявился гербʼʼ и ʼʼпоявилась надписьʼʼ — несовместные.
Несколько событий образуют полную группу, в случае если в результате испытания появится хотя бы одно из них. В частности, в случае если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. Этот частный случай представляет для нас наибольший интерес, поскольку используется далее.
Пример 2. Приобретены два билета денежно-вещевой лотереи. Обязательно произойдет одно и только одно из следующих событий: ʼʼвыигрыш выпал на первый билет и не выпал на второйʼʼ, ʼʼвыигрыш не выпал на первый билет и выпал на второйʼʼ, ʼʼвыигрыш выпал на оба билетаʼʼ, ʼʼна оба билета выигрыш не выпалʼʼ. Эти события образуют полную группу попарно несовместных событий.
Пример 3. Стрелок произвел выстрел по цели. Обязательно произойдет одно, из следующих двух событий: попадание, промах. Эти два несовместных события образуют полную группу.
События называют равновозможными, в случае если есть основания считать, что ни одно из них не является более возможным, чем другое.
Пример 4. Появление ʼʼгербаʼʼ и появление надписи при бросании монеты —равновозможные события. Действительно, предполагается, что монета изготовлена из однородного материала, имеет правильную цилиндрическую форму и наличие чеканки не оказывает влияния на выпадение какой-либо стороны монеты.
События обозначаются прописными буквами латинского алфавита: А, В, С,.. А1, А2..
Противоположными называют 2 единственно возможных соб-я, образующих полную группу. В случае если одно из двух противоположных событий обозначено через А, то др. обозначается А`.
Пример 5. Попадание и промах при выстреле по цели – противоположные события.
Классическое определение вероятности случайного события
Под вероятностью случайного события в математике понимают меру возможности осуществления данного события в конкретных условиях эксперимента (испытания).
Рассмотрим некоторую конечную полную группу равновоз-можных элементарных событий (исходов) В,, В2, ..., Вп, т. е. совокупность всех единственно возможных, несовместных и вместе с тем равновозможных результатов некоторого испытания, причем пусть интересующее нас случайное событие А осуществляется тогда и только тогда, когда наступают некоторые из элементарных событий указанной полной группы. Пусть таких событий, благоприятствующих для события А, насчитывается т(естественно, тТогда вероятность события А определяют следующим образом:
Определение. Вероятностью Р(А) случайного события А называется отношение количества т элементарных событий, благо-приятствующих событию А, к общему количеству элементарных событий п:
P*(A)=m/n
Поскольку в общем случае 0 т то из этого определения, называемого классическим определением вероятности случайного события, следует, что вероятность произвольного случайного события принадлежит отрезку [0,1], т.е.
0≤ Р(А)≤1
Пример 1. Найти вероятность того, что при извлечении наугад одного шара из корзины, в которой находятся 2 белых, 3 зеленых и 5 красных шаров, извлеченный шар окажется зеленым.
Решение. Поскольку общее количество элементарных событий (исходов) для данного испытания образует полную группу из n=10 равновозможных событий (по общему количеству шаров в корзине), из которых только т = 3 элементарных события (по количеству зеленых шаров) являются благоприятствующими для интересующего нас события (обозначим это событие через А),по формуле (8.1) получим:
Р(А)=3/10
Основные свойства вероятности случайного события
1. Вероятность невозможного события равна нулю. Действительно, поскольку количество т элементарных событий, благоприятствующих невозможному событию А, равно нулю, получаем:
Р(А) = 0/п=0
2. Вероятность достоверного события равна единице. Действительно, поскольку количество т элементарных событий, благоприятствующих достоверному событию А, равно общему количеству п этих элементарных событий, получаем:
Р(А) = п/ п=1
1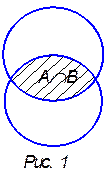 . Элементы и множества. Операции над множествами и их свойства.
. Элементы и множества. Операции над множествами и их свойства.
1. Пересечением множеств А и В называется множество, состоящее из элементов, которые принадлежат множествам А и В одновременно.
Пересечение множеств А и В обозначают: А Ç В.
Если представить множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью (рис. 1).
В том случае, когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто и пишут: А Ç В = Æ.
А Ç Æ = Æ.
Операция, при помощи которой находят пересечение множеств, называется также пересечением.
Пример.
1) А ={1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А Ç В = {4, 5}
2) Пересечением множества прямоугольников и множества ромбов является множество квадратов.
3) Пересечением множества чётных чисел и множества нечётных чисел пусто.
2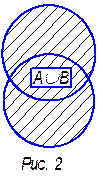 . Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В.
. Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В.
Объединение множеств А и В обозначают: А È В.
А È В = {х| хÎА или хÎВ}
Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью (рис. 2).
Если ВÌ А, то А È В = А.
А È Æ = А.
Операция, при помощи которой находят объединение множеств, называется также объединением.
Пример.
1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А È В = {1, 2, 3, 4, 5, 6, 7}
2) Объединение множества положительных чётных чисел и множества положительных нечётных чисел является множество натуральных чисел.
Если в выражении есть Ç и È множеств, но нет скобок, то сначала выполняют Ç.
Операции пересечения и объединения множеств обладают свойствами:
1° Коммутативность пересечения
"А, В А Ç В = В Ç А
2° Коммутативность объединения
"А, В А È В = В È А
3º Ассоциативность пересечения
"А, В, С (А Ç В) Ç С = А Ç (В Ç С)
4º Ассоциативность объединения
"А, В, С (А È В) È С = А È (В È С)
5º Пересечение дистрибутивно относительно объединения
"А, В, С А Ç (В È С) = (А Ç В) È (А Ç С)
6º Объединение дистрибутивно относительно пересечения
"А, В, С А È (В Ç С) = (А È В) Ç (А È С)
7º "А А Ç А = А
8º "А А È А = А
3. Разностью множеств А и В называется множество, элементы которого принадлежат множеству А и не принадлежат множеству В.
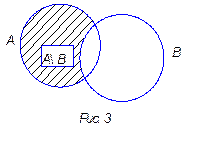 Обозначают А \ В; А – В.
Обозначают А \ В; А – В.
А \ В = { х| хÎА и хÏВ }
Если представить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью (рис. 3).
Операция, при помощи которой находят разность множеств, называется вычитанием.
Пример.
1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}
А \ В = {1, 2, 3}
2) Разностью множества чётных чисел и множества целых чисел является пустое множество.
4. Симметрической разностью множеств А и В называется множество, состоящее из элементов, принадлежащих только множеству А или только множеству В.
С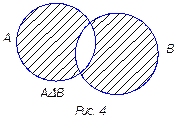 имметрическую разность множеств А и В обозначают: А х В; А – В.
имметрическую разность множеств А и В обозначают: А х В; А – В.
А х В = { х| хÎА, хÏВ или хÏА, хÎВ}
Если представить множества А и В при помощи кругов Эйлера, то симметрическая разность данных множеств изобразится заштрихованной областью (рис. 4).
А х В = (А \ В) È (В\ А)
А х В = (А È В) \ (А Ç В)
5. Универсальным множеством U (основным множеством) называется множество, для которого все множества, рассматриваемые в данный момент, являются подмножествами.
Универсальное множество часто изображают прямоугольником.
Например, для N универсальным считается множество Z.
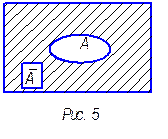
Дополнением множества А называется разность между универсальным множеством и множеством А.
Дополнение множества А обозначают 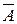 .
.
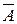 = U \ A = {хÏА}
= U \ A = {хÏА}
При помощи кругов Эйлера дополнение изображается рис. 5.
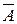 È А = U
È А = U 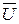 = Æ
= Æ
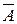 Ç А = Æ = U
Ç А = Æ = U
Пример.
1) А = {2k}; U = Z ® 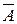 = Z \A = {2k+1}.
= Z \A = {2k+1}.
Операции разности и дополнения множеств обладают свойствами:
9º Разность антидистрибутивна относительно пересечения. "А, В, С
А \ (В Ç С) = (А \ B) È (A \ C)
10º Разность антидистрибутивна относительно объединения. "А, В, С
А \ (В È С) = (А \ B) Ç (A \ C)
11º (частный сл. 9º) Дополнение пересечения А и В равно объединению дополнений А и В.
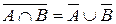
12º (частный сл. 10º) Дополнение объединения А и В равно пересечению дополнений А и В.
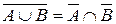
Вопросы для самопроверки
Сформулируйте определение случайного события (ТЗ 37)
Сформулируйте определение достоверного события (ТЗ 38)
Сформулируйте определение невозможного события (ТЗ 39)
Сформулируйте определение равновозможных событий (ТЗ 40)
Сформулируйте определение несовместных событий (ТЗ 41)
Сформулируйте определение противоположных событий (ТЗ 42)
Сформулируйте определение вероятности случайного события (ТЗ 43)
Задачи для самостоятельного решения
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 139
Текст задания: Для проведения лабораторных работ группа студентов, в которой 10 студентов и 6 студенток, произвольным образом делится на 2 равные подгруппы. Найти вероятность того, что в каждой подгруппе окажется по одинаковому числу студенток.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 140
Текст задания: На книжной полке 8 журналов, из которых 5 в переплете. Наудачу взяты 4 журнала. Найти вероятность того, что среди них окажется не менее трех в переплете.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 141
Текст задания: В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Используя классическое определение теории вероятности определить, какова вероятность того, что обе детали окажутся бракованными.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 142
Текст задания: В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым)?
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 143
Текст задания: В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 144
Текст задания: Имеется три одинаковых по виду ящика. В первом ящике находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26 черных шаров. Из выбранного наугад ящика вынули белый шар. Используя формулу Байеса вычислить вероятность того, что белый шар вынут из первого ящика.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 145
Текст задания: На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей зависимых событий определить вероятность того, что обе детали окажутся стандартными.
Критерии оценивания задач:
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 139
Текст задания: Для проведения лабораторных работ группа студентов, в которой 10 студентов и 6 студенток, произвольным образом делится на 2 равные подгруппы. Найти вероятность того, что в каждой подгруппе окажется по одинаковому числу студенток.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Число всевозможных элементарных исходов – количество способов разделить 16 студентов на 2 равные группы (то есть выбрать из 16 человек 8) 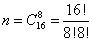
Число благоприятствующих исходов – число исходов, при котором в каждой группе будет по 3 студентки 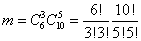 (Из 6 студенток нужно выбрать 3 -
(Из 6 студенток нужно выбрать 3 - 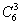 И из 10 студентов 5 -
И из 10 студентов 5 - 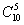 – по правилу умножения вероятностей независимых событий
– по правилу умножения вероятностей независимых событий 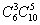 )
)
Тогда, по классическому определению вероятности
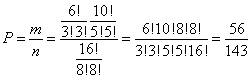
Ответ: 56/143
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 140
Текст задания: На книжной полке 8 журналов, из которых 5 в переплете. Наудачу взяты 4 журнала. Найти вероятность того, что среди них окажется не менее трех в переплете.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Элементарными исходами здесь являются наборы, включающие 4 журнала. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов 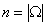 равно числу способов выбрать 4 журнала из 8, т. е. числу сочетаний
равно числу способов выбрать 4 журнала из 8, т. е. числу сочетаний 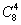 . Число благоприятствующих исходов
. Число благоприятствующих исходов 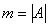 равно числу способов выбора 3 или 4 журнала в переплёте из имеющихся 4, т. е.
равно числу способов выбора 3 или 4 журнала в переплёте из имеющихся 4, т. е. 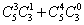
Тогда искомая вероятность
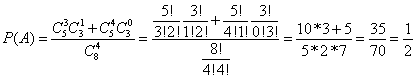
Ответ: 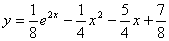

Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 141
Текст задания: В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Используя классическое определение теории вероятности определить, какова вероятность того, что обе детали окажутся бракованными. .
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Число N всех равновероятных исходов испытания равно числу способов, которыми можно из 23 деталей вынуть две, т.е. числу сочетаний из 23 элементов по 2:
Число благоприятных исходов
Cледовательно, искомая вероятность
 Ответ:
Ответ:  0,178
0,178
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 142
Текст задания: В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым)?
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Всего в ящике лежит N=4+10+8+9=31 шар.
Вероятность вытащить красный шар
Вероятность вытащить зеленый шар
Вероятность вытащить коричневый шар
Т.к. эти три события несовместны, то пользуясь теоремой сложения вероятностей определим вероятность того, что шар окажется цветным (не белым)
Ответ: 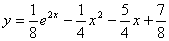 0,871
0,871
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 143
Текст задания: В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Вероятность вытащить знакомый вопрос p=0.75, незнакомый q=1-p=1-0.75=0.25
Пусть H1 - гипотеза, что студент не знает ни одного из 2-х вопросов.
Вероятность этой гипотезы:
Искомая вероятность соответственно равна:
 Ответ:
Ответ: 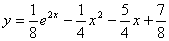 0,9375
0,9375
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 144
Текст задания: Имеется три одинаковых по виду ящика. В первом ящике находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26 черных шаров. Из выбранного наугад ящика вынули белый шар. Используя формулу Байеса вычислить вероятность того, что белый шар вынут из первого ящика.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Пусть A - событие, состоящее в том, что взятый шар окажется белым, а H1 и H2 - гипотезы, что он был взят из 1-го и 2-го ящика. (Третий ящик рассматривать не будем, т.к. там только черные шары, а из условий известно, что вынут именно белый шар.)
Вероятности указанных гипотез соответственно равны:
, здесь N=26+15+11=52 - количество шаров в 1-м и 2-м ящиках
Из условия задачи следует, что:
Найдем PA(H1), т.е. вероятность того, что вынутый белый шар был взят из 1-го ящика.
Ответ: 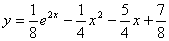 0,75
0,75
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 145
Текст задания: На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей зависимых событий определить вероятность того, что обе детали окажутся стандартными.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Извлечение двух деталей равносильно последовательному их извлечению. Обозначим через A - появление стандартной детали при первом извлечении, а через B - при втором. Событие, состоящее в извлечении двух стандартных деталей, является совмещением событий А и B.
Пользуясь теоремой умножения вероятностей имеем:
 , где
, где 
Поскольку после того, как была вынута первая стандартная деталь на складе осталось 25 деталей, из которых 12 стандартных, то
 , тогда
, тогда
Ответ: 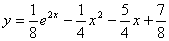 0,24
0,24
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.






 . Элементы и множества. Операции над множествами и их свойства.
. Элементы и множества. Операции над множествами и их свойства. . Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В.
. Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В. Обозначают А \ В; А – В.
Обозначают А \ В; А – В.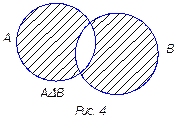 имметрическую разность множеств А и В обозначают: А х В; А – В.
имметрическую разность множеств А и В обозначают: А х В; А – В.