Управление образования и молодежной политики
администрации Городецкого района
Методическая разработка
раздела учебной программы.
Тема: «Прогрессии».
ВЫПОЛНИЛ:
Должность: учитель
ФИО: Лебедева Галина Борисовна
Образование: высшее
Стаж работы в данной должности
25 лет
Консультант: Быстрова Галина Ивановна
2011 год
Содержание.
-
Пояснительная записка--------------------------------------------------------------------------------3
-
Цели и задачи раздела---------------------------------------------------------------------------------5
-
Ожидаемые результаты освоения раздела программы-----------------------------------------6
-
Поурочное планирование по разделу--------------------------------------------------------------7
-
Психолого-педагогическое объяснение специфики восприятия и освоение
учебного материала учащимися в соответствии с возрастными особенностями---------9
-
Обоснование образовательных технологий, методов,
форм организации деятельности учащихся-----------------------------------------------------12
-
Система знаний и система деятельности---------------------------------------------------------21
-
Разработка урока---------------------------------------------------------------------------------------22
-
Список литературы------------------------------------------------------------------------------------38
Приложения.
.
1. Пояснительная записка.
«… Главная задача современной школы – это раскрытие способностей каждого ученика, воспитание личности , готовой к жизни в высокотехнологичном конкурентном мире…»
(Из Послания Президента РФ Д.А. Медведева Федеральному собранию РФ от 12.11.2009)
Научными основаниями современной концепции образования выступают классические и современные педагогические и психологические подходы – гуманистический, развивающий, индивидуальный, компетентностный, деятельный, личностно-ориентированный. Одной из ведущих целей образования является повышение качества обучения и формирование личности, готовой к самореализации и выполнению социально-востребованной деятельности и общения.
Образование должно выявлять и развивать индивидуальные способности и склонности учащихся. В этом случае задача школы – создание условий, благоприятных для возможно более полного развития и раскрытия индивидуальности. Школа должна научить детей самостоятельно добывать информацию и уметь ею пользоваться – это неотъемлемое качество культурного человека в наше время.
Математика есть часть общего образования. Она призвана содействовать гармоническому развитию личности, формировать ее интеллект и дать опору в будущей профессиональной деятельности. Особая цель математического образования – развитие речи на уроках математики. В наше прагматичное время культурный человек должен уметь излагать свои мысли четко, кратко, раскладывая «по полочкам», умея за ограниченное время сформулировать главное, отсечь несущественное.
Математика как общеобразовательный предмет оказывает большое влияние на умственное развитие учащихся.
Математику уже затем учить надо, что она ум в порядок приводит.
(М. В. Ломоносов)
Она является фундаментальным мировоззрением, формирует основы логического мышления, создает базу для изучения целого цикла учебных предметов, знания математики необходимы для многочисленных специалистов.
Как учебный предмет математика изучается в систематическом виде с 1 по 11 класс, но на последнем этапе обучения (9-11 класс) систематизируются все полученные знания, обобщаются, создается установка на дальнейшую деятельность, для дальнейшего обучения в высших учебных заведениях.
В девятом классе изучение алгебры завершается итоговой аттестацией по предмету, поэтому интерес к математике у учащихся возрастает, связан с подготовкой к предстоящему экзамену, в большинстве своем ученики осознают уровень своих знаний и проблемы в них, поэтому желают систематизировать и обобщить изученный материал курса алгебры.
На изучение алгебры в 9 классе отводится 3 часа, из них на обобщающее повторение приходится не более 10-15 уроков в конце учебного года, что чрезвычайно мало. Исходя из вышесказанного, мне хотелось показать в своей работе, как сэкономить 2 – 3 урока при изучении темы “ Прогрессии” и присоединить эти уроки к итоговому повторению.
Методическая разработка по разделу «Прогрессии» составлена на основе федерального компонента Государственного стандарта среднего (полного) общего образования.
Статус работы.
Методическая разработка по данному разделу выполняет две основные функции:
-
Информационно-методическую (дает представление о целях, содержании, общей методике обучения, воспитания и развития учащихся средствами данного учебного раздела);
-
Организационно-планирующую (предусматривает структурирование учебного материала по данному разделу, определение его количественных и качественных характеристик).
-3-
Структура работы.
Методическая разработка содержит несколько разделов: пояснительную записку, цели и
задачи раздела, ожидаемые результаты освоения раздела, поурочное планирование, психолого-педагогическое объяснение специфики восприятия и освоение учебного материала учащимися в соответствии с возрастными особенностями, обоснование образовательных технологий,
методов и форм организации деятельности учащихся, разработку урока.
Общая характеристика учебного раздела.
При изучении раздела «Прогрессии» продолжаются и получают развитие содержательные линии: «Алгебра», «Функции», «Уравнения и системы уравнений», «Математический язык. Математическая модель». В рамках указанных содержательных линий решаются следующие задачи:
-
Изучение новых видов математических моделей, связанных с прогрессиями; совершенствование практических навыков и вычислительной культуры; совершенствование алгебраического аппарата и его применение к решению математических задач;
-
Пополнение класса изучаемых функций (функция натурального аргумента или числовая последовательность), способов ее задания; иллюстрация широты применения числовых последовательностей для описания реальных жизненных ситуаций;
-
Совершенствование интеллектуальных и речевых умений путем обогащения математического языка.
Место раздела в учебном плане.
Обучение ведется по учебному комплекту А. Г. Мордковича для изучения курса алгебры в
7 - 9 классах общеобразовательной школе. Согласно поурочному планированию учебного материала тема «Прогрессии» вводится после числовых функций. В данном курсе приоритет отдается функциональной линии, поэтому и последовательности подаются в этом же ключе. Это функция, но несколько отличающаяся от того к чему привыкли ученики; это функция натурального аргумента. На тему « Прогрессии» отводится 16 часов.
Понятие последовательностей находит широкое применение и в дальнейшем: при определении степени с действительным показателем, при введении понятия определенного интеграла, а также в межпредметных связях (физика, экономика).
Общеучебные умения, навыки и способы деятельности.
В ходе освоения содержания раздела «Прогрессии» учащиеся продолжают овладевать разнообразными способами деятельности, приобретают и совершенствуют опыт:
-
Обобщения, анализа, определения причинно-следственных связей, выделения учебной задачи;
-
Развития логической (смысловой) памяти, категориального системного мышления, способности к рефлексии;
-
Формирования навыков межличностного общения;
-
Ориентирования на цели, выходящие за пределы сегодняшнего дня (в том числе профориентация, самоактуализация личности и жизненное самоопределение);
-
Формирования социального интеллекта (умение брать ответственность за свои действия и поступки на себя).
Результаты обучения.
Свободное оперирование учащимися знаниями по данному разделу на основе овладения понятиями числовой последовательности и ее членов; способов заданий последовательностей; их разновидностей (арифметическая и геометрическая); формулами для расчета их характеристик.
-4-
2. Цели и задачи раздела «Прогрессии».
Формирование понятия числовой последовательности и ее членов, свойств и графика функции натурального аргумента (числовой последовательности) и способов ее задания; навыков и умений при нахождении членов числовой последовательности, при распознавании разновидностей числовых последовательностей (арифметическая и геометрическая прогрессии); навыков решения задач, связанных с арифметической и геометрической прогрессией.
Развитие логического мышления, внимания; интеллектуальных мыслительных операций: анализа, обобщения, аналогии, классификации и др.; творческих способностей, что способствует дальнейшему обучению и будущей профессиональной деятельности.
Овладение устным и письменным математическим языком; навыком общения ( монолог, диалог, дискуссия, умение слушать, задавать вопросы); методами взаимообучения (работа в группах, в парах, техника выступления, взаимооценка, самооценка), что поможет самореализации личности и ее творческих возможностей.
Воспитание умения самостоятельно добывать знания не только работая с учебником, но и пользуясь справочниками, таблицами и другой дополнительной литературой; самостоятельности как черты личности, что в дальнейшем позволит самостоятельно решать различные жизненные задачи.
Задачи:
Обучающие: сформировать у учащихся понятие новой математической модели – числовой последовательности (функции натурального аргумента) , способов ее задания (аналитический, словесный, рекуррентный) и ее разновидностей (арифметическая и геометрическая прогрессия); учащиеся овладевают новыми терминами математического языка: числовые последовательности, монотонная (возрастающая, убывающая) последовательность, арифметическая прогрессия, разность арифметической прогрессии, геометрическая прогрессия, знаменатель геометрической прогрессии, символическим языком (y1,y2 …
yn или (yn), ÷, Sn); учащиеся вырабатывают формально- оперативные алгебраические умения и учиться применять их к решению математических и нематематических задач.
Развивающие: учащиеся выявляют особенности новой математической модели (числовой последовательности), формулируют и обосновывают свойства арифметической и геометрической прогрессии, сопоставляют и обобщают знания о них, оценивают практическое применение новой математической модели в реальной жизненной ситуации.
Воспитывающие: учащиеся понимают и убеждаются в том, что числовая последовательность важное понятие в математике, оно используется и в дальнейшем: при определении степени с действительным показателем, при введении понятия определенного интеграла и находит практическое применение в физике для описания закона радиоактивного распада и в экономике.
-5-
3. Ожидаемые результаты освоения раздела программы.
Требования к уровню подготовки выпускников основной школы.
В результате изучения раздела «Прогрессии» ученик должен знать и понимать:
-
Существо понятия математического доказательства (характеристические свойства прогрессий); приводить примеры доказательств;
-
Существо понятия алгоритма; приводить примеры алгоритмов (например, решения задач на нахождение п-го члена прогрессий);
-
Как используются формулы п-го члена прогрессий, суммы п первых членов прогрессий, уравнения и системы уравнений для решения математических и практических задач;
-
Как функция натурального аргумента может описывать реальные зависимости; приводить примеры такого описания;
-
Как потребности практики привели математическую науку к необходимости расширения понятия числа как способа построения нового математического аппарата для решения практических задач и внутренних задач математики;
-
Смысл идеализации, позволяющей решать задачи реальной действительности математическими методами; примеры ошибок, возникающих при идеализации.
В результате изучения раздела «Прогрессии» ученик должен уметь:
вычисления и преобразования:
-
Составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
-
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, производить отбор решений, исходя из формулировки задач;
-
Распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
функции:
-
Задавать функцию натурального аргумента различными способами (аналитический, словесный, рекуррентный);
-
Изображать график функции натурального аргумента, описывать свойства этой функции;
уравнения и неравенства:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
Выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужных формул в справочных материалах;
-
Моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
Интерпретации графиков реальных зависимостей между величинами;
-
Выстраивания аргументации в форме монолога и диалога;
-
Распознавания логически некорректных рассуждений;
-
Записи математических утверждений, доказательств;
-
Решения практических задач в повседневной и профессиональной деятельности с использованием знаний об арифметической и геометрической прогрессиях.
-6-
4. Поурочное планирование по разделу «Прогрессии».
Предлагаемые программы (примерные и авторские) по алгебре за 2010 год составлены в соответствии с требованиями федерального компонента Государственного образовательного стандарта среднего (полного) общего образования по математике. Они позволяют получить полное представление о целях и содержании обучения алгебры в 7 – 9 классах в рамках обучения по учебникам, выпускаемым издательствами «Просвещение» и «Мнемозина». Авторские программы составлены в соответствии с требованиями, предъявляемыми как к базовому (3 часа в неделю), так и к профильному (4 часа в неделю) уровню обучения, а также углубленному изучению (5 часов в неделю). При этом авторами программ и учебников предлагаются различные структуры учебного материала, которые определяют последовательность изучения материала в рамках стандарта для средней школы и пути формирования системы знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования, а также развития учащихся.
Планирование темы «Прогрессии» разными авторскими коллективами.
1 вариант: 3ч в неделю
2 вариант: 4ч в неделю
3 вариант: 5ч в неделю
| АВТОРЫ ПРОГРАММЫ | КОЛ – ВО ЧАСОВ |
| 1 | 2 | 3 |
|
Ю.Н. Макарычев и др. (после изучения раздела «Уравнения и неравенства с двумя переменными»)
|
15 |
17 |
- |
|
Ш.А. Алимов и др. (после изучения раздела «Элементы тригонометрии»)
|
14 |
18 |
- |
|
Г.В. Дорофеев и др. (после изучения раздела «Уравнения и системы уравнений»)
|
17 |
24 |
- |
|
Н.Я. Виленкин (после изучения раздела «Уравнения и системы уравнений»)
|
- |
18 |
24 |
|
И.И. Зубарева, А.Г. Мордкович (после изучения раздела «Числовые функции»)
|
16 |
- |
28 |
Я преподаю в 9 общеобразовательном классе без углубленного обучения математике и предпрофильной подготовки. В своей работе использую УМК А, Г. Мордковича (Алгебра – 9 учебник, Алгебра – 9 задачник, Алгебра – 9 контрольные работы, Алгебра 7 – 9 тесты, Алгебра 7 – 9 методическое пособие для учителя) издательства «Мнемозина». Особенность УМК состоит в том, что он основан на принципах проблемного, развивающего и опережающего обучения.
-7-
Поурочное планирование по разделу «Прогрессии» взято из «Программы. Математика 5-6 классы. Алгебра 7-9 классы. Алгебра и начала анализа 10-11 классы» авторы- составители И.И.Зубарева, А.Г. Мордкович, издательство «Мнемозина», Москва, 2007 год.
Поурочное планирование по разделу «Прогрессии»
(после изучения главы 3 «Числовые функции»).
В большинстве действующих школьных учебниках тема «Прогрессии» в 9 классе – тупиковая, не имеющая связей с остальным материалом основной школы, а тупиковых тем в разумно выстроенной программе быть не должно. Последовательности – тема математического анализа, и было бы логичнее начинать с нее изучение начал математического анализа в старшей школе. А прогрессии – частные случаи последовательностей, искусственно вырвать их из общей темы в принципе не целесообразно.
Но, в стандарте математического образования тема «Прогрессии» представлена в рамках основной школы, значит, мы обязаны ее рассматривать в курсе алгебры 9 класса, позаботившись о том, чтобы эта тема была органично связана с предыдущими разделами курса и не была тупиковой. Поскольку в УМК А. Г. Мордковича приоритет отдается функциональной линии, то и последовательности подаются в том же ключе. Это функции, но несколько отличающиеся от того, к чему привыкли ученики; это – функции
натурального аргумента.
| НОМЕР ПУНКТА | СОДЕРЖАНИЕ МАТЕРИАЛА | КОЛ – ВО ЧАСОВ |
| Глава 4. 14 15 16 | Прогрессии. Числовые последовательности. Арифметическая прогрессия. Геометрическая прогрессия. Контрольная работа №6. | 16 4 5 6 1 |
В данное поурочное планирование мною внесены некоторые коррективы. Цель: сэкономить часы, чтобы присоединить их в дальнейшем к итоговому повторению курса алгебры 9 класса. Экономия времени получается за счет использования уроков – лекций, на которых дается теоретический материал блоком, а не по частям.
| НОМЕР ПУНКТА | СОДЕРЖАНИЕ МАТЕРИАЛА | КОЛ – ВО ЧАСОВ |
| Глава 4. 14 15 16 | Прогрессии. Числовые последовательности. Арифметическая прогрессия. Геометрическая прогрессия. Контрольная работа №6. | 13 3 4 5 1 |
-8-
5. Психолого-педагогическое объяснение специфики восприятия и освоение учебного материала учащимися в соответствии с возрастными особенностями.
Можно выделить основные потребности возраста: потребность в активном социальном взаимодействии со сверстниками, в интимно-личностном общении, в самовыражении, самоутверждении, творчестве. Причем, реализация этих потребностей сопряжена с высокой степенью эмоциональной незрелости подростков. Следовательно, процесс обучения подростков будет эффективным только в том случае, если деятельность, предложенная им, будет отвечать их потребностям и соответствовать ведущей деятельности. Только при этом обучение для учащихся будет мотивированным, а, следовательно, вероятность их продуктивного включения в данный процесс существенно повысится.
Важно отметить, что по мере взросления возрастает влияние индивидуальных особенностей на процесс развития. В подростковом возрасте наблюдаются более значительные индивидуальные вариации в развитии.
Работоспособность снижена вследствие вегетативной перестройки, повышенная утомляемость и нестабильность. Старшие подростки могут сознательно управлять своими потребностями, формировать долгосрочные планы и перспективы.
При обучении необходимо учитывать повышенную утомляемость и нестабильность настроения подростков. Легкие и сложные задания, должны чередоваться друг с другом.
Значительные изменения претерпевает познавательная сфера. Развитие восприятия подростка сопоставимо с уровнем развития взрослого человека (он способен качественно выполнить все тесты на восприятие). Поэтому все закономерности восприятия графической информации для взрослых могут использоваться при составлении заданий для учеников 8 классов. Внимание становится более устойчивым и произвольным. Продолжает активно развиваться теоретическое, логическое мышление (стадия формальных операций), а также способность к анализу абстрактных идей и предметов. Если для младшего подростка имеют смысл только те понятия, которые можно представить в какой-либо конкретной, образной форме, то для учащихся 8 классов можно предлагать задания, ориентированные на дальнейшее формирование способностей осмысливать абстракции.
Мышление становится психическим процессом, определяющим развитие других психических (особенно познавательных) процессов. По мере взросления увеличивается кругозор,
накапливаются и систематизируются знания из самых разных жизненных сфер.
Содержание учебного материала может быть представлено:
а) знаниями из многих областей;
б) различными научными точками зрения, что будет способствовать развитию критичности мышления.
Развиваются рефлексивные умения. Предметом осмысливания становятся не только объекты внешнего мира, но и собственные психические состояния, в т.ч. и мыслительные процессы. Появляется возможность анализировать ситуации независимо от реальных обстоятельств. Мышление становится «опережающим», что дает возможность планировать свои действия, прогнозировать развитие событий. Это создает предпосылки для развития воли. Формируется способность к формулированию гипотез (обоснованных предположений о возможных причинах и вероятных последствиях событий).
Уместным представляется использование различных технологических методов и приемов.
Развитие познавательных процессов, и особенно, интеллекта, имеет количественные (подросток решает интеллектуальные значительно легче, быстрее и эффективнее, чем младший школьник) и качественные (сдвиги в структуре мыслительных процессов) особенности.
Это влечет за собой и качественную перестройку в организации мнеммонических
-9-
процессов, развитие логической памяти. Если раньше ученики для того, чтобы запомнить что-нибудь, прибегали к многократному повторению, то для старших подростков важнее выявить смысл изучаемого материала, ключевые идеи и их взаимосвязи. Активно идет освоение мнемонических приемов.
Развитие мышления определяет успешность учебной деятельности – применение мнемонических приемов, приемов работы с информацией, риторических и креативных приемов. Уровень сложности задач и проблем должен создавать для подростков «зону ближайшего развития».
Одной из сфер жизнедеятельности, которая способствует удовлетворению основных потребностей подростка, является игровая деятельность. Это отмечают такие авторы как Рувинский Л.И., Соловьева Л.Е., Краковский А.П. и другие специалисты в области возрастной психологии. Умело организованное игровое действие способно удовлетворить потребности подростков, согласно их ведущему виду деятельности. Включение фрагментов содержания, представленного в игровой форме, инициирует игровые виды учебной деятельности и способствует более глубокому усвоению учебного материала.
Продолжается формирование индивидуального стиля деятельности, учет индивидуально-своеобразных способов представления информации в зависимости от доминирования определенной модальности опыта. Выделены три основные сферы «сенсорного опыта» человека: визуальная, аудиальная, кинестетическая. Соответственно, разные люди принимают и перерабатывают информацию о своем окружении, преимущественно опираясь либо на визуальный опыт (зрительно и с помощью мысленных образов), либо аудиальный опыт (посредством слуха), либо кинестетический опыт (через осязание, обоняние и другие чувственные впечатления).
Для визуала типичная познавательная позиция – смотреть, представлять, наблюдать. Таким учащимся нужно предоставлять возможности больше читать, рассматривать схемы, таблицы, иллюстрации, пытаясь запомнить нужную информацию. Следовательно, содержание должно быть представлено с использованием этих различных средств наглядности.
Для аудиала типичная познавательная позиция – слушать, говорить, обсуждать. Для таких учеников важна возможность проговаривания, обсуждения. Следовательно, содержание должно включать элементы озвучивания, мультимедиа фрагменты.
Для кинестетика типичная познавательная позиция – действовать, чувствовать, ощущать. Таким учащимся важно не просто учить материал, а каким-то образом работать с ним (самостоятельно составлять таблицы, схемы, вписывать формулы, отдельные фрагменты текстов, работать с интерактивными картами и т.д.). Весьма полезны задания, предполагающие краткое конспектирование главных мыслей – составление конспекта, плана ответа и т.д.
Принципы построения учебного содержания, на основе учета возрастных особенностей учащихся
- ориентация на самостоятельное осмысление содержания
- лаконичный стиль изложения учебного материала, отсутствие или весьма ограниченное использование достаточно большого количества подчиненных предложений, отглагольных существительных и нанизывание падежей, для установления иерархических зависимостей и причинно-следственных связей;
- диалогичность изложения;
- проблемность, обеспечивающая активность позиции учащегося в процессе обучения и развивающая творческий потенциал учащегося;
- разнообразие учебного содержания за счет представления в нем: аналитико-логической, образной, практической, алгоритмической, линии введения учебного материала для детей с разными познавательными стилями;
- представление в содержании профессионально знаний, необходимых в будущей самостоятельной жизни (связанных с областью профессиональных интересов, решением проблем личного характера, возможностью самоутверждения себя в статусе взрослого);
- раскрытие в содержании определенной системы ценностей, обеспечивающей развитие собственной системы ценностей учащихся;
-10-
- “гипертекстовость”, обеспечивающая дифференциацию и индивидуализацию образования, через разные формы подачи одной информации с целью лучшего ее освоения учащимися.
-11-
6. Обоснование используемых в образовательном процессе по разделу «Прогрессии» программы образовательных технологий, методов, форм организации деятельности учащихся.
В своей работе я использую технологию развивающего обучения, основоположником которой является Леонид Владимирович Занков (1901-1977г).
Дидактические принципы технологии:
1. Ведущая роль теоретических знаний.
Ученики с помощью учителя делают выводы, определяют закономерности, совершая исследовательски-поисковую работу.
2 Обучение на высоком уровне трудности с соблюдением меры сложности.
Суть его не в увеличении учебной нагрузки и ее сложности, а в преодолении трудностей, доступных ребенку. Такая организация в классе, что решая общую учебную задачу, каждый ребенок решает свою учебную трудность, на своем уровне.
3. Осознание процесса учения.
Этот принцип развивает рефлексию, самоанализ: « Что я знал и что я узнал нового?», « Что мне было интересно?», « Каков я есть?».
4. Быстрый темп прохождения материала.
Быстрый темп не означает торопливости и спешки на уроках. Наоборот, нельзя жалеть времени на уроках на разрешение различных противоречий и проблем. Этот принцип противостоит топтанию на месте, использованию однотипных упражнений при прохождении данной темы.
5. Развитие всех учащихся и сильных, и слабых.
Развитие происходит из сотрудничества разных по уровню детей. Все дети могут продвигаться в развитии. Сам процесс развития идет циклично, поэтому слабые и сильные ученики должны учиться вместе.
Типические свойства технологии:
1. Многогранность.
Многообразие деятельности школьника через вовлечение в сферу учения его разносторонней психической деятельности: эмоциональной, волевой, интеллектуальной, эстетической.
2. Процессуальность.
Раскрытие сущности изучаемого материала в совокупности с постоянным возвратом к ранее пройденному, на основе органической существенной связи старого с новым.
3. Коллизия.
Использование в учебном процессе противоречий, возникающих при столкновении старых знаний с новыми, нового способа действия с усвоенными, старого индивидуального опыта с новыми требованиями его приложения, чувства с разумом.
4. Вариативность.
Различные варианты методов и приемов, учитывая профессиональные склонности учителя и индивидуальные возможности детей.
У детей, которые занимаются по системе Занкова, воспитывается творческое отношение к учению. Школьник учится анализировать, сопоставлять, рассуждать. Система нацеливает ученика на активную работу в классе и дома; способствует развитию способности принимать самостоятельные решения.
При планировании урока в развивающем обучении учитель ищет новые формы работы, направленные на активизацию учебной деятельности. В противовес традиционной системе, где преобладают репродуктивные методы обучения и исполнительская форма взаимодействия, развивающее обучение предполагает развитие мышления ребенка и групповые формы взаимодействия (уроки – дискуссии, проблемные уроки ).
Выход в «зону ближайшего развития» осуществляется:
-12-
-
через уважение ученика и учёт его реальных возможностей и способностей в обучении;
-
через постановку трудных заданий; педагог руководит логикой ответов на поставленный вопрос, предлагает помощь, а не подсказку, тем более готовое решение;
-
предусматривается введение вход урока творческих заданий, использование развивающих упражнений, широкое применение методов сравнения, коллизий, интеграции;
-
использование на уроке минимизма наглядности; наглядность применяется как источник знаний; при опросе наглядность либо совсем не используется, либо даётся как вариант для опоры или вариант нового материала;
-
использование учеником дополнительных сведений из вспомогательных источников
( словарей, энциклопедий, справочников).
Дидактический стержень урока в системе Занкова – это преобразующая деятельность учеников: дети наблюдают, сравнивают, анализируют, классифицируют; обучение идёт косвенным путём,
т. е. главное – развитие детей.
§ 14. Числовые последовательности. Определение числовой последовтельности и способы ее задания. (3ч.)
Урок 1.
Цели: ввести понятие числовой последовательности и членов последовательности; рассмотреть аналитическое задание числовой последовательности.
Выход в «зону ближайшего развития» осуществляется через сравнение и анализ. Предлагаю рассмотреть четыре функции:
-
y = x2`, x  [0;1] 2) y = x2`, x
[0;1] 2) y = x2`, x  [0;∞) 3) y = x2 4) y = x2`, x
[0;∞) 3) y = x2 4) y = x2`, x  N.
N.
В ходе беседы выясняем сходства и различия функций, анализируем их графики. Возникает проблема: встречаются ли в реальной жизни ситуации, математической моделью которых служит функция 4) и надо ли ее изучать? Приводим примеры: 1) На складе имеется 500 т угля, каждый день подвозят по 30 т. Сколько угля буде на складе через день, два, три, пятнадцать дней и т. д.? ; 2) На банковский счет положили а руб., а банк ежемесячно начисляет р%. Сколько денег на счету станет через месяц, два, двенадцать месяцев и т. д.? Примеры убеждают учащихся в том, что функцию 4) нужно изучать, таким образом, мы активизировали их познавательную деятельность.
После введения понятия числовой последовательности, членов последовательности, рассмотрения аналитического задания числовой последовательности, отрабатываем данную математическую модель. Для прочного усвоения модели предлагаю
1. Из предложенных функций выписать числовые последовательности и обосновать свой выбор:
a) y = 2x – 1, x  [0;∞); б) y = 2x – 1, x
[0;∞); б) y = 2x – 1, x  Q; в) y = 2x – 1, x
Q; в) y = 2x – 1, x  Z; г) y = 2x – 1, x
Z; г) y = 2x – 1, x  N,
N,
д) y = 2x+1 / x, x  [0;∞); е) y = 2x+1 / (x2+), x
[0;∞); е) y = 2x+1 / (x2+), x  Q; ж) y = 2x+1 / ( x2+1), x
Q; ж) y = 2x+1 / ( x2+1), x  Z;
Z;
з) y = 2x+1/x, x  N.
N.
2. Назовите члены последовательности (yn), которые: а) следуют за членом y31, yn, yn+9, y2n;
б) предшествуют члену y91; y639; yn-1; y3n; в) расположены между членами y638 и y645; y1002 и y1005;
yn+3 и yn+105; yn-2 и yn+2.
Сосулька тает со скоростью 5 капель в минуту. Сколько капель упадет на землю через 1 мин., 2 мин., 3 мин., 17 мин. и т. д. от начала таяния сосульки?
-
задания на вычисление членов последовательности по заданной формуле и, наоборот, на составление формул по заданным членам, например,
1. Вычислите первые пять членов последовательности по заданной формуле а) ап = 4п+1;
б) ап = -3п – 7; в) ап = 1 /( п + 5); г) ап = - 3 / (4п – 1).
2. Составьте одну из возможных формул п-го члена последовательности по первым пяти ее членам: а) 1, 2, 3, 4, 5, … : б) – 2, - 1, 0, 1, 2, …; в) 1, 3, 5, 7, 9, …; г) 1, 4, 9, 16, 25, …;
д) 3, 6, 9, 12, 15, …; е) 4, 9, 16, 25, 36, …
-13-
Постройте график последовательности: а) yn = (3 – n) / 2; б) yn = n2 – 4; в) yn = 1 / (n+1); г) yn = 3n/ 2.
Задания предлагаются от простого к сложному, что предусматривает развитие вех учащихся и сильных, и слабых. Прослеживается процессуальность и коллизия.
На дом предлагается составить кроссворд по новой теме (см. приложение 7).
Урок 2.
Цели: рассмотреть словесный и рекуррентный способы задания последовательности и закрепить их знание в ходе выполнения упражнений; вырабатывать навыки и умения при нахождении членов последовательности по формуле.
Математический диктант – одна из форм контроля знаний. Цели данного вида работы: проверка уровня готовности учащихся к дальнейшей работе; научить учащихся слышать, слушать и понимать язык математики. При такой форме работы можно использовать метод «закрытой доски»: ответы диктанта записаны на обратной стороне доски, по окончании работы доска открывается, ученики осуществляют самопроверку или взаимопроверку.
На данном уроке выход в «зону ближайшего развития» осуществляется с помощью математического диктанта с последующей взаимопроверкой и обсуждением результатов:
-
Сформулируйте определение числовой последовательности.
-
Назовите способы задания числовой последовательности.
-
Последовательность (yn) задана формулой yn = 6n – 1. Найдите y1; y4; y20; y100; yk.
( 5; 23; 119; 599; 6к – 1)
-
Составьте одну из возможных формул n-го члена последовательности по первым пяти ее членам: 6; 7; 8; 9; 10; … (yn = n + 5)
-
Запишите последовательность простых чисел. (2; 3; 5; 11; 13; 17; 19; 23; 29; …)
Обсуждение последнего задания диктанта приводит к постановке учебной задачи: научиться задавать последовательность словесно и рекуррентно.
После изложения теоретического материала в соответствии с текстом учебника, закрепляем и отрабатываем его, используя № 383; 384; 393; 394 из задачника. Учитель пишет на доске, дети по цепочке комментируют с места, записывая в тетрадь. Такой способ отработки позволяет вовлечь в работу большую часть класса, овладеть устным и письменным математическим языком, развивает внимание.
На дом предлагаю творческую работу: каждый ученик должен составить карточку, в которой
он задает три последовательности, каждую из которых только одним способом. На уроке учащиеся меняются своими карточками и заполняют пустые места. Проверяет работу тот, кто составил карточку. Каждый ученик получает двойную пользу: во-первых, составляя карточку, он должен уметь заполнить ее сам, чтобы правильно оценить работу товарища; во-вторых, на уроке каждый заполняет карточку, составленную своим товарищем, а для этого нужно знать способы задания числовой последовательности.
Примерный вид карточки:
| СПОСОБЫ ЗАДАНИЯ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ |
ФОРМУЛОЙ N-ГО ЧЛЕНА |
СЛОВЕСНО |
РЕКУРРЕНТНО |
ПЕРВЫЕ ПЯТЬ ЧЛЕНОВ ПОСЛЕДОВА ТЕЛЬНОСТИ |
|
1.
|
n2 |
|
|
|
|
2. |
| Последователь-ность всех натуральных чисел, кратных семи. |
|
|
|
3. |
|
|
x1 = 1 xn = 2 + xn- 1
|
|
Урок 3.
Цели: закрепить знание учащимися способов задания числовой последовательности; изучить свойства числовых последовательностей и научить применять их в ходе выполнения упражнений; развивать логическое мышление.
После работы с карточками, изготовленными дома, их проверки и выставления оценок, учащимся предлагается самостоятельная работа с учебником по группам:
Iгруппа – составить рассказ о возрастающей последовательности;
II группа - составить рассказ об убывающей последовательности по плану:
-
Определение числовой последовательности.
-
Свойства присущие ей как функции.
-
На каком свойстве остановимся более подробно.
-
Определение возрастающей (убывающей) последовательности.
-
Привести не мене трех примеров с обоснованием.
III группа – составить алгоритм, пользуясь которым можно доказать, что последовательность является монотонной. Показать работу алгоритма на примере № 385 (а, в)
Задания у групп разные по уровню: I и II - воспроизведение материала; III – творческое. После самостоятельной групповой работы заслушиваем отчет представителей групп.
Далеt учащиеся самостоятельно отрабатывают алгоритм, учитель по необходимости помогает.
Коллективная групповая форма деятельности во многих случаях создает личную мотивацию. Групповая форма «втягивает» в активную работу даже пассивных, слабо мотивированных учащихся, так как они не могут отказаться выполнять свою часть работы, не подвергнувшись осуждениям со стороны товарищей. Кроме того, подсознательно возникает установка на соревнование, желание быть не хуже других.
§ 15. Арифметическая прогрессия (4ч.)
Урок 1.
Цели: дать определение арифметической прогрессии, вывести формулу n-го члена арифметической прогрессии.
Изложение нового материала ведется в форме лекции, после чего предлагается самостоятельная работа воспроизводящего характера. Работе воспроизводящего характера (по образцу, по инструкции или алгоритму, с промежуточными записями, с указаниями к решению и др.) способствует психологический настрой на успех. На этом уровне происходит подготовка к самостоятельной деятельности. Работа по инструкции или алгоритму применяется для закрепления изученного материала, соответствует низкому уровню самостоятельности, может применяться для учащихся с любым уровнем обучаемости.
Вид карточки:
Найдите разность и десятый член арифметической прогрессии 100; 90; 80; 70; …
Алгоритм решения:
-
Запишите чему равны а1 и а2.
-
Вычислите разность по формуле d= а2 - а1.
-
Вычислите десятый член по формуле аn = а1 + d(n – 1)
-
Запишите ответ.
Готовим воспроизводящие карточки для разнотипных заданий:
-
Составление формул n-го члена арифметической прогрессии;
-
Нахождение любого члена прогрессии по известному первому и разности;
-
Нахождение разности прогрессии, если известны любые два ее члена;
-
Нахождение первого члена прогрессии, если известны разность и любой ее член;
-
Нахождение разности прогрессии и ее первого члена, если известна формула n-го члена (смотри приложение 1).
Урок 2.
Цели: учить учащихся решать задачи, используя формулу n-го члена арифметической прогрессии.
В начале урока использую карточки для устного счета
-15-
| Выбери последовательность, которая является арифметической прогрессией |
|
| А | Б | В | Г |
| 1. | 34; 33; 31; 28; … | 45; 15; 5; 1; … | 12; 17; 22; 27; … | 29; -28; 27; -26; … |
| 2. | 7; 14; -7; -14; 14; 21; … | -8; -5; -2; … | -40; -39; -38; 38; 39; 40; -37; -36; .. | -7; 2; -6; 3; -5; 4; … |
| 3. | 81; 9; 1; 1/9; … | 2; 4; 3; 6; 4; 8; … | -3,7; -1,7; 0,3; 2,3; … | 1; 2; 3; 4; …
|
| 4. | 0; 0,5; 1; 1,5; … | 32; 16; 8; 44 … | 94; 80; 66; 52; … | 1,2; 2,7; 4,2; 5,7; … |
| Найди разность арифметической прогрессии. |
| 15; 30; 45; … | 15 | -15 | 2 | 0,5 |
| 30; 40; 50; … | 10 | -10 | 3/4 | 4/3 |
| -10; -5; 0; 5; … | -15 | -5 | 5 | 2 |
| 4; 8; 12; 16; … | 2 | 1/2 | -4 | 4 |
| 35; 30; 25; 20; .. | 5 | -5 | 7/6 | 6/7 |
В течении урока можно использовать игровые моменты:
-
Учитель: Я задумал некоторую арифметическую прогрессию. Задайте мне только два вопроса, чтобы после ответов вы быстро смогли бы назвать первый член этой прогрессии.
-
Учитель записывает на доске любое число, например 60. Учащиеся должны придумать арифметическую прогрессию, чтобы сумма трех ее членов была равна 60. Кто больше придумает таких прогрессий?
-
На доске записано 20 чисел: 1; 4; 7; 10; 13; 16; 19; 22; 25; 28; 31; 34; 37; 40; 43; 46; 49; 52; 55; 58. Учитель стоит спиной к доске. Ученики называют номер числа, а учитель мгновенно называет само число. Потом он предлагает учащимся объяснить, как ему это удается.
Создание игровых моментов на уроках математики повышает интерес к предмету, вносит разнообразие и эмоциональную окраску в учебную работу, снимает утомление, развивает внимание, сообразительность, чувство состязательности и взаимопомощи, прививает навыки коллективной работы.
Урок 3.
Цели: вывести формулу суммы n первых членов арифметической прогрессии и научить применять ее при решении упражнений.
Начинаю урок с контролирующей самостоятельной работы:
|
Вариант 1. -
В арифметической прогрессии известны а1 = - 1,2 и d = 3. Найдите а4; а8; а21. -
Найдите разность арифметической прогрессии (аn), если а1 = 2; а11 = - 5. -
В арифметической прогрессии известны а1 = - 12 и d = 3. Найдите номер члена прогрессии, равного 9. -
Выписали двадцать членов арифметической прогрессии 6,5; 8; … Встретиться ли среди них число 36?
|
Вариант 2. -
В арифметической прогрессии известны а1 = - 0,8 и d = 4. Найдите а3; а7; а24. -
Найдите разность арифметической прогрессии (аn), если а1 = 4; а18 = - 11. -
В арифметической прогрессии известны а1 =14 и d = 0,5. Найдите номер члена прогрессии, равного 34. -
Выписали двадцать членов арифметической прогрессии 18; 4 … Встретиться ли среди них число -38?
|
Перед объяснением нового материала в форме лекции, активизирую познавательную деятельность учащихся, рассказывая предание о маленьком Карле Гауссе, будущем немецком короле математики XIX века, решившем в возрасте пяти лет очень быстро задачу о нахождении суммы первых ста натуральных чисел. Предложить учащимся решить эту задачу.
-16
Урок 4.
Цели: изучить характеристическое свойство арифметической прогрессии; способствовать выработке навыков и умений решения задач с использованием формул суммы n первых членов арифметической прогрессии; закрепить изученный материал.
В начале урока провожу контролирующий «экспресс – диктант». Он проводится как и обычный диктант, но ответы записываются в двух экземплярах (под копирку). Контрольный экземпляр сдается учителю, по оставшемуся экземпляру идет фронтальная проверка. Бывает, что слуховому восприятию нужно помочь. В этом случае одновременно с чтением делаю запись чисел на доске.
Пример такого диктанта (в квадратных скобках указаны данные для 2 варианта):
-
У арифметической прогрессии первый член 4 [ 6 ], а второй член 6 [ 2 ]. Найдите разность.
-
У арифметической прогрессии первый член 6 [ 4 ], а второй член 2 [ 6 ]. Найдите третий член.
-
Найдите 10-й [ 8-й ] член арифметической прогрессии, если ее первый член равен 1, а разность равна 4 [ 5 ].
-
Является ли последовательность четных [ нечетных] чисел арифметической прогрессией?
-
Является ли последовательность простых [ составных] чисел арифметической прогрессией?
-
Найдите суму первых пяти членов арифметической прогрессии, если ее первый член равен 6 [ - 20 ], а пятый член – 6 [ 20 ].
-
Найдите суму первых пяти членов арифметической прогрессии, если ее первый член равен – 20 [ 6 ], а разность равна 10 [ - 3 ].
Школьников необходимо учить самостоятельно добывать знания и совершенствовать их. В процессе самостоятельной деятельности развиваются такие ценные качества личности как внимательность, настойчивость, точность, ответственность. Работа с учебником – это один из видов самостоятельной работы. Характеристическое свойство арифметической прогрессии изучается с применением работы по учебнику под руководством учителя.
На дом дается творческая работа: составить карточку с пустыми ячейками и на следующем уроке предложить ее соседу по парте в качестве домашнего задания. Таким образом, каждому придется систематизировать свои знания по теме «Арифметическая прогрессия», что будет необходимым на следующем уроке. Карточка может выглядеть так:
| а1 | d | аn | n | Sn |
| 7 | 4 |
| 13 |
|
| 2 | 2 | 80 |
|
|
| 56 |
| 26 | 11 |
|
| 2 |
| 87 |
| 801 |
|
|
| 21 | 7 | 105 |
На 3 и 4 уроках можно предложить учащимся тесты (см. приложения 8-10)
§ 15. Геометрическая прогрессия (5ч.)
Урок 1.
Разработка этого урока приведена подробно в пункте 8. Урок проводится с использованием компьютерных технологий.
Урок 2.
Цели: вывести формулу суммы n первых членов геометрической прогрессии, вырабатывать навыки применения формул n-го члена, суммы n первых членов, характеристического свойства.
В виде игровой ситуации учащимся предлагается задача, которая содержит жизненные факты, но при решении которой возникает необходимость в выводе новой формулы.
Задача. Однажды незнакомец постучал в окно к богатому купцу и предложил такую сделку: «Я буду ежедневно в течение 30 дней приносить тебе по 100000 р. А ты мне в первый день за 100000 р. дашь 1 коп., во второй день за 100000 р. – 2 коп. и так каждый день будешь увеличивать предыдущее число денег в два раза. Если тебе выгодна сделка, то с завтрашнего дня начнем». Купец обрадовался такой удаче. Он подсчитал, что за 30 дней он получит от незнакомца
3000000 р. На следующий день они пошли к нотариусу и оформили сделку.
-17-
Создается проблемная ситуация. Кто в этой сделке проиграл: купец или незнакомец? Учащиеся
составляют последовательность чисел: 1; 2; 4; 8; 16; 32; 64; 128; 256; … Убеждаются, что эта последовательность является геометрической прогрессией со знаменателем q = 2, первым членом а1 = 1 и количеством членов n = 30. Большинство ребят стремятся составить всю последовательность, чтобы потом найти ее сумму. Но видят, что это громоздкая работа, которая требует времени. Обращаются с вопросом к учителю: «Можно ли подсчитать по формуле сумму нескольких первых членов геометрической прогрессии?» Учитель дает утвердительный ответ при этом усиливает проблемность, рассказывая историю о награде изобретателя шахматной игры: «По преданию, индийский принц Сирам, восхищенный остроумием игры и разнообразием возможных положений шахматных фигур, призвал к себе ее изобретателя, ученого Сету, и сказал ему: «Я желаю достойно вознаградить тебя за прекрасную игру, которую ты придумал. Я достаточно богат, чтобы исполнить любое твое желание». Сета попросил принца положить на первую клетку шахматной доски 1 пшеничное зерно, на вторую – 2 зерна, на третью – 4 зерна и т. д.». Возникает необходимость найти S64, где а1 = 1, q = 2, n = 64. Под руководством учителя учащиеся выводят формулу Sn. Убеждаются, что купец проиграл.
Далее отрабатываем формулы, полученные на этом и предыдущем уроках.
Для отработки можно использовать тренажер. Основное назначение карточек-тренажеров – формировать у учеников прочные вычислительные навыки, одновременно развивая внимание и оперативную память. Карточку целесообразно использовать как на этапе введения новых действий, так и на этапе их отработки. Карточки-тренажеры рассчитаны на многократное использование. Задания тренажера предлагаются учащимся для коллективной работы в классе, для работы в парах, а также для индивидуальной и домашней работы. (смотри приложение 12)
Урок 3,4.
Цели: закрепить знание формул геометрической прогрессии, способствовать выработке навыков и умений решения систем уравнений.
Начать первый из этих уроков можно с самостоятельной работы, которая поможет проконтролировать знание формул и применения их в стандартных ситуациях. Можно сразу осуществить взаимопроверку.
| 1 вариант | 2 вариант |
|
-
Найди первые шесть членов геометрической прогрессии, если b1 = - 1 q = 3. -
Найдите знаменатель геометрической прогрессии 3; 9; 27; … -
Найдите сумму первых пяти членов геометрической прогрессии, у которой b1 = 14, q = ½. |
-
Найди первые шесть членов геометрической прогрессии, если b1 = - 1 q = - 3. -
Найдите знаменатель геометрической прогрессии 2; 1: 0,5; … -
Найдите сумму первых пяти членов геометрической прогрессии, у которой b1 = 6, q = 1/3. |
:
Ответы (можно вынести на закрытую доску):
| № задания | 1 | 2 | 3 |
| 1 вариант | - 1; -3; -9; -27; -81. | 3 | 217/8 |
| 2 вариант | - 1; 3; -9; 27; -81 | 1/2 | 242/27 |
Для активизации познавательной деятельности можно использовать прикладные задачи:
-
Сосчитайте сколько мух появилось бы за полгода от одной пары, если бы их потомство не погибало, а полностью сохранялось. Муха откладывает 160 яиц, будем считать, что в новом поколении половина самок, они становятся взрослыми через 20 дней и откладывают яйца только один раз. Чтобы представить себе количество мух через 6 месяцев, оцените, как они будут распределены по всей суше.
Справка. Площадь суши на земле 1,5 * 108 км ≈ 1,5 * 1014
-18-
Ответ: 2(1 + 80 + 802 + … + 808) = 2(809 – 1)(80 – 1) = 3,4 * 1015; 23 мухи на каждый квадратный метр суши.
-
Для трансформатора допускается перегрузка в течение 20 мин на 75% от нормального тока. С увеличением времени перегрузки на каждые 20 мин допустимый уровень снижается до 0,8 от предыдущего. Каковы допустимые перегрузки трансформатора, работающего
1, 2, 3 ч?
Ответ: 48 %, 24,6 %, 12,6 %.
Закончить последний урок тестом:
| № | 1 вариант | 2 вариант | А | Б | В | Г |
| 1. | Найдите первый член геометрической прогрессии b1; b2; 4; - 8 … | Найдите четвертый член геометрической прогрессии 8; - 4 …
|
1 |
- 1 |
- 28 | ½ |
| 2. | Дана геометрическая прогрессия 1; 3/2; …Найдите номер члена этой прогрессии, равного 729/64 | Дана геометрическая прогрессия 8; - 4 . .. Найдите номер члена этой прогрессии, равного 1/32 |
8 |
9 |
7 |
Нет такого номера
|
| 3. | Найдите сумму первых шести членов геометрической прогрессии, заданной формулой bn = 3n-2 | Найдите сумму первых десяти членов геометрической прогрессии, заданной формулой bn = 2n-3 |
728/3 |
511 |
1023/4
|
364/3 |
| 4 | Третий член геометрической прогрессии равен 2, а шестой равен 54. Найдите первый член прогрессии. | Сумма второго и третьего членов геометрической прогрессии равна 6, а знаменатель 2. Найдите первый член прогрессии.
|
1 |
- 1 |
2 |
2/9 |
| 5. | Сколько членов геометрической прогрессии -48; 24; … больше числа 0,1?
| Сколько членов геометрической прогрессии 18; - 6 … больше числа 0,01?
|
4 |
5 |
6 |
8 |
Коды правильных ответов:
| 1 вариант | А | В | Г | Г | А |
| 2 вариант | Б | Б | В | А | А |
или разноуровневыми карточками (см. приложение 12)
Урок 5.
Цель : повторить весь материал главы, подготовиться к написанию контрольной работы.
Материал подбирается аналогичный контрольной работе. За основу можно взять домашнюю контрольную работу № 4 из учебника. Например, 1 вариант выполнить в классе, а 2 вариант предложить в качестве домашнего задания.
Можно использовать на уроке и тестовые задания. Пример такого задания приведен в приложении 11.
Контрольная работа по теме «Прогрессии» (в скобках указано задание для второго варианта)
-19-
(26; 23; 20; …). Вычислите сумму первых десяти (двенадцати) ее членов.
2.Найдите восьмой (девятый) член геометрической прогрессии 16/27; 16/9; 16/3; …
(15/256; 15/64; 15/16; …)
3.Сумма третьего и шестого (восьмого и второго) членов арифметической прогрессии равна 3 (4). Второй (третий) ее член на 15 больше седьмого (на 12 меньше шестого). Найдите первый и второй (второй и третий) члены этой прогрессии.
( x – 1 ; x + 1 ; 2x + 5) являются тремя последовательными членами геометрической прогрессии.
Каждый вариант контрольной работы состоит из трех частей.
Первая часть работы (задания 1 – 3) включает материал, соответствующий базовому уровню подготовки учащихся. Здесь проверяется тот минимум знаний материала по теме, без которого девятиклассник не может успешно усваивать последующие разделы курса алгебры и смежных дисциплин. В большинстве случаев это одно – двух шаговые задания, они являются составной частью более сложных заданий.
Вторая часть (задание 4) содержит задание, которое выполняется в несколько шагов.
Задания последней части (задание 5) позволяет ученикам показать более высокий уровень знаний, способность применять их в нестандартных ситуациях, проявить повышенный интерес к предмету.
Критерии оценок:
«5» - правильное выполнение всех заданий.
«4» - правильное выполнение первой и второй частей.
«3» - выполнение только первой части.
Оценки «3» , «4» . «5» выставляются при успешном выполнении всех заданий первой части контрольной работы (допускается наличие только одной несущественной ошибки или погрешности.
Для обеспечения благоприятных условий при проведении контрольной работы, следует раздать их тексты каждому ученику, присутствующему в классе.
-20-
7. Система знаний и система деятельности.
Система знаний включает в себя:
-
Знания из определенной научной области (гуманитарные науки: экономика, биология, история; естественные науки: физика);
-
Фундаментальные знания (определение числовой последовательности, ее разновидностей: арифметической и геометрической прогрессии, способов их задания, вычисления их основных характеристик, основные способы решения систем уравнений, решение неравенств)
-
Знания профильного характера, учитывающие способности и умения учащихся, их подготовку к будущей профессии .
Система деятельности включает:
-
Познавательная и преобразующая деятельность: анализ, сравнение, классификация, наблюдение и постановка проблемы (встречаются ли в реальной жизни ситуации, математической моделью которых служит функция y = x2`, x  N и надо ли ее изучать?), умение ставить цель, выдвигать гипотезу, искать пути решения проблемы, решать ее и делать выводы, моделирование реальных жизненных ситуаций (например. § 14 урок 1, § 15 урок 1, 2).
N и надо ли ее изучать?), умение ставить цель, выдвигать гипотезу, искать пути решения проблемы, решать ее и делать выводы, моделирование реальных жизненных ситуаций (например. § 14 урок 1, § 15 урок 1, 2).
-
Общеучебная деятельность: организация учебного места, способы поиска информации (интернет, дополнительная литература), самостоятельная работа с учебником( написание алгоритмов, творческих работ, составление математических моделей), навыки общения (монолог, диалог, дискуссия, способы слушать и задавать вопросы), методы взаимообучения, организация работы в группе, взаимооценка (нпример, § 14 урок 2)
-
Самоорганизующая деятельность: самостоятельная постановка целей и техника планирования (при написании самостоятельных и контрольных работ, выполнения творческих заданий), самоконтроль, самоанализ, осознание своего продвижения («решил сам», «догадался», «помог товарищу», «принес пользу»).
-21-
8. Разработка урока.
На геометрическую прогрессию отводится 5 часов. Данный урок является первым. На нем вводится понятие геометрической прогрессии через ее характеристическое свойство, вводится формула n- го члена. Модели, полученные на уроке, закрепляются и отрабатываются на следующих уроках.
На основе модели геометрической прогрессии в дальнейшем будет введена модель бесконечно убывающей геометрической прогрессии.
Визитная карточка урока.
Предмет: математика
Тема урока: геометрическая прогрессия
Тип урока: постановка учебной задачи
Учебная задача: введение понятия геометрической прогрессии и ее характеристических свойств
Цели урока:
Образовательная – учащиеся узнают о новой математической модели – геометрической прогрессии и о ее характеристических свойствах.
Развивающая – учащиеся сталкиваются с проблемой, обозначают ее, выдвигают гипотезы, ищут решение проблемы.
Воспитательная – учащиеся осознают необходимость создания новой математической модели применительно к конкретной ситуации.
Структура урока.
-
Мотивационно – ориентировочный этап.
2. Операционально – исполнительский этап.
3. Рефлексивно – оценочный этап.
Средства обучения:
-
компьютер
-
проектор
-
принтер
-22-
Сценарий урока.
I. Мотивационно-ориентировочный этап.
1. Вхождение в контакт.
-Здравствуйте, садитесь. Как настроение? Сегодня нам предстоит много работы. Давайте договоримся быть внимательными, следить за логикой рассуждений. В качестве экономии времени работаем сидя, не забываем правило поднятой руки. Желаю успехов!
В тетради дата, классная работа. Оставьте место для темы урока, ее мы сформулируем позже.
2. Актуализация предыдущего опыта, создание ситуации успеха.
(На экран выводится задача с вопросами к ней (см. приложение 1). Учитель читает. Некоторое время в классе тишина, ученики обдумывают. После чего идет обсуждение вопросов с записью на доске и в тетрадях.)
Задача 1.
Вертикальные стержни фермы имеют такую длину: наименьший – 5дм, а каждый следующий – на 1,5дм длиннее. Записать длину 7 стержней.
| Учитель | Ученики |
| Записать последовательность в соответствии с условием задачи. | 5; 6,5; 8; 9,5; 11; 12,5; 14 |
| Записать эту последовательность с помощью таблицы. | n | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| аn | 5 | 6,5 | 8 | 9,5 | 11 | 12,5 | 14 |
| Найти разность между предыдущим и последующим членами последовательности. | а2 – а1 = 1,5 а.3 – а2 = 1,5 |
| Запишите в общем виде. | аn+1 – аn = d |
| Как называется эта последовательность? | Арифметическая прогрессия. |
| Задать последовательность рекуррентным способом. | a2 = a1 + 1,5 a3 = a2 + 1,5 = a1 +1,5*2 a4 = a3 + 1,5 = a1 + 1,5*3 аn = an-1 + 1,5 |
| Учитель | Ученики |
| Запишите формулу n-го члена. | аn = a1 + 1,5*(n – 1) |
| Это для данной арифметической прогрессии, а если для любой? | an = a1 + d*(n – 1) |
| Что такое d? | Число d = an+1 – an называют разностью арифметической прогрессии. |
| Как называют данную последовательность? Дать ее определение. | Числовая последовательность a1 a2 a3…an называется арифметической прогрессией, если для всех натуральных n выполняется равенство an+1 = an +d, где d разность арифметической прогрессии, о которой было сказано раньше. |
| Каким характеристическим свойством обладает эта прогрессия? Проверьте его для данной последовательности. | Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. 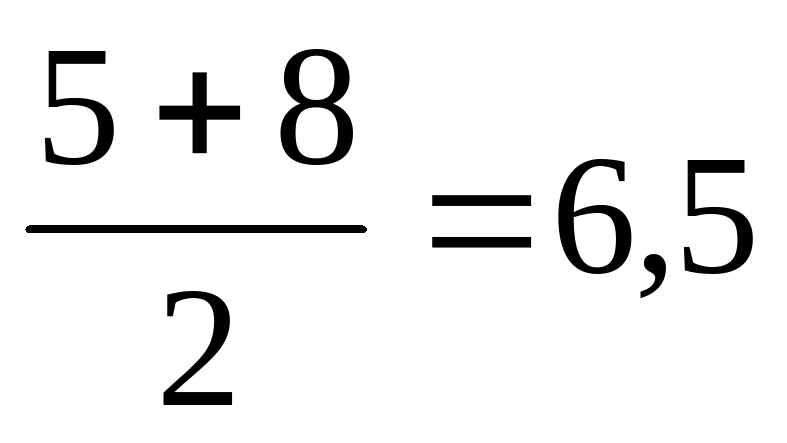 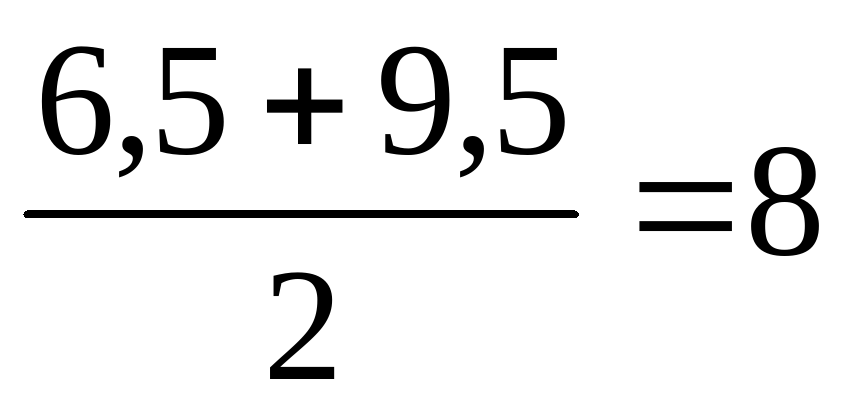
|
| 7. Докажите, что 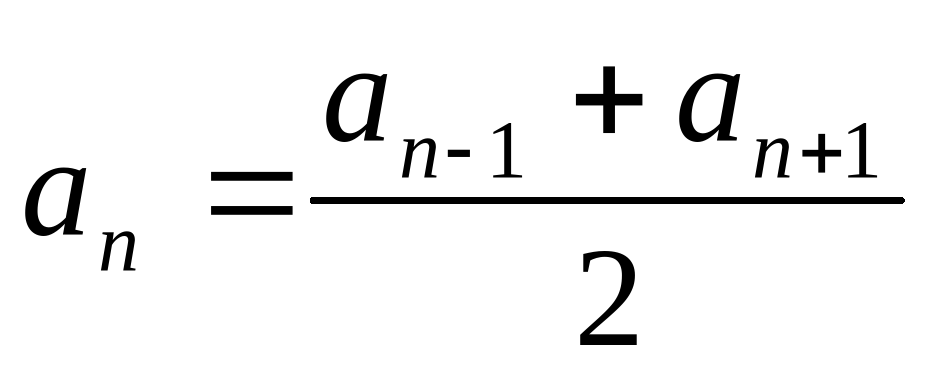
| an-1 = an – d a n+1 = an + d n+1 = an + d an-1 + an+1 = 2an 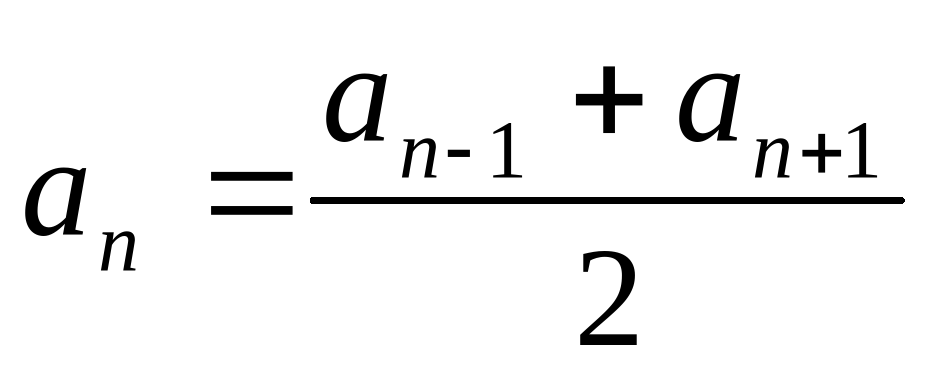
|
| 8.Записать формулу суммы n-членов арифметической прогрессии. Вычислить сумму всех членов данной прогрессии. | 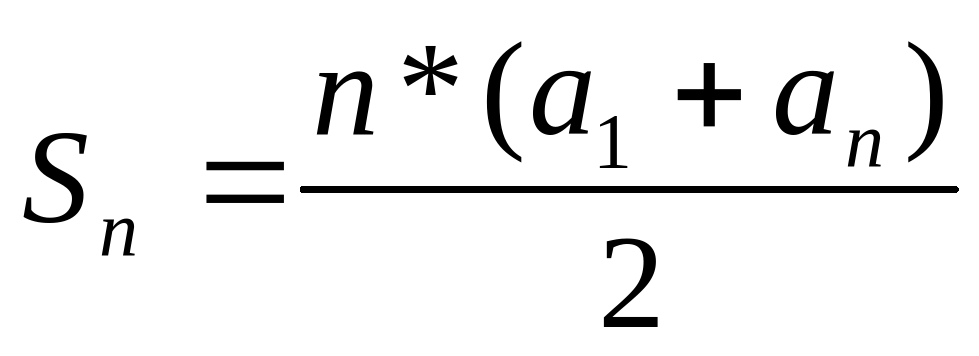
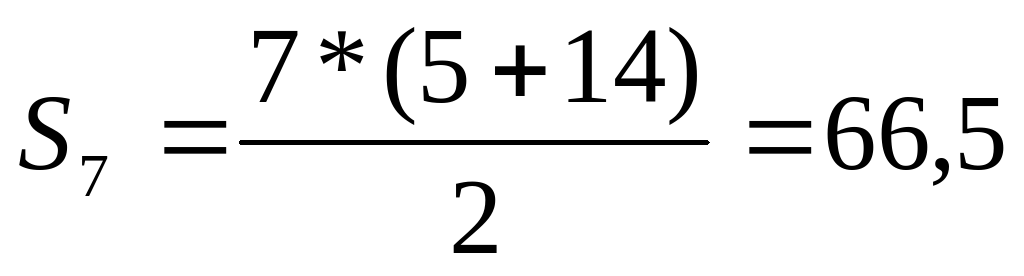
|
| Учитель | Ученики |
| Итак, систематизируем то, что повторили в таблицу. Они лежат у вас на столе. (см. приложение 2) |
|
(Дается время на заполнение таблицы, после чего идет проверка. Заполненная таблица выведена на экран (см. приложение 3)).
3. Постановка учебной задачи.
| Учитель | Ученики |
| А теперь посмотрите еще одну задачу. |
|
(На экран выводится слайд с 2 задачами (см. приложение 4.))
Задача 2.
В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Записать колонию, рожденную одной бактерией за 7 минут.
| Учитель | Ученики |
| Запишите последовательность в соответствии с условием задачи. | 1; 2 ; 4 ; 8 ; 16 ; 32 ; 64 |
| З апишите эту последовательность с помощью таблицы. апишите эту последовательность с помощью таблицы. | n 1 2 3 4 5 6 7 an 1 2 4 8 16 32 64 |
| Найдите разность между предыдущим и последующим членами последовательности. | a2 – a1 = 2 – 1 = 1 a3 – a2 = 4 – 2 = 2 a4 – a3 = 8 – 4 = 4 |
| Подходит данная последовательность под известную модель? | Нет. |
| Это арифметическая прогрессия? | Нет. |
| Почему? | В этой последовательности каждый последующий член не равен предыдущему, сложенному с одним и тем же числом, т.е. не выполняется
|
| Учитель | Ученики |
|
| равенство an+1 = an + d |
| Итак, у нас возникла проблема. Данный вид последовательности не подходит под уже известную модель арифметической прогрессии. |
|
| Сформулируйте задачу нашего урока. | Выяснить вид прогрессии, дать ее название, выяснить ее свойства. |
II. Операционально-исполнительский этап.
| Учитель | Ученики |
| Посмотрите внимательно на эту последовательность. Найдите закономерность в ее построении. Как получается каждое последующее число из предыдущего? | an = an*q |
| Дайте определение этой последовательности. | Это последовательность, каждый член которой равен предыдущему, умноженному на одно и то же число. |
| Может быть вы видите еще какую-нибудь закономерность? | 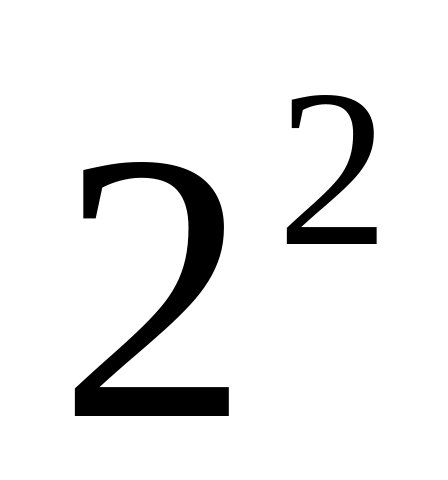 = 4*1 = 4*1
 = 2*8 = 2*8
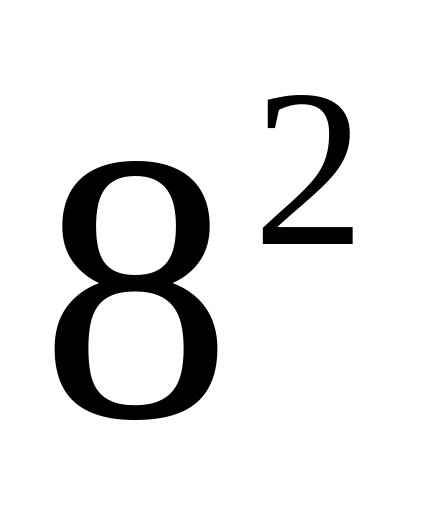 = 4*16 = 4*16
|
| Как называют эту закономерность? | Среднее геометрическое. |
| Как же тогда назовем нашу последовательность? | Геометрическая прогрессия. |
| Итак, тема нашего урока «Геометрическая прогрессия», запишите ее.
|
|
| Учитель | Ученики |
| Какая же последовательность называется геометрической прогрессией? | Числовая последовательность, каждый член которой получается из предыдущего члена умножением на одно и то же число, называют геометрической прогрессией. |
(После формулировки учениками определения, оно выводится на экран (см. приложение 5))
| Учитель | Ученики |
| Сравните его со своим. |
|
| Какое здесь есть уточнение? |
|
| Почему не может быть 0? |
|
| Геометрическую прогрессию обозначают так b1 b2 b3…bn… |
|
| И для нее выполняется равенство bn+1 = bn*q |
|
| Задайте прогрессию рекуррентным способом. | b1 b2 = b1*q b3 = b2*q =b2*q*q =b2*q b4 = b1*q …………. |
| Проанализируйте запись и создайте модель n-го члена геометрической прогрессии. | bn = b1*q |
| Запишите в виде модели характеристическое свойство этой прогрессии. Попробуйте его доказать. | bn = bn+1* bn-1 = bn+1* bn-1 |
|
| bn+1= bn* q b n-1= n-1= bn+1* bn-1 = bn |
(Учитель чувствует, что урок подходит к концу, поэтому переходит к завершающему этапу.)
III. Рефлексивно-оценочный этап.
| Учитель | Ученики |
| Какое значение имеет для вас сегодняшний урок? Что вы узнали? Что поняли? Какие задачи на следующий урок? | Сегодня мы получили модель новой числовой последовательности – геометрической прогрессии. Можем дать ее определение, записать формулу n-го члена, сформулировать характеристическое свойство. А можно ли получить формулу для вычисления суммы n-первых членов этой прогрессии? |
| Это и будет задачей нашего следующего урока. А дома предлагаю заполнить таблицу, которую мы начали на уроке. |
|
(На следующий урок учащиеся принесут таблицу, вид которой в приложении 6. Готовая таблица будет полезна на уроках преобразования моделей прогрессий.)
В заключение своей работы хочу сказать, что учебный процесс представляет собой сложную динамическую систему, в которой в органическом единстве осуществляется взаимная деятельность учителя (преподавание) и ученика (учение) Каждый из субъектов этого процесса имеет свои функции. Задача учителя состоит не только в том, чтобы сообщать знания, но и управлять процессом усвоения знаний и способов деятельности. Задача ученика – овладеть системой знаний, способами их получения, переработки, хранения, применения и воспитать в себе необходимые качества личности. Желание учиться, интерес к новым знаниям – характерная черта рода человеческого. Заметить и развить этот интерес довольно трудно: современная практика обучения «скучным» наукам весьма успешно «гасит» его. Но как только подлежащий усвоению материал возбуждает интерес ребенка, обучение становится привлекательным. Поэтому наибольшую ценность приобретает усвоенный учеником метод самостоятельного постижения темы, когда простое воспроизведение материала сменяется творческой переработкой усвоенных знаний, попыткой на практике продемонстрировать уровень собственных способностей.
Одним из путей достижения поставленной цели является использование мною в своей педагогической деятельности технологии развивающего обучения, который подразумевает учение через открытия, через решение проблемных ситуаций.
Учащиеся работающие по системе развивающего обучения, отличаются :
- культурой мышления (умением сопоставлять, оценивать, интерпретировать, систематизировать, осознавать и рефлексировать свои и чужие мысли и переживания);
- культурой деятельности (умением видеть и ставить цели, планировать, проектировать и анализировать ситуацию, осуществлять исследования и организационно-управленческую деятельность);
-культурой общения и речи (умением преобразовывать текст, формулировать сущностные определения, осуществлять цепь суждений, организовывать коллективную деятельность, изменять высказывания в зависимости от адресата);
- психологической и этической культурой (развитием воли, самонаблюдения, формированием самоанализа, самооценки, формированием установки на альтернативность, проблематизацию, доказательность).
-25-
-
Список литературы.
1 .Асташкина И. С., Бубличенко О. А. Дидактические материалы к урокам алгебры в 8-9 классах. Ростов-на-Дону, 2003г.
2. Бондаровская Е. В. Учителю о личностно-ориентированном образовании. Ростов-на-Дону, 1998г.
3. Воронцов А. Б. Практика развивающего обучения. М., «Русская энциклопедия», 1998г.
4. Григорьева Т. П., Иванова Т. А., Кузнецова Л. И., Перевозщикова Е. Н. Основы технологии развивающего обучения математике. Нижний Новгород, 1997г.
З.Давыдов В. В. Теория развивающего обучения. М., 1996г.
6. Игнатьева Г. А., Дмитриев В. В., Шишкина О. П. Преемственность в развивающем обучении. Нижний Новгород, 1997г.
7. Мордкович А. Г. Алгебра-9 Учебник, задачник. М., 2005г.
8. Мордкович А. Г. Алгебра 7-9 Методическое пособие для учителя. М., 2000г.
9. Педагогические идеи Л. В. Занкова и школьная практика. М., 2001г.
10. Эрдниев П. М. Преподавание математики в школе. М., 1978г.
11. ГИА по математике Учебно-тренировачные тесты и другие материалы для 9 класса, Москва, Санкт-Петербург,»Астрель – Спб», 2010г.
12. Мордкович А.Г., Тульчинская Е.Е.Алгебра Тесты для 7-9 классов общеобразовательных учреждений, Москва, «Мнемозина, 2000г.
13. Ю.П. Дудницын Алгебра 9 класс Контрольные работы под редакцией Мордковича А.Г. Москва, «Мнемозина, 2001г.
-38-
Приложение 7.
По горизонтали
1. Первый из двух стоящих рядом членов последовательности
2. Разность последовательно одинаковых членов
3. Способ задания последовательности
4. Число в арифметической прогрессии
5. Элементы, из которых состоит последовательность
6. Натуральное число, обозначающее место члена в последовательности
По вертикали
1. Функция, заданная на множестве натуральных чисел
7. Вид последовательности
8. Последовательность, содержащая конечное число членов
-32-
Приложение 8.
| № | вопрос | ответ |
| 1 | Функция, заданная на множестве натуральных чисел, называется | а) прогрессия б) последовательность в) уравнение |
| 2 | Формулу, выражающую любой член последовательности, начиная с некоторого, через предыдущие называют | а) записью б) рекуррентной в) функцией |
| 3 | Какой член последовательности следует за членом аn+1 | а) аn б) аn-1 в) аn+2 |
| 4 | (аn) – арифметическая прогрессия аn+1 = …+а вставьте пропущенное | а) аn-1 б) аn в) аn+2 |
| 5 | (а…) – арифметическая прогрессия. Запишите формулу n-го члена через а1 и d |
|
| 6 | Дано: :(аn) а1 = 20, d = 3 Найти: а5 | а) 12; б) 32; в) 25 г) др.ответ |
| 7 | Если а10 а11 а12 члены арифметической прогрессии, то запишите характеристическое свойство, т.е. выразите d11 через d11 и d12 |
|
| 8 | Найдите сумму первых восьми членов арифметической прогрессии, если а1 = -17 d=6 | а) 26; б) 32; в) 30 г) др.ответ |
| 9 | Найдите сумму нечетных натуральных чисел от 1 до 29 включительно | а) 725; б) 210; в) 200
|
| 10 | Найти сумму первых ста членов арифметической прогрессии аn = 2 n + 3 |
|
-33-
Приложение 9.
| № | вопрос | ответ |
| 1 | Последовательность (xn) задана формулой xn = 10n2 + 4. Найти x10 | а) 104; б) 204; в) 1004; г) др.ответ |
| 2 | Числовая последовательность задана формулой xn = 2n + 3. Найти номер члена последовательности, равного 43 | а) 23; б) 20; в) 21; г) др.ответ |
| 3 | Найти пятнадцатый член арифметической прогрессии 3; 7;… | а) 59; б) 98; в) 63; г) др.ответ |
| 4 | Запишите формулу члена арифметической прогрессии 1; 4; 7; 10;… | а) аn = n2; б) аn = 3n – 2; в) аn = 3n+1; г) др.ответ |
| 5 | Разность арифметической прогрессии равна 1,5. Найти а1, если а7 = -4. | А) -23; б) -60; в) -13; г) др.ответ |
| 6 | Число -28 является членом арифметической прогрессии (аn), у которой а1 = 32, а разность d = -1,5. Найти его номер. | А) 41; б) 33; в) 38; г) др.ответ |
| 7 | В арифметической прогрессии (аn) а1 = 8, d = 4. Найти сумму шестнадцати членов прогрессии. | А) 720; б) 608; в) 594; г) др.ответ |
| 8 | Найти сумму всех натуральных чисел от 2 до 98 включительно. | А) 5050; б) 4500; в) 4850; г) др.ответ |
| 9 | Арифметическая прогрессия задана формулой аn = 3n + 2. Найти сумму двадцати первых членов. | А) 670; б) 630; в) 400; г) др.ответ |
| 10 | Известны два члена арифметической прогрессии (аn) а5 = 8,2 и а10 = 4,7. Укажите число положительных членов прогрессии. | А) 21; б) 15; в) 16; г) др.ответ |
| № | вопрос | ответ |
| 1 | Последовательность (xn) задана формулой xn = 2n-1. Найти x20. | А) 19; б) 39; в) 29; г) др. ответ |
| 2 | Числовая последовательность задана формулой xn = n2 -1. Найти номер члена последовательности, равного 224 | а) 10; б) 15; в) 25; г) др. ответ |
| 3 | Найти десятый член арифметической прогрессии 4; 9;… | а) 45; б) 49; в) 40; г) др.ответ |
| 4 | Запишите общую формулу арифметической прогрессии 1; 5; 9; 13;… | а) 4n+1; б) 4n-1; в) 4n-3; г) др.ответ |
| 5 | Разность арифметической прогрессии равна 2. Найти а1, если а6 = -3. | А) 10; б) -13; в) 13; г) др.ответ |
| 6 | Число -20 является членом арифметической прогрессии, у которой а1 = -31, а разность равна 3. Найти его номер. | А) 6; б) 7; в) 10; г) др.ответ |
| 7 | В арифметической прогрессии (аn) а1 = 5, d = 3. Найти сумму первых двадцати членов арифметической прогрессии. | А) 640; б) 570; в) 670; г) др.ответ |
| 8 | Найти сумму всех натуральных чисел от 5 до 95 включительно. | А) 4550; б) 5050; в) 4050; г) др.ответ |
| 9 | Арифметическая прогрессия задана формулой аn = 5n – 1. Найти сумму пятнадцати первых членов прогрессии. | А) 370; б) 375; в) 485; г) др.ответ |
| 10 | Известны два члена арифметической прогрессии а8 = -10 и а11 = -25. Укажите число положительных членов арифметической прогрессии. | А) 5; б) 6; в) 8; г) др.ответ |
-34-
Приложение 10.
|
| вопрос | ответ |
| 1 | Последовательность задана рекуррентной формулой аn+1 равно корень квадратный из аn и условием а1 = 256. Найти четвертый член последовательности. | а) 16; б) 8; в) 2; г) др.ответ |
| 2 | Числовая последовательность задана формулой аn = n2 -2n-6. Найти номер члена последовательности, равного 9. | а) 4; б) 5; в) 8; г) др.ответ |
| 3 | Найти разность арифметической прогрессии, если первый член равен -4, а девятый член прогрессии равен 0. | а) 0,5; б) 1; в) 2; г) др.ответ |
| 4 | Запишите формулу общего члена арифметической прогрессии 2; 6;… | а) аn = n2+n; б) аn = 4n-2; в) аn = 4n+2; г) др.ответ |
| 5 | Число -59 является членом арифметической прогрессии 1; -5;… | а) 13; б) 19; в) 11; г) др.ответ |
| 6 | Найти девятый член и разность арифметической прогрессии, если а8 = 126, а10 = 146. | а) d=10, а9=136; б) d=8, а9=134; в) d=5, а9=131; г) др.ответ |
| 7 | Найти сумму двадцати пяти первых членов арифметической прогрессии (аn), если а1=66 и d = -8 | а) -680; б) 680; в) -750; г) др.ответ |
| 8 | Найти сумму всех четных двузначных чисел. | а) 2408; б) 2450; в) 2440; г) др.ответ |
| 9 | Найти сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3. | а) 1192; б) 2038 в) 1234; г) др.ответ |
| 10 | Найти сумму первых двадцати членов арифметической прогрессии, если ее четвертый член равен 3, а шестой равен -1,2. | а) -31; б) -27; в) -26; г) др.ответ |
-35-
Приложение 11.
1.В арифметической прогрессии a5 = 8,7 и a8 =12,3.Найдите d и a1
a)d=l,6 и a1 = 2,3; б) d=3,6 и a1=-5,7; в) d=l,2 и a1=3,9; r)d=l,4 и a1=3,l.
2. В арифметической прогрессии a1=-5,6 и а2=-4,8. На каком месте
(укажите номер) находится число 16?
А)n=14; б)n=13; в) n=27; г) n=28.
3. В арифметической прогрессии a1=29,2 и а2=27,9. На каком месте
(укажите номер) стоит первое отрицательное число? Найдите это число.
А) -1,1; б) -0,9; в) -0,7; г) -0,3.
4. Найдите сумму первых восемнадцати членов арифметической
прогрессии, заданной формулой аn=4n+9.
А) 732; б) 846; в) 768; г) 934.
5. В геометрической прогрессии , . Найдите знаменатель q.
А) 2; б) ; в) или ; г) .
6. В геометрической прогрессии a1=, 0, a2=. Найдите пятый член этой
прогрессии.
А)
7. В геометрической прогрессии . Найдите сумму шести первых членов этой прогрессии.
А) -9,3; б) 6,3; в) 3,2; г) -18,9.
8. Найдите первый член арифметической прогрессии, если a1+a6=26 и
а2+а3=18. А) 3; б) 2; в) 4; г) 1,5.
9. Для периодической дроби 0,58(3) найдите несократимую
обыкновенную дробь. Запишите разность числителя и знаменателя.
А) 3; б) 7; в) 5; г) 2.
10. Дано: (bn) –геометрическая прогрессия, b1=2, q=3. Какой цифрой
оканчивается b15?
А) 6; б) 8; в) 4; г) 2.
-36-
Приложение 12.
Карточки готовит учитель разного уровня и учащиеся сразу знают на какую максимальную оценку они работают. Карточки заготовить в достаточном количестве, чтобы удовлетворить желания всех учащихся, решать на определенную оценку.
Оценка «3»:
| 1. Найдите  и и  для геометрической прогрессии для геометрической прогрессии  , у которой , у которой  . . | 2. Найдите  и и  для геометрической прогрессии для геометрической прогрессии  , у которой , у которой  . . |
| 3. Найдите пятый член геометрической прогрессии  , если , если  . . | 4. Найдите седьмой член геометрической прогрессии  , если , если  . . |
| 5. Является ли число А = 64 членом геометрической прогрессии 0,5; 1; …? Если да, то укажите его номер. | 6. Является ли число А =  членом геометрической прогрессии 3; 1; …? Если да, то укажите его номер. членом геометрической прогрессии 3; 1; …? Если да, то укажите его номер. |
| 7. Найдите четвертый член геометрической прогрессии
8, -4, … | 8. Найдите пятый член геометрической прогрессии
10, -5, … |
| 9. Дана геометрическая прогрессия 8, -4, … . Найдите номер члена этой прогрессии, равного  . . | 10. Дана геометрическая прогрессия 10, -5, … . Найдите номер члена этой прогрессии, равного 0,1. |
Оценка «4»:
| 1. Дана геометрическая прогрессия  . Найдите . Найдите  , если , если  . . | 2. Дана геометрическая прогрессия  . Найдите . Найдите  , если , если  . . |
| 3. Найдите такие значения переменной  , при которых числа , при которых числа  образуют геометрическую прогрессию. образуют геометрическую прогрессию. | 4. Найдите такие значения переменной  , при которых числа , при которых числа  образуют геометрическую прогрессию. образуют геометрическую прогрессию. |
| 5. Найдите сумму первых десяти членов геометрической прогрессии, заданной формулой  . . | 6. Найдите сумму первых четырех членов геометрической прогрессии, заданной формулой  . . |
| 7.Сколько членов геометрической прогрессии 18, -6, … больше числа 0,01? | 8.Сколько членов геометрической прогрессии 18, -6, … меньше числа -0,01? |
Оценка «5» ставится тем учащимся, кто уже справился с несколькими заданиями на оценку «4» и решил карточку на оценку «5»:
| 1. Найдите сумму четвертого, пятого, шестого и седьмого членов геометрической прогрессии 32, 16, … . | 2. Найдите сумму третьего, четвертого, пятого и шестого членов геометрической прогрессии  . . |
| 3. Сумма второго и третьего членов геометрической прогрессии равна 6, а знаменатель прогрессии равен 2. Найдите первый член прогрессии. | 4.Сумма второго и четвертого членов геометрической прогрессии равна 120, а знаменатель прогрессии равен 2. Найдите первый член прогрессии. |
| 5. Разность между вторым и первым членами геометрической прогрессии равна -3, а разность между третьим и вторым ее членами равна -6. Чему равна сумма первых пяти членов прогрессии? | 6. Разность между вторым и первым членами геометрической прогрессии равна -1, а разность между вторым и третьим ее членами равна 4. Чему равна сумма первых шести членов прогрессии? |







 n+1 = an + d
n+1 = an + d апишите эту последовательность с помощью таблицы.
апишите эту последовательность с помощью таблицы.



















