Россия, село Новый Артаул
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 29.04.2020 06:17
Гильмутдинова Люзия Сахабиевна
Учитель математики
62 года
328
126 574 
Местоположение
Специализация
Методическая разработка урока алгебры в 8 классе «Способы решения квадратных уравнений»
Категория:
Математика
10.01.2020 20:06
Просмотр содержимого документа
«Методическая разработка урока алгебры в 8 классе «Способы решения квадратных уравнений»»
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа с.Новый Артаул
Муниципального района Янаульский район Республики Башкортостан
8 класс
Методическая разработка урока
по алгебре
«Способы решения квадратных уравнений»
Выполнила учитель математики
Гильмутдинова Л.С.
Оглавление
Обоснование выбора, методы обучения на уроке, актуальность поставленной цели
Место урока в тематическом планировании и системе уроков
Организация учебной деятельности с учётом личностно – ориентированной технологии обучения
Организация учебной деятельности с учётом здоровье сберегающей технологии обучения
Организация учебной деятельности с учётом ИКТ
Цель урока
Ход урока
Конспект урока
Самоанализ урока
Приложение
Литература
Обоснование выбора
Мир не стоит на месте. Учителя тоже. Перед ним стоит задача мотивировать детей на активную работу на уроке, чтобы им было не скучно, а увлекательно и интересно. Есть много технологий, методов обучения и форм проведения урока. Одной из таких форм является урок – обобщения и систематизации знаний, на котором обучающиеся сами находят способы решения квадратных уравнений, обсуждают их решение, учатся критически мыслить, анализировать.
Методы обучения на уроке:
информационные методы - использование презентации Power Point;
методы педагогики – методы организации и стимулирования учебной деятельности;
математические методы – использование математического языка, моделирование;
методы психологии – развитие мыслительных операций: анализ и синтез, классификация и систематизация, сравнение и обобщение
Актуальность поставленной цели урока
При решении квадратных уравнений обучающимися одним из способов использования является нахождение дискриминанта. Другие способы обычно применяют 10-20 % детей. Данный урок - урок обобщения и рассмотрения различных способов решения квадратных уравнений, изучаемых на уроках алгебры в разное учебное время; привести усвоенные способы в стройную систему. Конечным результатом усвоения таких систем знаний является сознательное овладение основными способами решения квадратных уравнений.
Место урока в тематическом планировании и системе уроков
Преподавание ведётся по учебнику «Алгебра - 8», под редакцией С.А. Теляковского. Темы учебника «Решение квадратных уравнений выделением квадрата двучлена», «Решение квадратных уравнений по формуле», «Теорема Виета», «Графический способ решения уравнений» уже изучены. Текущий урок позволяет обобщить все ранее изученные способы, так как к его проведению они умеют решать уравнения различными методами. Есть ещё тема: «График квадратичной функции», которая будет рассмотрена в 9 классе.
Форма организации деятельности учащихся
На уроке я использую технологию индивидуально-группового обучения. Индивидуальная, парная, групповая работа. Организация индивидуальной деятельности позволяет учитывать способности и образовательные потребности каждого, а коллективная (командная, бригадная) деятельность оказывает помощь каждому обучающемуся в успешном освоении учебной программы. Нa дaнном урoке обучающиеся разбиваются на группы по принципу личных симпатий для коллективной работы. Начало выполнения задания происходит путём «мозгового штурма», когда каждый по очереди высказывает свою мысль. В каждой группе есть 2 человека, которые «собирают» лучшие идеи, 1 человек в каждой группе записывает решение. Ребята в группе работают так, чтобы каждый смог затем решить уравнение этим способом, рассказать решение у доски. Если кому-то не понятно, то ему индивидуально более сильный обучающийся объясняет еще раз. Назначается ассистент от каждой группы, и он оглашает результат работы группы, защищает решение у доски.
Организация учебной деятельности с учётом личностно - ориентированной технологии
На уроке созданы условия для реализации основных принципов личностно ориентированной технологии обучения. Это выражено в следующем:
оценка деятельности обучающийсяа не только по конечному результату (правильно, неправильно), но и по процессу его достижения;
создание атмосферы взаимной заинтересованности в работе учащихся и учителя;
создание обстановки для естественного самовыражения обучающийсяа;
стимулирование учащихся к высказываниям, использованию различных способов решения задачи без боязни ошибиться, получить неправильный ответ;
поощрение стремления обучающийсяа находить свой способ решения задачи, анализировать способы других обучающийсяов в ходе урока, выбирать и осваивать наиболее рациональные;
создание педагогических ситуаций межгруппового и внутригруппового общения на уроке, позволяющих каждому обучающийсяу проявлять инициативу, самостоятельность, избирательность в способах работы;
создание ситуации выбора и успеха;
создание условий для актуализации и обогащения субъектного опыта учащихся
Организация учебной деятельности с учётом здоровье сберегающей технологии обучения
Учебная деятельность, организованная на уроке, способствует сохранению здоровья детей, а именно:
своевременная подготовка к уроку и его мобилизующее начало;
доброжелательная атмосфера, способствующая положительному эмоциональному настрою;
чёткая организация учебного труда;
групповая работа, создающая ситуацию, когда «трудноусваиващий» обучающийся, чувствует поддержку товарища;
объединение в группы по желанию обучающихся, то есть с учетом психологической совместимости;
антистрессовые моменты, выраженные в стимулировании обучающихся к нахождению различных по содержанию способов решения квадратных уравнений, без боязни ошибиться;
смена видов деятельности обучающихся;
физкультминутка, выполнение упражнений для глаз для снятия усталости.
Организация учебной деятельности с учётом ИКТ.
Презентация Power Point используется на данном уроке в качестве демонстрации. Презентация состоит из 14 слайдов, включая титульный лист. Использование таблиц, формул, картинок на слайдах позволяет обучающимся не терять время на обдумывание вопросов и решения уравнения данным способом. Экономит время.
Оформление презентации отвечает основным требованиям:
один и тот же вид информации помещён в одном и том же месте;
в центре слайдов помещена основная текстовая информация, которой обучающиеся должны пользоваться при решении квадратных уравнений;
тексты заданий помещены в верхней части слайдов;
при оформлении презентации минимизировано количество используемых цветов, для выделения наиболее важных данных и развития зрительной памяти использован один и тот же цвет;
разумно использован цветовой контраст.
Использование ИКТ на данном уроке способствует:
повышению познавательной активности обучающихся: развивается интерес к теме, каждый обучающийся на уроке занят делом, никто не бездельничает;
решению всех задач урока: обучающих, развивающих, воспитательных;
повышению интенсификации урока и темпа урока: презентация позволила значительно сократить время на обдумывание решения;
увеличению объёма выполненной работы.
ИКТ выполняет важные функции и в деятельности учителя на уроке, увеличивая его возможности в качестве воспитателя, организатора, оценивающего и контролирующего процесс и результаты обучения.
Результат деятельности обучающихся.
Результатом деятельности обучающихся на уроке является понимание сути различных способов решения квадратных уравнений, осознанный и вдумчивый подход к анализу, поиску новых способов. Открытия для себя нового, осознание чувства сопричастности к общему успеху.
Цель урока: Обобщение темы: «Квадратное уравнение»; создание условий для осознанного и уверенного владения навыком решения квадратных уравнений, рассмотрение различных способов решения квадратных уравнений.
Образовательные задачи урока: систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений, расширить и углубить представления обучающихся о решении уравнений, организовать поисковую деятельность обучающихся при решении квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки; навыки самостоятельной работы;
развивать устную и письменную речь обучающихся;
привить любовь к предмету, желание познать новое.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать потребность добиваться успехов в приобретении знаний; воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.
Формы обучения: Индивидуальная, фронтальная работа, парная работа, взаимопомощь, групповая деятельность.
Тип урока: Урок обобщения и систематизации знаний.
Оборудование: Мультимедийная установка, кoмпьютер, презентация, листы учета знаний, карточки
Ход урока 45 мин
| № п/п | Структура и содержание | Методы и приемы | Время |
| 1 | Введение. Организационный момент. Предъявление темы и постановка задач урока | Рассказ
| 2 мин
|
| 2 | Обобщение, систематизация знаний. Устная работа. Фронтальный опрос. Выполнение заданий. Работа в тетради Работа в группах. Защита у доски Физкультминутка.
Объяснение.
| Объяснительно-иллюстр. метод Беседа Репродуктивный метод, самоконтроль Частично – поисковый метод Исследовательский метод Коллективный поиск Рассказ учителя
| 3 мин 10мин 5 мин 10 мин 1 мин 5 мин 2 мин 4 мин
|
| 3 | Домашнее задание | Инструктаж учителя |
|
| 4 | Итог урока. Рефлексия | Синквейн | 3 мин |
Конспект урока
| Действие учителя | Действие обучающихся |
| I. Введение. Организационный момент. Презентация. Слайд № 2.
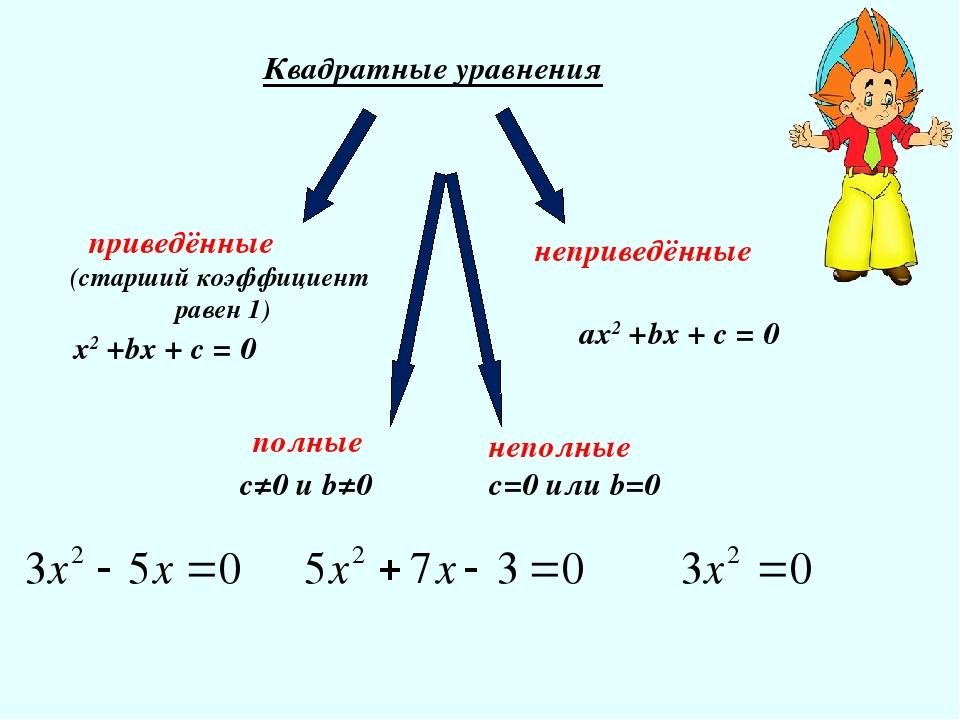
Краткий рассказ про квадратные уравнения
Слайд № 3. Цели урока: 1. образовательная – формирование умения систематизировать и ориентироваться в полученных знаниях, свободно владеть ими. 2. воспитательная – формирование навыков самоконтроля и взаимоконтроля. 3. развивающая – развитие внимания, памяти, познавательного интереса к предмету, умения рассуждать и аргументировать свои действия.
2.Обобщение и систематизация знаний. Перед вами 4 уравнения. --Какие из приведенных ниже квадратных уравнений можно решить сейчас? (Все, кроме последнего примера). 2. 5 3. 7 4. -- Что объединяет те квадратные уравнения, которые можно решить прямо сейчас? (Они являются неполными квадратными уравнениями). Давайте решим такие уравнения.
Ответы: 1) х=5; -5. 2) х= 0; 1 3) корней нет. Фронтальный опрос Слайд №4,5
Сформулируйте определение квадратного уравнения. (Квадратным уравнением называется уравнение вида Назовите формулы неполных квадратных уравнений. Почему они называются неполными квадратными уравнениями? (Формулы неполных квадратных уравнений: Как взаимосвязаны дискриминант и корни квадратного уравнения? Чему равны корни квадратного уравнения? (При вычислении корней квадратного уравнения необходимо знание дискриминанта: Х=
Решение уравнений. Один обучающийся, решая квадратное уравнение
Решение: Первая ошибка допущена при вычислении дискриминанта: D= Вторая ошибка допущена при вычислении первого корня уравнения. При D= 4,
Выполнение заданий.
Упрощенные задания. А) 4 Решение: 4 Ответ, данный в задании, верный. Б) 5 Решение: 5 Ответ, данный в задании, не верный. Ответ: х=0. Задания для среднего уровня. А) Решение: Ответ, данный в задании, не совсем верный. Ответ: х=±1. Б ) Решение:
Корней нет. Ответ, данный в задании, неверный. Ответ: корней нет. Задания повышенной сложности. А) Решение: x=0 или 3х+1 =0, x=0 или 3х= -1, x=0 или х= - Ответ, данный в задании, неверный. Ответ: Б) Решение: 9 x=0 или 3х-2=0, x=0 или 3х=2, x=0 или х= Ответ, данный в задании, не совсем верный. Ответ:
Работа в группах. На листочках написан способ, которым вы должны решить квадратное уравнение и затем защитить своё решение:
- Сегодня мы с вами решим одно квадратное уравнение 3х2 +2х-1=0 и постараемся вспомнить все способы, которые мы уже знаем. Слайд №6 1 способ: «По общей формуле, через дискриминант». Используя общую формулу корней квадратного уравнения, решите его.
Обучающиеся решают в тетради:
Способ № 2. «Разложение левой части уравнения на множители способом группировки».
3х2+2х-1=0, Представим слагаемое 2х в виде разности 3х-х. Разложим левую часть на множители: 3х2+2х-1= 3х2+3х-х-1= 3х(х+1)+(-х-1)= 3х(х+1)-1(х+1)=(х+1)(3х-1) Следовательно, уравнение можно записать так: (х+1)(3х-1)=0, Произведение равно нулю, если хотя бы один из множителей равен нулю, а другой при этом определен. х+1=0 или 3х-1=0, х=-1. 3х=1, х= Левая часть уравнения обращается в нуль при х=-1;х=
Способ № 3. «По сумме коэффициентов квадратного уравнения»
Если в квадратном уравнении ах2+вх+с=0, сумма коэффициентов а-в+с=0, то х1=-1, х2= 3х2+2х-1=0, а=3,в=2,с= -1, а-в+с=3-2+(-1)=0, значит х1=-1, х2= Ответ: – 1; Физкультминутка Вверх рука и вниз рука. Способ №4. Графический способ решения.
Слайд №7
3х2+2х-1=0. В уравнении второй и третий член перенесем в правую часть, то получим 3х2 =-2х+1.Построим графики зависимостей у=3х2 и у=-2х+1. График первой зависимости -парабола, проходящая через начало координат. Так как коэффициент равен 3, то ветви параболы направлены вверх. График второй зависимости – прямая. Прямая и парабола пересекаются в двух точках А и В. С абсциссами х1=-1 и х2= Мы убедились, что пути решения даже одной и той же задачи могут быть очень разнообразными. 3.Домашнее задание
4.Итог урока.
Выставление оценок Слайд №8
Сейчас давайте подведем итоги нашего урока при помощи синквейна. Слайд №9,10.
Работаем группами, вам надо составить синквейн на тему: урок, уравнение, работа в группе, способы, восьмиклассники.
Вашим девизом, после этого урока должны стать слова: «Научился сам, научи - другого!» Слайд №1 Я хочу закончить наш урок словами французского писателя Эмиля Золя «Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать больше». |
Внимательно слушают
Обучающиеся решают уравнения. Они не поясняют ход своего решения. Просто дают готовый ответ
Обучающиеся поочередно отвечают на поставленные вопросы. Каждый обучающийся может ответить только один раз.
Обучающиеся пишут в тетради. Затем один обучающийся выходит к доске и исправляет ошибки.
Обучающиеся вытягивают листы. Группой работают в тетрадях. Объясняют, проговаривают друг другу. Выбирают выступающего, Чтобы рассказать, как решать квадратное уравнение.
Идет защита, остальные обучающиеся пишут с доски в тетрадь.
выполняют движения за учителем
Обучающиеся смотрят на слайд № 7
Обучающиеся пишут в дневник.
Обучающиеся составляют, а потом зачитывают:
Урок Необычный, увлекательный Думаем, решаем, общаемся Я умею решать уравнения Интересно Работа в группе Весело, увлекательно Решать, обсуждать, помогать Мне нравится так учиться Мы вместе Рисуют в листах учета свои эмоции: ☺ Сдают листы учета знаний учителю. |
- 25 = 0
- 5х = 0
+ 7 =0
+вх + с =0, где а,в,с – заданные числа, а≠ 0, х – неизвестное).
, 
называется приведенным квадратным уравнением? (Квадратное уравнение 
называется приведенным, если первый коэффициент равен 1).
- 4ас =100-96=4;
=
=
=
.
=-8, 
=-6.
-4ас = 100+ 96=196.
=
.
=а (4а =1)
.
.
- 3х +25+3х=0;
(х(3х)=0)
.
- 1=0.(х=0)
.
.
.
=
Самоанализ урока
Урок по теме: «Способы решения квадратных уравнений» проведен в 8 классе.
Образовательные задачи урока:
систематизировать знания, выработать умение выбирать рациональный способ решения квадратных уравнений, расширить и углубить представления обучающихся о решении уравнений, организовать поисковую деятельность обучающихся при решении квадратных уравнений и создать условия контроля (самоконтроля, взаимоконтроля) усвоения знаний и умений.
Развивающие задачи урока:
развивать математическое мышление, память, внимание;
развивать умение анализировать, сравнивать, обобщать, классифицировать, строить умозаключения, делать выводы;
развивать коммуникативные навыки; навыки самостоятельной работы;
развивать устную и письменную речь обучающихся;
привить любовь к предмету, желание познать новое.
Воспитательные задачи урока:
воспитывать культуру умственного труда;
воспитывать культуру коллективной работы;
воспитывать информационную культуру;
воспитывать потребность добиваться успехов в приобретении знаний;
воспитание навыков самоконтроля и взаимоконтроля, развитие самостоятельности и творчества.
В данном коллективе обучаются дети с хорошими и средними способностями. Урок – обобщения и систематизации знаний, на котором школьники сами находят способы решения квадратных уравнений, обсуждают их решение, учатся критически мыслить, анализировать, тесно связан с предыдущими уроками и опирается на знания ранее проведенных уроков. Данная тема является важной при изучении квадратичных функций, является необходимой при подготовке к сдаче ЕГЭ и ГИА по математике.
При планировании урока были учтены индивидуальные способности каждого.
Для создания эмоциональной атмосферы, заинтересованности, без которой невозможно формирование интереса к предмету необычно использовала четверостишье в начале урока и высказывания французского писателя Эмиля Золя в конце урока. Этот методический прием, безусловно, способствует концентрации внимания и повышает уровень усвоения материала.
Во избежание перегрузки и утомляемости обучающихся использовала различные виды контроля, проводила чередование видов деятельности:
а) фронтальный опрос;
б) карточки;
в) работа в группах;
Разнообразие видов деятельности, сочетание мыслительных и практических действий позволило поддерживать работоспособность обучающихся и мотивацию деятельности в активном состоянии на протяжении всего урока.
Организация индивидуальной деятельности позволила учесть способности и образовательные потребности каждого, а коллективная (командная, бригадная) деятельность оказывала помощь каждому учащемуся в успешном освоении учебной программы. На данном уроке обучающиеся разбивались на группы по принципу личных симпатий для коллективной работы.
Задания составлены доступные, ориентированы на выделение и усвоение главных элементов учебного материала.
При планировании каждого этапа учитывала дидактические задачи: учебное содержание, организацию деятельности обучающихся, методы обучения, реальный результат.
Для повышения качества и эффективности обучения максимально использую возможности кабинета. На данном уроке мною были использованы ТСО, таблицы, карточки, учебник.
Все это позволяет проводить урок четко, организованно и выполнять на уроках большой объем работы.
Урок цели достиг, были решены поставленные задачи обучающего характера
Приложение.
Лист учета знаний. 8 класс
| Фамилия | Имя |
|
|
|
| Способы решения квадратных уравнений | |||||
| | | | Защита | Самооценка | Итог |
|
|
|
|
|
|
|
Список использованной литературы:
1. Алгебра. Учебник для 8 класса общеобразовательных учреждений под редакцией С. А. Теляковского. – М.: Просвещение, 2007.
2. В.И. Жохов, Ю. Н. Макарычев, Н.Г. Миндюк. Дидактические материалы по алгебре для 8 класса. – М.: Просвещение, 2001.
3. Ковалева Г. И. Уроки математики в 8 классе. Поурочные планы. Часть 2.- Волгоград: Гринина Е. С.,2003.-64с.
4. Н.Л.Барсукова Открытые уроки алгебры. 7-8 классы; Москва; ВАКО; 2010г.
2020
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
