Методическая разработка урока статистики в 10-ом классе на тему:
«Число сочетаний»
ТИП УРОКА: изучение нового материала.
ЦЕЛЬ:
Ввести понятие «сочетания без повторений»
Провести сравнительный анализ перестановок, размещений, сочетаний
Познакомить учащихся с формулой и рассмотреть задачи, при которых она используется
ЗАДАЧИ:
Способствовать запоминанию основной терминологии, умению устанавливать события вероятности и вычислять перестановки и размещения;
Способствовать развитию интереса к математике; умений применять новый материал на практике и в жизни
Способствовать воспитанию аккуратности;
ОБОРУДОВАНИЕ: интерактивная доска, компьютер, презентация
ПЛАН УРОКА:
Организационный момент.
Устный счёт.
Актуализация опорных знаний.
Объяснение нового материала.
Обобщение знаний.
Первичное осмысление и закрепление.
Самостоятельная работа.
Подведение итогов урока, выставление оценок.
Ход урока
Организационный момент
Устный счёт.
Вычислите: 2!, 3!, 4!, 5!, 6!
2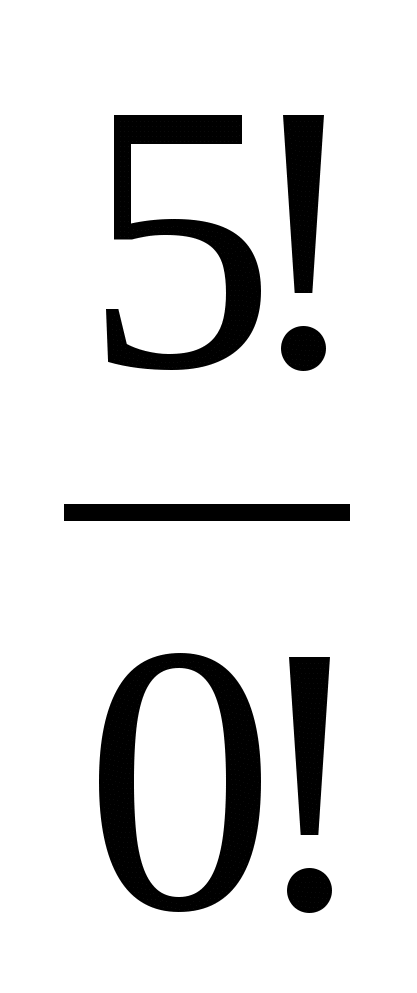
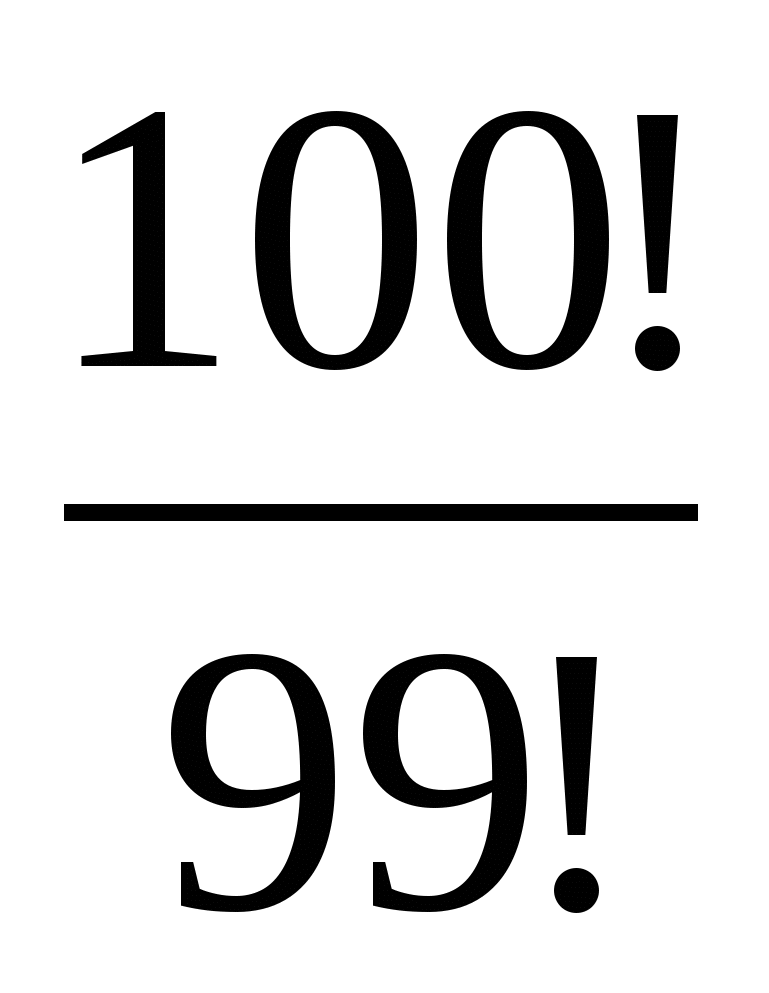
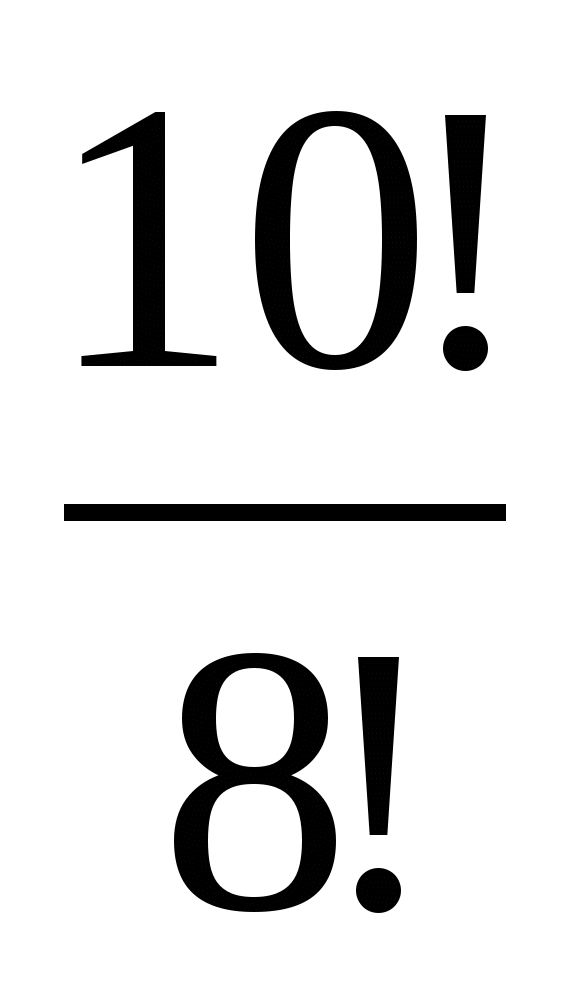
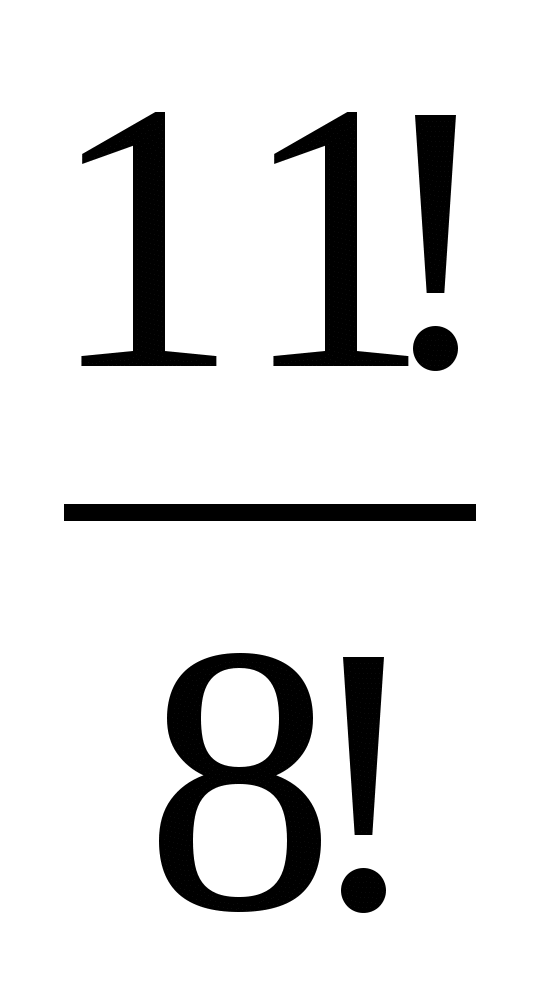 ) 3) 4)
) 3) 4)
Актуализация опорных знаний (повторение основных понятий и формул). Перестановки - выборки из n элементов, которые отличаются друг от друга только порядком расположения.
Формула Рn=n!
Размещения - выборки из n элементов по k , которые отличаются и составом и порядком расположения этих элементов.
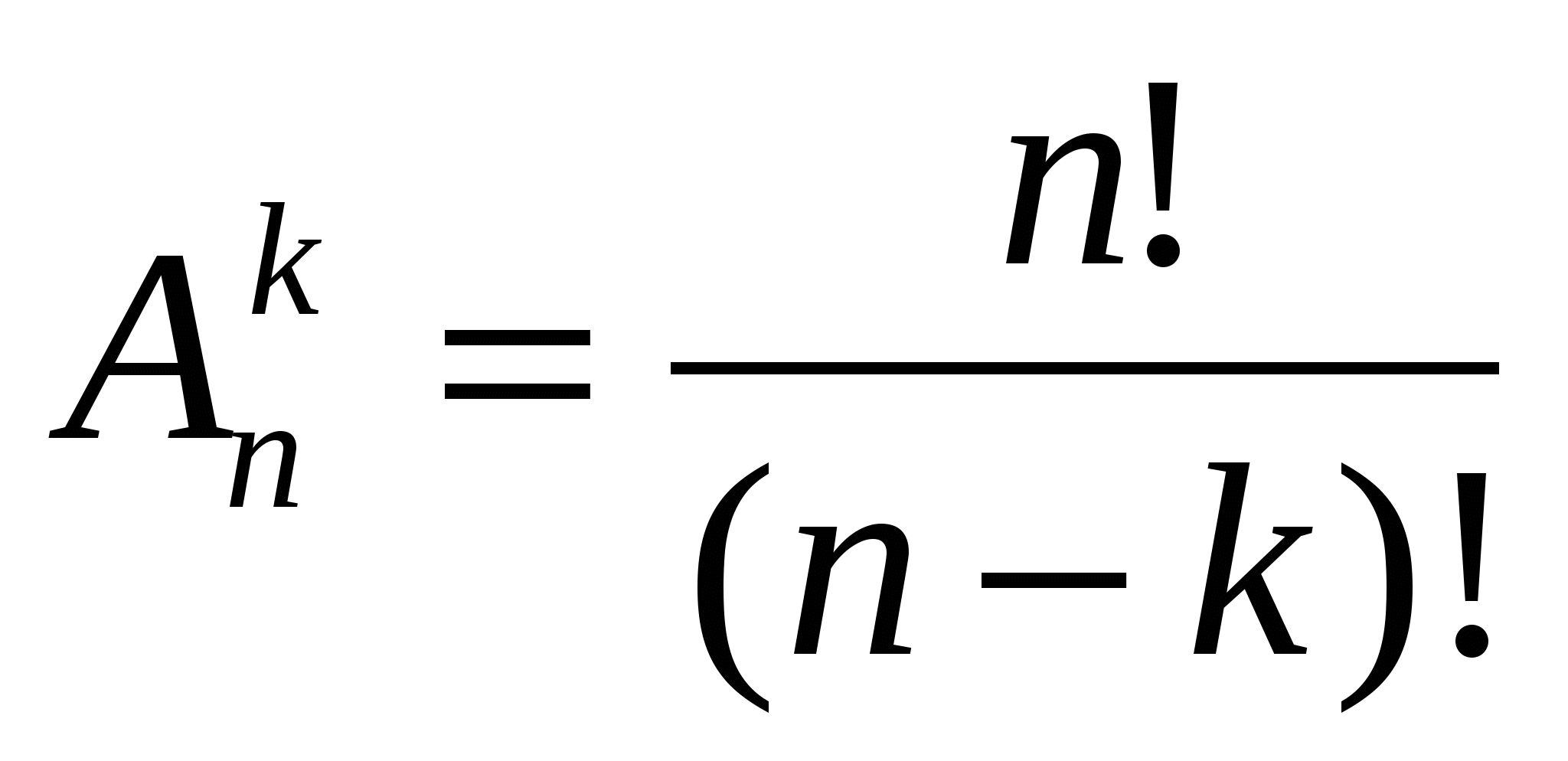
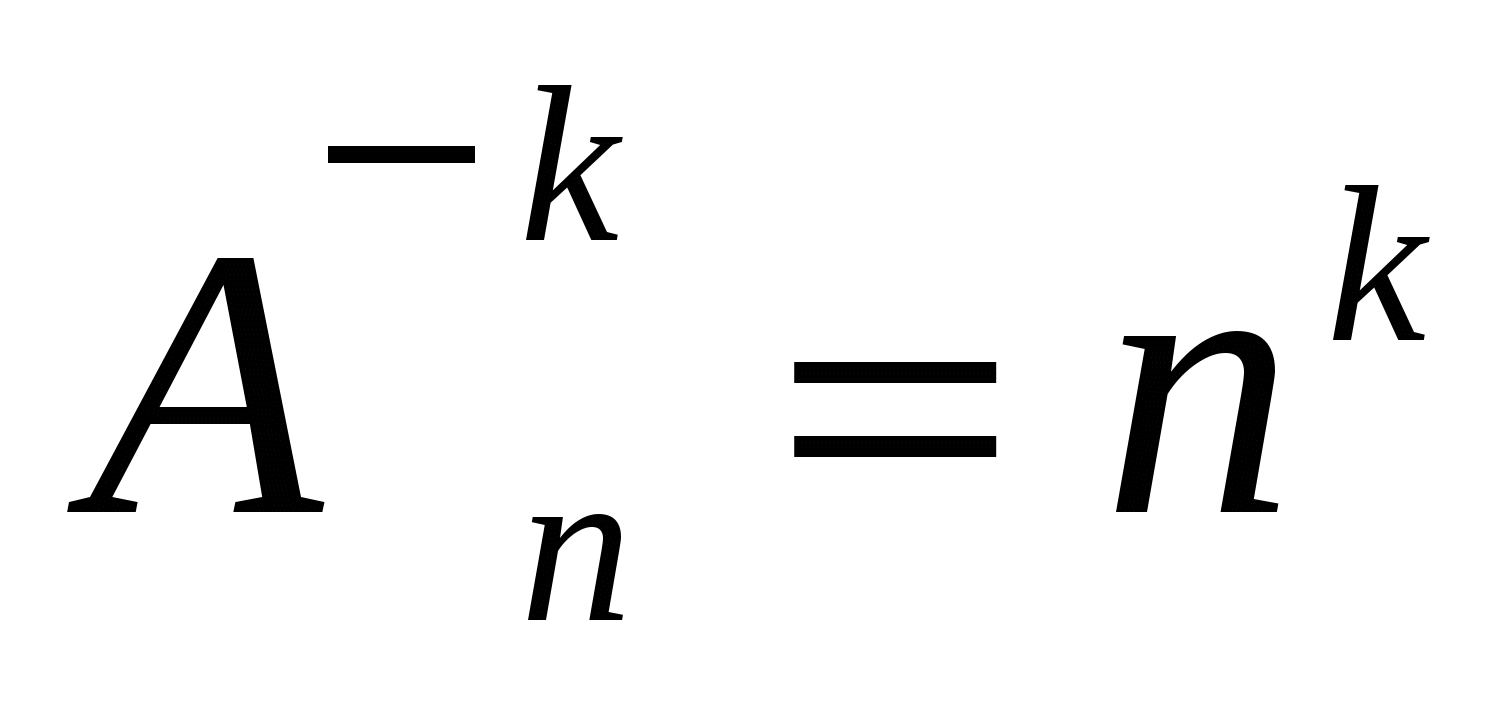
Изучение нового материала.
Еще в доисторическую эпоху люди сталкивались с комбинаторными задачами. Выбирать и расположить предметы в определенном порядке, отыскивать среди разных расположений наилучшее – вот задачи, решаемые в быту, на охоте или в сражениях. Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Нидийцы умели вычислять числа, которые сейчас называют "сочетания". В XII в. Бхаскара вычислял некоторые виды сочетаний и перестановок. Предполагают, что индийские ученые изучали соединения в связи с применением их в поэтике, науке о структуре стиха и поэтических произведениях. Например, в связи с подсчетом возможных сочетаний ударных (долгих) и безударных (кратких) слогов стопы из n слогов. По мере усложнения производственных и общественных отношений задачи усложнялись. Комбинаторные задачи встречались, как игры в досуге. Наряду с состязаниями в беге, метании диска, кулачными боями появлялись игры, требовавшие умение мыслить, рассчитывать, составлять планы, опровергать планы противника. Со временем игры усложнились: появились нарды, карты, шашки и шахматы. В таких играх приходилось рассчитывать различные ситуации, комбинации сочетания фигур.
В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов во множестве. Важно лишь то, какие именно элементы составляют множество.
К примеру, имеются пять гвоздик разного цвета. Обозначим их буквами a,b,c,d,e. Требуется составить букет из трёх гвоздик. Выясним, какие букеты могут быть составлены.
Если в букет входит гвоздика a, то можно составить такие букеты:
abc, abd, abe, acd, ace, ade.
Если в букет не входит гвоздика а, но входит гвоздика b, то можно получить такие букеты:
bcd, bce, bde.
Если в букет не входит ни гвоздика а, ни гвоздика b, то возможен только один вариант составления букета:
сde.
Определение. Сочетаниям из n элементов по k называется любое множество, составленное из k, элементов, выбранных из данных n элементов.
Число сочетаний из n элементов по k, обозначают (читается «С из n по k»).
В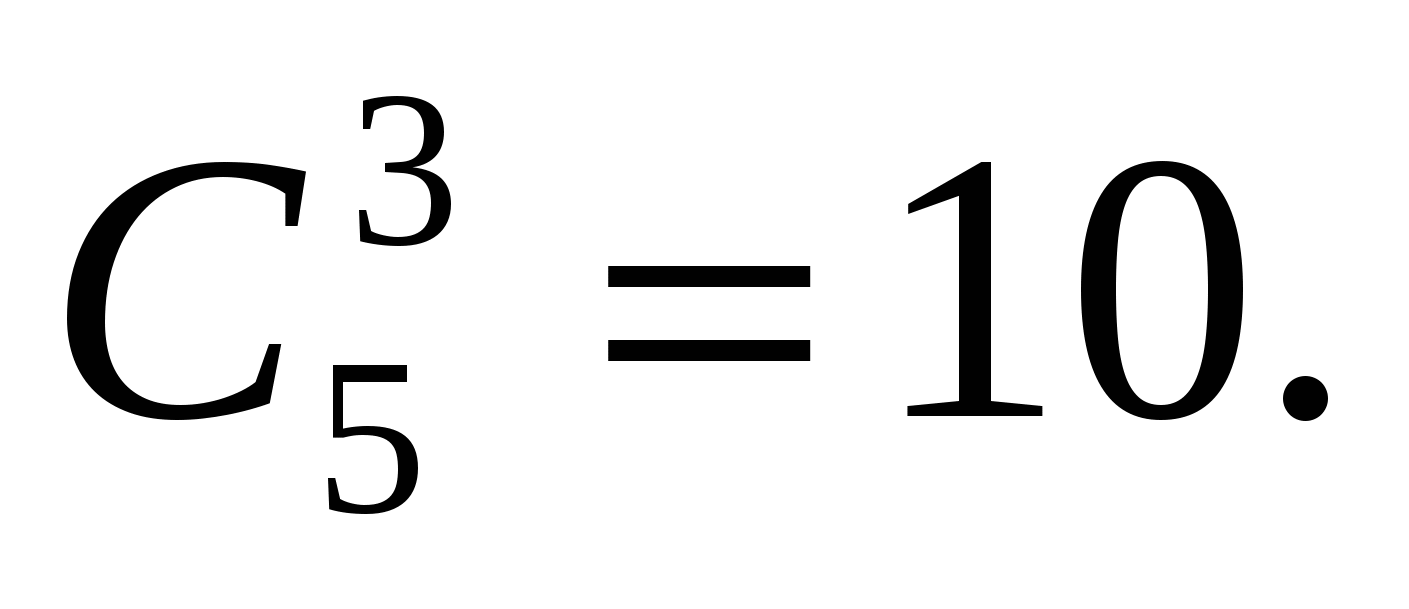 рассмотренном примере, составив все сочетания из 5 элементов по 3, мы нашли, что
рассмотренном примере, составив все сочетания из 5 элементов по 3, мы нашли, что
Вы
 ведем формулу числа сочетаний из n элементов по k, где k≤n .
ведем формулу числа сочетаний из n элементов по k, где k≤n .
Выясним сначала, как выражается через и Р3. Мы нашли, что из 5 элементов можно составить следующие сочетания по 3 элемента:
abc, abd, abe, acd, ace, ade, bcd, bce, bde, сde.
В каждом сочетании выполним все перестановки. Число перестановок из 3 элементов равно Р3. В результате получим все возможные комбинации из 5 элементов по 3,которые различаются либо самими элементами, либо порядком элементов, т. е. все размещения из 5 элементов по 3. Всего мы получимразмещений.
каждом сочетании выполним все перестановки. Число перестановок из 3 элементов равно Р3. В результате получим все возможные комбинации из 5 элементов по 3,которые различаются либо самими элементами, либо порядком элементов, т. е. все размещения из 5 элементов по 3. Всего мы получимразмещений.
Зн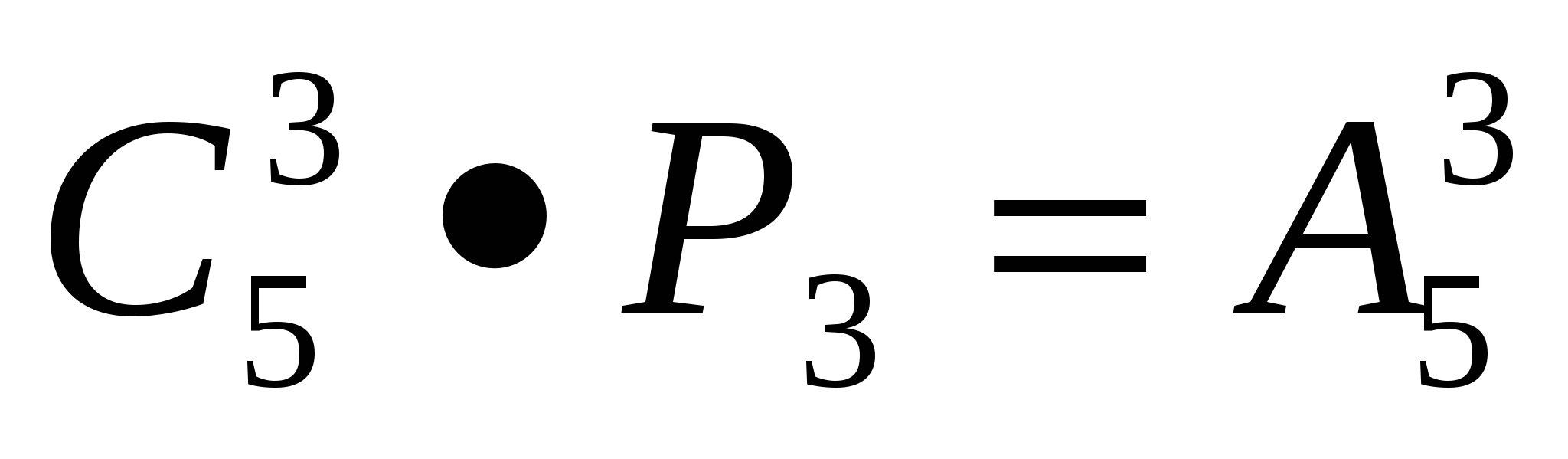 ачит,
ачит,
От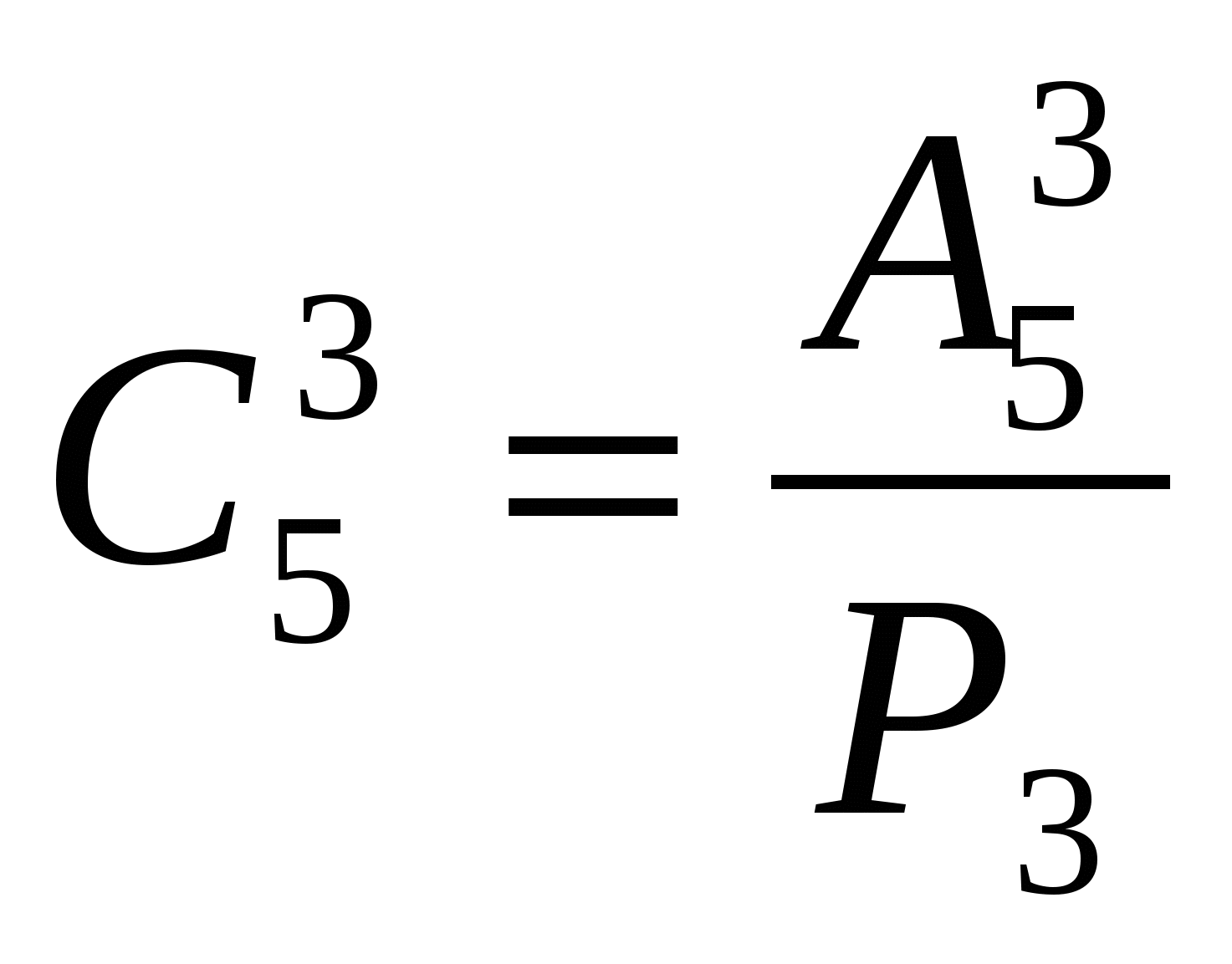 сюда
сюда
Ан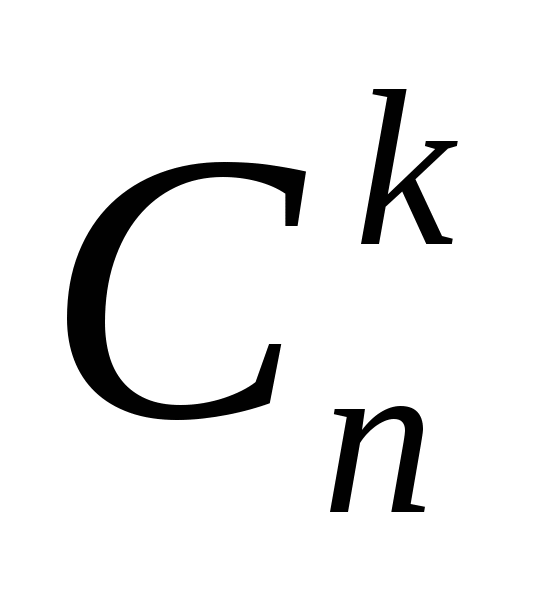 алогично будем рассуждать в общем случае. Допустим, что имеется множество, содержащие n элементов, и из его элементов составлены все возможные сочетания по k элементов. Число таких сочетаний равно .
алогично будем рассуждать в общем случае. Допустим, что имеется множество, содержащие n элементов, и из его элементов составлены все возможные сочетания по k элементов. Число таких сочетаний равно .
В 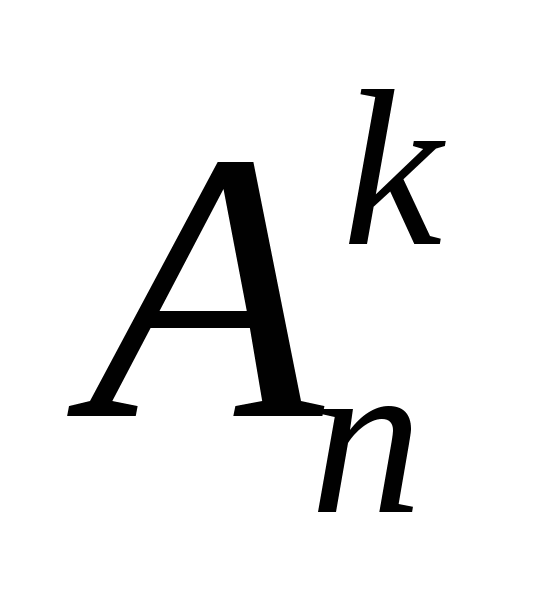 каждом сочетании можно выполнить Рk перестановок. В результате мы получим все размещения, которые можно составить из n элементов по k. Их число равно .
каждом сочетании можно выполнить Рk перестановок. В результате мы получим все размещения, которые можно составить из n элементов по k. Их число равно .
Зн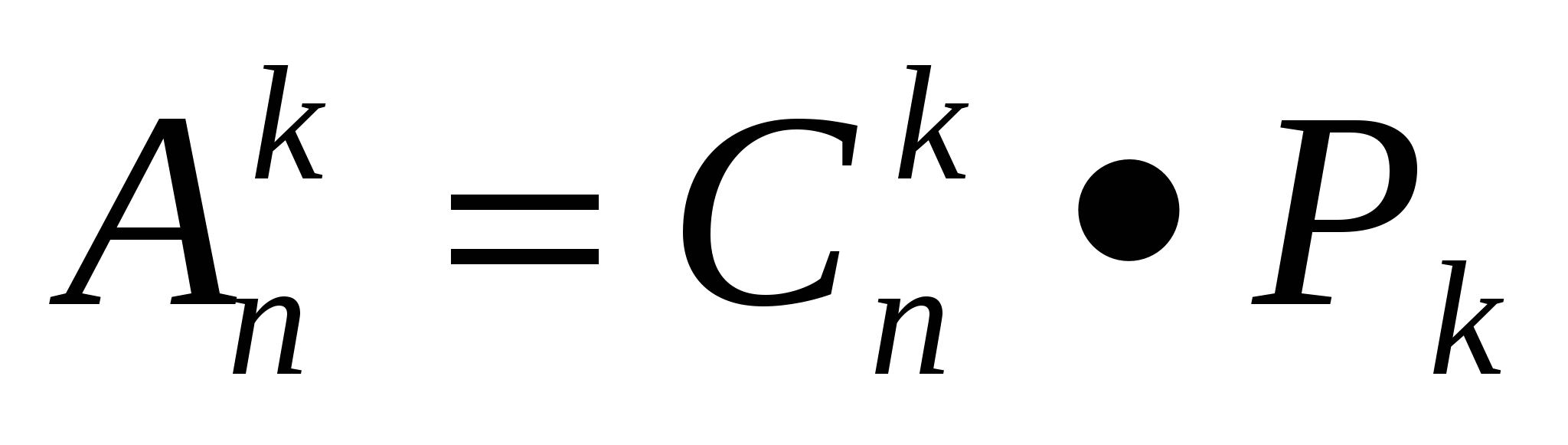 ачит,
ачит,
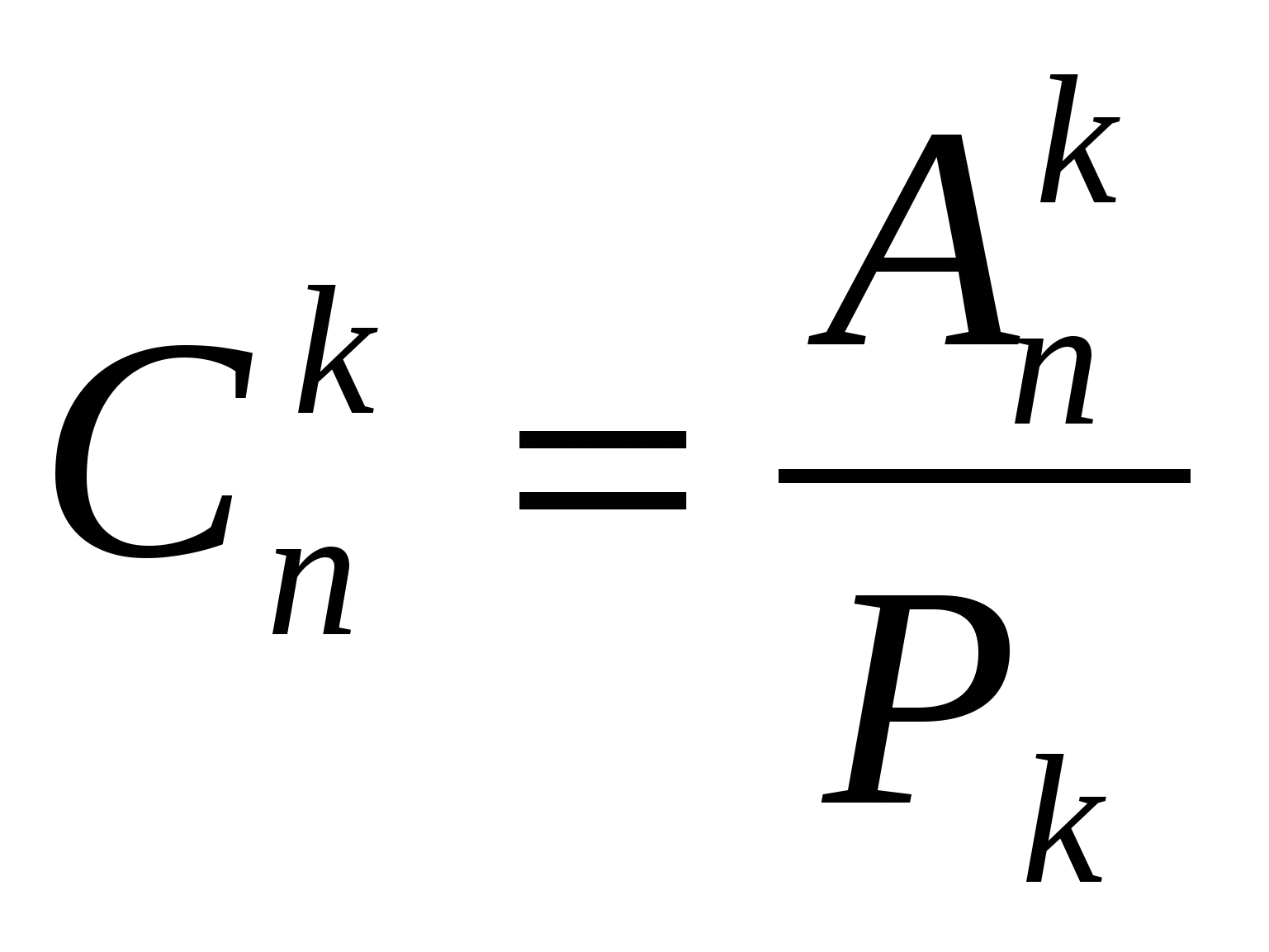
Отсюда
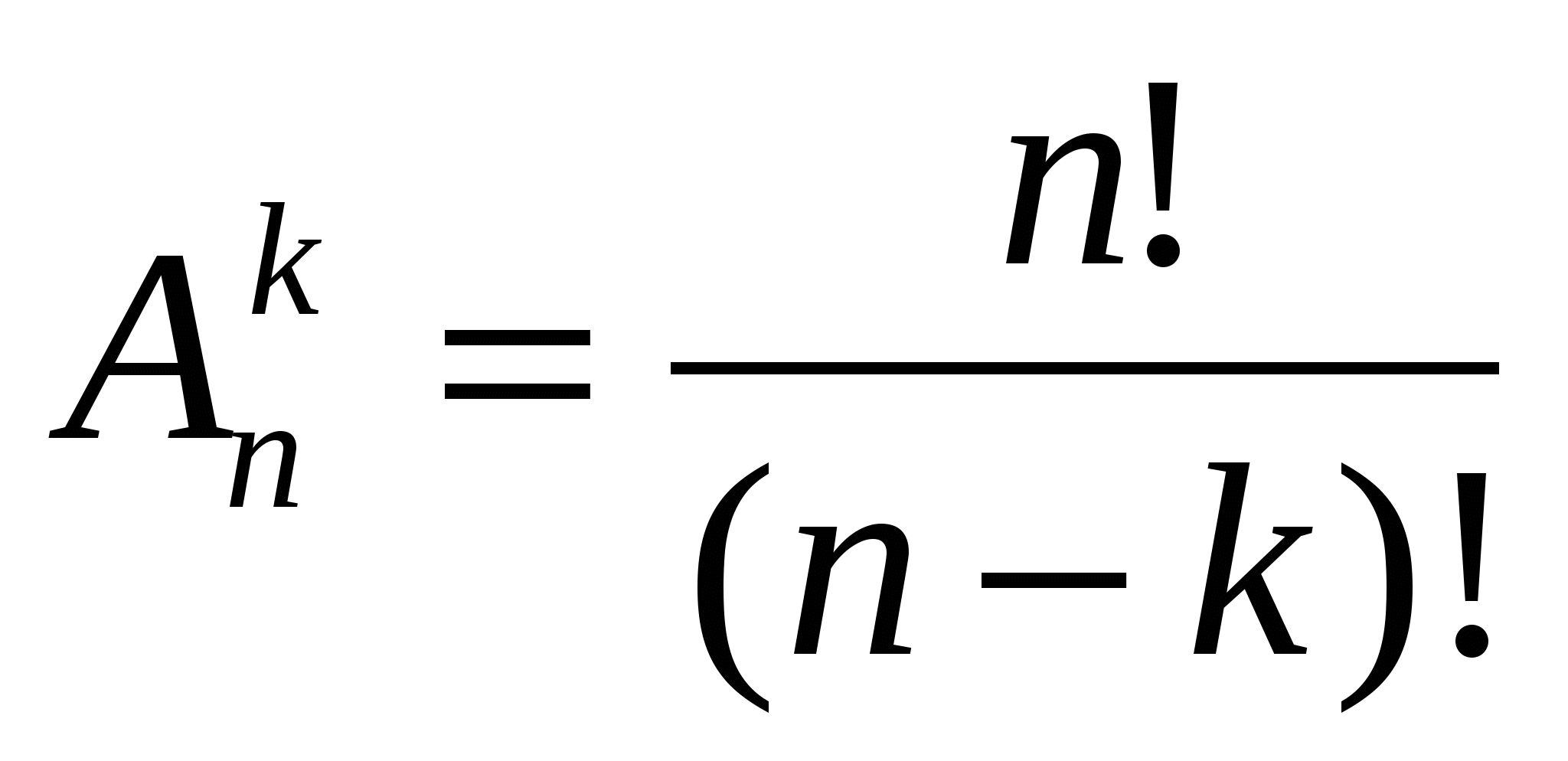
Пользуясь тем, что , где k≤n , находим, что
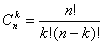
Мы получили формулу для вычисления числа сочетаний из n элементов по k при любом k≤n .
Приведем примеры.
Задача 1. В классе 30 учеников. Нужно избрать 5 человек на городской слет активистов. Сколькими способами это сделать?
Решение:
Та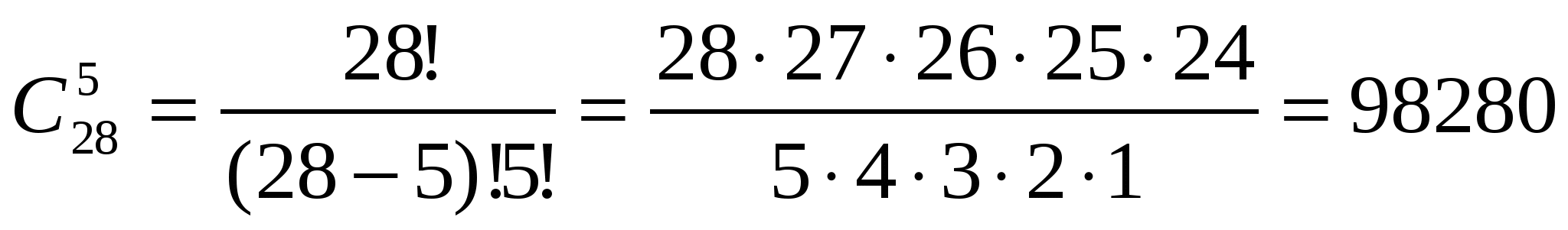 к как все делегаты обладают равными правами и обязанностями, то порядок в выборке не важен. Эти множества из 5 элементов будут отличаться друг от друга только составом. Значит, мы имеем дело с сочетаниями.
к как все делегаты обладают равными правами и обязанностями, то порядок в выборке не важен. Эти множества из 5 элементов будут отличаться друг от друга только составом. Значит, мы имеем дело с сочетаниями.
Ответ: 98280 способов.
Задача 2. Сколько различных стартовых шестерок можно образовать из числа 10 волейболистов?
Решение:
Та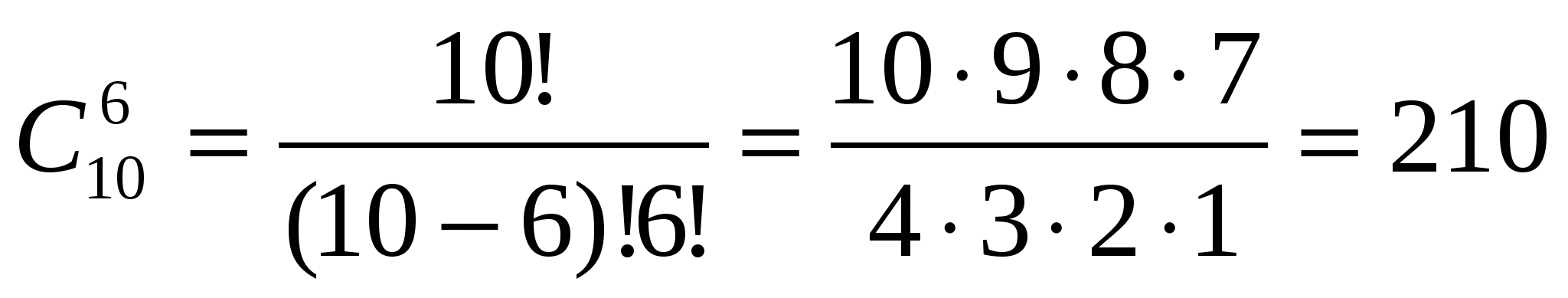 к как при игре в волейбол функции игроков практически равны, то значение имеет только состав шестерки. Тогда
к как при игре в волейбол функции игроков практически равны, то значение имеет только состав шестерки. Тогда
Ответ: 210 стартовых шестерок.
Задача 3.
В классе учатся 12 мальчиков и 10 девочек. Для уборки территории около школы требуется выделить 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
Решение:
Вы

 брать 3 мальчиков из 12 можно способами, а 2 девочек из 10 можно выбрать способами. Так как при каждом выборе мальчиков можно способами выбирать девочек, то сделать выбор учащихся, о котором говориться в задаче, можно ∙ способами.
брать 3 мальчиков из 12 можно способами, а 2 девочек из 10 можно выбрать способами. Так как при каждом выборе мальчиков можно способами выбирать девочек, то сделать выбор учащихся, о котором говориться в задаче, можно ∙ способами.
Им
 еем
еем
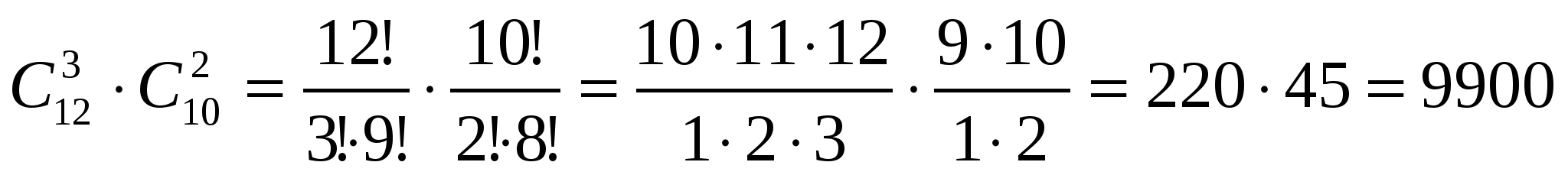
Значит, выбор учащихся для уборки территории можно сделать 9900 способами.
Гимнастика для глаз.
Обобщение знаний.
На каждую парту раздаются карточки со схемой.









Первичное осмысление и закрепление
В магазине «Филателия» продается 8 различных наборов марок, посвященных спортивной тематике. Сколькими способами можно выбирать из 3 набора?
Решение:
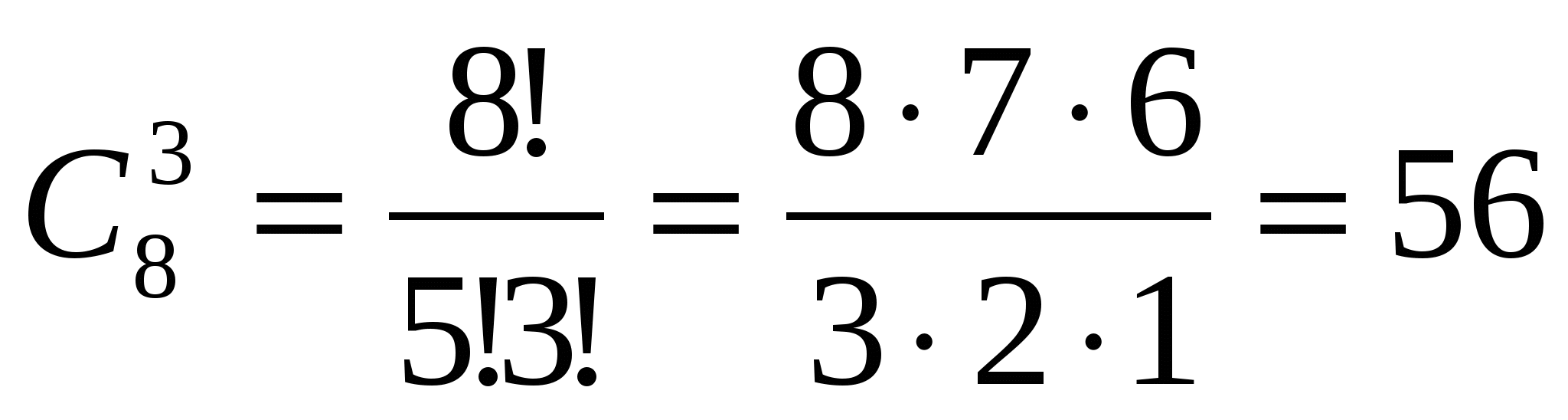
Ответ: 56 способами.
Из лаборатории, в которой работают заведующий и 10 сотрудников, надо отправить 5 человек в командировку. Сколькими способами это можно сделать, если: а) заведующий лабораторией должен ехать в командировку; б) заведующий лабораторией должен остаться?
Решение:
А) Если заведующий обязательно должен поехать в командировку, то нужно выбрать еще 4 человека из 10 сотрудников.
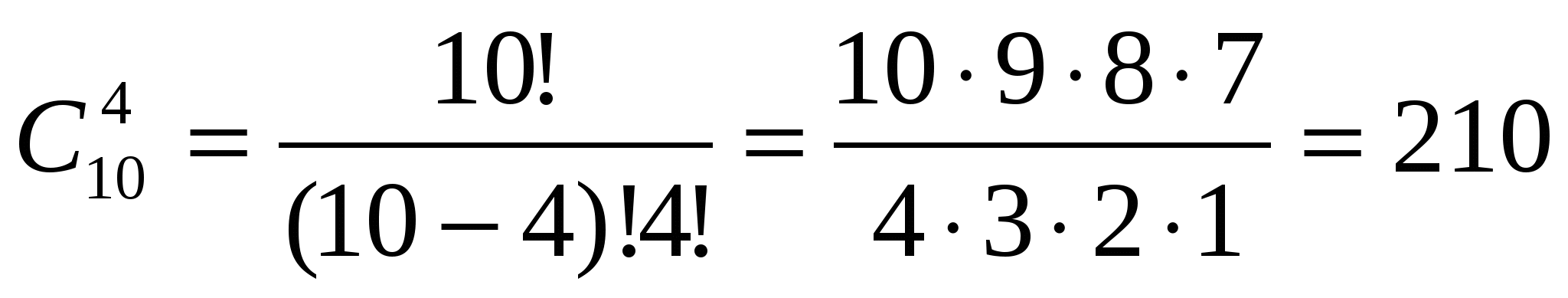
Ответ: 210 способов.
Б) если заведующий должен остаться, то надо выбирать 5 из 10.
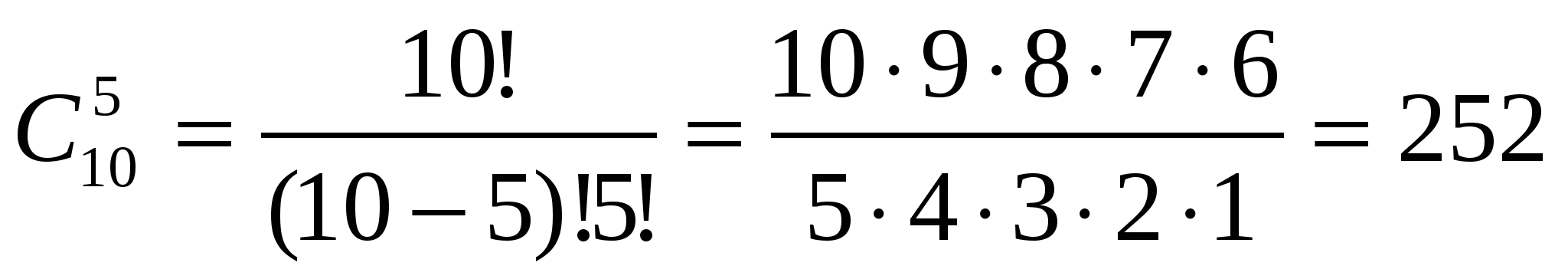
Ответ: 252 способа.
В классе учатся 16 мальчиков и 12 девочек. Для уборки территории требуется выделить 4 мальчиков и 3 девочек.
Сколькими способами это можно сделать?
Ре



 шение: Выбрать 4 мальчика из 16 можно способами, а выбрать 3 девочки из 12 можно способами. Так как при каждом выборе мальчиков, девочек можно выбирать способами, то сделать выбор, о котором говориться в задаче можно ∙ способами.
шение: Выбрать 4 мальчика из 16 можно способами, а выбрать 3 девочки из 12 можно способами. Так как при каждом выборе мальчиков, девочек можно выбирать способами, то сделать выбор, о котором говориться в задаче можно ∙ способами.
Им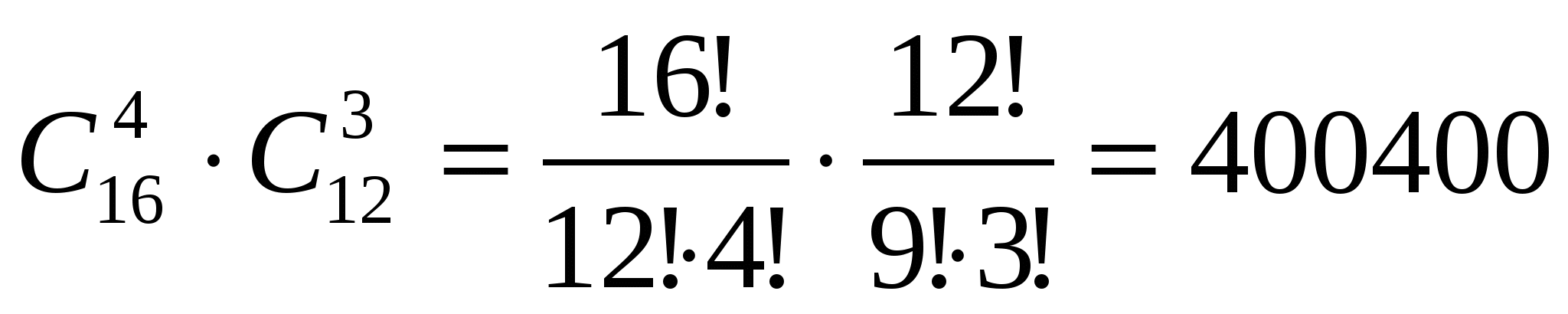 еем:
еем:
Ответ: 400400 способами.
Самостоятельная работа.
1 вариант
1. Из шести врачей поликлиники двух необходимо отправить на курсы повышения квалификации. Сколькими способами это можно сделать?
2. Сколько различных двухзначных чисел можно составить, используя цифры 1, 2, 3, 4 при условии, что ни одна цифра не повторяется?
2 вариант
1. В школьном хоре имеется пять солистов. Сколько есть вариантов выбора двух из них для участия в конкурсе?
2. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?
Подведение итогов урока, выставление оценок.
























