Число:
Тема урока: Радианная мера угла
Тип урока: урок ознакомления с новым материалом
Цель урока: познакомить учащихся с понятием радианная мера угла
Учебно-воспитательные задачи урока:
Образовательные
Рассмотреть связь между радианной и градусной мерами угла;
Закрепить умения выполнять переход от радианной меры угла к градусной мере и наоборот.
Развивающие
Развитие умений выделять главное, существенное в изученном материале
Формирований умений пользоваться алгоритмом перевода радианной меры угла к градусной мере и наоборот
Воспитательные
воспитания интереса к предмету
воспитание ответственного отношения к своему образованию.
Средства обучения: индивидуальные конспекты, записи на доске, учебник «Алгебра и начала математического анализа» 10-11 Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева, Н.Е.Федорова, М.И.Шабунин. М.: Просвещение, 2014.
План урока
| № | Этапы урока | время | Методы и методические приемы |
| 1 | Орг.момент | 1 мин | Словесный(приветствие) |
| 2 | Сообщение темы и целей урока | 1 мин | Словесный, практический |
| 3 | Изложение нового материала | 15 мин | Словесный, практический |
| 4 | Закрепление материала | 20 мин | Практический |
| 5 | Подведение итогов. Домашнее задание. Рефлексия | 3 мин | Словесный (запись на доске), оценивание |
8. Ход урока
I. Организационный момент. Приветствие учителя. Проверка готовности класса к уроку.
II. Сообщение темы и целей урока.
III. Объяснение нового материала.
Прежде, чем приступить к рассмотрению новой темы, давайте вспомним некоторые понятия из курса геометрии.
Окружность – это замкнутая линия, все точки которой равноудалены от центра.
Радиус окружности – отрезок, соединяющий её центр с любой лежащей на окружности точкой.
Круг – часть плоскости, ограниченная окружностью.
Дуга окружности – кривая линия, лежащая на окружности и ограниченная двумя точками.
Круговой сектор – часть круга, ограниченная двумя радиусами.
Градусом называют величину центрального угла, которому соответствует 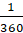 часть окружности.
часть окружности.
Градусная мера угла – это положительное число, которое показывает, сколько раз градус и его части укладываются в измеряемом угле.
Углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.
Давайте изобразим окружность с центром в точке 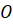 и радиусом
и радиусом 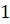 . Затем проведём вертикальную прямую, которая касается окружности в точке
. Затем проведём вертикальную прямую, которая касается окружности в точке 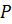 . Эту прямую мы будем считать числовой осью с началом отсчёта в точке
. Эту прямую мы будем считать числовой осью с началом отсчёта в точке 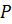 . Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
. Положительным направлением на прямой будем считать направление вверх. За единичный отрезок на числовой оси возьмём радиус окружности.
Отметим на прямой несколько точек: 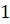 и
и 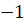 ,
,  и
и 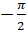 ,
, 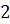 и
и  ,
,  и
и 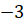 ,
, 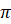 и
и 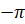 .
.
Т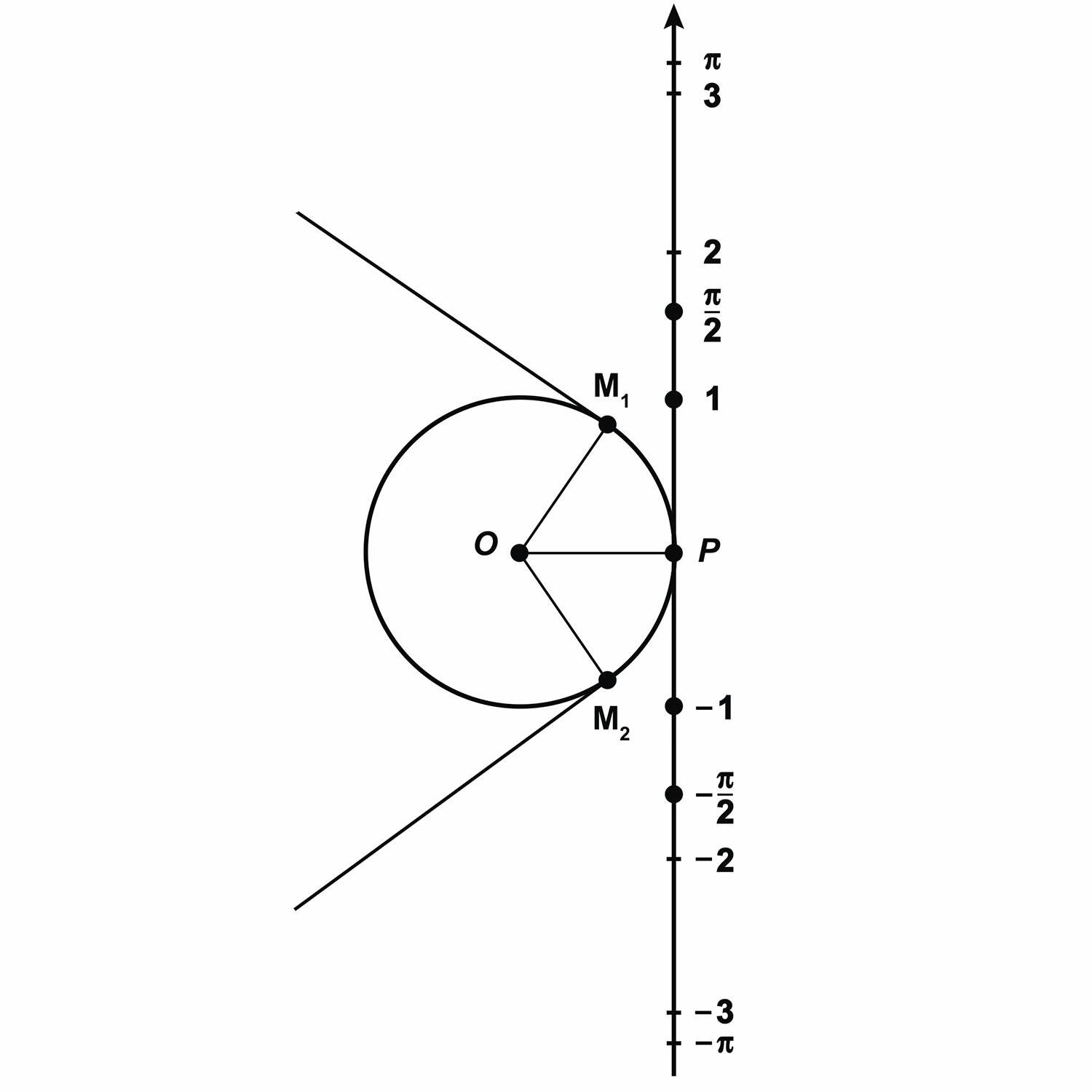 еперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке
еперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке 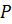 . Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами
. Будем наматывать нить на окружность. При этом точки на числовой прямой с координатами 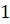 ,
, 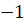 ,
,  ,
, 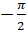 перейдут соответственно в точки окружности
перейдут соответственно в точки окружности 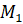 ,
, 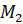 ,
, 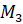 ,
, 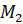 . При этом длина дуги
. При этом длина дуги  равна
равна 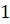 , длина дуги
, длина дуги  равна
равна 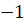 , длина дуги
, длина дуги  равна
равна  , длина дуги
, длина дуги  равна
равна 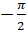 .
.
Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Т ак, точке прямой с координатой 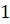 ставится в соответствие точка
ставится в соответствие точка 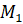 . А значит, угол
. А значит, угол  можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол
можем считать единичным? Да, и его мерой мы будем измерять другие углы. Например, угол  следует считать равным
следует считать равным  , а угол
, а угол  равным
равным 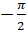 . Такой способ измерения углов считается измерением в радианной мере.
. Такой способ измерения углов считается измерением в радианной мере.
Единичный угол  называют углом в один радиан. Записывают так:
называют углом в один радиан. Записывают так: 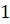 рад.
рад.
И напомним, что длина дуги  равна радиусу нашей окружности.
равна радиусу нашей окружности.
С ейчас давайте рассмотрим окружность радиуса  . И отметим на ней дугу
. И отметим на ней дугу  , равную длине радиуса окружности, и угол
, равную длине радиуса окружности, и угол  .
.
Определение. Углом в 1 радиан называется центральный угол, опирающийся на дугу, равную по длине радиусу окружности.
Обозначается 1рад.
Давайте найдём градусную меру угла в один радиан. Мы знаем из курса геометрии, что дуге длиной  , то есть полуокружности, соответствует центральный угол, равный
, то есть полуокружности, соответствует центральный угол, равный  . Следовательно, дуге окружности длиной
. Следовательно, дуге окружности длиной  соответствует угол в
соответствует угол в 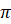 раз меньший.
раз меньший.
Выше мы назвали такой угол углом в один радиан, а значит, можем записать, что  рад
рад  .
.  , тогда
, тогда  рад .
рад .
Если угол содержит  рад, то
рад, то
 рад
рад  (1) -формула перехода от радианной меры к градусной.
(1) -формула перехода от радианной меры к градусной.
Пример: найдём градусную меру угла, равного  рад.
рад.
Воспользуемся формулой перехода от радианной меры к градусной. Подставим  вместо
вместо  : . Получим
: . Получим  .
.
Можно перейти от градусной меры к радианной: так как угол в  равен
равен  рад, то
рад, то  рад. Тогда
рад. Тогда
 рад (2) - формула перехода от градусной меры к радианной.
рад (2) - формула перехода от градусной меры к радианной.
Пример: найдём радианную меру угла, равного  .
.
Воспользуемся формулой перехода от градусной меры к радианной. Подставим  вместо
вместо  : . Получим
: . Получим  .
.
При обозначении меры угла в радианах слово «радиан» обычно не пишут:  .
.
Обозначение градуса в записи меры угла пропускать нельзя.
В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.
Радианная мера угла удобна для вычисления длины дуги окружности. Так, выше мы выяснили, что угол в 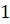 рад стягивает дугу, длина которой равна радиусу
рад стягивает дугу, длина которой равна радиусу  , а значит, угол в
, а значит, угол в  рад стягивает дугу длиной:
рад стягивает дугу длиной:  (3).
(3).
Если  , то эта формула принимает совсем простой вид:
, то эта формула принимает совсем простой вид:  , то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
, то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
Сейчас, прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового сектора радиуса  , образованного углом в
, образованного углом в  рад, равна
рад, равна  (4) , где
(4) , где  .
.
Докажем это. Известно, что площадь круга вычисляется по формуле:  Площадь полукруга, то есть кругового сектора в
Площадь полукруга, то есть кругового сектора в 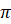 рад:
рад:  . Тогда площадь сектора в
. Тогда площадь сектора в 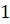 рад в
рад в 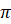 раз меньше, то есть
раз меньше, то есть  . Следовательно, площадь сектора в
. Следовательно, площадь сектора в  рад равна
рад равна  .
.
И немного истории: Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.
В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).
IV. Закрепление материала
Пример 1. Найти градусную меру угла, равного  рад.
рад.
Решение: Используя формулу (1),
находим  . Ответ:
. Ответ:  .
.
Пример 2. Найти радианную меру угла, равного 60 .
.
Решение:  рад
рад
 рад Ответ:
рад Ответ:  рад,
рад,  рад.
рад.
Пример 3. Найти длину дуги окружности радиуса 6 см, если её радианная мера  .
.
Решение: Используя формулу (3), получим: 
Ответ:  .
.
Пример 4. Найти площадь сектора, если радиус окружности 10 м, а радианная мера центрального угла  .
.
Решение: По формуле (4) вычисляем
Ответ: 45  м2
м2
Физкультминутка.
Дополнительные задания:
1. Найдите градусную меру угла, выраженную в радианах:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.
Решение.
2. Найдите радианную меру угла, выраженного в градусах:
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  .
.
Решение.
3. Чему равен радиус окружности, если дуге длиной  см соответствует центральный угол в
см соответствует центральный угол в  рад?
рад?
Решение.
4. Дуге кругового сектора соответствует угол, равный  рад. Чему равна площадь сектора, если радиус круга равен
рад. Чему равна площадь сектора, если радиус круга равен 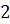 см?
см?
Решение.
V. Итоги урока. Рефлексия
Домашнее задание. П.21 . №№ 407,408, 411.







 еперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке
еперь представим нашу прямую в виде нерастяжимой нити, которая закреплена на окружности в точке 









