МИНИСТЕРСТВО ОБРАЗОВАНИЯ СТАВРОПОЛЬСКОГО КРАЯ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
"НЕФТЕКУМСКИЙ РЕГИОНАЛЬНЫЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ"
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
для проведения практических работ
для специальности
21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений
ЕН.01 МАТЕМАТИКА
| ОДОБРЕНО: на заседании МО Протокол №_1_ «30» августа 2023 г. Руководитель МО педагогов естественнонаучных и математических дисциплин
_________________/ С.А.Федорченко /
| Методические указания составлены в соответствии с требованиями Федерального государственного образовательного стандарта среднего профессионального образования по специальности 21.02.01 Разработка и эксплуатация нефтяных и газовых месторождений
|
| УТВЕРЖДАЮ:
Заместитель директора по учебно-методической работе ____________________/С.Г.Усенко / |
Составитель Федорченко Александр Сергеевич, преподаватель ГБПОУ НРПК
Рецензент: Федорченко Светлана Анатольевна, преподаватель ГБПОУ НРПК
Оглавление
Практическая работа 1. Выполнение операций над матрицами. Вычисление определителей 4
Практическая работа 2. Решение систем линейных уравнений различными методами 9
Практическое занятие 3. Выполнение действий над комплексными числами в алгебраической форме 16
Практическая работа 4. Выполнение действий над комплексными числами в тригонометрической и показательной формах 19
Практическая работа 5. Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей 23
Практическая работа 6. Вычисление односторонних пределов, классификация точек разрыва 29
Практическая работа 7. Вычисление производных сложных функций 33
Практическая работа 8. Дифференциал функции. Приближенные вычисления 38
Практическая работа 9. Применение производной для исследования функции и построения графика 40
Практическая работа 10. Вычисление неопределенного интеграла 42
Практическая работа 11. Приложение определённого интеграла к решению прикладных задач 44
Практическая работа 12. Решение дифференциальных уравнений первого порядка 47
Практическая работа 13. Определение сходимости рядов 49
Практическая работа 14. Решение простейших вероятностных задач. Вычисление числовых характеристик случайной величины 52
Практическая работа 1. Выполнение операций над матрицами. Вычисление определителей
Образец выполнения, методические рекомендации:
Задание 1.
Пусть 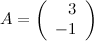 .
.
Найти матрицу  .
.
Решение. 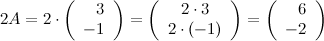
Ответ.
Задание 2.Найти  , если
, если
 ,
, 
Решение.

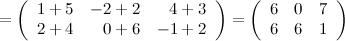
Ответ
. 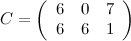
Задание 3. Найти матрицу 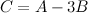 ,
,
если 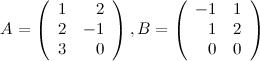
Решение. 
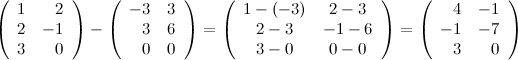
Ответ.

Задание 4. Вычислить  и
и 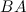 ,
,
если

Решение. Так как 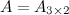 , а
, а 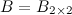 , то произведение возможно и результатом операции умножения будет матрица
, то произведение возможно и результатом операции умножения будет матрица 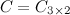 , а это матрица вида
, а это матрица вида 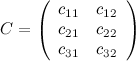 .
.
Вычислим элементы матрицы  :
:






Итак,  .
.
Выполним произведения в более компактном виде:
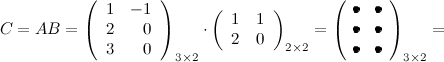

Найдем теперь произведение 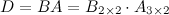 . Так как количество столбцов матрицы
. Так как количество столбцов матрицы  (первый сомножитель) не совпадает с количеством строк матрицы
(первый сомножитель) не совпадает с количеством строк матрицы  (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
(второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. 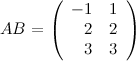 . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
. В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы  не совпадает с количеством строк матрицы
не совпадает с количеством строк матрицы  .
.
Задание 5. Найти матрицу 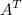 , если
, если
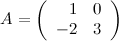
Решение.

Ответ.

Задание 6. Найти минор  к элементу
к элементу  определителя
определителя
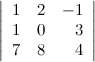 .
.
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:

тогда
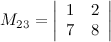
Ответ.
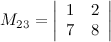
Задание 7. Найти алгебраическое дополнение  к элементу
к элементу  определителя
определителя
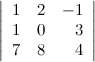 .
.
Решение.
 = - (1.8-7.2)= - (8-14)=6
= - (1.8-7.2)= - (8-14)=6
Ответ. 6
Задание 8. Вычислить определитель матрицы.
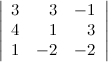
Решение.
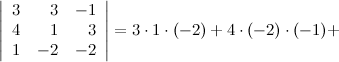
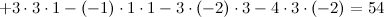
Ответ. 54
Задание 9. Найти обратную матрицу к матрице
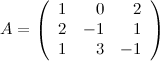
Решение. Вычисляем определитель матрицы:
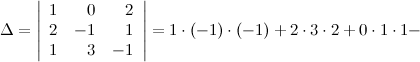
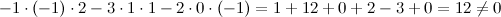
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица 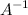 к матрице
к матрице  находится по формуле:
находится по формуле:

Найдем союзную матрицу 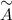 , для этого вычислим алгебраические дополнения к элементам матрицы
, для этого вычислим алгебраические дополнения к элементам матрицы  :
:
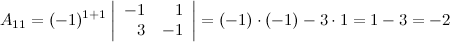


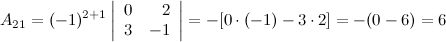


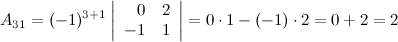


Таким образом, 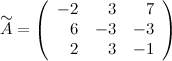
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):

Итак,

Ответ.

Задания:
Найти матрицу 2А.
Найти А+В.
Найти С = А-3В.
Вычислить А·В и В·А
Найти транспонированную матрицу
Найти минор М23 к элементу а23 определителя
Найти алгебраическое дополнение А23 к элементу а23 определителя.
Вычислить определитель матрицы
Найти обратную матрицу
Возвести матрицу в квадрат.
| Вариант1. | 
|  2 8 5 2 8 5 |  | - 1 -2 3 1 -2 3 | | | А= | -4 1 3 | В= | 1 -2 1 | | | | 8 -2 -6 | | 1 3 4 | |
| Вариант 11. |  | 2 -1 0 -1 0 |  | - 2 0 3 2 0 3 | | | А= | -2 2 0 | В= | 4 1 2 | | | | 1 -1 1 | | -2 1 0 | |
|
| Вариант 2. |  | 1 4 3 4 3 |  | - 2 1 1 2 1 1 | | | А= | -8 2 -5 | В= | -2 -1 3 | | | | 1 1 -1 | | 3 1 -4 | |
| Вариант 12. | 
|  5 -1 -1 5 -1 -1 |  |  1 4 1 1 4 1 | | | А= | 0 4 -1 | В= | 0 3 1 | | | | 0 -1 4 | | 2 1 0 | |
|
| Вариант 3. | . | - 6 8 -2 6 8 -2 |  | - 4 3 1 4 3 1 | | А= | 5 2 8 | В= | 1 -2 1 | | | 3 -4 1 | | 3 -2 -1 |
| Вариант 13. | 
|  2 1 0 2 1 0 |  |  0 -1 1 0 -1 1 | | | А= | 1 2 0 | В= | 3 1 2 | | | | -1 1 3 | | 2 1 0 | |
|
| Вариант 4. | 
|  2 -8 -5 2 -8 -5 |  | - 1 3 -2 1 3 -2 | | | А= | 4 1 3 | В= | 1 -4 3 | | | | -8 -2 -6 | | 1 1 -2 | |
| Вариант 14.
| 
|  7 2 -2 7 2 -2 |  |  1 2 -1 1 2 -1 | | | А= | 4 5 -2 | В= | 0 1 3 | | | | 0 0 3 | | 2 0 -5 | |
|
| Вариант 5. | 
|  1 4 -3 1 4 -3 |  | - 3 -2 1 3 -2 1 | | | А= | -8 2 5 | В= | -2 -3 -1 | | | | 2 8 -6 | | 4 3 -1 | |
| В  ариант 15. ариант 15. |  |  3 0 0 3 0 0 | | 0 3 1 | | | А= | 1 2 -1 | В= | 1 -2 4 | | | | 1 -1 2 | | 2 1 1 | |
|
| В ариант 6. ариант 6. |
|  2 -8 5 2 -8 5 |  | - 1 3 4 1 3 4 | | | А= | 4 1 -3 | В= | -1 -3 -2 | | | | 8 2 -6 | | 1 -2 -3 | |
| В   ариант 16. ариант 16. |
|  3 -1 -1 3 -1 -1 | | 0 2 1 | | | А= | 0 2 -1 | В= | -3 1 0 | | | | 0 -1 2 | | 1 2 3 | |
|
| В ариант 7. ариант 7. | 
| - 6 -2 8 6 -2 8 |  | -3 -2 -1 | | | А= | 3 1 -4 | В= | -2 -3 1 | | | | 5 8 2 | | 3 4 -1 | |
| Вариант 17. |  |  2 0 -1 2 0 -1 |  | - 2 1 -3 2 1 -3 | | | А= | 1 1 -1 | В= | 0 3 0 | | | | -1 0 2 | | 1 2 -1 | |
|
| Вариант 8. |
| 1  -4 3 -4 3 |  | - 3 1 -2 3 1 -2 | | | А= | 8 2 5 | В= | 4 -1 3 | | | | -2 8 -6 | | -2 -1 -3 | |
| Вариант 18. | 
| 4 1 0 1 0 |  |  0 2 3 0 2 3 | | | А= | 1 4 0 | В= | 1 1 3 | | | | -1 1 5 | | 2 4 2 | |
|
| Вариант 9. |
| -  6 -8 2 6 -8 2 |  | - 4 1 3 4 1 3 | | | А= | -5 2 8 | В= | 3 -1 -2 | | | | -3 -4 1 | | 1 1 -2 | |
| В ариант 19. ариант 19. | 
| 9 0 0 |  | - 2 1 0 2 1 0 | | | А= | 2 7 -4 | В= | -1 2 3 | | | | 2 -2 5 | | 2 1 1 | |
|
| Вариант 10. | 
| 2 -5 -8 -5 -8 |  | - 1 4 3 1 4 3 | | | А= | -8 -6 -2 | В= | 1 -3 -2 | | | | 4 3 1 | | -1 -2 -3 | |
| Вариант 20. | 
| 5 0 0 0 0 |  |  0 1 2 0 1 2 | | | А= | 1 4 -1 | В= | 2 1 3 | | | | 1 -1 4 | | 0 3 1 | |
|
Практическая работа 2. Решение систем линейных уравнений различными методами
Методические рекомендации
1. Система линейных уравнений
О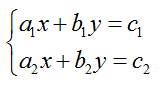 бычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
бычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
(1)
Система уравнений такого вида, где a, b, c – числа, а x, y - переменные, называется системой линейных уравнений.
При решении системы уравнений используют свойства, справедливые для решения уравнений.
2. Решение системы линейных уравнений способом подстановки
Рассмотрим пример 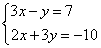
1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:
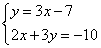
2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:
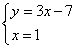
4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x = 1, y = - 4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй - y.
3. Решение системы линейных уравнений способом сложения
Решим систему уравнений из предыдущего примера 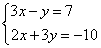 методом сложения.
методом сложения.
1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на "3".
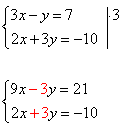
2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.
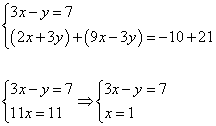
3) Полученное решение подставляем в первое уравнение системы:
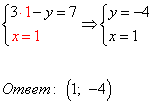
4. Решение системы линейных уравнений графическим способом
Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.
Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.
2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.
Графическое решение системы 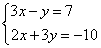
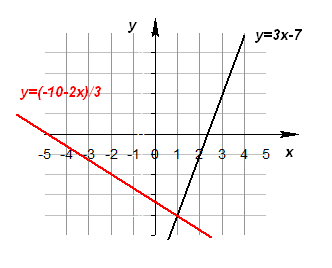 Ответ: (1; -4).
Ответ: (1; -4).
5. Особые случаи
Н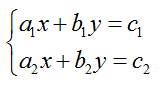 е решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
е решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.
Пусть дана система (1)
1 ) Если , то система (1) имеет единственное решение.
) Если , то система (1) имеет единственное решение.

2) Если ,, то система (1) решений не имеет.
В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.
 .
.
3 ) Если , то система (1) имеет бесконечное множество решений.
) Если , то система (1) имеет бесконечное множество решений.
В этом случае прямые совпадают друг с другом.
 .
.
6. Решение систем линейных уравнений по формулам Крамера
Историческая справка
Габриель Крамер (1704–1752) швейцарский математик.
Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, то есть ни одно уравнение не являлось бы линейной комбинацией остальных. Для этого необходимо, чтобы определитель системы не равнялся  .
.
Действительно, если какое-либо уравнение системы есть линейная комбинация остальных, то если к элементам какой-либо строки прибавить элементы другой, умноженные на какое-либо число, с помощью линейных преобразований можно получить нулевую строку. Определитель в этом случае будет равен нулю.
Система из двух уравнений с двумя неизвестными
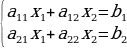
решается с помощью формул Крамера:
 ,
, 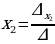 ,
,
где  и
и 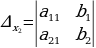 ,
,  .
.
При решении системы возможны три случая:
1. Определитель системы  . Тогда система имеет единственное решение, определяемое формулами Крамера.
. Тогда система имеет единственное решение, определяемое формулами Крамера.
2. Определитель системы  . Если при этом хотя бы один из определителей
. Если при этом хотя бы один из определителей 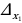 и
и 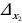 не равен нулю, то система не имеет решений.
не равен нулю, то система не имеет решений.
3. Если  ,
,  и
и  , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
, то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
П р и м е р 1. Решить систему уравнений  .
.
Решение. Вычислим определитель системы  , и дополнительные определители
, и дополнительные определители 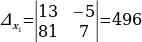 ,
, 
Система имеет единственное решение
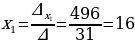 ,
, 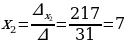
Ответ: 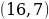 .
.
П р и м е р 2. Решить систему уравнений 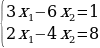 .
.
Решение. Вычислим определитель системы 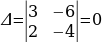 , и дополнительные определители
, и дополнительные определители  ,
,  . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
. Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
Ответ: нет решений.
П р и м е р 3. Решить систему уравнений 
Решение. Вычислим определитель системы 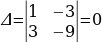 , и дополнительные определители
, и дополнительные определители 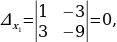
 .
.
Так как 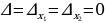 , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на
, то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на  ).
).
Система сводится к одному уравнению и имеет бесчисленное множество решений, каждое из которых вычисляется по формуле:  , где числовые значения
, где числовые значения 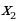 задаются произвольно и вычисляются соответствующие значения
задаются произвольно и вычисляются соответствующие значения  .
.
Ответ:  – общее решение данной системы, а решения
– общее решение данной системы, а решения 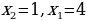 – частные.
– частные.
Система из трех уравнений с тремя неизвестными
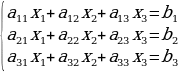
При решении системы из трех уравнений с тремя неизвестными возможны три случая:
1. Определитель системы  . Система имеет единственное решение, определяемое формулами Крамера
. Система имеет единственное решение, определяемое формулами Крамера 
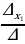 ,
,
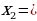
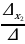 ,
,  , где
, где  и
и 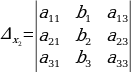 ,
, 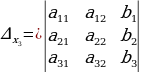 ,
,  .
.
2. Определитель системы равен нулю,  . Если при этом хотя бы один из определителей
. Если при этом хотя бы один из определителей  , не равен нулю, то система несовместна, решений не имеет.
, не равен нулю, то система несовместна, решений не имеет.
3. Если  и
и  , то система имеет бесчисленное множество решений.
, то система имеет бесчисленное множество решений.
П р и м е р 4. Решить систему уравнений 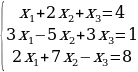
Решение. Вычислим определитель системы  и дополнительные определители
и дополнительные определители
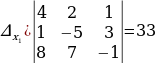
и  ,
, 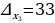 .
.
По формулам Крамера имеем, что 
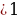 .
.
Ответ:  .
.
7. Метод Гаусса
Метод Гаусса, называемый также методом последовательного исключения неизвестных, состоит в том, что при помощи элементарных преобразований систему линейных уравнений приводят к такому виду, чтобы её матрица из коэффициентов оказалась трапециевидной или близкой к трапециевидной.
Решите систему линейных уравнений методом Гаусса.
Решение. Выпишем расширенную матрицу системы и при помощи элементарных преобразований над ее строками приведем эту матрицу к ступенчатому виду (прямой ход) и далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Вначале поменяем первую и вторую строку, чтобы элемент 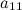 равнялся 1 (это мы делаем для упрощения вычислений):
равнялся 1 (это мы делаем для упрощения вычислений):


Далее делаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей - три первых: 
Все элементы третьей строки делим на два 
Далее делаем нули во втором столбце под главной диагональю, для удобства вычислений поменяем местами вторую и третью строки, чтобы диагональный элемент равнялся 1:
 От третьей строки отнимаем вторую, умноженную на 3:
От третьей строки отнимаем вторую, умноженную на 3:  Умножив третью строку на 0,5 , получаем:
Умножив третью строку на 0,5 , получаем: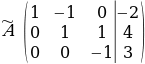
Проведем теперь обратный ход метода Гаусса (метод Гассу-Жордана), то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Надо обнулить элемент  , для этого от второй строки отнимем третью:
, для этого от второй строки отнимем третью: 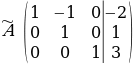
Далее обнуляем недиагональные элементы второго столбца, к первой строке прибавляем вторую: 
Полученной матрице соответствует система

 Ответ.
Ответ. 
Задания для самостоятельного решения:
Задания для самостоятельного решения:
Решить систему уравнений методом сложения:
| х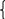 +у= -1 +у= -1 2х-у=4 | 3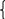 х+у= 1 х+у= 1 2х-у=4 | х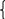 +5у= -9 +5у= -9 2х-5у=12 |
| х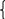 +2у= 3 +2у= 3 х-2у= -5 | 2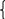 х+у= 0 х+у= 0 -2х+у= 4 | -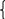 3х+у= 5 3х+у= 5 3х-3у= -9 |
Решить предыдущее задание методом подстановки.
Решить графически систему уравнений:
| 2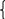 х+у= 0 х+у= 0 -2х+у= 4 | х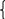 +у= -1 +у= -1 2х-у=4 | 3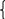 х+у= 1 х+у= 1 2х-у=4 |
Решить систему уравнений по формулам Крамера:
Решить систему линейных уравнений методом Гаусса:
Практическое занятие 3. Выполнение действий над комплексными числами в алгебраической форме
Теоретические сведения, методические рекомендации
Комплексное число — это выражение вида a + bi, где a, b — действительные числа, а i — так называемая мнимая единица, символ, квадрат которого равен –1, то есть i2 = –1.
Число a называется действительной частью, а число b — мнимой частью комплексного числа z = a + bi.
Если b = 0, то вместо a + 0i пишут просто a.
Действительные числа — это частный случай комплексных чисел.
Сложение и вычитание происходят по правилу
(a + bi) ± (c + di) = (a ± c) + (b ± d)i,
а умножение — по правилу (a + bi) · (c + di) = (ac – bd) + (ad + bc)i (здесь как раз используется, что i2 = –1).
Примеры. Найдите сумму, разность, произведение комплексных чисел
z1=2-3i
z2=-4+5i
z1+ z2=(2-3i)+(-4+5i)=(2+(-4))+(-3i+5i)=-2+2i
z1- z2=(2-3i)-( -4+5i)=(2-(-4))+(-3i-5i)=6-8i
z1 . z2=(2-3i)( -4+5i)=-8+10i+12i-15i2=-8+10i+12i+15=7+22i
Число 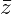 = a – bi называется комплексно-сопряженным к z = a + bi.
= a – bi называется комплексно-сопряженным к z = a + bi.
Примеры. Запишите комплексно сопряженное число
1) z=3-4i 2) z=-13+i
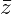 = 3+4i
= 3+4i 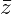 = -13-i
= -13-i
Равенство z · 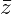 = a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
= a2 + b2 позволяет понять, как делить одно комплексное число на другое (ненулевое) комплексное число:
 .
.
Пример Найти частное
 =
= 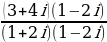 =
=  =
=  =
= =
= 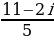 =
=  -
- 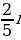
У комплексных чисел есть удобное и наглядное геометрическое представление: число z = a + bi можно изображать вектором с координатами (a; b) на декартовой плоскости (или, что почти то же самое, точкой — концом вектора с этими координатами):

Примеры: Изобразите комплексные числа на плоскости
а) z= -3+2i б) z = 4 в) z = -5i

 y y y
y y y


 2 0 x
2 0 x


 -3 0 x 0 4 x
-3 0 x 0 4 x
 -5
-5
По теореме Пифагора длина вектора с координатами (a; b) равна 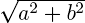 . Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|.
. Эта величина называется модулем комплексного числа z = a + bi и обозначается |z|.
|z|=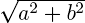
Пример: Найдите модуль комплексного числа
z=4-3i
|z|=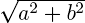 =
= 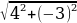 =
=
Задания для самостоятельного выполнения:
Вариант 1
Найдите сумму комплексных чисел 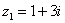 ,
, 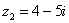 .
.
Найти разность комплексных чисел  , если
, если 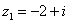 , z2= 3 + 5i.
, z2= 3 + 5i.
Найти произведение комплексных чисел  ,
,  .
.
Даны комплексные числа  ,
, 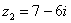 . Найти частное
. Найти частное 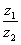 .
.
Найти частное комплексных чисел  .
.
Изобразите комплексные числа на плоскости: а) z=-2+3i; б) z=-7; в) z=3+3i; г) z=3i.
Запишите комплексно сопряженное число: z=-8+i
Найдите модуль комплексного числа: z=8-6i
Даны два комплексных числа  ,
, 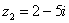 . Найти их сумму, разность, произведение и частное.
. Найти их сумму, разность, произведение и частное.
Вариант 2
Найдите сумму комплексных чисел z1=2 – 4i, z2=3+2i.
Найти разность комплексных чисел  , если z1=-3+2i, z2=1+i .
, если z1=-3+2i, z2=1+i .
Найти произведение комплексных чисел z1=1 – 2i, z2=3+i
Даны комплексные числа z1=2 – 4i, z2=3+2i. Найти частное 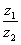 .
.
Найти частное комплексных чисел  .
.
Изобразите комплексные числа на плоскости: a) z=2+3i; б) z=7; в) z=1+2i; г) z=4i.
Запишите комплексно сопряженное число: z=6+2i
Найдите модуль комплексного числа: z=4-3i
Даны два комплексных числа z1=2 +5i, z2=3-4i . Найти их сумму, разность, произведение и частное.
Практическая работа 4. Выполнение действий над комплексными числами в тригонометрической и показательной формах
Теоретические сведения и методические рекомендации
Комплексным числом  называется число вида
называется число вида  , где
, где  и
и  – действительные числа,
– действительные числа, 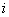 – так называемая мнимая единица (i2 = – 1). Число
– так называемая мнимая единица (i2 = – 1). Число  называется действительной частью (
называется действительной частью (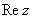 )комплексного числа
)комплексного числа  , число
, число  называется мнимой частью (
называется мнимой частью (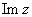 ) комплексного числа
) комплексного числа  .
.
 – это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:
– это ЕДИНОЕ ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами: 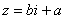 или переставить мнимую единицу:
или переставить мнимую единицу: 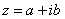 – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке:
– от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 
Комплексные числа обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат. Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому что они сливаются с осями.
А лгебраическая форма комплексного числа -
лгебраическая форма комплексного числа - 
Сложение комплексных чисел: для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части
(a + bi) + (c + di) = (a + c) + (b + d)i.
Пример 1: Сложить два комплексных числа 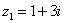 и
и 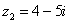 .
.
 .
.
Вычитание комплексных чисел: действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака
(a + bi) – (c + di) = (a – c) + (b – d)i.
Пример 2: Найти разности комплексных чисел 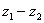 и
и 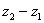 , если
, если 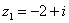 ,
,  .
.

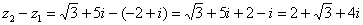
Умножение комплексных чисел: (a + bi)(c + di) = (aс + bd) + (ad + bc)i
Пример 3: Найти произведение комплексных чисел  ,
, 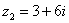
 .
.
Деление комплексных чисел: методом умножения знаменателя и числителя на сопряженное знаменателю выражение 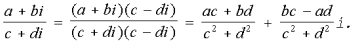
Пример 4: Даны комплексные числа  ,
,  . Найти частное
. Найти частное 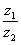 .
.

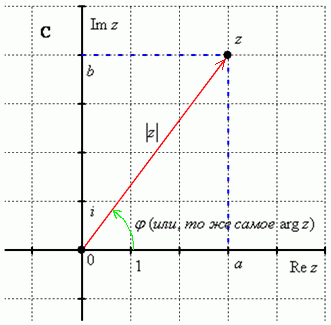
Любое комплексное число (кроме нуля)  можно записать в тригонометрической форме:
можно записать в тригонометрической форме: 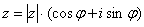 , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.
Модулем комплексного числа  называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора. Модуль комплексного числа
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора. Модуль комплексного числа  стандартно обозначают:
стандартно обозначают:  или
или 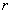 .
.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: 
Аргументом числа  называется угол
называется угол  между положительной полуосью действительной оси
между положительной полуосью действительной оси 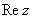 и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:  .
.
Аргумент комплексного числа  стандартно обозначают:
стандартно обозначают:  или
или 
Из геометрических соображений получается следующая формула для нахождения аргумента: 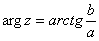 .
.
Пример 5: Представим в тригонометрической форме число  . Найдем его модуль и аргумент. Очевидно, что
. Найдем его модуль и аргумент. Очевидно, что 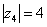 . Формальный расчет по формуле:
. Формальный расчет по формуле:  .
.
Аргумент:  (270 градусов), и, соответственно:
(270 градусов), и, соответственно:  . Проверка:
. Проверка:  .
.
Показательная форма комплексного числа: Любое комплексное число (кроме нуля)  можно записать в показательной форме:
можно записать в показательной форме:
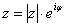 , где
, где  – это модуль комплексного числа, а
– это модуль комплексного числа, а  – аргумент комплексного числа.
– аргумент комплексного числа.
Задание:
1. Ответить на вопросы допуска:
1. Какие числа называют комплексными?
2. Запишите основное свойство мнимой единицы?
3. Что такое модуль комплексного числа?
2.Выполнить:
| Вариант 1. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 2-4i ; б) z = 4; в) z = -3i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1=3+7i и z2=1-2i. 3. Найдите модуль и аргумент комплексного числа z = -1+2i . 4. Запишите число z = 4+4i в тригонометрической и показательной формах.
| Вариант 2. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 6-i ; б) z = 4i; в) z = -6 . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1=3+2i и z2=1-2i. 3. Найдите модуль и аргумент комплексного числа z = 5-2i . 4. Запишите число z = 2-3i в тригонометрической и показательной формах. |
|
Вариант 3. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = -2-5i ; б) z = -5; в) z = -4i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1 = -6-4i и z2=1+2i. 3. Найдите модуль и аргумент комплексного числа z = -2+2i . 4. Запишите число z = 3-3i в тригонометрической и показательной формах.
|
Вариант 4. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 6-5i ; б) z = 4; в) z = 2i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1=6+5i и z2=1-3i. 3. Найдите модуль и аргумент комплексного числа z = -7-7i . 4. Запишите число z = 1- i в тригонометрической и показательной формах. i в тригонометрической и показательной формах. |
|
Вариант 5. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 8-5i ; б) z = -3; в) z = 6i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1=6+5i и z2=1-3i. 3. Найдите модуль и аргумент комплексного числа z = -7-7i . 4. Запишите число z =  - - i в тригонометрической и показательной формах. i в тригонометрической и показательной формах.
|
Вариант 6. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 5+4i ; б) z = -6; в) z = 5i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1=-9+5i и z2= -1-4i. 3. Найдите модуль и аргумент комплексного числа z =7-7i . 4. Запишите число z = 3- i в тригонометрической и показательной формах. i в тригонометрической и показательной формах. |
| Вариант 7. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = -6+2i ; б) z = 7; в) z = -i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1= -8+5i и z2=9-3i. 3. Найдите модуль и аргумент комплексного числа z = -6+6i . 4. Запишите число z =  -i в тригонометрической и показательной формах. -i в тригонометрической и показательной формах.
| Вариант 8. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = -4+7i ; б) z = -2; в) z = 3i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1= 11-9i и z2=9-11i. 3. Найдите модуль и аргумент комплексного числа z =  -i. -i. 4. Запишите число z = -6+6i в тригонометрической и показательной формах. |
|
Вариант 9. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 7-2i ; б) z = -5; в) z = 3i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1= 7-4i и z2=7+4i. 3. Найдите модуль и аргумент комплексного числа z =  - - i i 4. Запишите число z =5+5i в тригонометрической и показательной формах.
|
Вариант 10. 1. Изобразите геометрически на плоскости следующие комплексные числа: а) z = 6+i ; б) z = 1; в) z = -5i . 2. Выполните действия z1+z2, z1-z2, z1z2, z1:z2 над комплексными числами z1= 12+9i и z2=3-61i. 3. Найдите модуль и аргумент комплексного числа z =  -3i. -3i. 4. Запишите число z = -4+4i в тригонометрической и показательной формах. |
3. Ответить на контрольные вопросы:
1. Что такое главный аргумент комплексного числа?
2. Геометрическая интерпретация комплексного числа, множество комплексных чисел?
3. Какие правила действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление) вы знаете?
4. Как выглядит тригонометрическая форма комплексного числа?
5. Как выглядит показательная форма комплексного числа?
Практическая работа 5. Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей
Цель: закрепить и усовершенствовать практические приемы вычисления предела функции, раскрытие неопределенностей 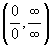 , раскрытие других видов неопределённости; вычисление предела многочлена и отношения многочленов (при x → 0, x → x0). Повторить и систематизировать знания по данной теме.
, раскрытие других видов неопределённости; вычисление предела многочлена и отношения многочленов (при x → 0, x → x0). Повторить и систематизировать знания по данной теме.
Теоретический материал, примеры вычисления пределов
Определение
Конечное число A называется пределом функции f(x) в точке x0, если для любого положительного числа ε можно указать такое положительное δ = δ(ε), что для всех значений x, удовлетворяющих неравенству 0 x− x0| f(x) − A| 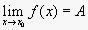
Свойства пределов функций:
Если функция имеет конечный предел, то он единственный.
Постоянный множитель можно выносить за знак предела

Предел суммы (или разности) функций равен сумме (или разности) их пределов, если оба предела являются конечными
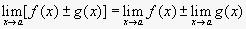
Предел произведения функций равен произведению их пределов, если оба предела являются конечными

Предел отношения функций равен отношению их пределов, если оба предела являются конечными и знаменатель не обращается в нуль

Вычисление несложных пределов
1. Найти предел функции 
Решение:
| Имеем неопределенность вида | 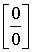
|
Для ее раскрытия разложим числитель и знаменатель на множители и сократим на общий множитель x + 2, который при x → -2 не равен нулю. В результате неопределенность будет раскрыта.

2. Найти предел функции 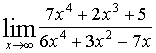
Решение:
| Имеем неопределенность вида | 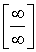
|
Для ее раскрытия можно либо разделить числитель и знаменатель на наибольшую степень переменной x и учитывая, что величина обратная бесконечно большой величине есть бесконечно малая величина, раскроем исходную неопределенность, либо вынести переменную в наибольшей степени в числители и знаменатели дроби и сократить на наибольшую степень.
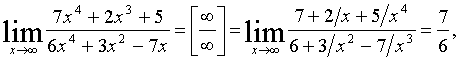
или

3. Найти предел функции 
Решение:
| Имеем неопределенность вида | 
|
Раскрываем ее аналогично тому, как это сделано в примере 2.

4. Найти предел функции 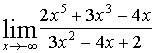
Решение:
| Имеем неопределенность вида  |
Раскрываем ее аналогично тому, как это сделано в примере 2.
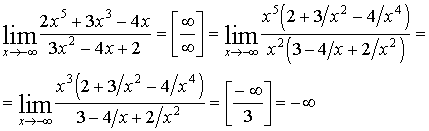
5. Найти предел функции 
Решение:
| В данном случае имеем неопределённость вида | 
|
Для её раскрытия можно использовать свойство, что существенно упростит вычисление предела, в отличии от примеров 2,3,4, хотя их можно тоже вычислить, используя данное свойство.
| Пусть дана дробно-рациональная функция | 
| , |
где P(x) и Q(x) некоторые многочлены. Тогда:
Если степень многочлена P(x) больше степени многочлена Q(x), то 
Если степень многочлена P(x) меньше степени многочлена Q(x), то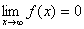
Если степень многочлена P(x) равна степени многочлена Q(x), то 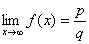 ,
,
где p, q числовые коэффициенты при наивысших степенях x в данных многочленах.
В данном случае степени числителя и знаменателя равны двум, поэтому
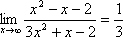
6. Найти предел функции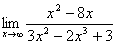
Решение:
| В данном случае снова имеем неопределённость вида | 
|
Для её раскрытия используем то же известное свойство, что и в предыдущем случае. Степень числителя равна двум, а степень знаменателя – трём. Поэтому

7. Найти предел функции 
Решение:
| Имеем неопределенность вида | 
|
Для ее раскрытия умножим числитель и знаменатель на выражение сопряженное числителю, разложим выражение, стоящее в знаменателе, на множители по формуле разности кубов и сократим числитель и знаменатель на общий множитель x - 4, который при x → 4 не равен нулю. В результате неопределенность будет раскрыта.

8. Найти предел функции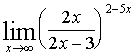
Решение:
| Имеем неопределенность вида | 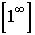
|
| Для раскрытия этой неопределенности воспользуемся вторым замечательным пределом | 
|

9. Найти предел функции 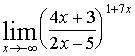
Решение:
В данном примере при выяснении вида неопределенности видим, что таковой не имеется.
| Имеем | 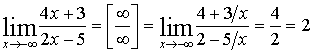
| , тогда |
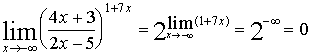
Задания для самостоятельной работы
| Вариант 1 | Вариант 2 |
| Найдите предел функции: 1)  ; ; 2) 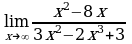 ; ; 3)  ; ; 4)  ; ; 5)  ; ; 6) 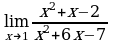 7)  8) 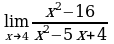 9) 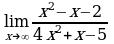 10)  11) 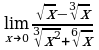 12)  13)  14)  15)  16) 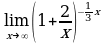 17) 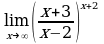 18)  19)  20)  | Найдите предел функции: 1)  ; ; 2) 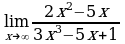 ; ; 3)  ; ; 4)  ; ; 5) 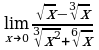 ; ; 6)  7)  8)  9)  10)  11)  12)  13) 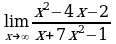 14) 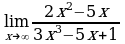 15)  16) 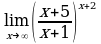 17)  18) 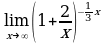 19)  20)  |
Контрольные вопросы:
Что называется пределом функции?
Каким образом определяется число е?
Сформулируйте основные теоремы вычисления пределов.
Запишите формулы соответствующие первому и второму замечательным пределам.
Какие приемы используются при раскрытии неопределенностей?
Практическая работа 6. Вычисление односторонних пределов, классификация точек разрыва
Цель: сформировать умение исследовать функцию на непрерывность и наличие точек разрыва, определять род точек разрыва.
Теоретическая часть
Функция 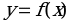 называется непрерывной
называется непрерывной
в точке х0, если она: 1) определена в точке х0; 2) имеет конечный предел при 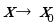 ; 3) этот предел равен значению функции в этой точке
; 3) этот предел равен значению функции в этой точке 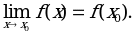
Функция называется непрерывной, если:
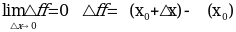
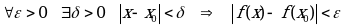

Функция называется непрерывной на некотором промежутке Х, если она непрерывна в каждой точке этого промежутка.
Пример: Доказать, что функция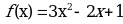 непрерывна на (-∞;+∞)
непрерывна на (-∞;+∞)
Решение: 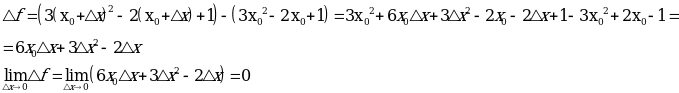
Определение. Точка  , в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
, в которой нарушено хотя бы одно из трех условий непрерывности функции, а именно:
называется точкой разрыва функции.
Пример
Функция 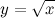 не определена в точке
не определена в точке  , а значит, эта точка является точкой разрыва указанной функции.
, а значит, эта точка является точкой разрыва указанной функции.
Определение. Если в точке  существуют конечные пределы
существуют конечные пределы 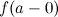 и
и  , такие, что
, такие, что  , то точка
, то точка  называется точкой разрыва первого рода.
называется точкой разрыва первого рода.
Пример
Функция 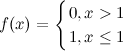 в точке
в точке 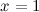 имеет разрыв первого рода, так как
имеет разрыв первого рода, так как
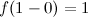 , а
, а 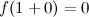
Определение. Если хотя б один из пределов 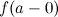 или
или  не существует или равен бесконечности, то точка
не существует или равен бесконечности, то точка  называется точкой разрыва второго рода.
называется точкой разрыва второго рода.
Пример
Для функции  точка
точка  - точка разрыва второго рода, так как
- точка разрыва второго рода, так как  .
.
Определение. Если существуют левый и правый пределы функции в точке и они равны друг другу, но не совпадают со значением функции  в точке
в точке  :
: 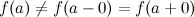 или функция
или функция  не определена в точке
не определена в точке  , то точка
, то точка  называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Пример
Рассмотрим функцию  . Найдем односторонние пределы и значение функции в точке
. Найдем односторонние пределы и значение функции в точке  :
:


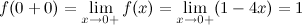
Так как  и не равны значению функции в точке, то точка
и не равны значению функции в точке, то точка  - точка устранимого разрыва.
- точка устранимого разрыва.
Примеры решения задач
Задание. Исследовать функцию 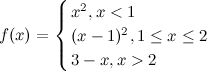 на непрерывность.
на непрерывность.
Решение. Рассматриваемая функция определена и непрерывна на промежутках  ,
,  и
и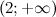 , на которых она задана непрерывными элементарными функциями
, на которых она задана непрерывными элементарными функциями  ,
, и
и  соответственно. А тогда, разрыв возможен только на концах указанных промежутков, то есть в точках
соответственно. А тогда, разрыв возможен только на концах указанных промежутков, то есть в точках 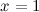 и
и 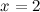 .
.
Найдем односторонние пределы и значение функции в каждой из точек.
1) Рассмотрим точку 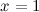 . Для нее
. Для нее
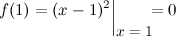

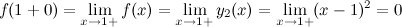
Так как  , то в точке
, то в точке 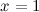 функция терпит разрыв первого рода.
функция терпит разрыв первого рода.
2) Для точки 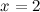 имеем:
имеем:


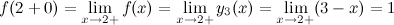
Так как односторонние пределы и значение функции в этой точке равны, то это означает, что в точке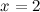 функция непрерывна.
функция непрерывна.
Ответ. В точке 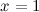 функция терпит разрыв первого рода, а в точке
функция терпит разрыв первого рода, а в точке 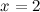 непрерывна.
непрерывна.
Задание. Исследовать функцию 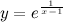 на непрерывность в точках
на непрерывность в точках  и
и  .
.
Решение. 1) Исследуем функцию на непрерывность в точке  :
:
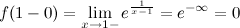

Так как один из односторонних пределов бесконечен, то точка  - точка разрыва второго рода.
- точка разрыва второго рода.
2) Для точки  получаем:
получаем:

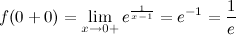
и значение функции в точке

Таким образом, в точке  заданная функция является непрерывной.
заданная функция является непрерывной.
Ответ.  - точка разрыва второго рода, а в точке
- точка разрыва второго рода, а в точке  функция непрерывна.
функция непрерывна.
Пример
Найти точки разрыва функции и установить их тип

Содержание практической работы
Задание 1. Доказать, что функция является непрерывной
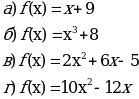
Задание 2. Найти точки разрыва и установить их тип
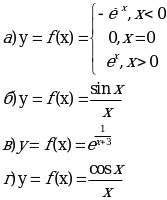
Практическая работа 7. Вычисление производных сложных функций
Цель работы: закрепить навык вычисления производной функции.
Необходимо знать: приемы и правила дифференцирования функций.
Необходимо уметь: вычислять производную простой и сложной функций, применяя таблицу правил и формул дифференцирования.
1.Теоретическая часть.
Производная функции y=y(x) определяется по формуле: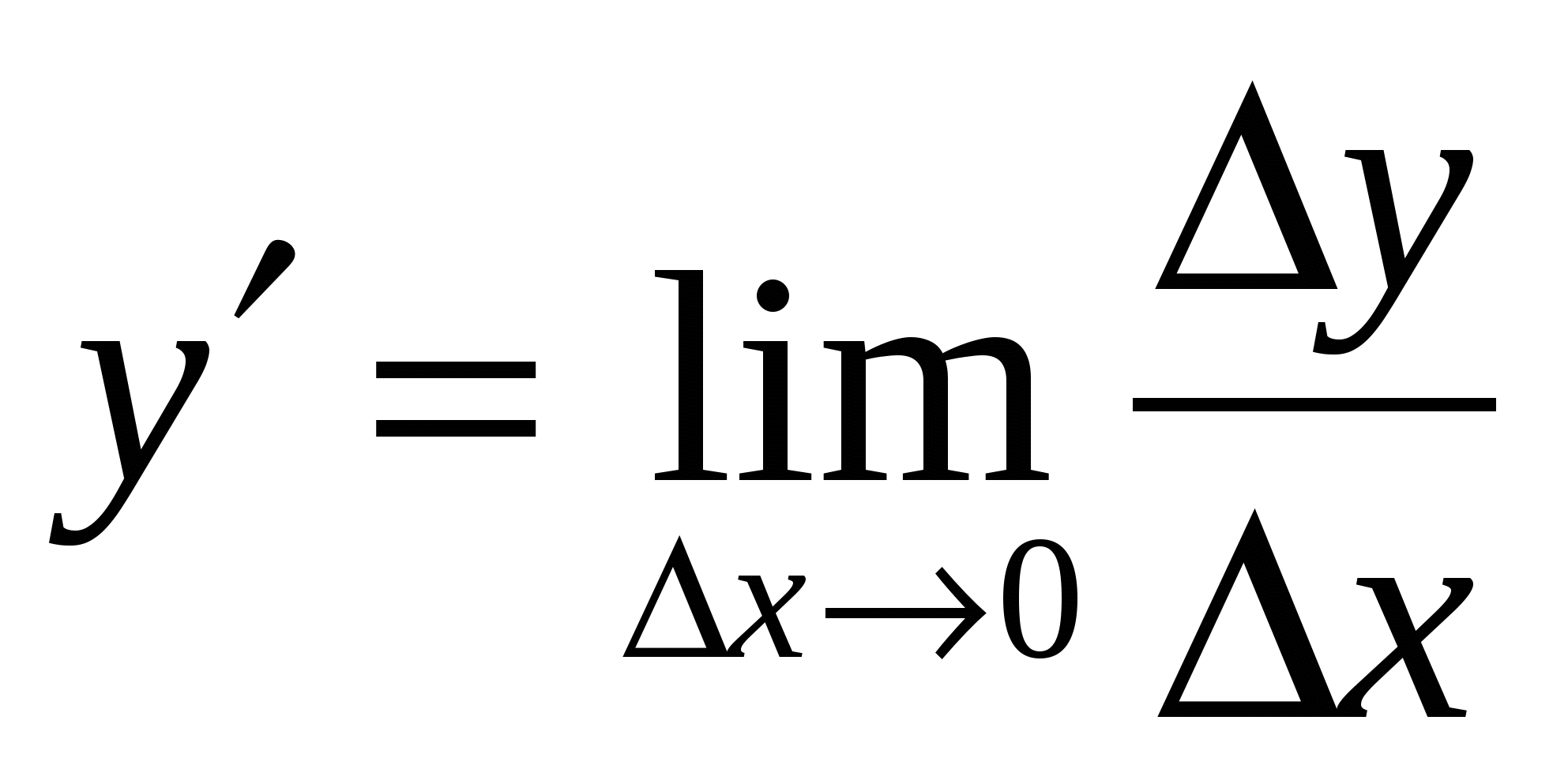
Правила:
Формулы
1) 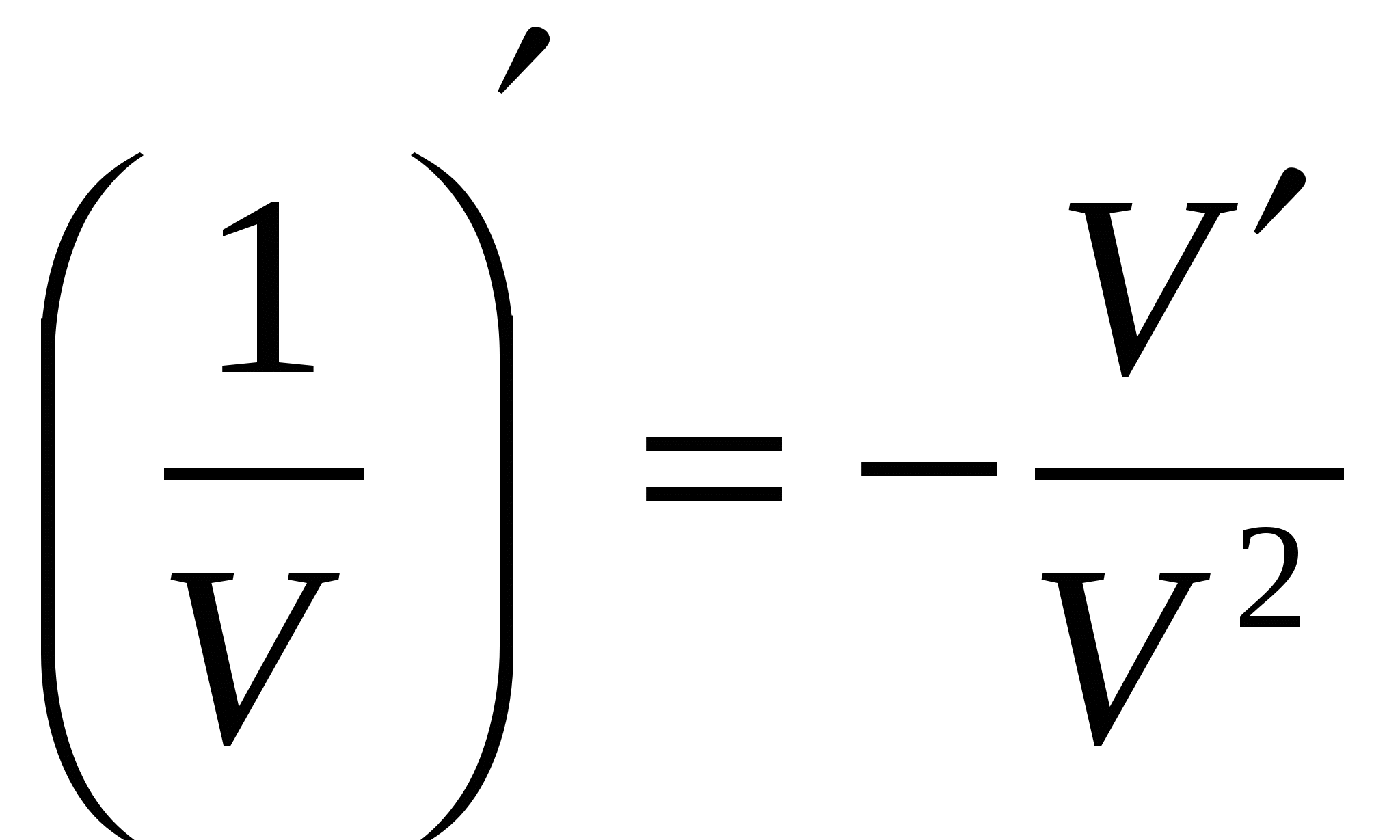 1)
1) 
2) 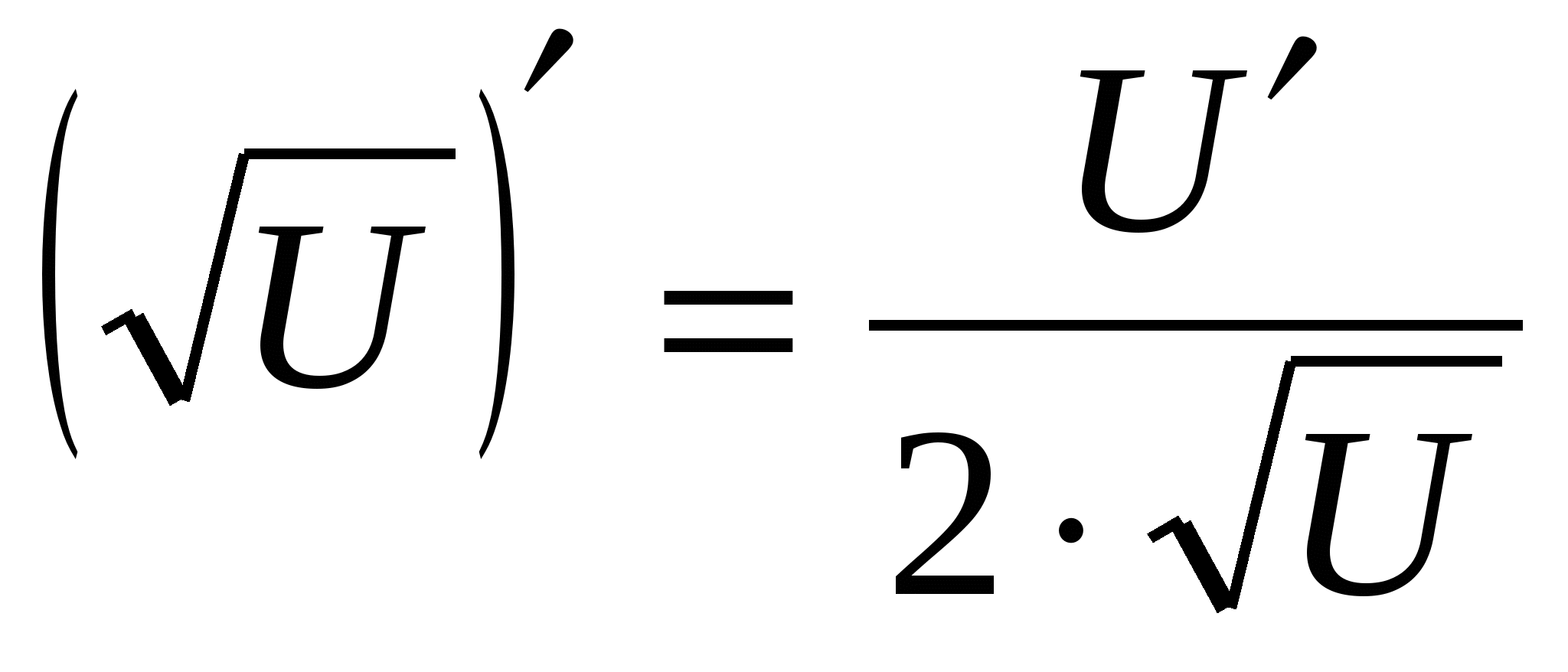 2)
2) 
3)  3)
3) 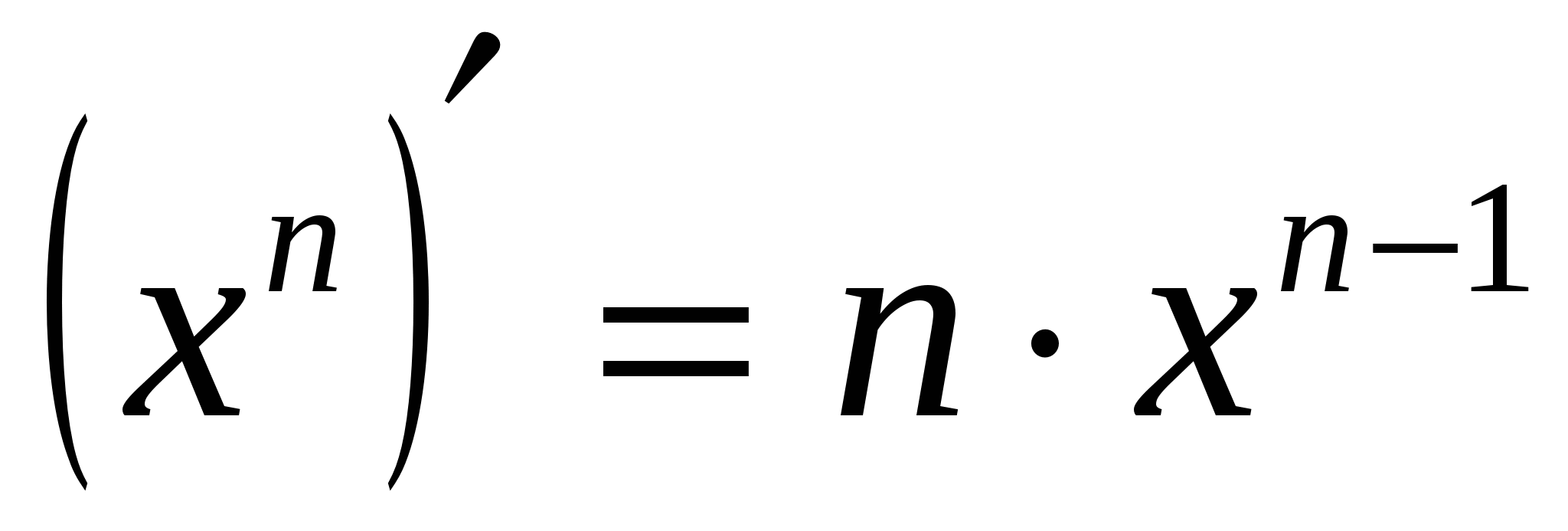
4) 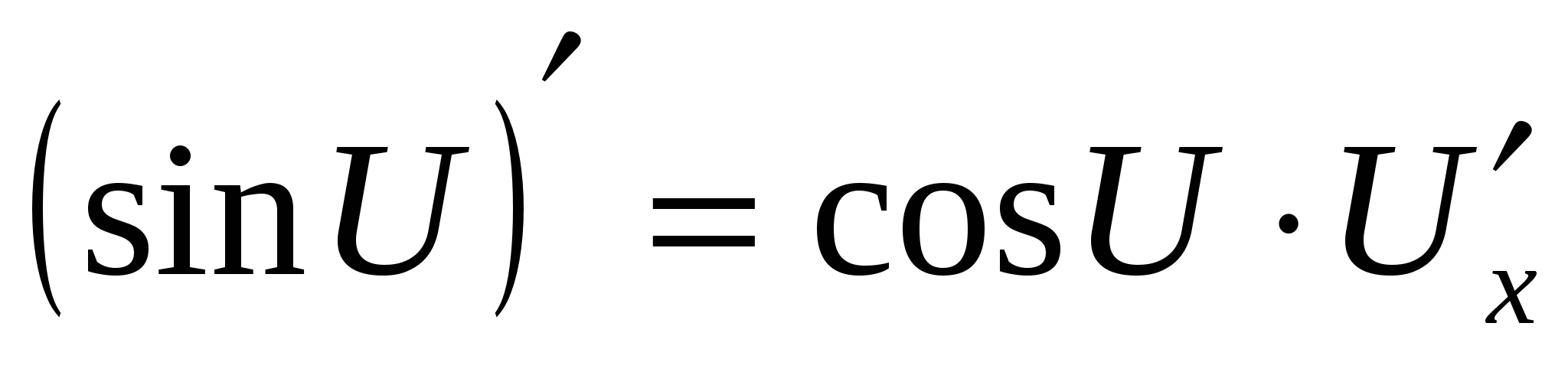 4)
4) 
5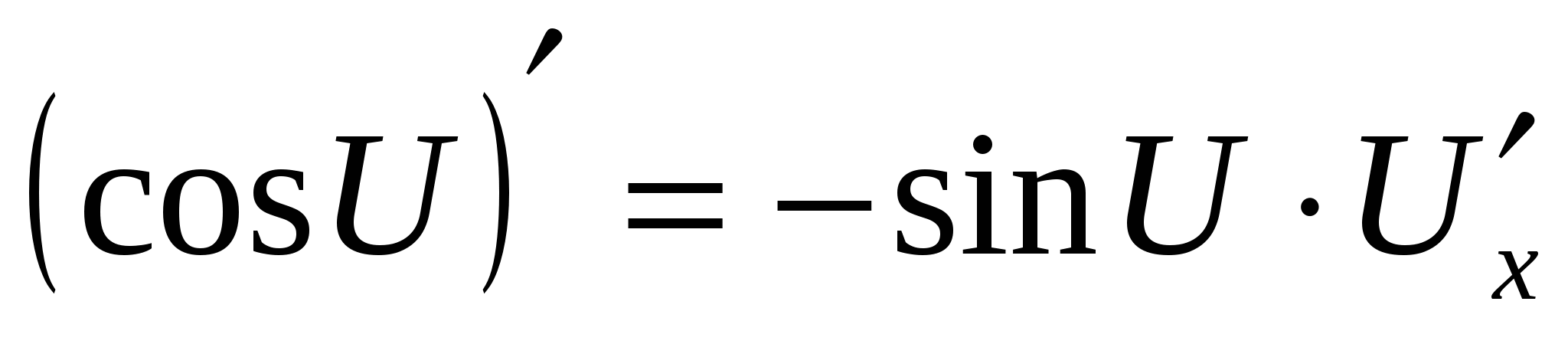 5
5 
6  6
6 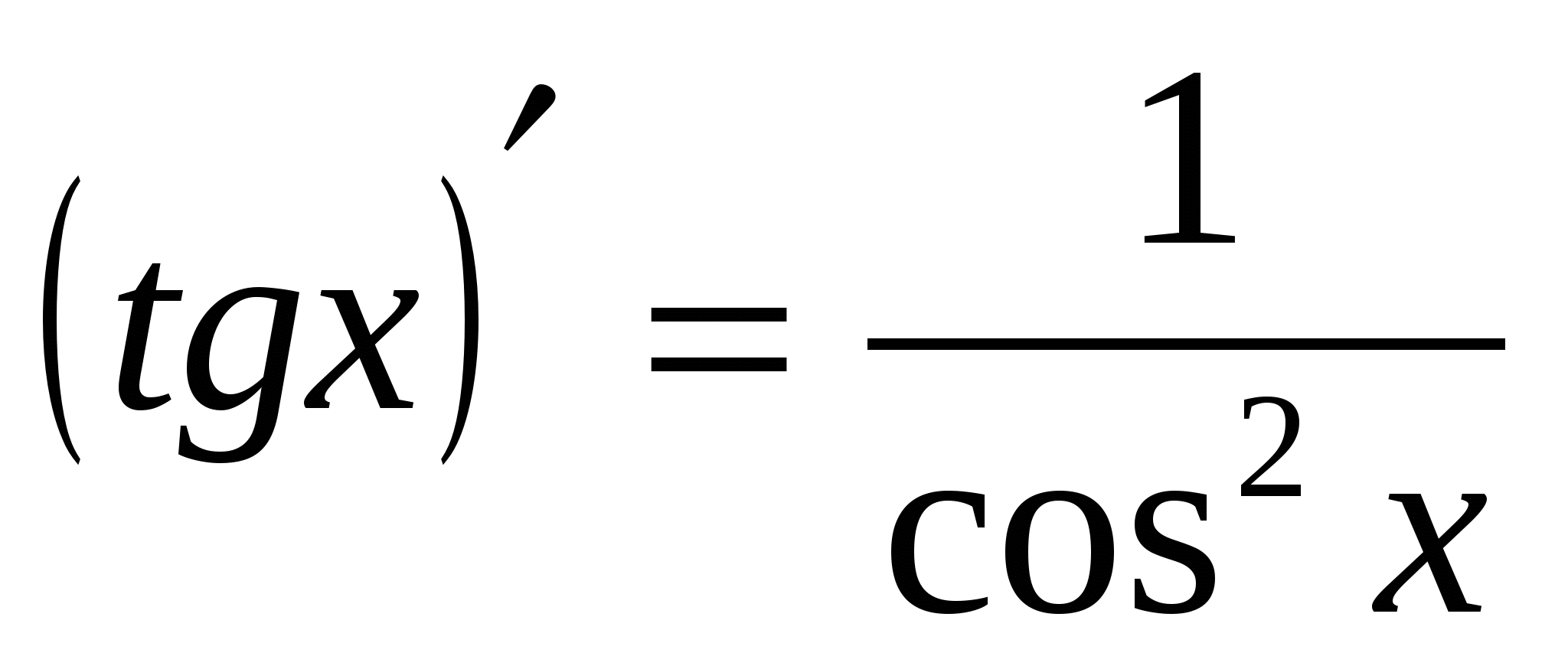

7 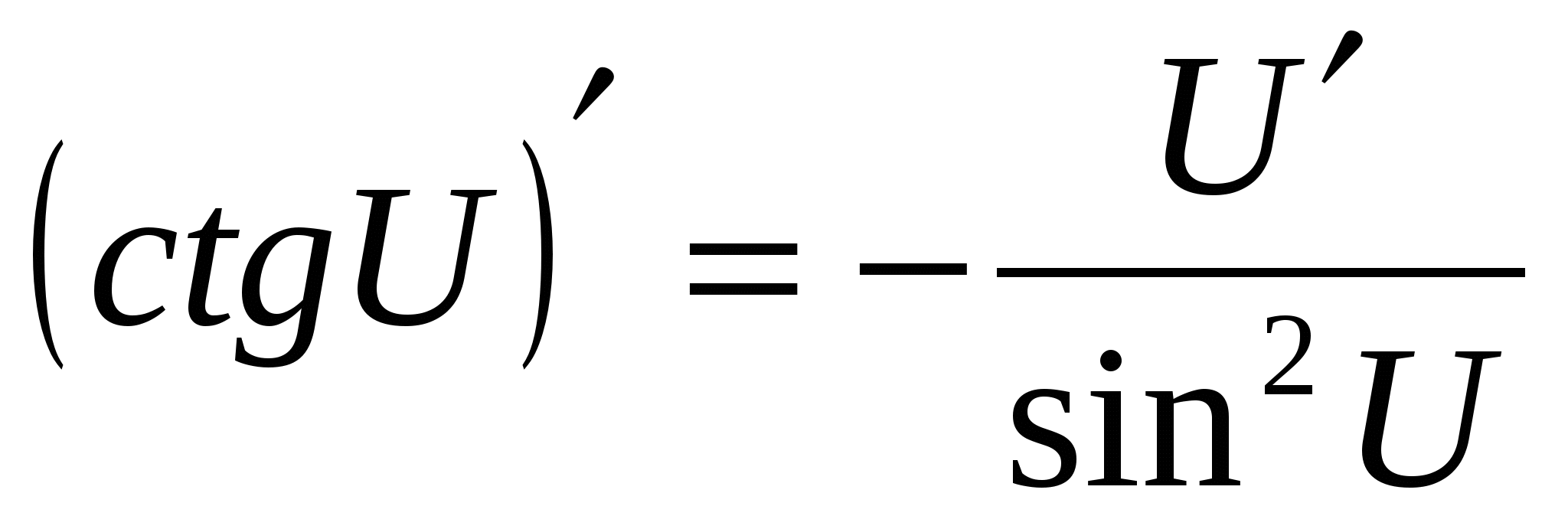 7
7 
8  8
8 
9 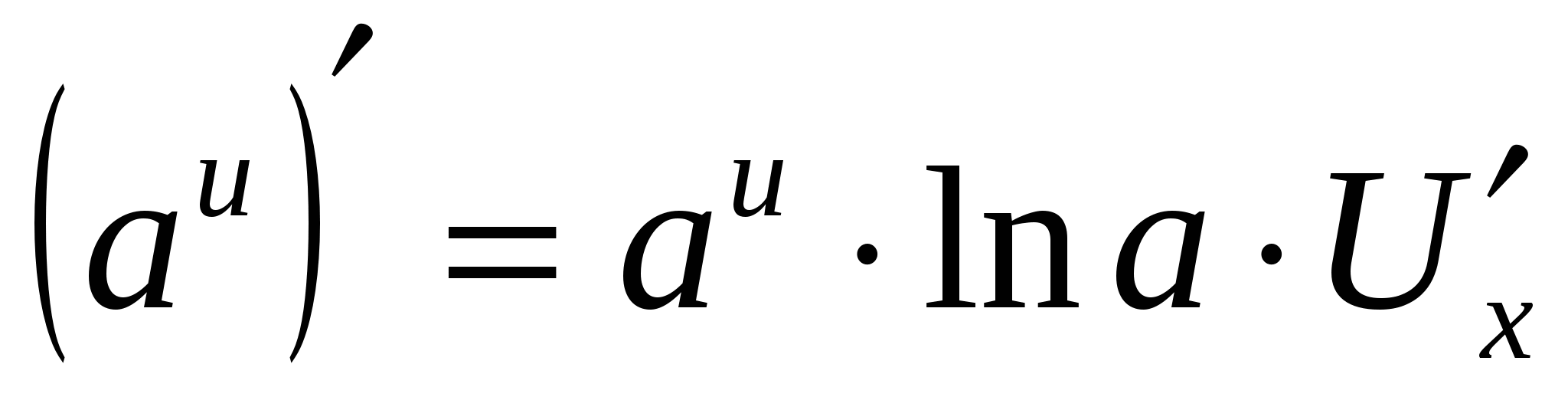 9
9 
10  10
10 
11 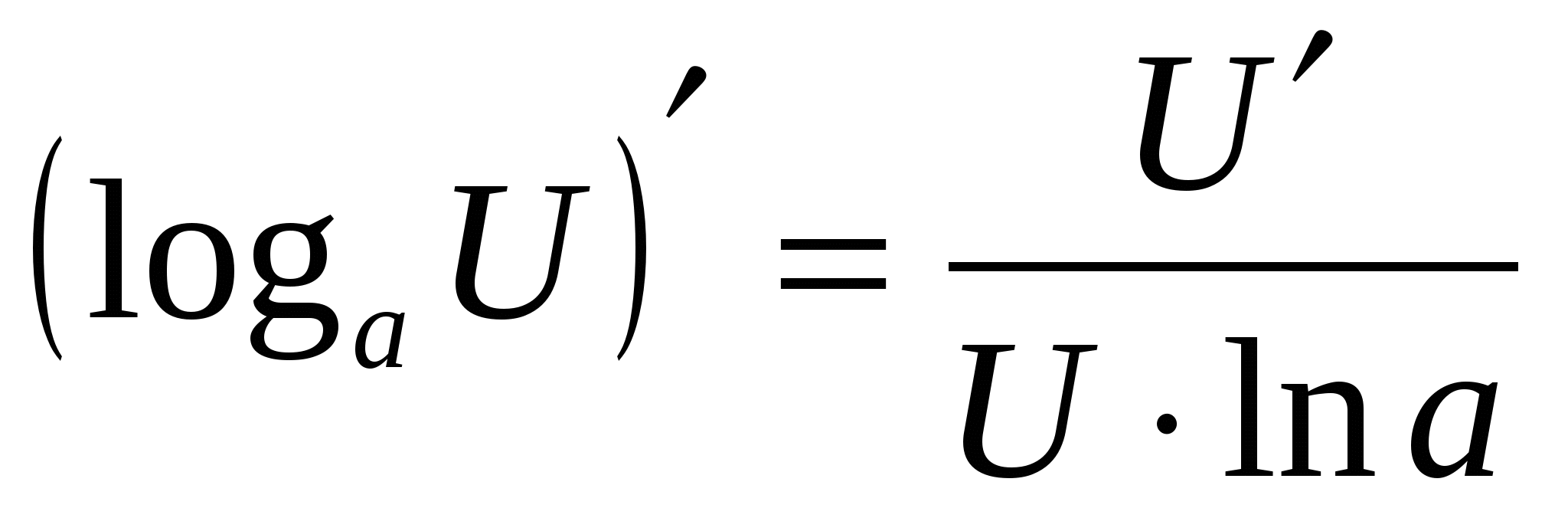 11
11


Приёмы вычисления производной
Пример 1. Найти производную функции  .
.
Решение: - применим правила (2) и (4) 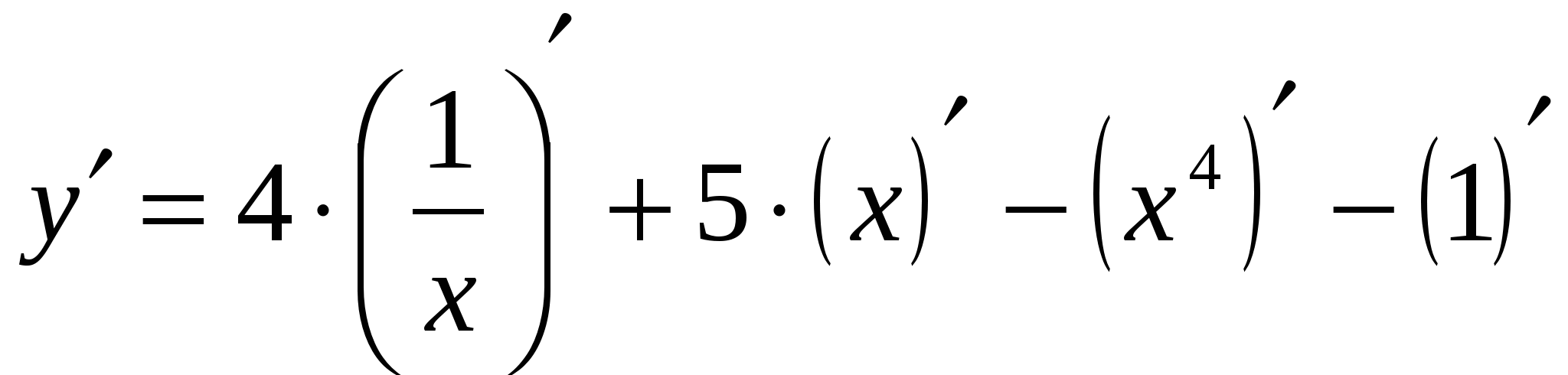
- по формулам (1), (3) , а так же по правилам (1) и (5) получаем
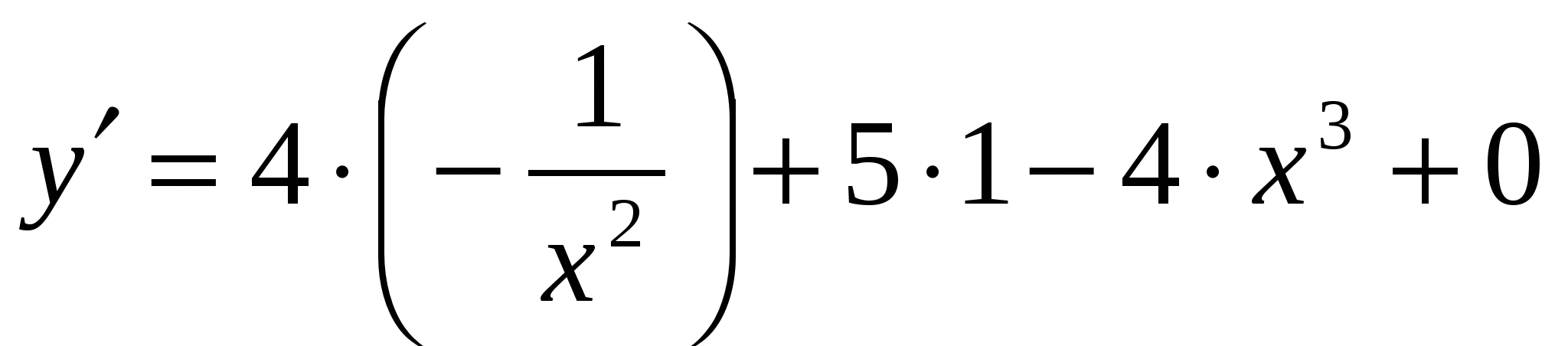
- после упрощения производная примет вид  .
.
Пример 2. Найти производную функции 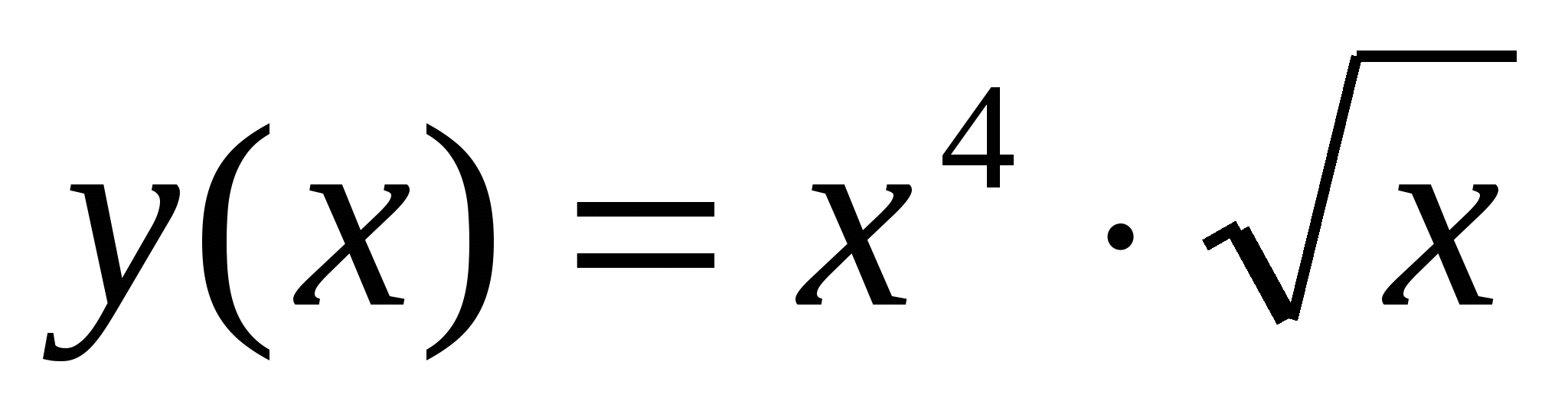
Решение: - преобразовать по свойствам степени 
- по формуле (3) найти производную при 
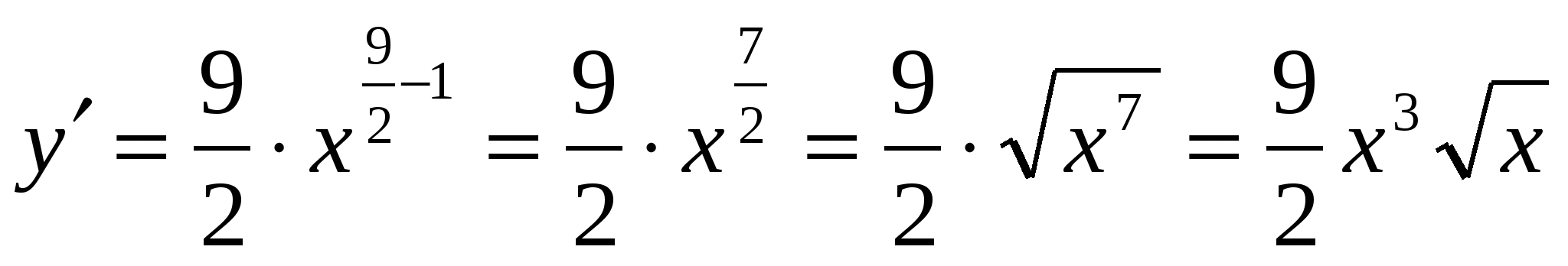 ( воспользовались формулой
( воспользовались формулой  )
)
Пример 3. Найти производную функции 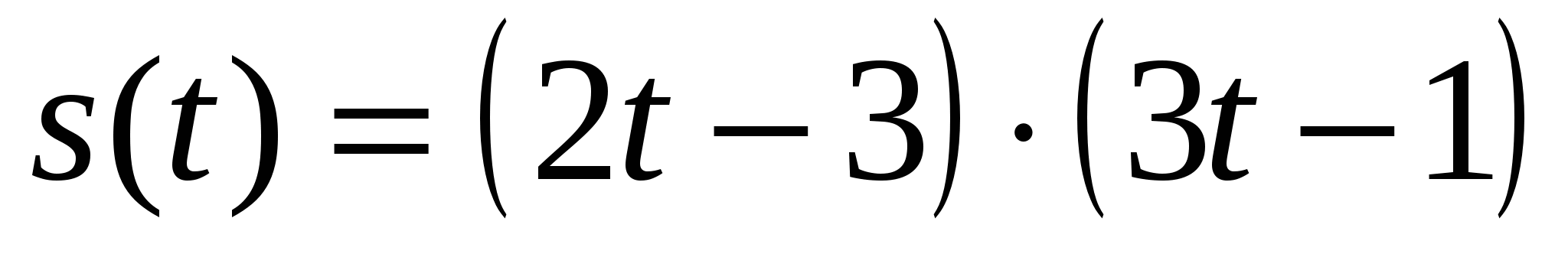 .
.
Решение: - по правилу (3) имеем: 
- по правилу (6) примет вид: 
- после раскрытия скобок производная: 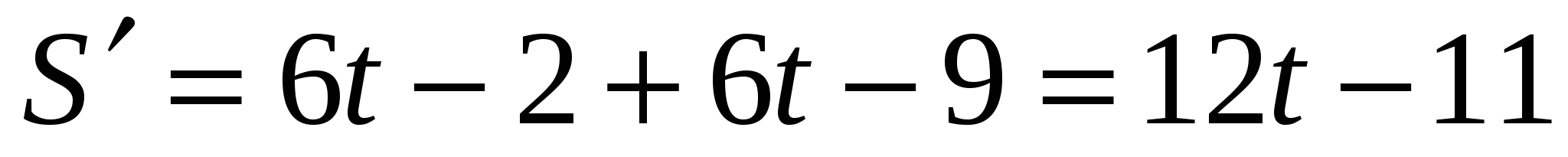
Этот пример можно решить иначе:
- открыть скобки и упростить 

- применить правила (2) и(4) 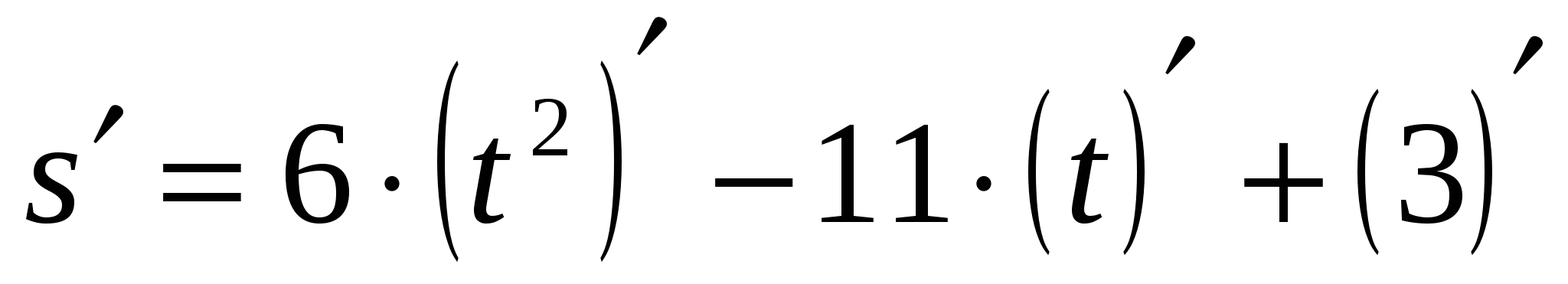
- по формуле (3) и по правилам (1) и (5) получим:

Пример 4. Найти производную функции 
Решение: - применить правило (7) 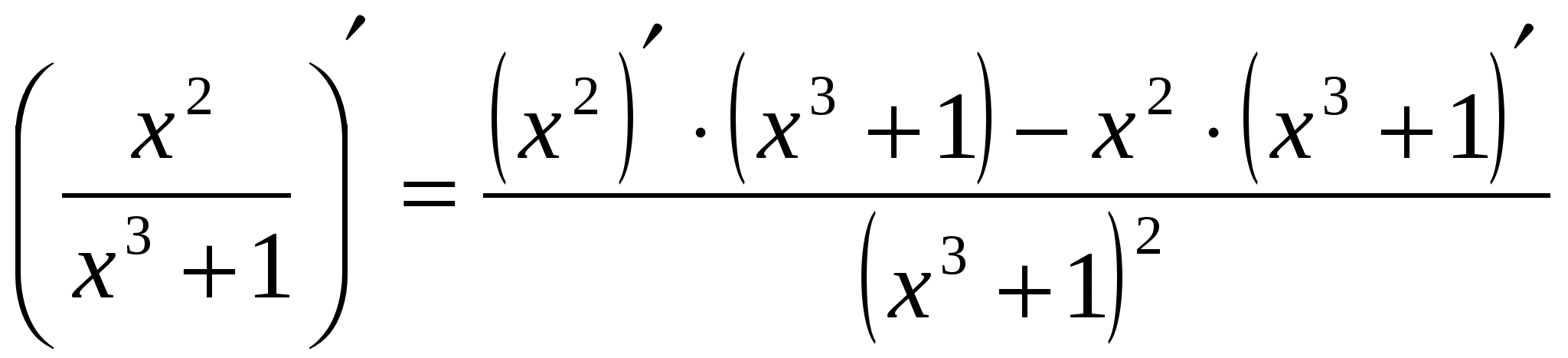
- применить правило суммы (2) и формулу (3) вычисления производной

Пример 5. Найти производную функции 
Решение: данная функция является сложной; положим  . Согласно формуле (2)
. Согласно формуле (2) 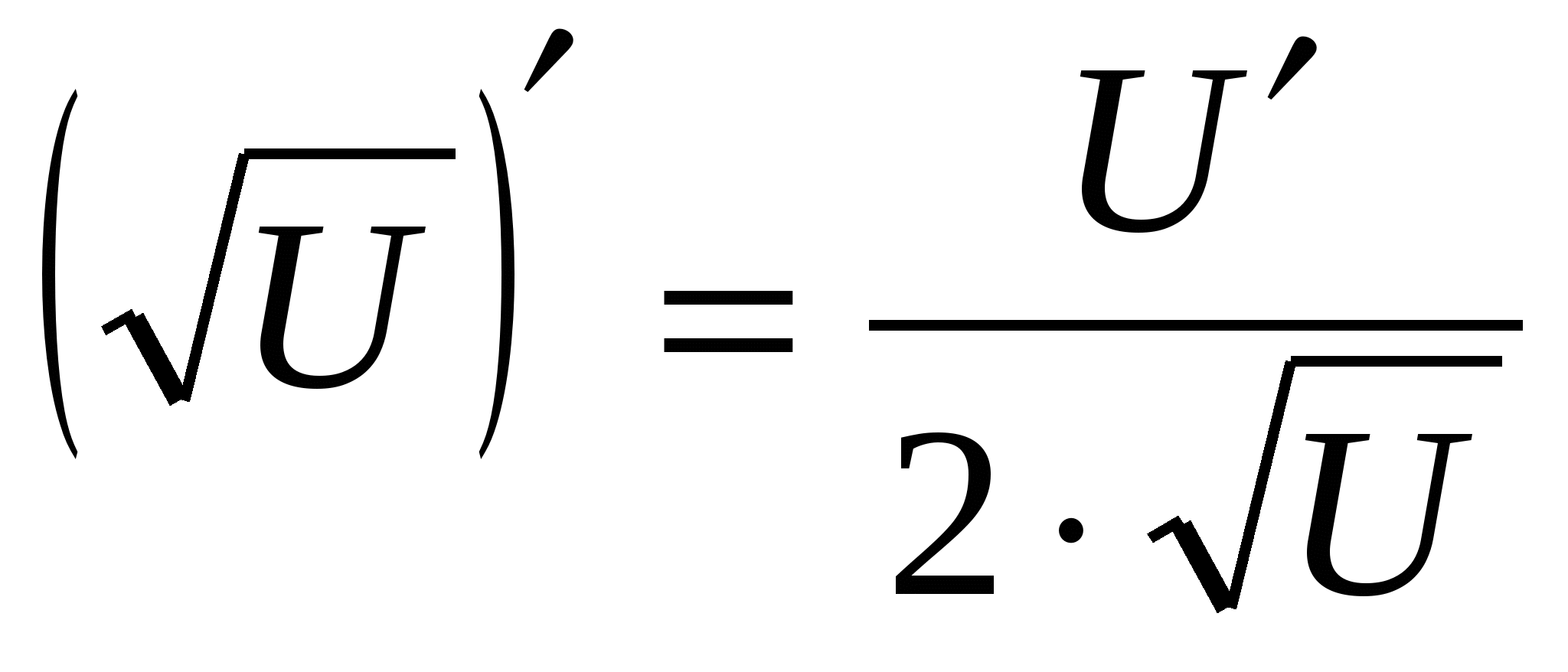 , получаем
, получаем 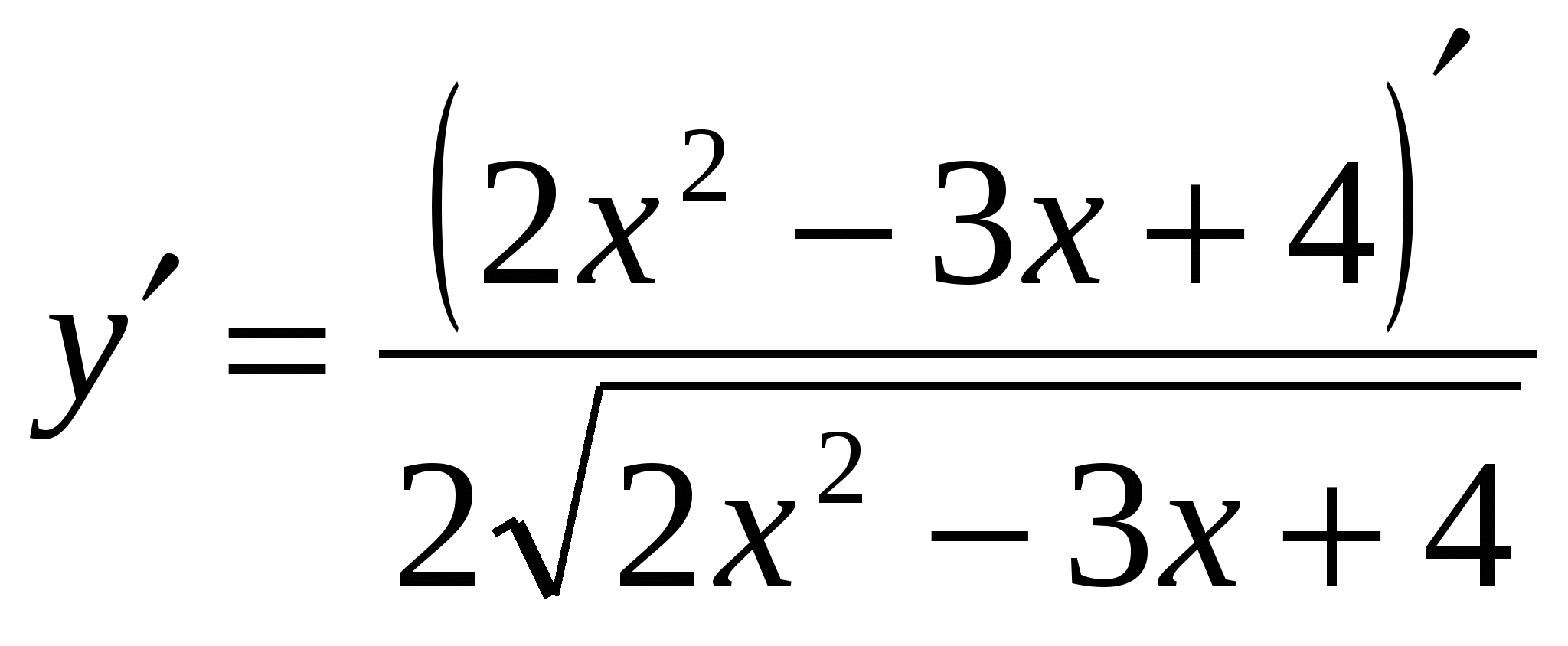 . Применим правила (2) и (4):
. Применим правила (2) и (4):  . По формуле (3) имеем:
. По формуле (3) имеем: 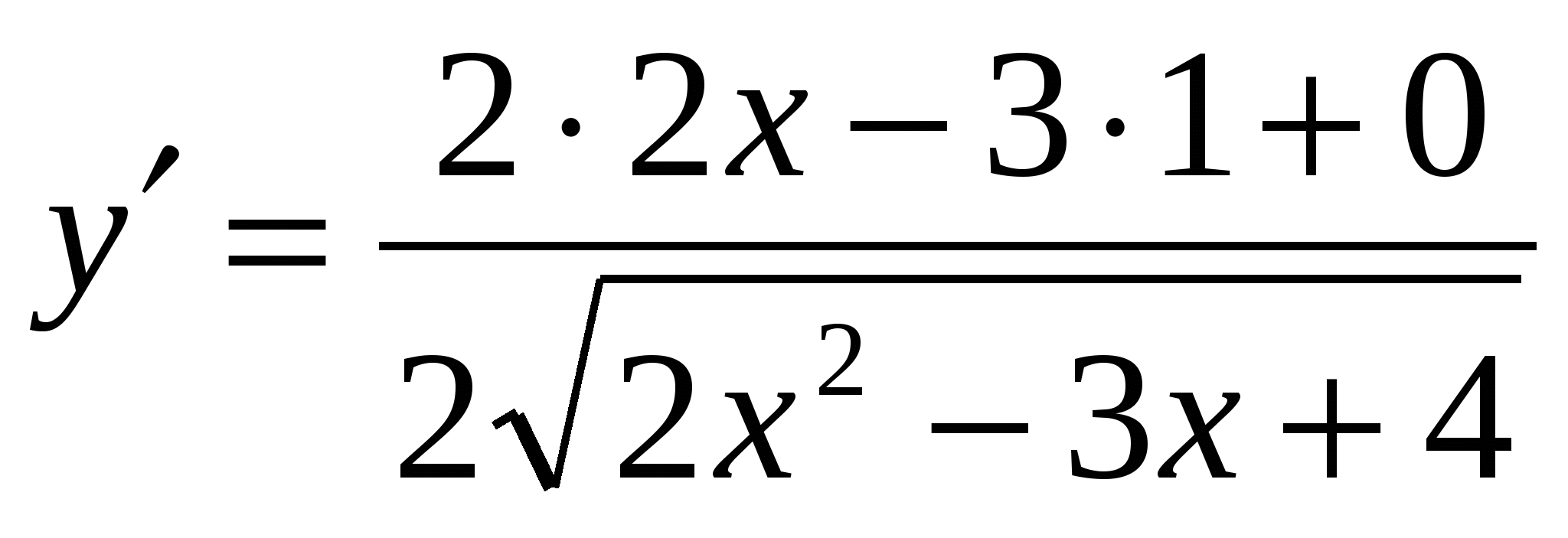 . После упрощения примет вид:
. После упрощения примет вид:  .
.
Пример 6. Найти производную функции 
Решение: - применить правило (4) и формулу сложной функции (4)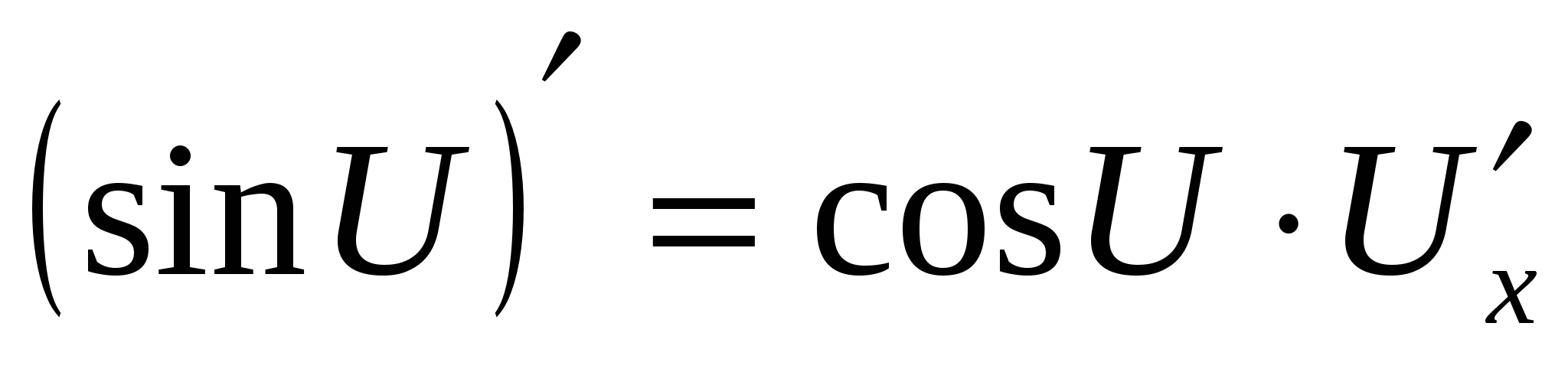 , где
, где , тогда
, тогда 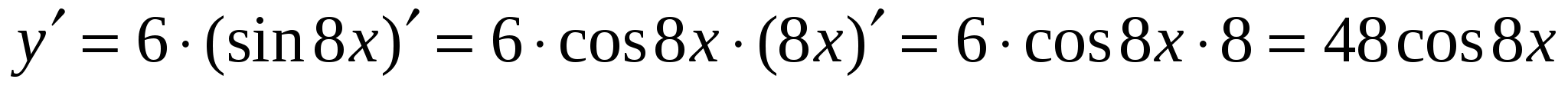
Самостоятельная работа
Контрольные вопросы
Запишите правило вычисления производной произведения двух функций.
Запишите правило вычисления производной частного двух функций.
Дополните фразу: «Постоянный сомножитель можно … за знак производной».
Практическая работа 8. Дифференциал функции. Приближенные вычисления
Теоретические сведения, методические рекомендации
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х. (1)
Дифференциал dу называют также дифференциалом первого порядка.
Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у'=х'=1, то, согласно формуле (1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (1) можно записать так:
dy=ƒ'(х)dх, (2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2) следует равенство  .
.
Теперь производную можно рассматривать как отношение дифференциалов dy и dх.
Основные теоремы о дифференциалах
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции (dy=f'(x)dx) и соответствующие теоремы о производных.
Теорема. Дифференциал суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами:

Пример1. Найти дифференциал функции ƒ(х)=3x2-sin(l+2x).
Решение: По формуле dy=ƒ'(х) dx находим
dy=(3х2-sin(l+2x))'dx=(6х-2cos(l+2х))dx.
Пример2. Найти дифференциал функции  Вычислить dy при х=0, dx=0,1.
Вычислить dy при х=0, dx=0,1.
Решение:
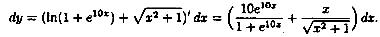
Подставив х=0 и dx=0.1, получим

Ответ: 0,5
Применение дифференциала к приближенным вычислениям
1) Как уже известно, приращение ∆у функции у=ƒ(х) в точке х можно представить в виде ∆у=ƒ'(х)•∆х+α•∆х, где α→0 при ∆х→0, или ∆у=dy+α•∆х. Отбрасывая бесконечно малую α•∆х более высокого порядка, чем ∆х, получаем приближенное равенство
∆у≈dy, (3)
причем это равенство тем точнее, чем меньше ∆х.
Это равенство позволяет с большой точностью вычислить приближенно приращение любой дифференцируемой функции.
Дифференциал обычно находится значительно проще, чем приращение функции, поэтому формула (3) широко применяется в вычислительной практике.
Пример 3. Найти приближенное значение приращения функции у=х3-2х+1 при х=2 и ∆х=0,001.
Решение: Применяем формулу (3): ∆у≈dy=(х3-2х+1)'•∆х=(3х2-2)•∆х.

Ответ: 0,01
2) Для вычислений приближенных значений функций используется формула
ƒ(х+∆х)≈ƒ(х)+ƒ'(х)•∆х. (4)
Пример 4. Вычислить приближенно arctg(1,05).
Решение: Рассмотрим функцию ƒ(х)=arctgx. По формуле (4) имеем:
arctg(x+∆х)≈arctgx+(arctgx)'•∆х, т. е.

Так как х+∆х=1,05, то при х=1 и ∆х=0,05 получаем:
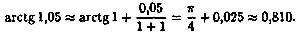
Ответ: 0,810
Самостоятельная работа
Найти дифференциал функции:
а) у=(1-х2)5; б) у=х3 – е3х+5
Найти приближенное значение приращения функции у=х4+5х-10 при х=2 и ∆х=0,001.
Найти приближенное значение f(4,001), если f(x)=х3-5х2+80
Практическая работа 9. Применение производной для исследования функции и построения графика
Цель: научиться применять производную второго порядка к исследованию графика функции на выпуклость и перегиб.
Краткая теоретическая справка
Кривая  называется выпуклой в промежутке
называется выпуклой в промежутке  , если она лежит ниже касательной в любой точке этого промежутка.
, если она лежит ниже касательной в любой точке этого промежутка.
Кривая  называется вогнутой в промежутке
называется вогнутой в промежутке  , если она лежит выше касательной в любой точке этого промежутка
, если она лежит выше касательной в любой точке этого промежутка
Выпуклость кривой, являющейся графиком функции  , характеризуется знаком её второй производной: если в некотором промежутке
, характеризуется знаком её второй производной: если в некотором промежутке  , то кривая вогнута в этом промежутке; если же
, то кривая вогнута в этом промежутке; если же 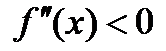 , то кривая выпукла в этом промежутке.
, то кривая выпукла в этом промежутке.
Точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот, называется точкой перегиба.
Если в точке перегиба x0 существует вторая производная f ''( x0 ), то  .
.
Теорема. Пусть  дифференцируема на промежутке
дифференцируема на промежутке  . Если во всех точках промежутка
. Если во всех точках промежутка  вторая производная функции y=f(x) отрицательная, т.е.
вторая производная функции y=f(x) отрицательная, т.е. 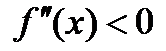 , то график функции на этом промежутке выпуклый, если же
, то график функции на этом промежутке выпуклый, если же  – вогнутый.
– вогнутый.
Практические задания
Найдите интервалы выпуклости и точки перегиба графика функции.
Для аудиторной работы
а)  ; б)
; б) 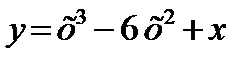 ; в)
; в)  ; г)
; г)  .
.
Для самостоятельной работы
Вариант 1
а) 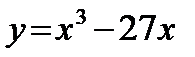 ; б)
; б) 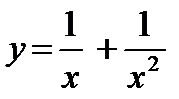 ; в)
; в) 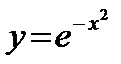 .
.
Вариант 2
а) 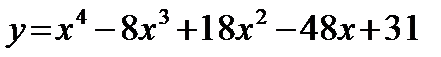 ; б)
; б)  ; в)
; в) 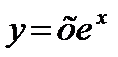 .
.
Вариант 3
а) 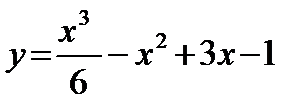 ; б)
; б) 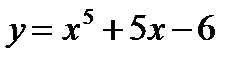 ; в)
; в) 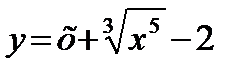 .
.
Вариант 4
а)  ; б)
; б)  ; в)
; в) 
Контрольные вопросы
1. Понятие выпуклости функции.
2. Понятие точки перегиба функции.
3. Как с помощью второй производной определить характер выпуклости функции.
Практическая работа 10. Вычисление неопределенного интеграла
Цель занятия: отработка навыков вычисления неопределенного интеграла.
Задачи занятия: научиться вычислять неопределенный интеграл при помощи таблицы интегралов, развитие вычислительных навыков, логического мышления.
Теоретические сведения необходимые для выполнения практического задания
Понятия первообразной и ее основные свойства.
Основные правила вычисления первообразной.
Неопределенный интеграл, его свойства.
Таблица неопределенных интегралов.
Основные правила вычисления неопределенного интеграла.
Методы интегрирования.
| Вариант 1 Вычислить неопределенный интеграл
|
Вариант 2 Вычислить неопределенный интеграл |


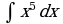


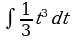

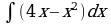
| 






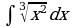
| 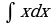


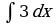
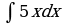
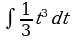

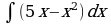
| 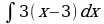
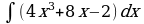


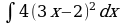


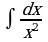
|
| Вариант 3 Вычислить неопределенный интеграл | Вариант 4 Вычислить неопределенный интеграл |
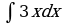



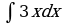
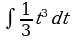

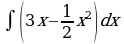
| 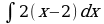


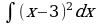
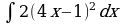



| 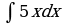


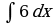

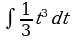
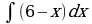
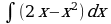
| 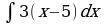
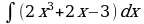
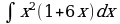
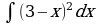
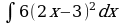



|
| Вариант 5 Вычислить неопределенный интеграл
|
Вариант 6 Вычислить неопределенный интеграл |


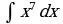

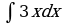



| 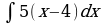

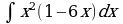

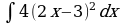


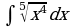
| 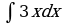







| 
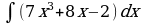




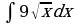
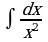
|
Критерии оценивания
Каждый пример оценивается в 1 балл. Максимальное количество баллов за правильно выполненные примеры 16 баллов.
9 баллов оценка «3», 12 баллов оценка «4», 15 баллов оценка «5».
Практическая работа 11. Приложение определённого интеграла к решению прикладных задач
Цель: научиться определять форму полученной фигуры в сравнении с криволинейной трапецией, аналитически выражать и вычислять площадь полученной фигуры.
Теоретический материал
Фигура, ограниченная снизу отрезком [a;b] оси Ох, сверху графиком непрерывной функции у = f(x), принимающей положительные значения, а с боков отрезками прямых х = а и х = b, называется криволинейной трапецией.
Вычисление площади такой фигуры являлось одной из причин введения определенного интеграла.

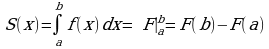
Площадь криволинейной трапеции является первообразной функции f(x). Функция F(x) называется первообразной функции отf(x) на некотором промежутке, если для всех х из этого промежутка выполняется условие: F`(x)=f(x).
Правила вычисления первообразных.
1) Первообразная суммы равна сумме первообразных.
2) Постоянный множитель можно вынести знак первообразной.
3) Если F(x) – первообразная для f(x) и k, b – постоянные, причём 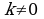 , то
, то 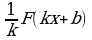 - первообразная для f(kx+b).
- первообразная для f(kx+b).

Алгоритм вычисления площади плоской фигуры:
Построение графиков функций, образующих данную фигуру.
Определение формы полученной фигуры в сравнении с криволинейной трапецией.
Аналитическое выражение площади полученной фигуры.
Вычисление площади полученной фигуры.
Образец решения задач
Найдите площадь фигуры, ограниченной осями координат, графиком функции 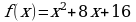 и прямой х = - 2.
и прямой х = - 2.
Решение.
1. Графиком функции 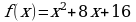 является парабола.
является парабола.
Вершина параболы  , где а = 1, b = 8:
, где а = 1, b = 8:
х0 = - 4
у0 = (-4)2 + 8*(-4) + 16 = 16 – 32 + 16 = 0
(- 4; 0) – вершина параболы
2. Найдём точки пересечения графика функции 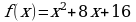 с осью Ох (у=0):
с осью Ох (у=0):
х = 0 – вершина параболы лежит на оси Ох.
3. Найдём точки пересечения графика функции 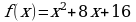 с осью Оу (х=0):
с осью Оу (х=0):
у = 02 +8*0 + 16 = 16
(0; 16) – точка пересечения параболы с осью Оу.

АВС – криволинейная трапеция, тогда
 , где
, где

а = - 4
b = - 2

Задание
Вычислите площадь фигуры, ограниченную линиями:
у=2х, х=2, х=5, у=0.
у=3-х, х=1, х=2, у=0.
у=9-х2, х=-1, х=2, у=0.
у=х2+5х+6, х=-1, х=2, у=0.
у=х2-6х+9, х=2, х=0, у=0.
у=х2-6х+10, х=-1, х=3, у=0.
Контрольные вопросы:
Сформулируйте определение криволинейной трапеции.
Сформулируйте определение первообразной.
Сколько первообразных может иметь каждая функция?
Каков алгоритм вычисления площади криволинейной трапеции?
Какие известны правила вычисления первообразных?
По какой формуле вычисляется площадь криволинейной трапеции?
Практическая работа 12. Решение дифференциальных уравнений первого порядка
Образец выполнения задания:
Пример 1. Решить дифференциальное уравнение 2dy = (3x – 4) dx. Найти частное решение при х=1, у=2.
Решение:
2dy = (3x – 4) dx
 =
= 
2у = 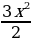 - 4х + С
- 4х + С
у = 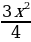 - 2х +
- 2х +  - общее решение
- общее решение
Если х=1, у=2, то 2 =  – 2 . 1 +
– 2 . 1 + 
2 =  – 2 +
– 2 + 
-  =
=  – 2 – 2
– 2 – 2
-  = -
= -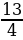
 =
= 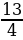
С= 6,5
у = 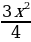 - 2х +
- 2х + 
у = 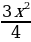 - 2х + 3,25 – частное решение
- 2х + 3,25 – частное решение
Ответ: у = 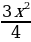 - 2х + 3,25
- 2х + 3,25
Пример 2. Решить дифференциальное уравнение 4х dх = 5у dу. Найти частное решение при х=0, у=1.
Решение:
4х dх = 5у dу

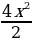 =
= 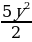 + С
+ С
2 х2 = 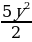 + С – общее решение
+ С – общее решение
Если х=0, у=1, то 2 . 02 =  + С
+ С
0 = 2,5 + С
С = - 2,5
2 х2 = 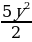 - 2,5 – частное решение
- 2,5 – частное решение
Ответ: 2 х2 = 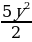 - 2,5.
- 2,5.
Задание:
| Вариант 1 | Вариант 2 |
Решить дифференциальное уравнение: 5xdx=2ydy. Найти частное решение при х=1, у=5.
Решить дифференциальное уравнение: 6dy=(2x – 1)dx. Найти частное решение при х=1, у=2.
| Решить дифференциальное уравнение: 2xdx=5ydy. Найти частное решение при х=1, у=5.
Решить дифференциальное уравнение: 4dy=(6x – 1)dx. Найти частное решение при х=1, у=2.
|
Практическая работа 13. Определение сходимости рядов
Цель работы: закрепление практических навыков определения сходимости числовых рядов.
Теоретический материал, методические рекомендации
Выражение  (1)
(1)
называется числовым рядом, числа  - членами ряда,
- членами ряда, 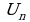 - общим членом ряда.
- общим членом ряда.
Сумма n первых членов ряда 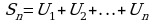 называется частичной суммой этого ряда.
называется частичной суммой этого ряда.
Ряд  называется сходящимся, если последовательность его частичных сумм имеет конечный предел:
называется сходящимся, если последовательность его частичных сумм имеет конечный предел: 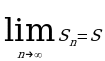 Значение S называется суммой ряда.
Значение S называется суммой ряда.
Если ряд не сходиться, то он называется расходящимся.
Признаки сходимости рядов
Необходимый признак сходимости ряда.
Если ряд (1) сходится, то 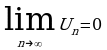 . (3)
. (3)
Этот признак сходимости является необходимым, но не достаточным.
Достаточный признак расходимости.
Если для ряда (1) предел  или не существует, то ряд расходится.
или не существует, то ряд расходится.
Признак Даламбера. Если для ряда (1)существует  (4)
(4)
то при D1 ряд расходится, при DD=1 вопрос остается нерешенным.
Признак Коши. Если для ряда (1) существует  (5)
(5)
то при C 1 ряд расходится, при C = 1 вопрос остается нерешенным.
Пример1 Исследовать на сходимость ряд 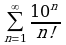 .
.
Решение:
Применим признак Даламбера; имеем 
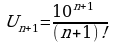 ,
,
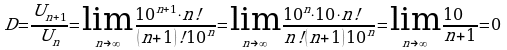
Так как D
Пример2. Исследовать на сходимость ряд 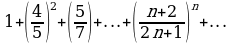
Решение:
Признак Коши для этого ряда дает:  .
.
Так как C
Алгоритм исследования на сходимость знакопеременных рядов
Исследовать на сходимость ряд, составленный из модулей членов данного ряда, используя
какой-либо признак сравнения.
Сделать вывод об абсолютной или условной сходимости этого ряда.
Выяснить, сходится ли данный знакочередующийся ряд, применяя признак Лейбница.
Для этого:
- Проверить, выполняется ли равенство для абсолютных величин членов ряда
- Найти предел общего члена ряда
- Сделать вывод о сходимости данного исходного ряда
Выполнить самостоятельно:
Вариант 1
Написать первые пять членов ряда по заданному общему члену, и проверить, выполняется ли необходимый признак сходимости ряда.


Установить расходимость ряда  с помощью достаточного признака расходимости ряда.
с помощью достаточного признака расходимости ряда.
Используя признак Даламбера, исследовать на сходимость ряд:
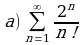
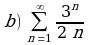
Используя признак Коши, исследовать на сходимость ряд:
а)  ; b)
; b) 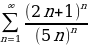
Вариант 2
Написать первые пять членов ряда по заданному общему члену, и проверить, выполняется ли необходимый признак сходимости ряда.
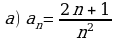
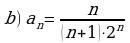
Установить расходимость ряда  с помощью достаточного признака расходимости ряда.
с помощью достаточного признака расходимости ряда.
Используя признак Даламбера, исследовать на сходимость ряд:
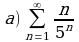

Используя признак Коши, исследовать на сходимость ряд:
а)  ; b)
; b) 
Практическая работа 14. Решение простейших вероятностных задач. Вычисление числовых характеристик случайной величины
Методические указания и теоретические сведения к практической работе
Классическое определение вероятности
Пример 1. Пусть в урне содержится 6 одинаковых шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Какова возможность вынуть наудачу из урны цветной шар? Можно ли охарактеризовать эту возможность числом? Оказывается можно. Это число и называется вероятностью события А (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.
Каждый из возможных результатов испытания (в примере 4, испытание состоит в извлечении шара из урны) называется элементарным исходом.
Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. В примере 4 благоприятствуют событию А (появление цветного шара) 5 исходов.
События называются равновозможными, если есть основания считать, что не одно из них не является более возможным, чем другое.
Пример 2. Появление того или иного числа очков на брошенном игральном кубике – равновозможные события.
Вероятностью P(A) события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность P(A) события А определяется по формуле
 ,
,
где m – число элементарных исходов, благоприятствующих A; n – число всех возможных элементарных исходов испытания.
В примере 4 всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того что взятый шар окажется цветным, равна P(A) = 5/6.
Пример 3. Определить вероятность выпадения нечётного числа очков на кости.
Решение. При бросании кости событие A – «выпало нечётное число очков» можно записать как подмножество {1, 3, 5} пространства исходов {1, 2, 3, 4, 5, 6} (рис. 1).

Рис. 1. Пространство исходов при бросании кости
Число всех равновозможных исходов n = 6, а число благоприятных событию A – m = 3. Следовательно,

Пример 4. В урне находится 7 шаров: 2 белых, 4 черных и 1 красный. Вынимается один шар наугад. Какова вероятность того, что вынутый шар будет чёрным?
Решение. Занумеруем шары. Пусть, например, шары с номерами 1 и 2 – белые, с номерами 3, 4, 5 и 6 – чёрные, а красному шару присвоим номер 7. Так как мы можем вынуть только один из семи шаров, то общее число равновозможных исходов равно семи (n = 7). Из них 4 исхода – появление шаров с номерами 3, 4, 5 и6 – приведут к тому, что вынутый шар будет чёрным (m = 4). Тем самым, вероятность события А, состоящего в появлении чёрного шара, равна 
Вычислите вероятность того, что вынутый шар будет белым.
Пример 5. Вычислить вероятность выпадения в сумме 10 очков при бросании пары костей.
Решение. Рассмотрим все равновозможные исходы в результате бросания двух костей (их число равно 36 - рекомендуем записать в виде таблицы). Выпадение в сумме 10 очков (событие А) возможно в трёх случаях – 4 очка на первой кости и 6 на второй, 5 очков на первой и 5 на второй, 6 очков на первой и 4 на второй. Поэтому вероятность события А (выпадения в сумме 10 очков) равна 
Пример 6. Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?
Решение.
1) Обозначим событие А - «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле: 
где m – число исходов, при которых появляется событие А,
n – общее число элементарных несовместных равновозможных исходов.
2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:

3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:

4) Определим вероятность события А:
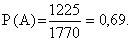
Ответ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены.
Свойство 1. Вероятность достоверного события А равна единице: Р(А) = 1.
Свойство 2. Вероятность невозможного события А равна нулю: Р(А) = 0.
Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей: 
Пример 7. Так как вероятность выпадения 13 очков при бросании пары костей – невозможное событие, его вероятность равна нулю.
Классическое определение вероятности предполагает, что число элементарных исходов испытания конечно. На практике же часто встречаются испытания, число возможных исходов которых бесконечно. Кроме этого, часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. По этой причине, наряду с классическим определением вероятности используют и другие определения, в частности статистическое определение.
Статистическое определение вероятности
Относительная частота наряду с вероятностью принадлежит к основным понятиям теории вероятностей.
Относительной частотой события А называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний:
 ,
,
где m – число появлений события А, n – общее число испытаний.
Классическая вероятность вычисляется до опыта, а относительная частота – после опыта.
Длительные наблюдения показали, что если в одинаковых условиях производят опыты, в каждом из которых число испытаний велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Это постоянное число и есть вероятность появления события.
Таким образом, при достаточно большом количестве испытаний в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней.
Пример 7. Естествоиспытатель К. Пирсон терпеливо подбрасывал монету и после каждого бросания не ленился записывать полученный результат. Проделав эту операцию 24 000 раз, он обнаружил, что герб выпадал в 12 012 случаях. Вычисляя относительную частоту выпадения герба, он получил ,
ч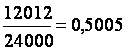 то практически равно 1/2.
то практически равно 1/2.
Задания практической работы
Вариант 1 – нечетные номера задач
Вариант 2 – четные номера задач
Задача 1. В урне находится 15 белых, 5 красных и 10 чёрных шаров. Наугад извлекается 1 шар, найти вероятность того, что он будет: а) белым, б) красным, в) чёрным.
Задача 2. В коробке лежат 8 зеленых, 7 синих и 15 красных карандашей. Вычислить вероятность того, что взятый наугад карандаш будет, синим или зеленым.
Задача 3. В одной коробке находится 4 белых и 8 черных шаров, а в другой – 3 белых и 9 черных. Из каждой коробки вынули по шару. Вычислить вероятность того, что оба шара окажутся белыми.
Задача 4. В магазин поступило 30 холодильников, пять из которых имеют заводской дефект. Случайным образом выбирают один холодильник. Какова вероятность того, что он будет без дефекта?
Задача 5. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наугад. Найти вероятность того, что набраны нужные цифры.
Задача 6. Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.
Задача 7. Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.
Задача 8. На шахматную доску случайным образом поставлены две ладьи. Какова вероятность, что они не будут бить одна другую?
Задача 9. Цифры 1, 2, 3, …, 9, выписанные на отдельные карточки складывают в ящик и тщательно перемешивают. Наугад вынимают одну карточку. Найти вероятность того, что число, написанное на этой карточке: а) четное; б) двузначное.
Задача 10. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: "а", "м", "р", "т", "ю". Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово "юрта".
Задача 11. Ребенок имеет на руках 5 кубиков с буквами: А, К, К, Л, У. Какова вероятность того, что ребенок соберет из кубиков слово "кукла"?
Задача 12. На полке в случайном порядке расставлено 40 книг, среди которых находится трехтомник Пушкина. Найти вероятность того, что эти тома стоят в порядке возрастания номера слева направо, но не обязательно рядом.
Задача 13. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему три вопроса?
Задача 14. На карточках написаны целые числа от 1 до 15 включительно. Наудачу извлекаются две карточки. Какова вероятность того, что сумма чисел, написанных на карточках, равна десяти?






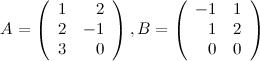

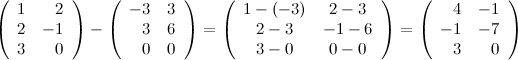


 .
. .
.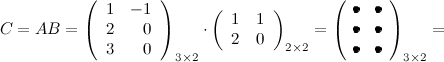

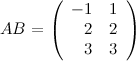 . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы
. В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы 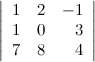 .
.
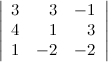
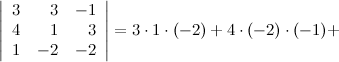
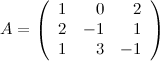
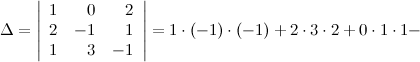
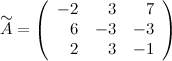



 2 8 5
2 8 5
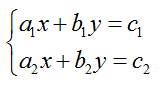 бычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
бычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой
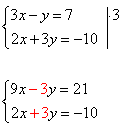
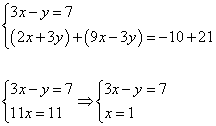
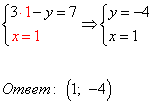
 Ответ: (1; -4).
Ответ: (1; -4). ) Если , то система (1) имеет единственное решение.
) Если , то система (1) имеет единственное решение.
 .
. ) Если , то система (1) имеет бесконечное множество решений.
) Если , то система (1) имеет бесконечное множество решений. .
. .
.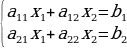
 ,
, 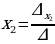 ,
, и
и 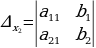 ,
,  .
. . Тогда система имеет единственное решение, определяемое формулами Крамера.
. Тогда система имеет единственное решение, определяемое формулами Крамера. . Если при этом хотя бы один из определителей
. Если при этом хотя бы один из определителей 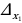 и
и 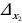 не равен нулю, то система не имеет решений.
не равен нулю, то система не имеет решений. и
и  , то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений.
, то одно из уравнений есть следствие другого, система сводится к одному уравнению с двумя неизвестными и имеет бесчисленное множество решений. .
. , и дополнительные определители
, и дополнительные определители 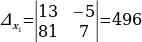 ,
, 
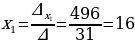 ,
, 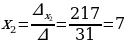
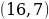 .
.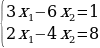 .
.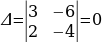 , и дополнительные определители
, и дополнительные определители  ,
,  . Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
. Коэффициенты уравнений системы пропорциональны, а свободные члены не подчинены той же пропорции. Система не имеет решений.
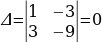 , и дополнительные определители
, и дополнительные определители 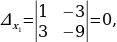
 .
.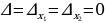 , то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на
, то одно уравнение есть следствие другого (второе уравнение получено из первого умножением на  ).
). , где числовые значения
, где числовые значения 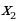 задаются произвольно и вычисляются соответствующие значения
задаются произвольно и вычисляются соответствующие значения  .
.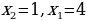 – частные.
– частные.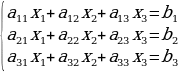
 . Система имеет единственное решение, определяемое формулами Крамера
. Система имеет единственное решение, определяемое формулами Крамера 
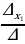 ,
,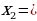
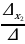 ,
,  , где
, где  и
и 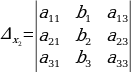 ,
, 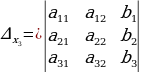 ,
,  .
. , не равен нулю, то система несовместна, решений не имеет.
, не равен нулю, то система несовместна, решений не имеет. , то система имеет бесчисленное множество решений.
, то система имеет бесчисленное множество решений.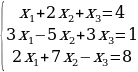
 и дополнительные определители
и дополнительные определители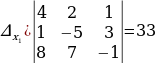
 ,
, 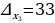 .
.
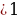 .
. .
.



 От третьей строки отнимаем вторую, умноженную на 3:
От третьей строки отнимаем вторую, умноженную на 3:  Умножив третью строку на 0,5 , получаем:
Умножив третью строку на 0,5 , получаем: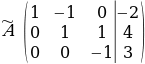
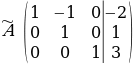


 Ответ.
Ответ. 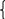 +у= -1
+у= -1

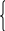 х-2у= -14
х-2у= -14
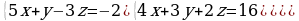
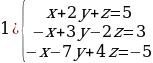
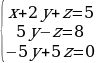

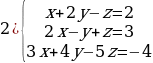
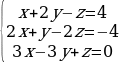

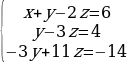
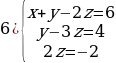

 =
= 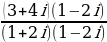 =
=  =
=  =
= =
= 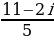 =
=  -
- 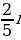



 2 0 x
2 0 x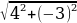 =
=
 лгебраическая форма комплексного числа -
лгебраическая форма комплексного числа - 

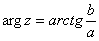 .
. i в тригонометрической и показательной формах.
i в тригонометрической и показательной формах.  -
-


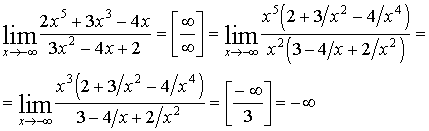

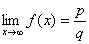 ,
,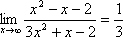
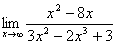



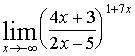
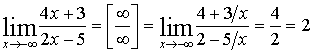
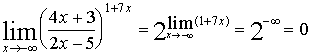
 ;
;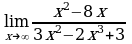 ;
; ;
; ;
; ;
;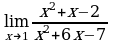

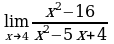
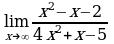

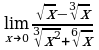




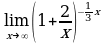
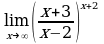



 ;
;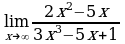 ;
;





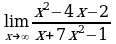
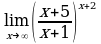



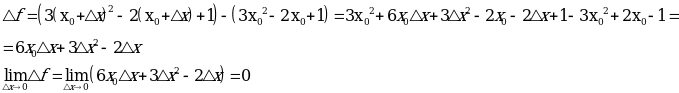
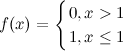 в точке
в точке  . Найдем односторонние пределы и значение функции в точке
. Найдем односторонние пределы и значение функции в точке 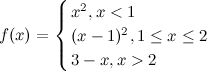 на непрерывность.
на непрерывность.
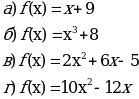
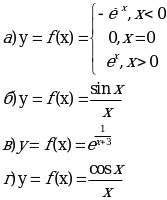

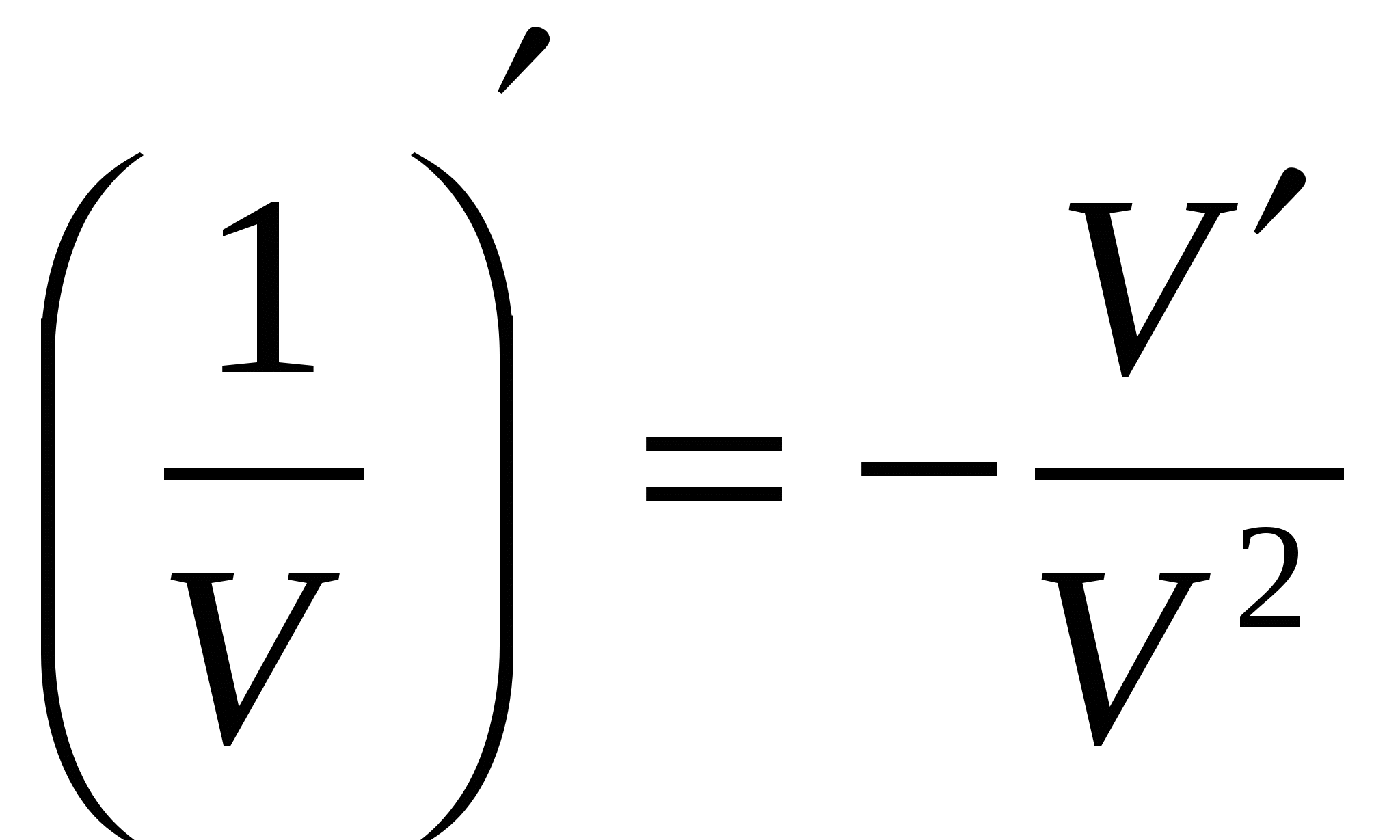 1)
1) 
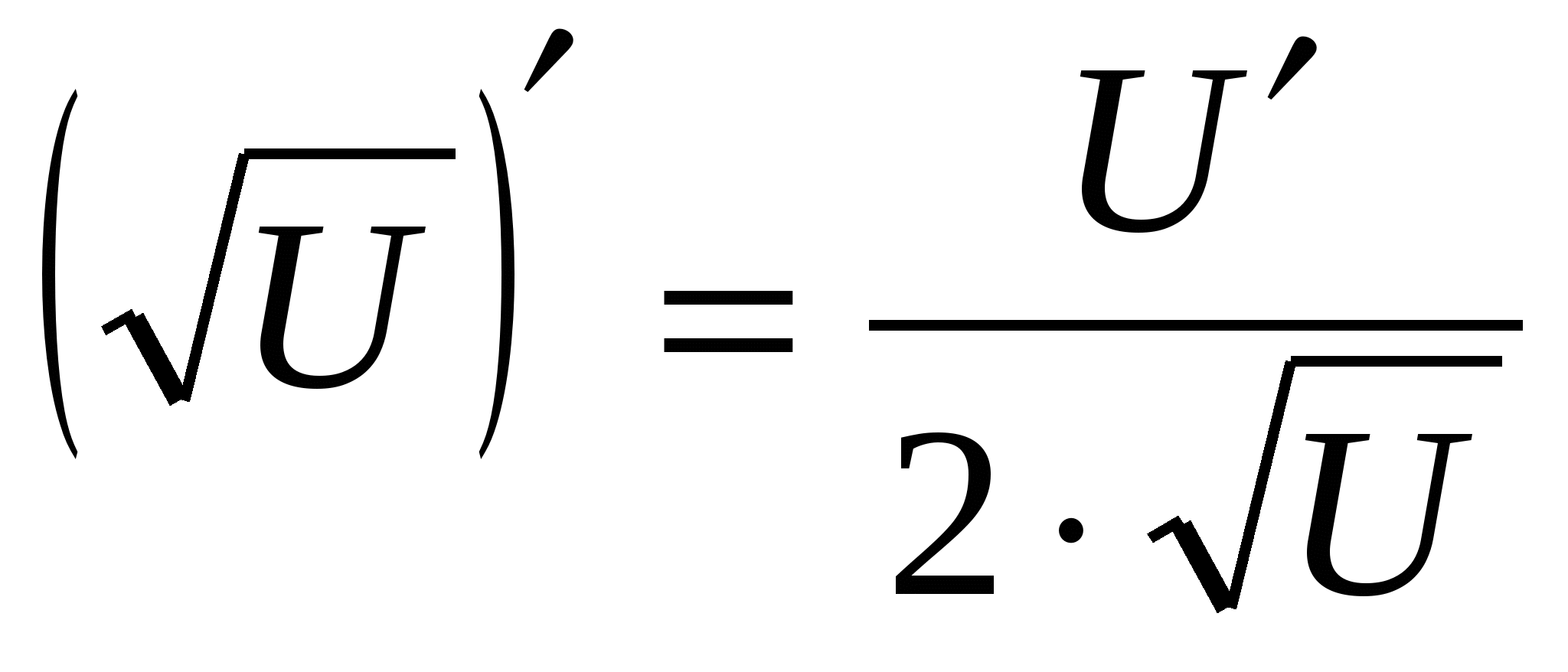 2)
2) 
 6
6 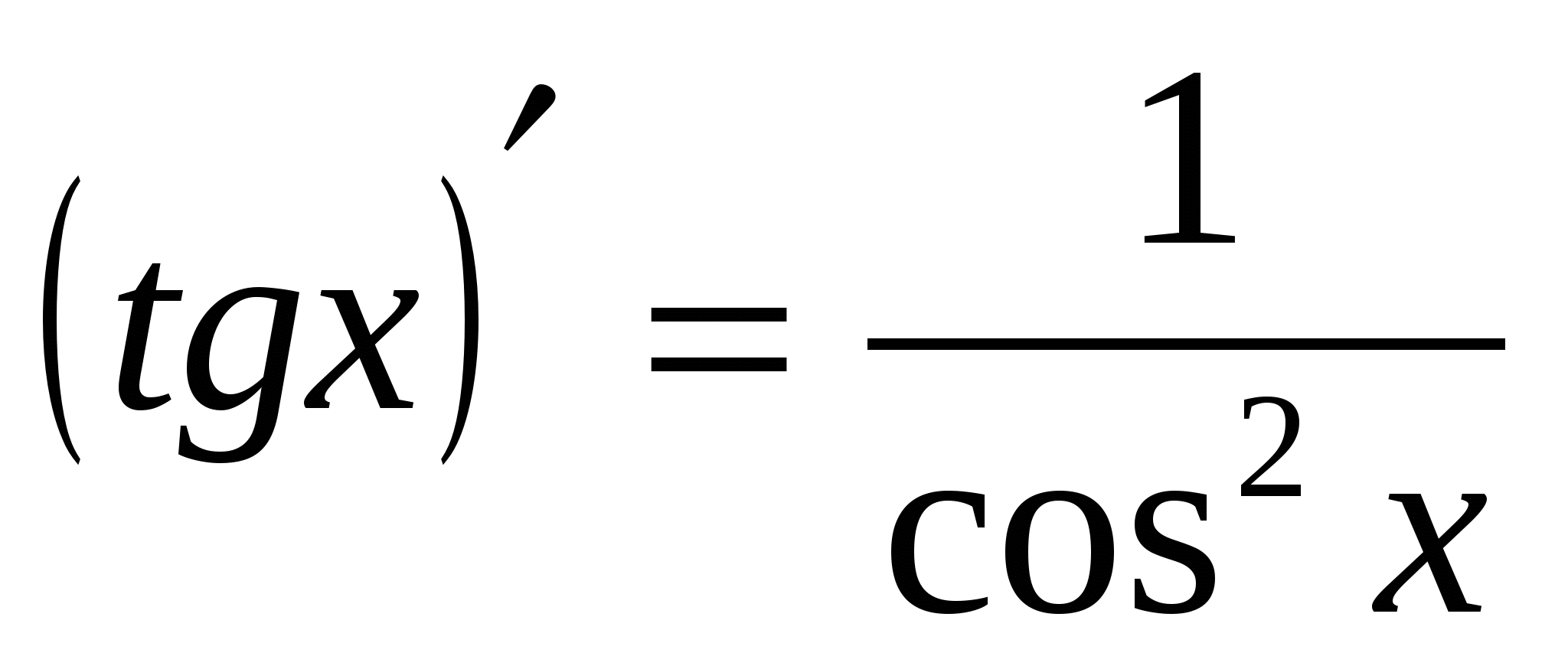
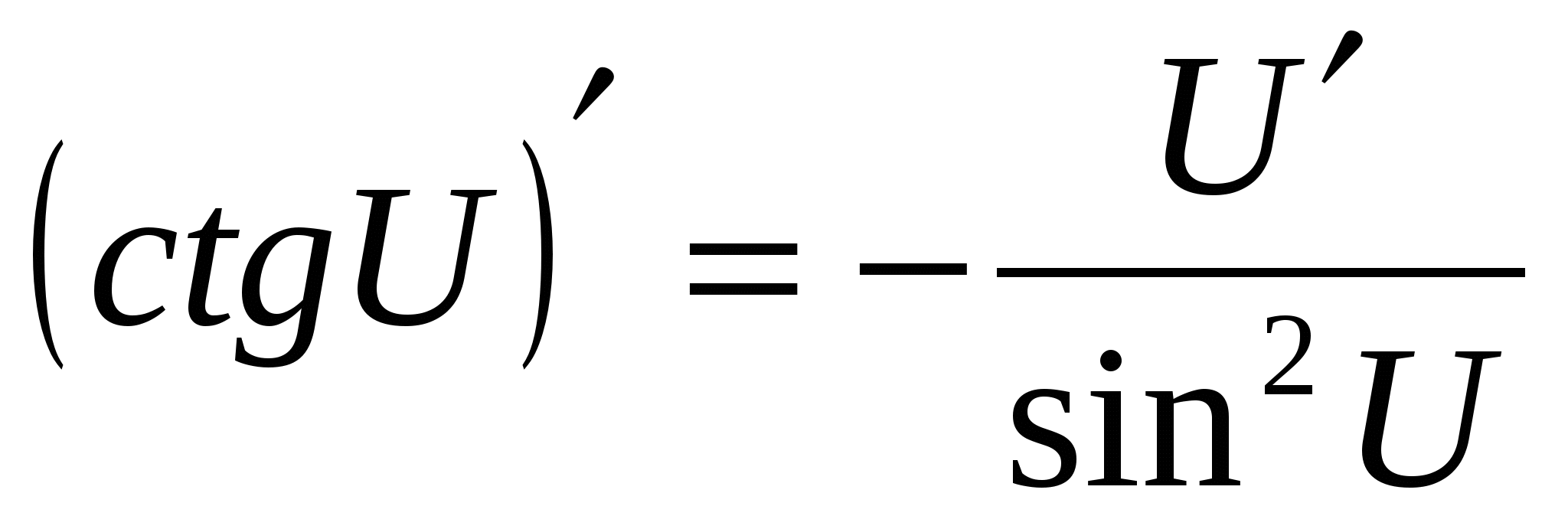 7
7 
 10
10 
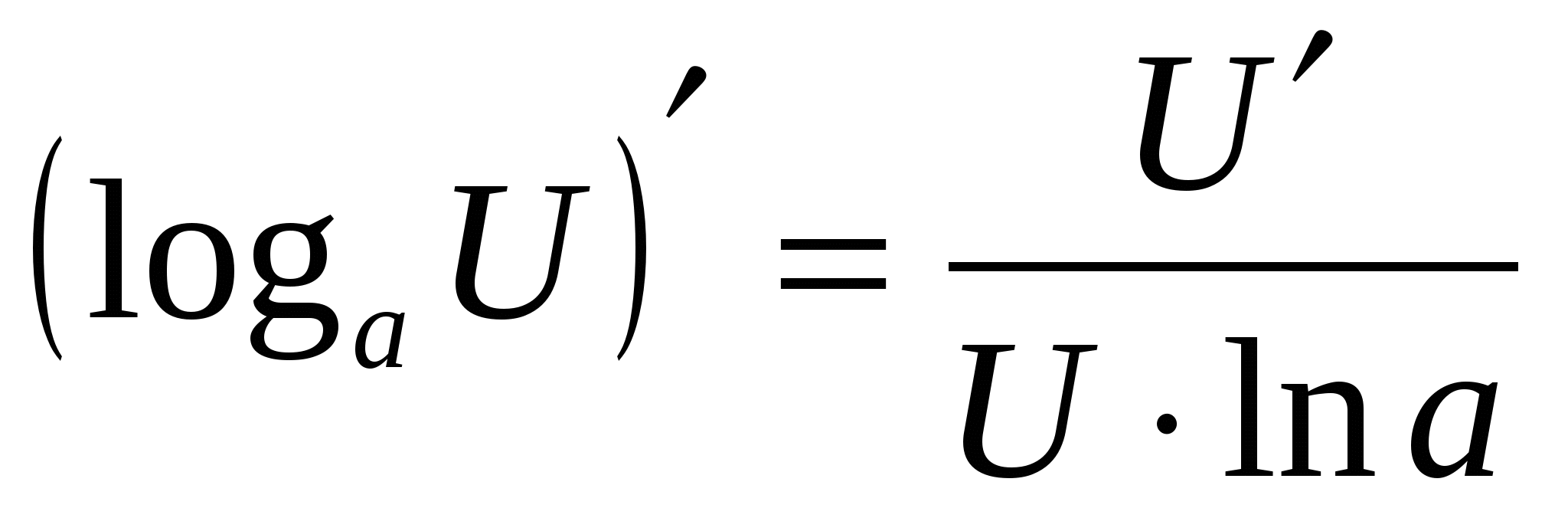 11
11
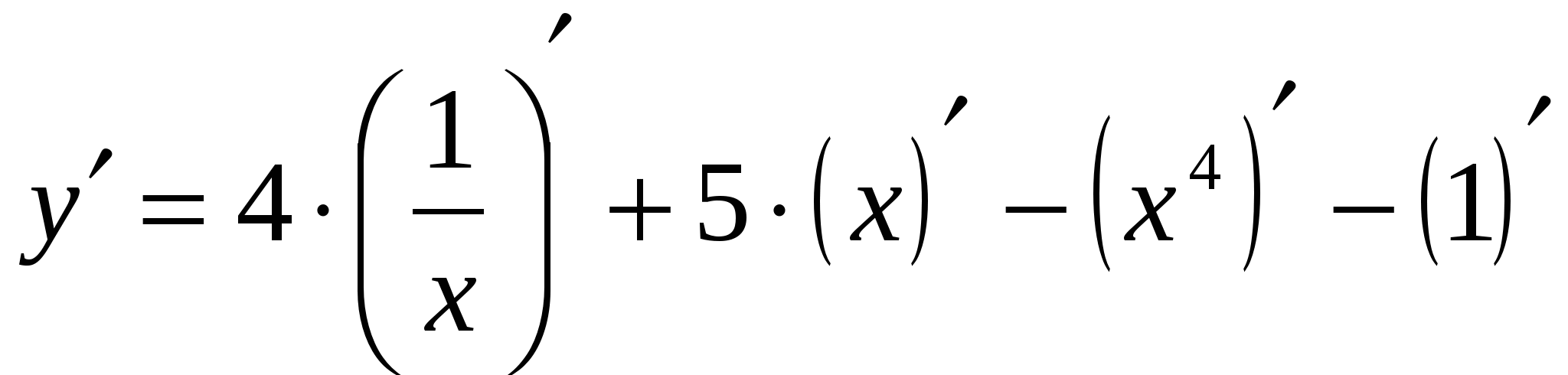
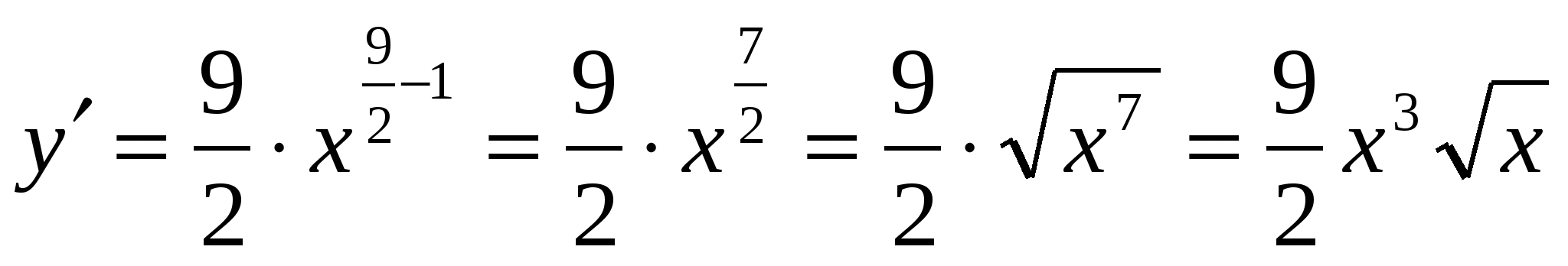 ( воспользовались формулой
( воспользовались формулой 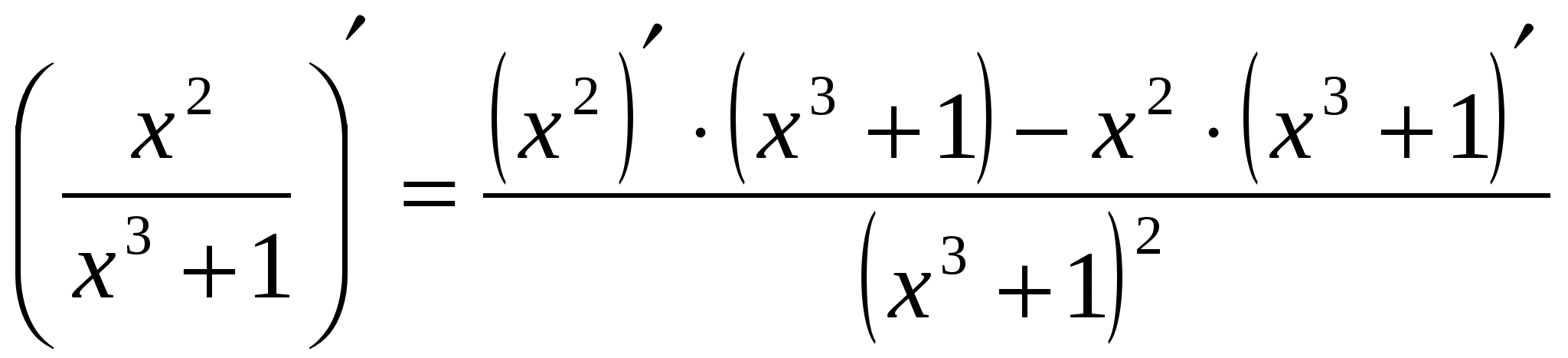

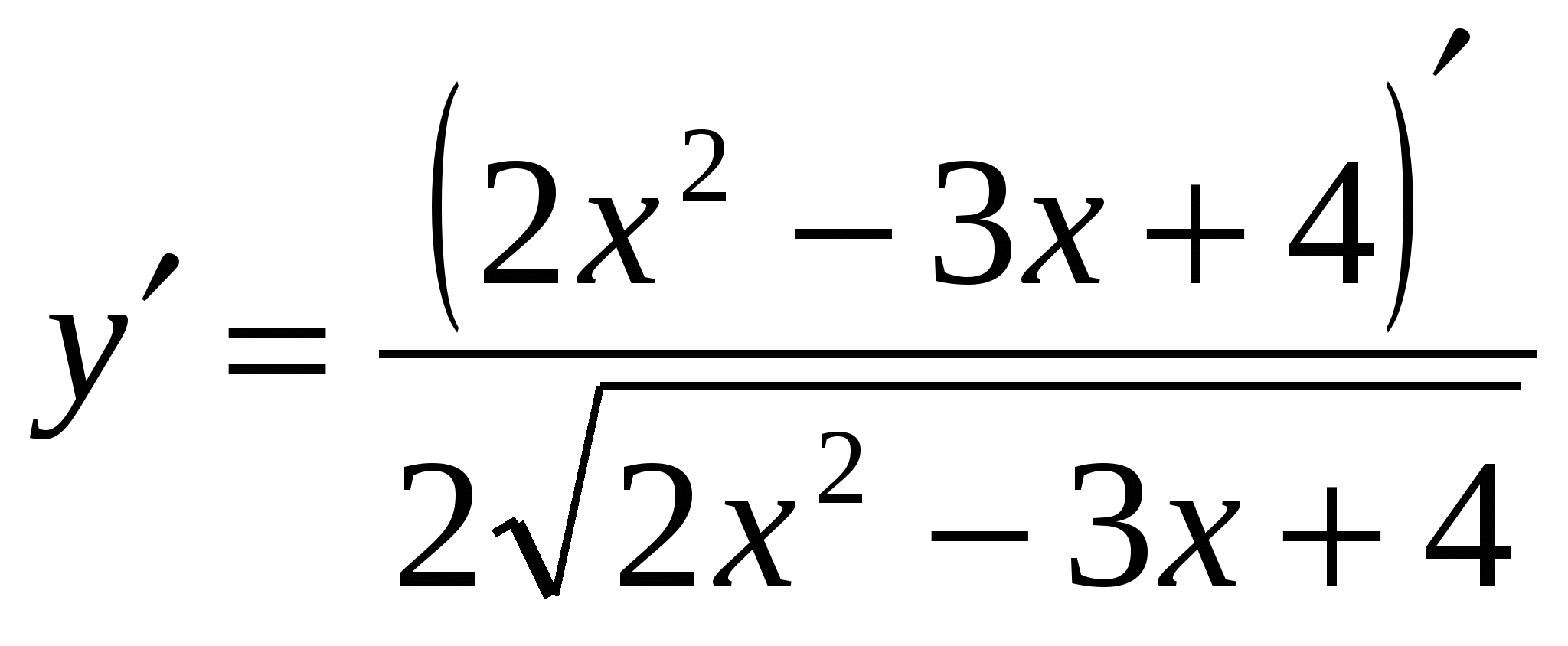 . Применим правила (2) и (4):
. Применим правила (2) и (4):  . По формуле (3) имеем:
. По формуле (3) имеем: 


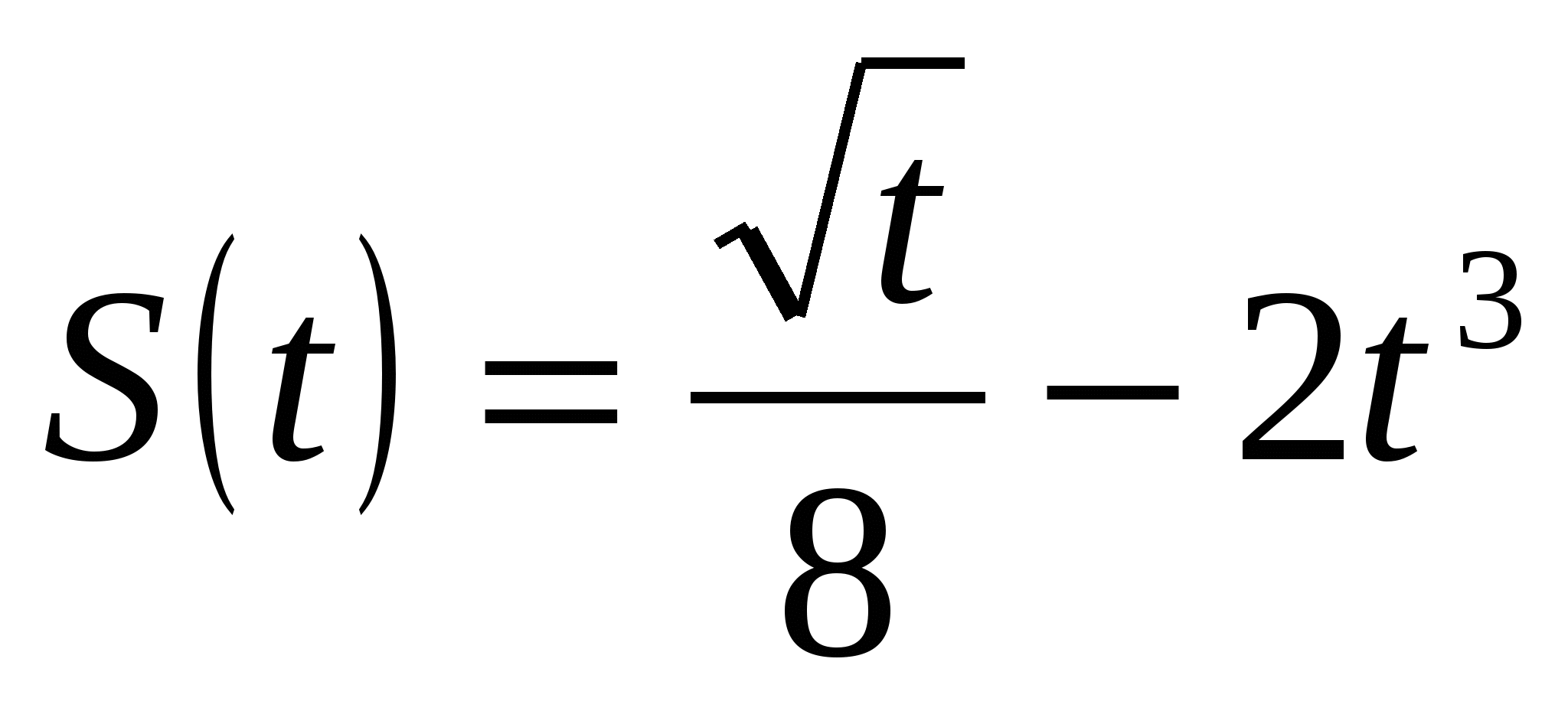
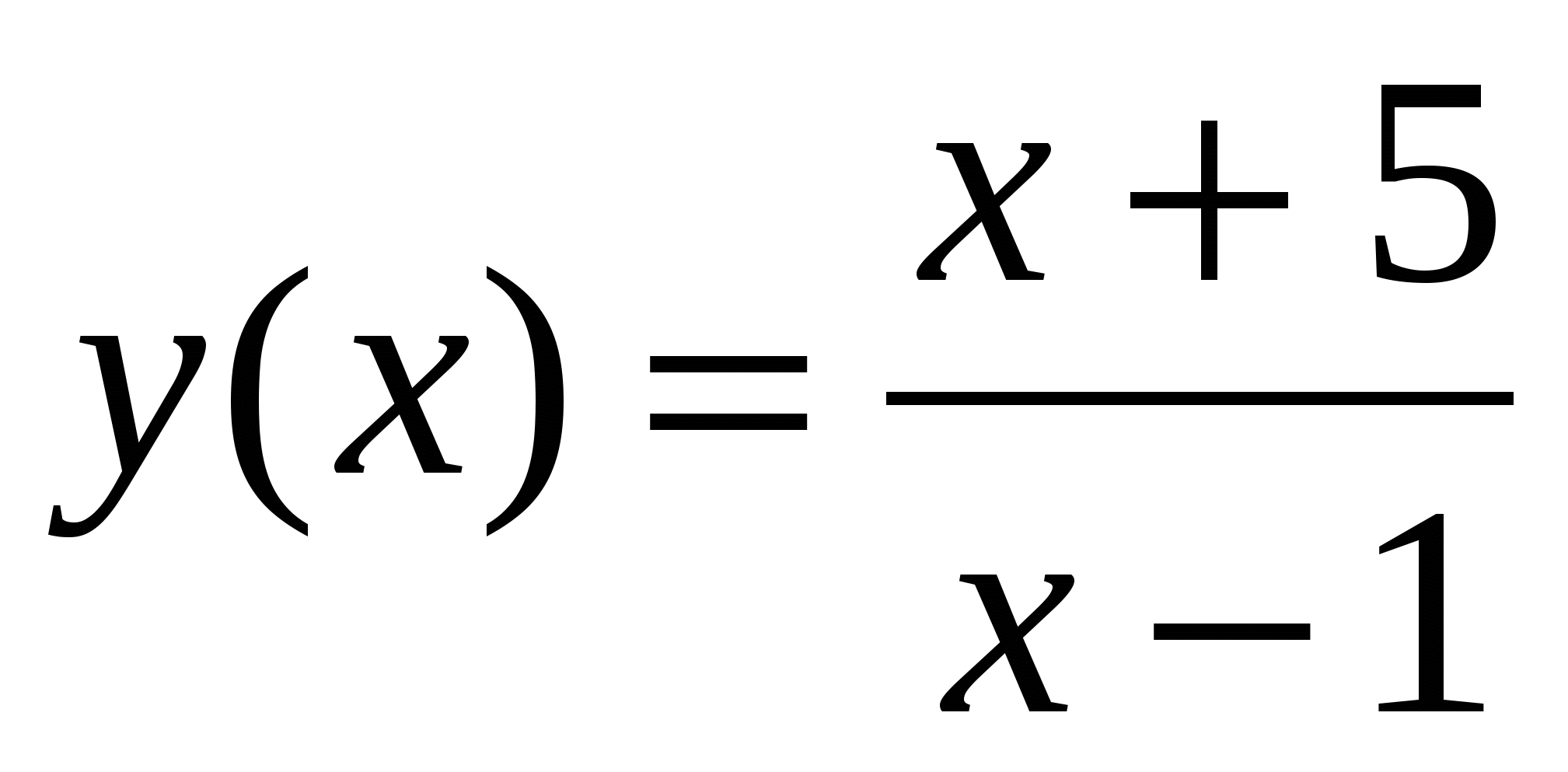


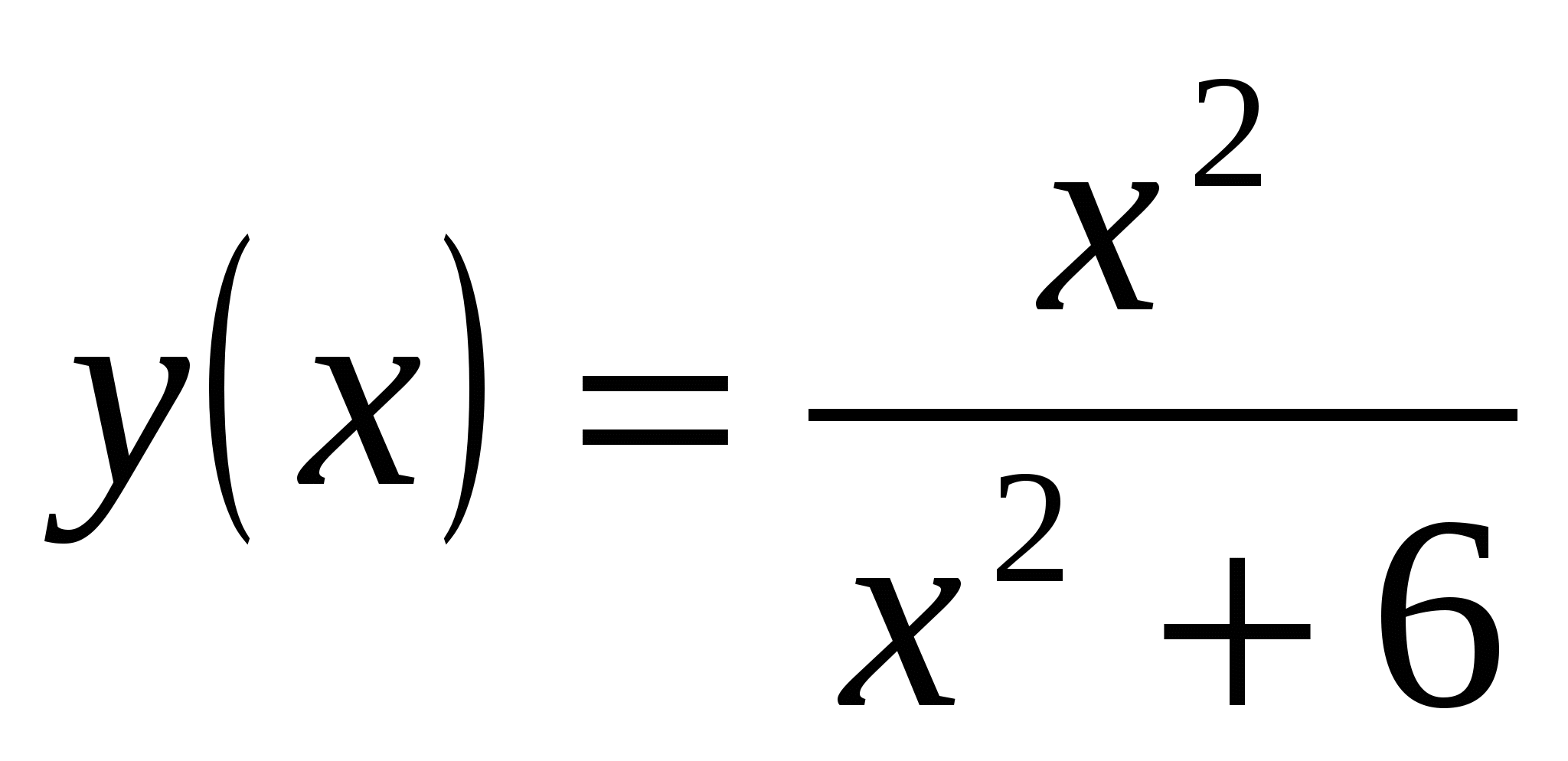
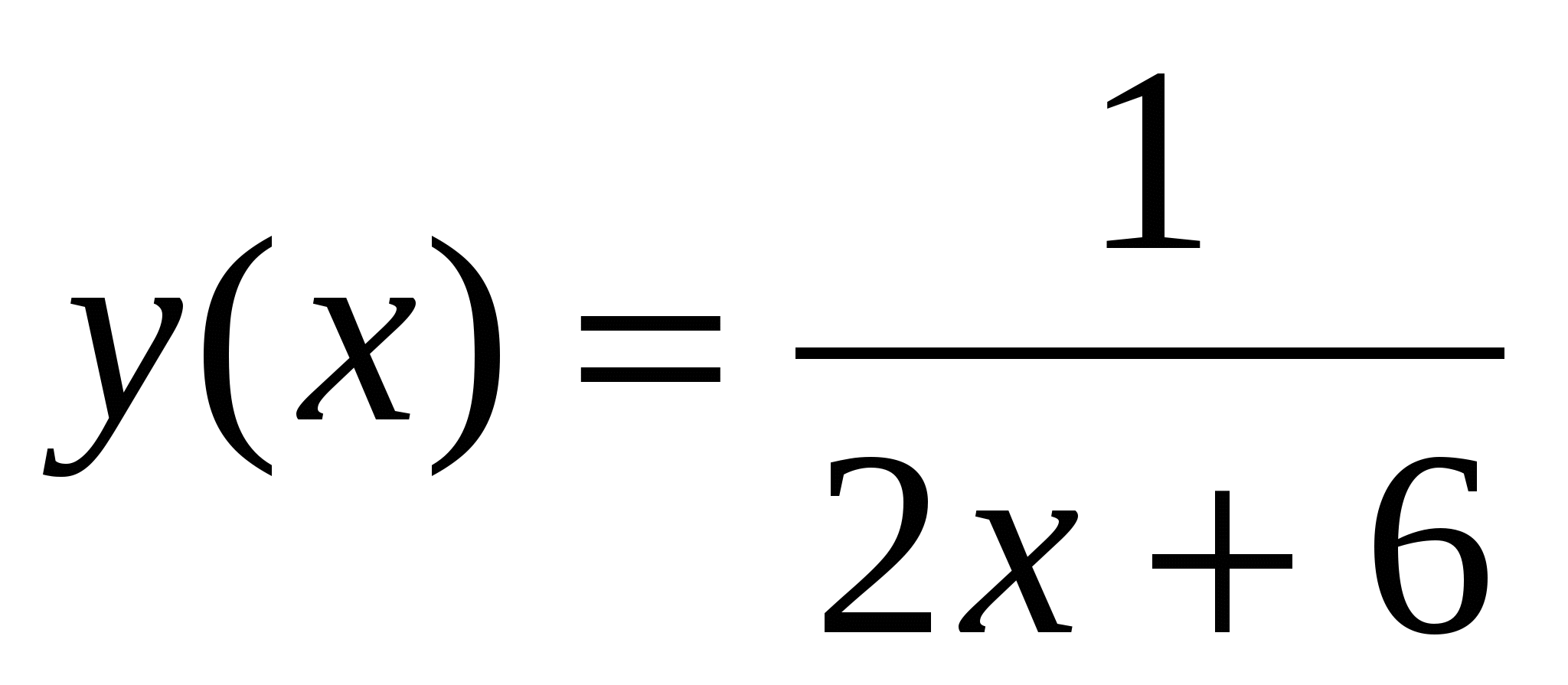


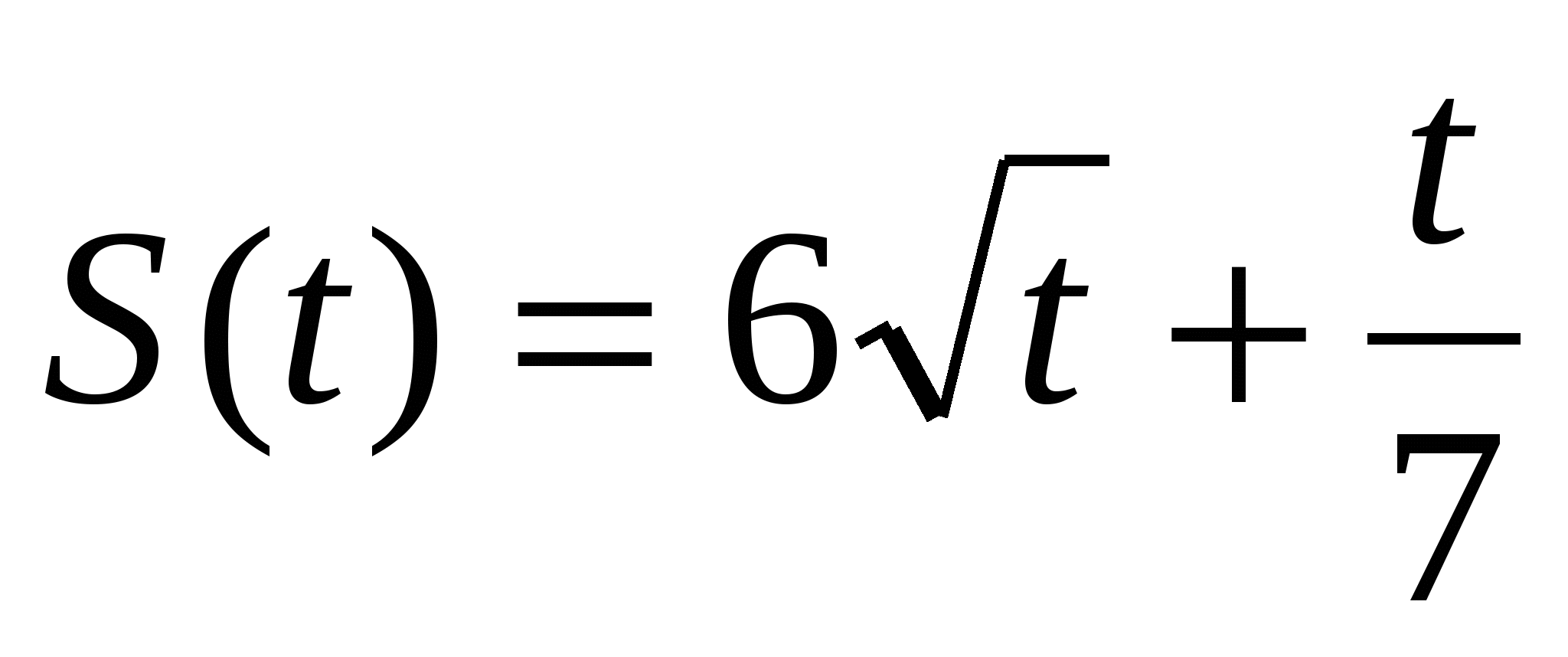

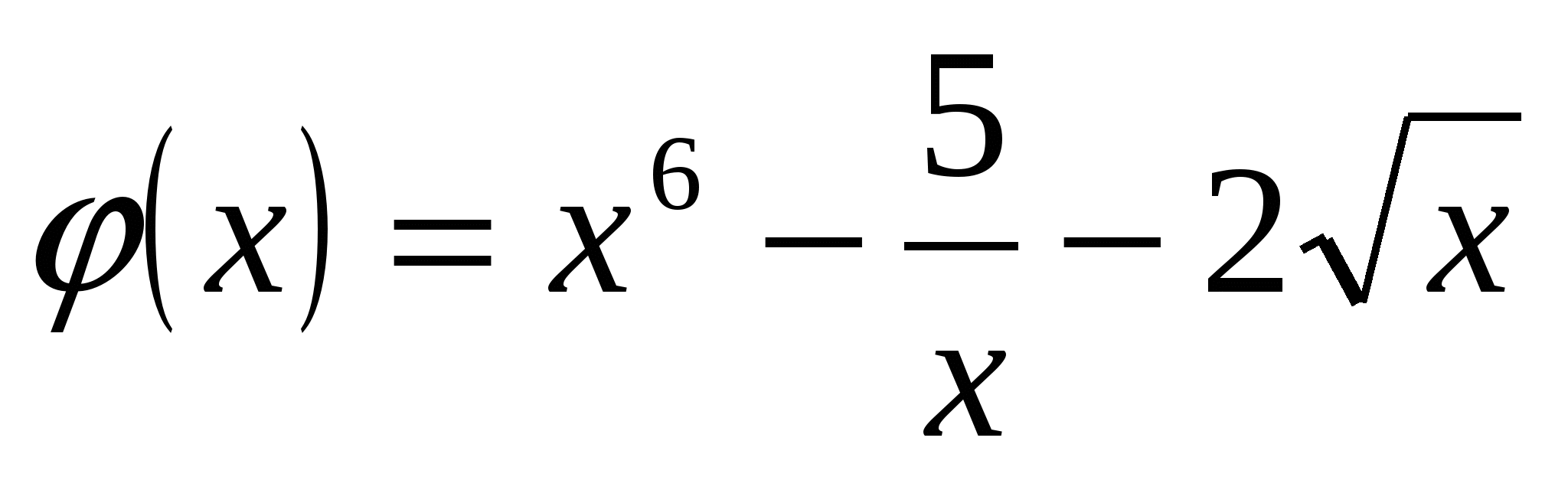




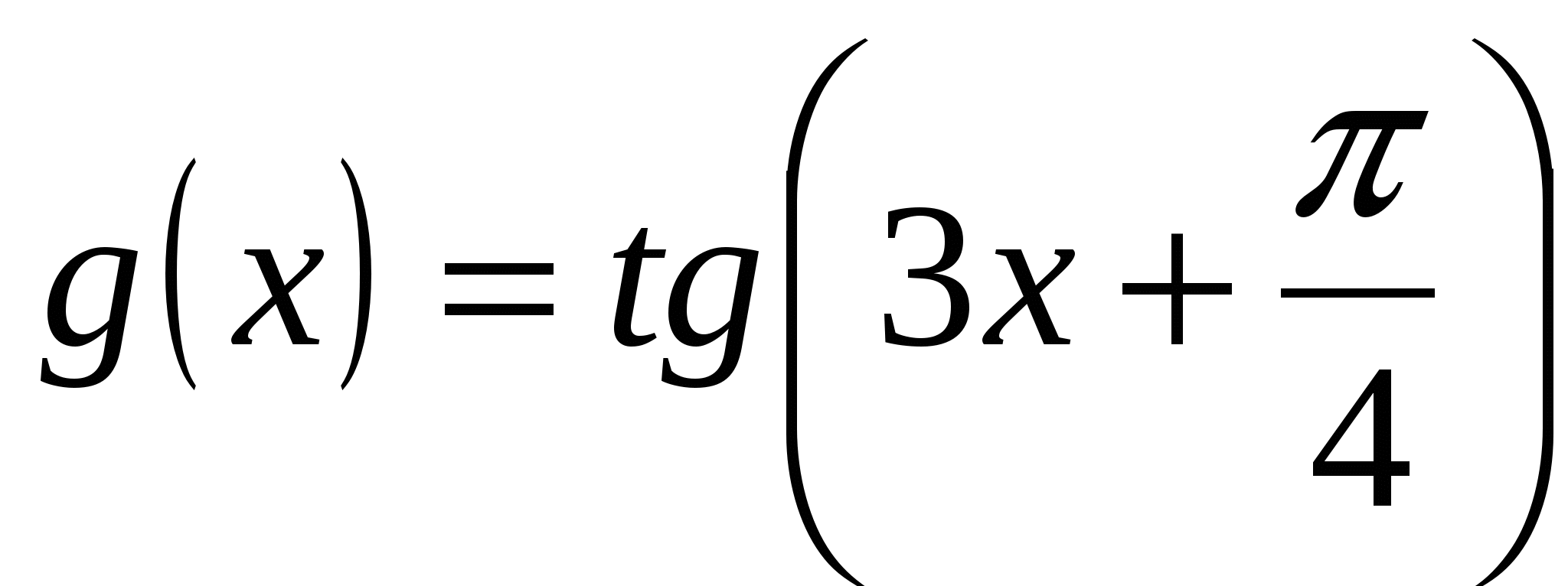

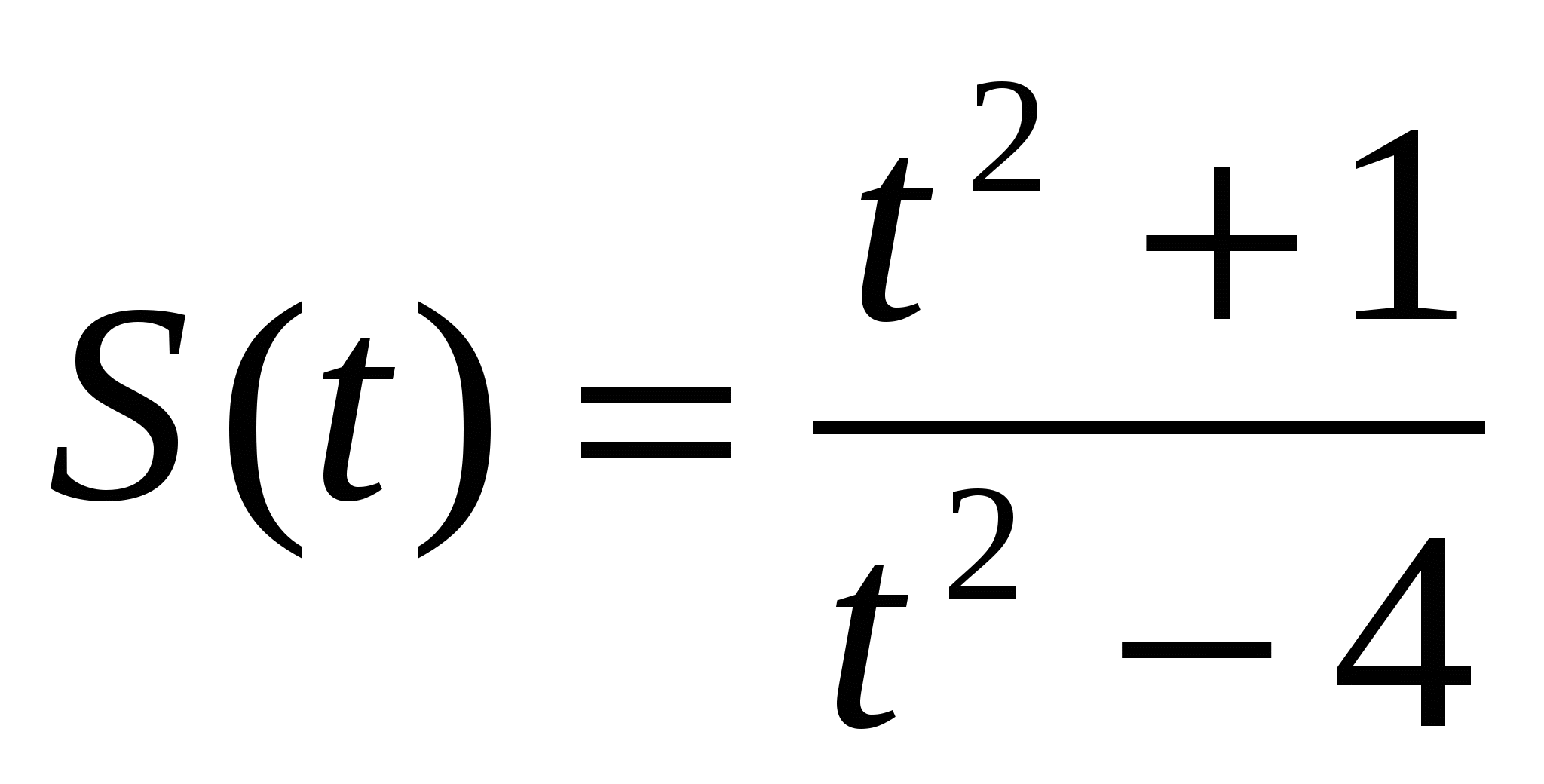
 .
. 
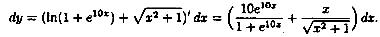



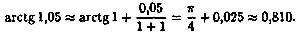
 ; г)
; г) 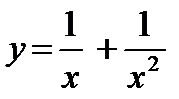 ; в)
; в) 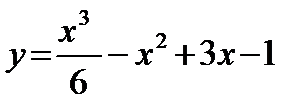 ; б)
; б)  ; б)
; б) 

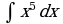


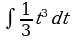

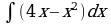







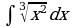
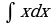


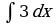
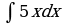

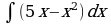
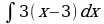
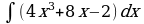


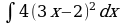


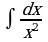
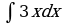



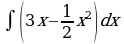
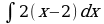


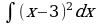
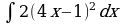


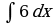

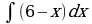
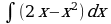
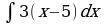
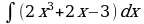
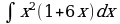
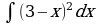
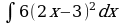



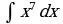



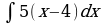

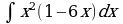

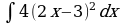

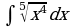




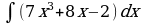




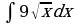

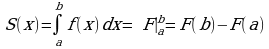
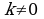 , то
, то 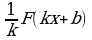 - первообразная для f(kx+b).
- первообразная для f(kx+b).
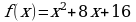 и прямой х = - 2.
и прямой х = - 2. , где а = 1, b = 8:
, где а = 1, b = 8:
 , где
, где

 =
= 
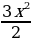 - 4х + С
- 4х + С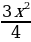 - 2х +
- 2х +  - общее решение
- общее решение – 2 . 1 +
– 2 . 1 +  – 2 +
– 2 + 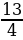


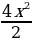 =
= 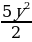 + С
+ С + С
+ С (1)
(1) - членами ряда,
- членами ряда, 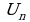 - общим членом ряда.
- общим членом ряда.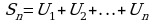 называется частичной суммой этого ряда.
называется частичной суммой этого ряда. называется сходящимся, если последовательность его частичных сумм имеет конечный предел:
называется сходящимся, если последовательность его частичных сумм имеет конечный предел: 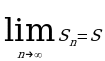 Значение S называется суммой ряда.
Значение S называется суммой ряда.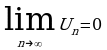 . (3)
. (3) или не существует, то ряд расходится.
или не существует, то ряд расходится. (4)
(4) (5)
(5)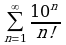 .
.
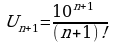 ,
,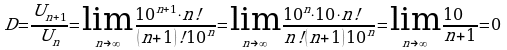
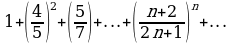
 .
.

 с помощью достаточного признака расходимости ряда.
с помощью достаточного признака расходимости ряда.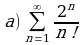
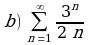
 ; b)
; b) 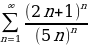
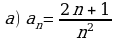
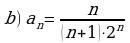
 с помощью достаточного признака расходимости ряда.
с помощью достаточного признака расходимости ряда.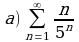

 ; b)
; b) 
 ,
,

 ,
,

















