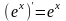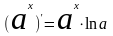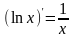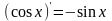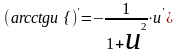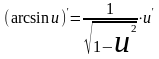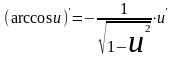Методические рекомендации по выполнению практических работ

Министерство образования Ставропольского края

Государственное бюджетное профессиональное образовательное учреждение

«Ставропольский региональный многопрофильный колледж»

Методические указания

по выполнению практических работ

по дисциплине ЕН 01 Математика

г. Ставрополь, 2020

Составитель: Кравченко Е.Б. преподаватель математики СРМК

Методические указания для выполнения практических работ являются частью основной профессиональной образовательной программы «Ставропольского регионального многопрофильного колледжа» по специальности 23.02.03 Техническое обслуживание и ремонт автомобильного транспорта в соответствии с требованиями ФГОС СПО третьего поколения.

Методические указания по выполнению практических работ адресованы студентам очной формы обучения.

Методические указания включают в себя учебную цель, перечень образовательных результатов, заявленных во ФГОС СПО третьего поколения, задачи, обеспеченность занятия, краткие теоретические и учебно-методические материалы по теме, вопросы для закрепления теоретического материала, задания для практической (лабораторной) работы студентов и инструкцию по ее выполнению, методику анализа полученных результатов, порядок и образец отчета о проделанной работе.

ЛИТЕРАТУРА

Основные источники:

1. Матвеева, Т. А. Математика : учебное пособие для СПО / Т. А. Матвеева, Н. Г. Рыжкова, Л. В. Шевелева ; под ред. Д. В. Александрова. — 2-е изд. — Саратов, Екатеринбург : Профобразование, Уральский федеральный университет, 2019. — 215 c. — ISBN 978-5-4488-0397-0, 978-5-7996-2868-0. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/87821.html

(дата обращения: 01.10.2019). — Режим доступа: для авторизир. пользователей

Дополнительные источники:

1. Алпатов, А. В. Математика: учебное пособие для СПО / А. В. Алпатов. — Электрон.текстовые данные. — Саратов : Профобразование, 2019. — 96 c. — ISBN 978-5-4488-0150-1. — URL: http://www.iprbookshop.ru/65731.html (дата обращения: 19.06.2019).-

2. Богун, В. В. Проектная деятельность по математике. Математический анализ : учебное пособие для СПО / В. В. Богун. — Саратов : Профобразование, Ай Пи Ар Медиа, 2020. — 144 c. — ISBN 978-5-4488-0739-8, 978-5-4497-0430-6. — Текст : электронный // Электронно-библиотечная система IPR BOOKS : [сайт]. — URL: http://www.iprbookshop.ru/92639.html (дата обращения: 06.05.2020). — Режим доступа: для авторизир. Пользователей

3. Григорьев, В.П. Математика: учебник для студ. учреждений сред.проф. образования / В.П. Григорьев, Т.Н. Сабурова.– М.: Академия, 2017.-368 с.-2500 экз.- ISBN 978-5-4468-5334-2.- ( Топ 50. Профессиональное образование).-Текст: непосредственный

4. Башмаков, М.И. Математика: алгебра и начала математического анализа, геометрия: учебник / М.И. Башмаков. – 3-е изд., стер. – М.: Академия, 2017.-256 с.-8000 экз.- ISBN 978-5-4468-4416-6.-Текст: непосредственный.

5. Григорьев, В.П. Математика: учебник для студ. учреждений сред.проф. образования / В.П. Григорьев, Т.Н. Сабурова.– М.: Академия, 2016.-368 с.-2500 экз.- ISBN 978-5-4468-1490-9.- Текст: непосредственный.

6. Башмаков, М.И. Математика: алгебра и начала математического анализа, геометрия: задачник: учеб. Пособ. Для студ. Учреждений сред.проф. образования / М.И. Башмаков. – 4-е изд., стер. – М.: Академия, 2017.-416 с.-3000 экз.-ISBN 978-5-4468-5127-0.-Текст: непосредственный.

Интернет-ресурсы:

1. Задачи и упражнения по математическому анализу и дифференциальным уравнениям [Электронный ресурс] : учебное пособие / В. В. Власов, С. И. Митрохин, А. В. Прошкина [и др.]. — Электрон. текстовые данные. — Москва, Саратов : Интернет-Университет Информационных Технологий (ИНТУИТ), Вузовское образование, 2017. — 376 c. — 978-5-4487-0077-4. — Режим доступа: http://www.iprbookshop.ru/67393.html

2. Берникова, И. К. Математика для гуманитариев [Электронный ресурс] : учебно-методическое пособие / И. К. Берникова, И. А. Круглова. — Электрон. текстовые данные. — Омск : Омский государственный университет им. Ф.М. Достоевского, 2016. — 200 c. — 978-5-7779-1991-5. — Режим доступа: http://www.iprbookshop.ru/59612..html

3. Краткий курс высшей математики [Электронный ресурс] : учебник / К. В. Балдин, Ф. К. Балдин, В. И. Джеффаль [и др.] ; под ред. К. В. Балдин. — Электрон. текстовые данные. — М. : Дашков и К, 2015. — 512 c. — 978-5-394-02103-9. — Режим доступа: http://www.iprbookshop.ru/52265.html

4. Алпатов, А. В. Математика [Электронный ресурс] : учебное пособие для СПО / А. В. Алпатов. — 2-е изд. — Электрон. текстовые данные. — Саратов : Профобразование, Ай Пи Эр Медиа, 2019. — 162 c. — 978-5-4486-0403-4, 978-5-4488-0215-7. — Режим доступа: http://www.iprbookshop.ru/80328.html

5. Математика. Элементы высшей математики: учебник: в 2 т. Т. 1 / В.В. Бардушкин, А.А. Прокофьев. — М.: КУРС, НИЦ ИНФРА-М, 2019. — 304 с. — (Среднее профессиональное образование). - Режим доступа: http://znanium.com/catalog/product/978660

6.Математика управления капиталом: Методы анализа риска для трейдеров и портфельных менеджеров / Винс Р., - 4-е изд. - М.:Альпина Пабл., 2016. - 400 с.: ISBN 978-5-9614-1529-2 - Режим доступа: http://znanium.com/catalog/product/914276

СОДЕРЖАНИЕ

Название практических работ	страницы
Нахождение производных	7
Дифференцирование сложных функций	9
Исследование функции методами дифференциального исчисления	11
Нахождение неопределенного интеграла	14
Интегрирование функций	16
Вычисление определенного интеграла.	19
Дифференциальные уравнения первого порядка	22
Частные решения дифференциальных уравнений	24
Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами	25
Решение задач с применением теории множеств	27
Решение задач с применением теории графов	30
Решение практических задач с применением вероятностных методов	34

Введение

УВАЖАЕМЫЙ СТУДЕНТ!

Методические указания по дисциплине ЕН. 01 Математика для выполнения практических работ созданы Вам в помощь для работы на занятиях, подготовки к практическим работам, правильного составления отчетов.

Приступая к выполнению практической работы, Вы должны внимательно прочитать цель и задачи занятия, ознакомиться с требованиями к уровню Вашей подготовки в соответствии с федеральными государственными стандартами третьего поколения (ФГОС-3), краткими теоретическими и учебно-методическими материалами по теме практической работы, ответить на вопросы для закрепления теоретического материала.

Все задания к практической работе Вы должны выполнять в соответствии с инструкцией, анализировать полученные в ходе занятия результаты по приведенной методике.

Отчет о практической работе Вы должны выполнить по приведенному алгоритму, опираясь на образец.

Наличие положительной оценки по практическим работам необходимо для получения дифференцированного зачета по дисциплине, поэтому в случае отсутствия на уроке по любой причине или получения неудовлетворительной оценки за практическую Вы должны найти время для ее выполнения или пересдачи.

Внимание! Если в процессе подготовки к практическим работам или при решении задач у Вас возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий.

Время проведения дополнительных занятий можно узнать у преподавателя или посмотреть на двери его кабинета.

Желаем Вам успехов!!!

Раздел 1. Основные понятия и методы математического анализа.

Тема 1.1 Основы дифференциального исчисления

Практическая работа №1 Нахождение производных

Учебная цель: уметь находить производные элементарных функций, производные произведения и частного.

Учебные задачи:

1) провести устный опрос по теоретическим вопросам

2) провести письменный опрос по формулам и правилам дифференцирования

3) выполнить задания на дифференцирование функций

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить производные элементарных функций

- - находить производные произведения и частного

знать:

- определение производной

- геометрический смысл производной

- формулы и правила дифференцирования

Задачи практической работы

1. Повторение теоретического материала

2. Проверка знаний формул и правил дифференцирования

3. Выполнение заданий на дифференцирование функций.

Содержание работы:

Формулы дифференцирования
1. (xn)'=nxn-1 2. 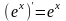3. 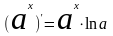4. 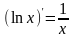5. 6. 7. 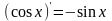8. 9. 10. 11. 12.	13. (xu)'=uxu-1·u' 14. 15. 16. 17. 18. 19. 20. 21. 22. 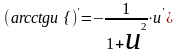23. 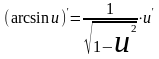24. .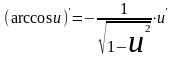
Правила дифференцирования
1. 2. 3. 4. 5.

Примеры вычислений :

1) f(x)=3x⁴+2x²-5x+3; используя формулы (xⁿ)'=nx^n-1 , x'=1 , с'=0

и правила (cu)'=cu' , получаем

f'(x)=(3x⁴+2x²-5x+3)')=(3x⁴)'+(2x²)'-(5x)'+(3)'=3(x⁴)'+2(x²)'-5(x)'+(3)'=3·4х³+2·2х¹-5·1+0=12х³+4х-5

2) f(x)=x³cosx ; используя формулы (xⁿ)'=nx^n-1 и (cosx)'=-sinx и правило

получаем

f'(x)=(x³cosx)'= (x³)'cosx+ x³ (cosx)'=3х²соsx+x³(-sinx) =3х²соsx-x³sinx

3) f(x)=x⁴ /cosx ; используя формулы (xⁿ)'=nx^n-1 и (cosx)'=-sinx и правило

получаем

f'(x)=(x⁴ /cosx)'= ((x⁴)'cosx- x⁴ (cosx)')/cos²x=(4х³соsx-x⁴(-sinx))/ cos²x =(4х³соsx+x⁴sinx)/ cos²x

Вариант 1.	Вариант 2.
Найдите производную 1. f(x)=3x8+6x3-7x+1; 2. f(x)=5x3sinx; 3. f(x)=6x2lnx 4. f’ (х) = ; 5. f(x) = sinx-5cosx +28x; 6. f(x) = -6	Найдите производную 1. f(x)=2x6-9x2+5x-8; 2. f(x)=6x4cosx; 3. f(x)=2x3lnx 4. f’ (х) = ; 5. f(x) = sinx-8cosx +7x; 6. f(x) = +3.14

Тема 1.1 Основы дифференциального исчисления

Практическая работа №2 Дифференцирование сложных функций

Учебная цель: уметь находить производные сложных функций.

Учебные задачи:

1) провести устный опрос по теоретическим вопросам

2) провести письменный опрос по формулам и правилам дифференцирования

3) выполнить задания на дифференцирование функций

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить производные элементарных функций

- находить производные сложных функций

- находить производные произведения и частного

знать:

- определение производной

- геометрический смысл производной

- формулы и правила дифференцирования

Задачи практической работы

1. Повторение теоретического материала

2. Проверка знаний формул и правил дифференцирования

3. Выполнение заданий на дифференцирование функций.

Содержание работы:

Формулы дифференцирования
1. (xn)'=nxn-1 2. 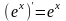3. 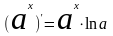4. 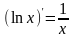5. 6. 7. 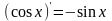8. 9. 10. 11. 12.	13. (xu)'=uxu-1·u' 14. 15. 16. 17. 18. 19. 20. 21. 22. 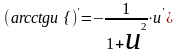23. 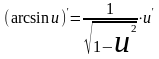24. .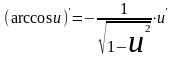
Правила дифференцирования
1. 2. 3. 4. 5.

Примеры вычислений :

1) f(x)=cos(3x²+2) ; используя формулы ,

а потом (xⁿ)'=nx^n-1 , x'=1 , с'=0

получаем f'(x) =cos'(3x²+2)· (3x²+2)'= -sin(3x²+2)·6x=-6х·sin(3x²+2)

2) f(x)=e ^7x+8; используя формулы ( , а потом (xⁿ)'=nx^n-1 , x'=1 , с'=0

получаем f'(x) = (e ^7x+8)'= e ^7x+8·(7х+8)'= e ^7x+8·7=7e ^7x+8·

Вариант 1.	Вариант 2.
Найдите производную 1. f(x) = sin(2x2 – 3x + 1); 2 . f(x) = cos3(2x – 1); 3 . f(x)=6 4x+1 4 . f(x)=(5x+7)3 5 .f(x)=log 24x 6 . f(x)=ln3x	Найдите производную 1 . f(x) = cos(3x2 – 4x + 2); 2 . f(x) = sin3(2 - 3x) 3 . f(x)=6 4x+1 4 . f(x)=(5x+7)3 5 .f(x)=log 24x 6. f(x)=ln3x

Тема 1.1 Применение производной к исследованию функции.

Практическая работа №3. Исследование функции методами

дифференциального исчисления

Учебная цель: используя схему исследования функции и производную уметь строить графики функций.

Учебные задачи:

1) провести математический диктант по материалу лекций

2) совместно разобрать пример исследования функции с помощью производной

3) выполнить задания на самостоятельное исследование функции

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить производные элементарных функций

- находить промежутки возрастания и убывания функции, экстремумы функции

- находить точки перегиба функции

- проводить исследование функции по схеме и строить ее график

знать:

- схему исследования функции

- достаточные признаки возрастания и убывания функции

- необходимый и достаточный признаки экстремума функции

- достаточный признак точки перегиба функции

Задачи практической работы

1.Повторение теоретического материала

2. Объяснение задания на исследование функции

3. Самостоятельное выполнение заданий на исследование функции.

Содержание работы:

Общая схема исследования функции и построение её графика.

1. Найдите область определения функции.

2. Исследуйте функцию на четность или нечетность.

3.Найдите точки пересечения графика функции с осями координат

4. Найдите промежутки монотонности функции, её экстремумы.

5. Найдите промежутки выпуклости графика функции, её точки

перегиба.

6. Постройте график функции, используя полученные результаты

исследования.

Пример исследования

Построить график функции: f(x)= x³+x²-5x+3

Исследование

1. D(y) = R

2. Исследование на четность

f(-x)=(- x)³+(-x)²-5(-x)+3= -x³+x²+5x+3≠ f(x)-четной не является

f(-x)=-( x³-x²-5x-3) ≠ -f(x)-нечетной не является

Вывод: функция ни четная, ни нечетная; график не симметричен

1. Точки пересечения графика функции с осями координат

С осью ОУ: х=0, у= 0³+0²-5·0+3=3 А(0;3)

С осью ОХ: у=0, x³+x²-5x+3=0- уравнение имеет корни, но его решение представляет трудность.

4. Найдите промежутки монотонности функции, её экстремумы.

Найдем производную: f'(x)= (x³+x²-5x+3)' =3x²+2x-5

Найдем критические точки f'(x)=0, 3x²+2x-5=0

D=b²-4aс, D=2²-4·3·(-5)=4+60=64=8²

х_1,2=(-b±√D)/2a

x₁=(-2+8)/2·3=1, x₂=(-2-8)/2·3=-5/3-критические точки

Н анесем критические точки на числовую ось

+

-

+

-5/3

1

Так как старший коэффициент у производной положительный (при х² 3x²+2x-5 равен 3, а 3 больше нуля), то знаки на оси расставляем как всегда справа, но начиная с плюса.

Исследуемая функция на промежутке (-5/3; 1) убывает, а на промежутках (-∞;-5/3) (1;+ ∞)

возрастает.

Точка х = -5/3 – точка максимума, х = 1 – точка минимума

Найдем значения функции в критических точках..

Для этого подставим значения критических точек в функцию f(x)= x³+x²-5x+3

f(-5/3)= (-5/3)³+(-5/3)²-5(-5/3)+3=-125/27+25/9+25/3+3=(-125+75+225)/27+3=175/27+3≈6,5+3≈9,5

В(-5/3; 9,5)-максимум

f(1)= 1³+1²-5·1+3=2-5+3=0

С(1;0)-минимум

5. Найдем точки перегиба и промежутки выпуклости, вогнутости функции.

Для этого найдем вторую производную данной функции:

f ''(x)=(3x²+2x-5)'=6х+2

f ''(x)=0; 6х+2=0; 6х=-2; х=-2/6; х=-1/3-точка подозрительная на перегиб

- +

-1/3

для , для

следовательно, график следовательно, график

функции на этом функции на данном

интервале выпуклый интервале выпуклый

вверх. вниз.

х = -1/3 - точка перегиба,

f(-1/3)= (-1/3)³+(-1/3)²-5(-1/3)+3=-1/27+1/9+5/3+3=(-1+3+45)/27+3=47/27+3≈1,74+3≈3,7

D=(-1/3; 3,7)

6. По полученным данным строим график

у

Задания для самостоятельной работы:

Вариант 1	Вариант 2.
Построить график функции: 1. 2. y =	Построить график функции: 1. 2. y =

Тема 1.2 Неопределенный интеграл.

Практическая работа №4

Нахождение неопределенного интеграла

Учебная цель: уметь находить неопределенный интеграл методами непосредственного интегрирования

Учебные задачи:

1) провести тест по теме «Неопределенный интеграл»

2) совместно рассмотреть выполнение заданий на вычисление неопределенного интеграла.

3) выполнить задания на самостоятельное нахождение неопределенных интегралов

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить дифференциал функции

- находить неопределенный интеграл методом непосредственного интегрирования

знать:

- таблицу основных неопределенных интегралов

- свойства неопределенного интеграла

- формулы дифференцирования

- формулу интегрирования по частям

Задачи практической работы

1. Повторение теоретического материала

2. Объяснение заданий на интегрирование функций

3. Самостоятельное выполнение заданий на интегрирование функций.

Содержание работы:

Таблица основных неопределенных интегралов

1. 2. 3. 4. 5. 6.

7. 8. 9. 10. 11. 12.

13. 14. 15. 16.

Непосредственное интегрирование

Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.

При непосредственном интегрировании применяются свойства неопределенного интеграла, таблица неопределенных интегралов и, если это необходимо, алгебраические преобразования

Пример вычисления 1:

Вычислите

Решение: Для вычисления интеграла сначала воспользуемся 2 и 3 свойствами неопре­деленного интеграла, а затем применим 1 и 4 табличные интегралы:

Пример вычисления 2:

Вычислите

Решение: Для вычисления интеграла сначала каждый член числителя почленно разделим на знаменатель, затем воспользуемся 2 и 3 свойствами неопре­деленного интеграла и применим 1 и 3 табличные интегралы

Задания для самостоятельной работы:

Вариант 1	Вариант 2.
Вычислите интегралы 1. 2. dx 3. dx 4. dx 5. dx	Вычислите интегралы 1. 2. . dx 3. dx 4. dx 5. dx

Тема 1.2 Неопределенный интеграл.

Практическая работа №5

Интегрирование функций

Учебная цель: уметь находить неопределенный интеграл методами непосредственного интегрирования, интегрирования методом подстановки, интегрирования по частям.

Учебные задачи:

1) провести тест по теме «Неопределенный и определенный интеграл»

2) совместно рассмотреть выполнение заданий на вычисление неопределенного интеграла различными методами.

3) выполнить задания на самостоятельное нахождение неопределенных интегралов

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить дифференциал функции

- находить неопределенный интеграл методом непосредственного интегрирования

- находить неопределенный интеграл методом подстановки

- находить неопределенный интеграл методом интегрирования по частям

знать:

- таблицу основных неопределенных интегралов

- свойства неопределенного интеграла

- формулы дифференцирования

- формулу интегрирования по частям

Задачи практической работы

1. Повторение теоретического материала

2. Объяснение заданий на интегрирование функций

3. Самостоятельное выполнение заданий на интегрирование функций.

Содержание работы:

Таблица основных неопределенных интегралов

1. 2. 3. 4. 5. 6.

7. 8. 9. 10. 11. 12.

13. 14. 15. 16.

1. Непосредственное интегрирование

Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.

При непосредственном интегрировании применяются свойства неопределенного интеграла, таблица неопределенных интегралов и, если это необходимо, алгебраические преобразования

2. Метод замены переменной (метод подстановки)

Он является одним из наиболее эффективных и распространенных приемов интегри­рования, позволяющих во многих случаях упростить вычисление интеграла. Суть этого ме­тода состоит в том, что путем введения новой переменной интегрирования заданный инте­грал сводится к новому интегралу, который легко вычисляется непосредственным интегри­рованием.

Пример вычисления 1: С развернутым оформлением

Вычислите

Решение:

Введем новую переменную t = 3x-4, тогда , откуда . Подставим новую переменную в интеграл (вместо выражения 3х-4 подставим t, вместо подставим ).

Далее нужно вернуться к первоначальной переменной. Для этого сделаем обратную замену (вместо t подставим выражение 3х-4), получим окончательный ответ.

Пример вычисления 2:

С кратким оформлением

Решение:

3. Интегрирование по частям

Формула интегрирования по частям

∫ udv = uv - ∫ vdu.        

Пример вычисления 1:

С развернутым оформлением

Вычислить

Решение. Полагая, что

находим

Пример вычисления 2:

С кратким оформлением

Вычислить ∫ (3х+2)lnxdx

)=(3x²/2+2x)lnx-∫(3x²/2+2x) 1/xdx=

∫

u=lnx, du=(lnx)'=1/xdx

dv=(3x+2)dx, v=∫(3x+2)dx=3x²/2+2x

(3х+2)lnxdx=(

⁼(3x²/2+2x)lnx-∫(3x²/2+2x) 1/xdx=(3x²/2+2x)lnx-∫(3x/2+2) dx= (3x²/2+2x)lnx-3x²/4-2x+C

Задания для самостоятельной работы:

Вариант 1	Вариант 2.
Вычислите интегралы 1. 2. ∫ сos8xsinxdx 3. ∫ (3x-7)9dx 4. ∫ (4х-5)lnxdx 5. ∫ xsinxdx	Вычислите интегралы 1. 2. ∫ sin6xsinxdx 3. ∫ (8x+5)12dx 4. ∫ (6х-3)lndx 5. ∫ xсosxdx

Тема 1.2 Определенный интеграл

Практическая работа №6

Вычисление определенного интеграла.

Учебная цель: уметь вычислять определенный интеграл с помощью формулы Ньютона-Лейбница и вычислять площадь криволинейной трапеции.

Учебные задачи:

1) провести письменный опрос по таблице основных интегралов

2) совместно рассмотреть выполнение заданий на вычисление определенного интеграла и нахождение площади криволинейной трапеции

3) выполнить задания на самостоятельное вычисление определенного интеграла и нахождение площади криволинейной трапеции

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- вычислять определенный интеграл

- строить график функции и выделять криволинейную трапецию на чертеже

- вычислять площадь криволинейной трапеции

знать:

- таблицу основных неопределенных интегралов

- формулу Ньютона-Лейбница

- понятие криволинейной трапеции

Задачи практической работы

1. Повторение таблицы основных неопределенных интегралов

2. Объяснение заданий на вычисление определенного интеграла и площади криволинейной трапеции.

3. Самостоятельное выполнение заданий на вычисление определенного интеграла и площади криволинейной трапеции.

.

Содержание работы:

Определенный интеграл вычисляется по следующей формуле:

Формула Ньютона-Лейбница

Пример вычислений 1:

Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b

Площадь криволинейной трапеции, ограниченной непрерывной кривой у=f(х), двумя прямыми х=а и х=b и осью абсцисс, вычисляется с помощью определенного интеграла по формулам:

Пример вычислений 2:

Вычислите площадь фигуры, ограниченной линиями , осями координат и прямой х=2.

Решение: Построим данные линии

Найдем точки пересечения графика функции с осью Ох: , ,

Задания для самостоятельной работы:

Вариант 1	Вариант 2	Вариант 3
Вычислите определенный интеграл	Вычислите определенный интеграл	Вычислите определенный интеграл
Вычислите площадь фигуры, ограниченной линиями	Вычислите площадь фигуры, ограниченной линиями	Вычислите площадь фигуры, ограниченной линиями
у = х2+4х, прямой х=3 и осями координат	у = 2-х2 , прямой х=-1 и осями координат	у = 4х - х2, прямой х=1 и осями координат

Тема 1.3 Дифференциальные уравнения I порядка

Практическая работа №7

Дифференциальные уравнения первого порядка

Учебная цель: уметь решать дифференциальные уравнения первого порядка с разделенными и разделяющимися переменными.

Учебные задачи:

1) провести математический диктант по дифференциальным уравнениям

2) совместно рассмотреть выполнение заданий на решение дифференциальных уравнений

3) выполнить задания на решение дифференциальных уравнений

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- решать дифференциальные уравнения с разделенными переменными

- решать дифференциальные уравнения с разделяющимися переменными

знать:

- таблицу основных неопределенных интегралов

- методы решения различных алгебраических уравнений

Задачи практической работы

1. Повторение теоретических основ темы «Дифференциальные уравнения»

2. Объяснение заданий на решение дифференциальных уравнений с разделенными и разделяющимися переменными.

3. Самостоятельное выполнение заданий на решение дифференциальных уравнений с разделенными и разделяющимися переменными

Содержание работы:

Уравнением с разделенными переменными называется дифференциальное уравнение вида

f(x)dx + g(y)dy = 0

с непрерывными функциями f(х) и g(y).

Равенство

где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Пример1. Решите дифференциальное уравнение у⁴dy=6 ^хdx

Решение: ∫у⁴dy=∫6 ^хdx

у⁵/5=6^х/ln6+C

у⁵=5·6^х/ln6+C

у=⁵√5·6^х/ln6+C Ответ: у=⁵√5·6^х/ln6+C

Дифференциальное уравнение называется уравнением с разделяющимися переменными, если его можно записать в виде

или

Пример 2. Решите дифференциальное уравнение dy/y=х ²dx

Решение: ∫dy/y=∫х ²dx

lny=x³/3+C

e^lny=e ^x³/3+C

y=e ^x³/3+C Ответ: y=e ^x³/3+C

Пример 3. Решите дифференциальное уравнение y'=5+x³

Решение: т.к. y'=dy/dx

dy/dx=5+x³

dy=(5+x³)dx

∫dy=∫(5+x³)dx

y=5x+x⁴/4+C Ответ: y=5x+x⁴/4+C

Задания для самостоятельной работы:

I вариант:	II вариант:
Решите дифференциальные уравнения	Решите дифференциальные уравнения
1. у3dy=cosxdx 2. dy/y=4xdx 3. y'=1+x2	1. у2dy=sinxdx 2. dy/y=x4dx 3. y'=3-x2

Тема 1.3 Дифференциальные уравнения I порядка

Практическая работа №8

Частные решения дифференциальных уравнений

Учебная цель: уметь решать дифференциальные уравнения с заданными начальными условиями

Учебные задачи:

1) провести математический диктант по дифференциальным уравнениям

2) совместно рассмотреть выполнение заданий на решение дифференциальных уравнений

3) выполнить задания на решение дифференциальных уравнений

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- находить общее и частное решение дифференциального уравнения

знать:

- таблицу основных неопределенных интегралов

- методы интегрирования

Задачи практической работы

1. Повторение теоретических основ темы «Дифференциальные уравнения»

2. Объяснение заданий на нахождение общего и частного решения дифференциального уравнения.

3. Самостоятельное выполнение заданий на нахождение общего и частного решений дифференциального уравнения

Содержание работы:

Пример . Найдите решение, удовлетворяющее начальному условию y'-y·(x-3)=0 y(2)=1

Решение: y'=y·(x-3)

т.к. y'=dy/dx

dy/dx= y·(x-3)

dy/ y =(x-3) dx

∫dy/ y =∫(x-3) dx

ln y =x²/2-3x+C

e^lny=e ^x²/2-3x+C

у=e ^x²/2-3x+C

Найдем решение при условии y(2)=1: у(2)=e ^1²/2-3·1+C=е^1/2-3+С= е^-2,5+С

е^-2,5+С=1, е^-2,5+С=е⁰, -2,5+С=0, С=2,5

Ответ: у=e ^{х²/2-3x+2,5}

Задания для самостоятельной работы:

I вариант:	II вариант:
Найдите решение, удовлетворяющее начальному условию	Найдите решение, удовлетворяющее начальному условию
1. у2dy=cosxdx у(π)=0 2. dy/y=2хdx у(0)=1 3. y'=1+x2 у(1)=0 4. y'+y·sinx=0 y(π/2)=2	1. у2dy=sinxdx у(π/2)=0 2. dy/y=x4dx у(0)=1 3. y'=3-x2 у(1)=0 4. y'-y·cosx=0 y(π)=1

Тема 1.3 Дифференциальные уравнения II порядка

Практическая работа №9

Линейные дифференциальные уравнения второго порядка с

постоянными коэффициентами

Учебная цель: уметь решать дифференциальные уравнения второго порядка с постоянными коэффициентами

Учебные задачи:

1) провести тест по дифференциальным уравнениям

2) совместно рассмотреть выполнение заданий на решение дифференциальных уравнений второго порядка

3) выполнить задания на решение дифференциальных уравнений второго порядка

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- составлять характеристическое уравнение

- решать квадратные характеристические уравнения

- решать дифференциальные уравнения второго порядка с постоянными коэффициентами

знать:

- понятие характеристического уравнения

- формулу дискриминанта

- формулы множества решений дифференциального уравнения

Задачи практической работы

1. Проверка теоретических основ темы «Дифференциальные уравнения»

2. Объяснение заданий на решение дифференциальных уравнений второго порядка.

3. Самостоятельное выполнение заданий на решение дифференциальных уравнений второго порядка.

Содержание работы:

Алгоритм решения линейных однородных дифференциальных уравнений второго порядка с постоянными коэффициентами.

Дифференциальное уравнение
Характеристическое уравнение
Дискриминант
Корни характеристического уравнения
Множества решений

Пример 1. Решить уравнение

Характеристическое уравнение:

Общее решение:

Пример 2. Решить уравнение

Характеристическое уравнение:

Общее решение:

Задания для самостоятельной работы

I вариант:	I I вариант:	I I I вариант:
Решите уравнения 2го порядка
а) б)	а) б)	а) б)

Раздел 2. Основы дискретной математики

Тема 2.1 Множества. Отношения

Практическая работа №10 Решение задач с применением теории множеств

Цель работы: сформировать умение выполнять операции с множествами

Содержание работы:

Теоретические сведения

Множество – одно из основных понятий математики.

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п.

Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.

Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит).

Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

Множество может быть задано одним из двух способов: перечислением и с помощью определяющего свойства.

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.

Например, если А={1,2,3,4}, B={3,1,4,2} то А=В.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.

Например, если А={1,2,4}, B={3,4,5,6}, то А ∪ B = {1,2,3,4,5,6}

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В.

Например, если А={1,2,4}, B={3,4,5,2}, то А ∩ В = {2,4}

Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.

Например, если А={1,2,3,4}, B={3,4,5}, то АВ = {1,2}

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).

Например, если А={1,2,3,4}, B={3,4,5,6}, то А Δ В = {1,2} ∪ {5,6} = {1,2,5,6}

Свойства:

Свойства перестановочности:

A ∪ B = B ∪ A

A ∩ B = B ∩ A

Сочетательное свойство:

(A ∪ B) ∪ C = A ∪ (B ∪ C)

(A ∩ B) ∩ C = A ∩ (B ∩ C)

Задания практической части:

1. Задание «С миру по нитке».Сначала надо восстановить шесть слов (половина букв уже вписана), а после из секторов, от которых отходят стрелки, нужно взять буквы и поместить в центральную фигуру. У вас получится главное слово задания (фамилия основоположника теории множеств)!

1. Упражнение «Найди пару»

∩ пустое множество

В(А) мощность множества А

U пересечение

Ø объединение

Ᾱ булеан множества А

|А| универсальное множество

\ дополнение

U разность

1. Определить в каких отношениях находятся между собой три множества:

1) А{1, 3}; B – множество нечетных положительных чисел; С – множество решений уравнения X²4X+3=0.

2) A={1, 2, 3}; B={2, 3}; C – множество решений уравнения Х1=0.

3) U={1, 2, 3, … , 20}, A – множество четных чисел, В – множество нечетных чисел.

4) А – множество решений уравнения 2Х²8X+6=0; В – множество решений уравнения X-1=0; N – множество натуральных чисел.

5) A={a, b, c}; B={a, b, d}; C={b, c}.

6) A={a, b}; B={a, c}; C={a, b, c}.

7) A={a}; B={{a}, {b}}; C={b}.

8) A – множество решений уравнения Х5=0; В  множество решений уравнения Х²9=0; C={{5}, {3}}.

9) A – множество решений уравнения X²4X+3=0; B={{1}, {3}}; C – множество нечетных натуральных чисел.

10) A={a, b, c}; B={{c}}; C={c}.

11) A={a, b}; B={b, c}; C={a}.

12) A={a}; B={b}; C={a, b, c}.

1. Приняв множество первых 20 натуральных чисел в качестве универсума U, запишите его подмножества: А – четных чисел; В – нечетных чисел; С – квадратов чисел; D – простых чисел; и запишите множества, которые получатся в результате следующих операций:

1) АВ; 2) АВ; 3) АС; 4) АD; 5) C – А; 6) C – В; 7) C+D; 8) U – A;

9) U – B; 10) U – D; 11) U – A; 12) AB.

Раздел 2. Основы дискретной математики

Тема 2.2 Основные понятия теории графов

Практическая работа №11 Решение задач с применением теории графов

Цель работы: закрепить знания о теоретико-множественном и графическом представлениях графов, сформировать практические умения решения задач с применением графов.

Содержание работы:

Теоретические сведения

Графические представления – удобный способ иллюстрации содержания различных понятий, относящихся к другим способам формализованных представлений (например, диаграммы Венна и другие графические иллюстрации основных теоретико-множественных и логических представлений).

Мощным и наиболее исследованным классом объектов, относящихся к графическим представлениям, являются так называемые графы, изучаемые в теории графов.

Теория графов – это раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами. Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.

Теория графов многократно переоткрывалась разными авторами при решении различных прикладных задач.

1. Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку (рис. 3.1). Эта задача была решена Эйлером в 1736 году.

Рис. 1. Иллюстрация к задаче о Кенигсбергских мостах

2. Задача о трех домах и трех колодцах. Имеется три дома и три колодца. Про­вести от каждого дома к каждому колодцу тропинку так, чтобы тропинки не пересекались (рис. 3.2). Эта задача была решена Куратовским в 1930 году.

Рис.2. Иллюстрация к задаче о трех домах и трех колодцах

Предметом первых задач теории графов были различные конфигурации, состоящие из точек и соединяющих их линий. При этом несущественно: являются ли эти линии прямыми или кривыми, длинными или короткими, тонкими или толстыми; важно только то, какие точки они соединяют. Т.о. граф – это абстрактное математическое понятие.

Графом в математике называется картинка из точек, соединенных отрезками (более строгое определение существует, но на практике никогда не требуется). Эти точки называются вершинами графа, а отрезки (они могут быть и кривыми; некоторые графы вообще невозможно нарисовать так, чтобы все соединения были прямыми) - ребрами графа. Две вершины, соединенные ребром, называются соседними. Последовательность ребер, соединяющих две вершины, называется путем.
Одинаковые по структуре графы называются изоморфными, при этом они могут рисоваться совершенно по-разному. Точное определение изоморфизма: вершины обоих графов можно занумеровать так, что две вершины в одном графе соседние тогда и только тогда, когда соседние две вершины с теми же номерами в другом графе. Например, изоморфизм графов, изображенных внизу, внешне неочевиден, но проверяется по определению.

Степенью вершины в графе называется число выходящих из нее ребер. В ориентированном графе у каждой вершины есть 2 степени: входящая (число ребер, входящих в вершину) и исходящая (число ребер, выходящих из вершины). Мы говорим, что вершина графа четная, если ее степень четна, и что вершина нечетная - в противном случае (в графе на рис. наверху все вершины четные). Для ориентированного графа понятие четности вершины обычно не вводится.
Назовем граф связным, если любые 2 вершины могут быть соединены путем из ребер. Несвязный граф состоит из нескольких кусков, каждый из которых связен. Такие куски называются компонентами связности. Любой связный граф состоит из одной компоненты связности - всего графа. Например, граф на рисунке сверху состоит из двух компонент связности: одна содержит вершины с номерами от 1 до 8, а вторая - вершину с номером 9. В ориентированном графы есть разные виды связности: односторонняя и двухсторонняя. Относительно последней граф тоже разбивается на компоненты связности.

Способы задания графов

Существуют три эквивалентных способа задания графов: аналитический, геометрический и матричный.

Аналитический способ задания графов: Граф GV,E задан, если задано множество элементов V и отображение E множеств V в V. Отображение Е может быть как однозначным, так и многозначным.

Геометрический способ задания графов: Множество элементов V графа G изображают кружками (это множество вершин), а отношение между ними – ребрами.

Матричный способ задания графов: Матрица, элементами которой являются нули и единицы, а также некоторое число m, называется матрицей смежности графа GV,E тогда и только тогда, когда её элементы образуются по следующему правилу: элемент , aij стоящий на пересечении vi  й строки и vj  го столбца, равен единице, если имеется ребро, идущее из вершины i v в вершину , j v и aij равен нулю в противном случае. Элемент aij равен единице, если при вершине i v имеется петля, и равен нулю в противном случае. Элемент aij равен некоторому числу m, где m – число рёбер графа, идущее из вершины i v в вершину j.

Эйлеровы графы.Понятие эйлерова графа связано со следующей задачей: можно ли нарисовать данный граф, не отрывая карандаш от бумаги и проводя каждое ребро ровно по разу? А можно ли так сделать, чтобы в конце карандаш вернулся в первую нарисованную вершину? Оказывается, как установил в XVIII веке Леонард Эйлер, существует очень простой критерий разрешимости этой задачи.
(?) А можно ли нарисовать, не отрывая карандаша, два графа на рисунке внизу?

Эйлеровым путем в графе называется путь, проходящий по всем ребрам графа ровно по разу. Существование эйлерова пути как раз и означает, что граф можно нарисовать, не отрывая карандаша от бумаги и проводя каждое ребро ровно по разу. Эйлеровым циклом называется такой тип эйлерова пути, в котором начальная и конечная вершины совпадают (то есть, здесь образуется цикл и в нем начальной вершиной можно считать любую). Существование эйлерова цикла означает, что граф можно нарисовать еще и так, чтобы карандаш вернулся в первую нарисованную вершину. Эйлеровым графом для краткости называют граф, содержащий эйлеров путь или эйлеров цикл.

Критерий Эйлера: В связном графе существует эйлеров путь тогда и только тогда, когда в нем не более 2-х нечетных вершин, а эйлеров цикл - тогда и только тогда, когда в нем все вершины четные.

Содержание практической работы

1. Для данного графа:

а) Составить матрицу смежности для графа.

б) Выписать вершины, смежные с вершиной 1.

в) Указать четные вершины графа

г) Составить матрицу инцидентности для графа.

д) Список ребер.

е) Указать ребра, инцидентные вершине 2.

2. Изобразите графически:

а) Неориентированное и ориентированное ребро;

б) Неориентированный граф G(V,E), заданный множеством V={v0, v1, v2, v3, v4, v5} E(v0)={v1,v2}={v0,v2,v4}; E(v1)={v0,v2,v4}; E(v2)={v0,v1,v5}; E(v3)={v4}; E(v5)={v2};

в) Плоский граф;

г) Полный неориентированный граф на трех, четырех и пяти вершинах;

д) Неполный ориентированный граф на пяти вершинах;

е) Петлю графа;

ж) Неориентированный и ориентированный мультиграф.

Раздел 3. Основы теории вероятностей и математической статистики

Тема 3.1 Основные понятия теории вероятностей

Практическая работа №12

Решение практических задач с применением вероятностных методов.

Учебная цель: уметь решать задачи на классическое определение вероятности, уметь находить числовые характеристики случайных величин.

Учебные задачи:

1) провести математический диктант по материалам лекций

2) совместно рассмотреть выполнение заданий на вычисление классической вероятности события и нахождение числовых характеристик случайных величин

3) выполнить задания на вычисление классической вероятности события и нахождение числовых характеристик случайных величин

Образовательные результаты, заявленные во ФГОС третьего поколения:

Студент должен

уметь:

- вычислять вероятность события по формуле классической вероятности

- составлять закон распределения случайной величины

- вычислять математическое ожидание случайной величины

- вычислять дисперсию и среднее квадратичное отклонение случайной величины

знать:

- формулу классической вероятности

- понятие случайной величины

- формулы вычисления математического ожидания, дисперсии и среднего

квадратичного отклонения

Задачи практической работы

1. Проверка теоретических основ темы «Основы теории вероятностей и математической статистики»

2. Объяснение заданий на вычисление классической вероятности события и нахождение числовых характеристик случайных величин.

3. Самостоятельное выполнение заданий на вычисление классической вероятности события и нахождение числовых характеристик случайных величин.

Содержание работы:

1. Классическая вероятность события:

Вероятностью Р(А) события А называют отношение числа благоприятствующих этому событию исходов m к общему числу n всех возможных элементарных исходов испытания, образующих полную группу, т.е Р(А) =

Свойства вероятности:

1. Вероятность достоверного события равна единице.

2. Вероятность невозможного события равна нулю.

3. Вероятность случайного события есть число, заключенное между нулем и единицей.

Таким образом, вероятность любого события А удовлетворяет неравенству 0 ≤ P(A) ≤ 1.

Задача 1.

Из 25 экзаменационных билетов, занумерованных числами от 1 до 25, наудачу извлекается один. Какова вероятность того, что номер вытянутого билета есть число, кратное трем?

Решение:

1. Всего 25 экзаменационных билетов. Следовательно, число всех возможных элементарных исходов испытания n=25.

2. Из 25 экзаменационных билетов, занумерованных числами от 1 до 25 чисел кратным трем всего 8 (3; 6; 9; 12; 15; 18; 21; 24). Следовательно, число благоприятствующих этому событию исходов m=8

3. По формуле классической вероятности Р(А) = находим Р(А)=8/25

Ответ: Р(А)=8/25

2.Числовые характеристики случайных величин

1. Случайной величиной называется числовая переменная величина, принимающая в зависимости от случая те или иные значения с определёнными вероятностями.

2.  Математическим ожиданием дискретной случайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений М(x) = x_ip_i = x₁p₁+ x₂p₂ + ... + x_np_n (1)

3. Дисперсией дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(x) = M(x – M(x))² (2) или или D(x) = M(x²) – (M(x))² (3)

4. Дисперсия случайной величины характеризует степень разброса значений случайной величины относительно её математического ожидания.

Средним квадратичным отклонением дискретной случайной величины называется квадратный корень из дисперсии: (x) = D(x) (4)

Пример1. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение числа очков, выпадающих при бросании игральной кости.

Решение. Случайная величина Х числа очков принимает значения1, 2, 3, 4,5, 6. Составим закон ее распределения:

Xi	1	2	3	4	5	6
Pi	1/6	1/6	1/6	1/6	1/6	1/6

Тогда математическое ожидание вычисляется по формуле (1):

Закон распределения случайной величины х²

Xi	1	4	9	16	25	36
Pi	1/6	1/6	1/6	1/6	1/6	1/6

Тогда M(x²)=1/6(1+4+9+16+25+36)=1/6∙91=91/6

По формуле (3) найдем дисперсию: D(x) = M(x²) – (M(x))²=91/6-(7/2)²=35/12=2,92

По формуле (4) вычислим среднее квадратичное отклонение

(x) = D(x)=√2, 92≈1,71

Ответ: М(х)=3,5; D(x)=2,92; (x) =1,71.

Задания для самостоятельной работы:

Вариант 1:

1. Какова вероятность того, что число на вырванном наудачу листке нового календаря равно 30, если в году 365 дней?

2. Для заданного закона распределения найти М(x), D(x), (x).

xi	0	3	5	8
pi	0.3	0.25	0.3	0.15

Вариант 2:

1. В урне 20 одинаковых по размерам и весу шаров, из ко­торых 5 красных и 15 синих. Из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется красным?

2. Для заданного закона распределения найти М(x), D(x), (x).

xi	0	3	5	8
pi	0.3	0.25	0.3	0.15

Порядок выполнения отчета по практическим работам

1. Практические работы выполняются в аудиторное время, согласно календарно-тематического плана

2. Практические работы выполняются в рабочей тетради

3. При выполнении практических работ во внеаудиторное время, при условии пропуска занятия по уважительной причине, необходимо защитить работу.

4. При выполнении практических работы во внеаудиторное время, при условии пропуска занятия по неуважительной причине, ставится оценка не выше «удовлетворительно».