Методические рекомендации по изучению темы «Параллельность прямых, прямой и плоскости», для студентов 1 курса

Занятие 88. Тема «Параллельность прямых, прямой и плоскости»

План лекции:

1. Взаимное расположение прямых в пространстве.

2. Параллельность прямых в пространстве.

3. Взаимное расположение прямой и плоскости.

4. Параллельность прямой и плоскости.

Взаимное расположение прямых в пространстве.

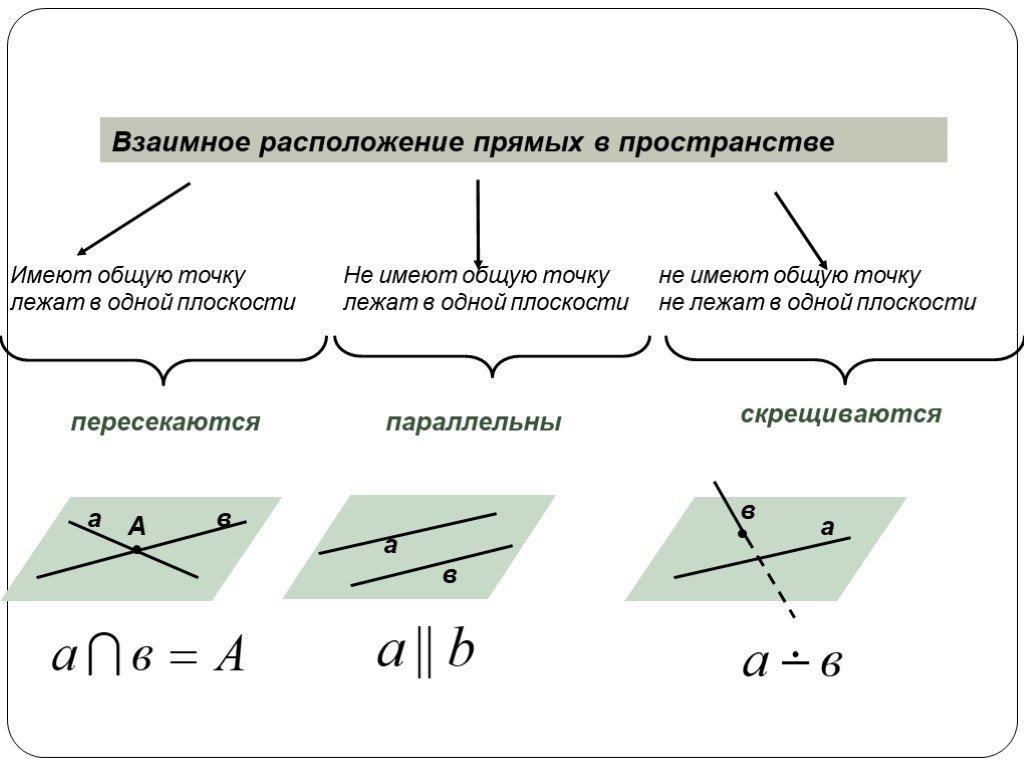
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельность прямых a и b обозначается так: a∥b или b∥a.

Две прямые называются скрещивающимися, не лежат в одной плоскости и не пересекаются.

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB и A₁D₁; AB и B₁C₁; CD и A₁D₁; CD и B₁C₁; BC и C₁D₁; BC и A₁B₁; AB и B₁C₁; AB и A₁D₁.

Параллельность прямых в пространстве.

Теорема. Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.

Теорема. Две прямые, параллельные третьей прямой, параллельны.

Взаимное расположение прямой и плоскости.

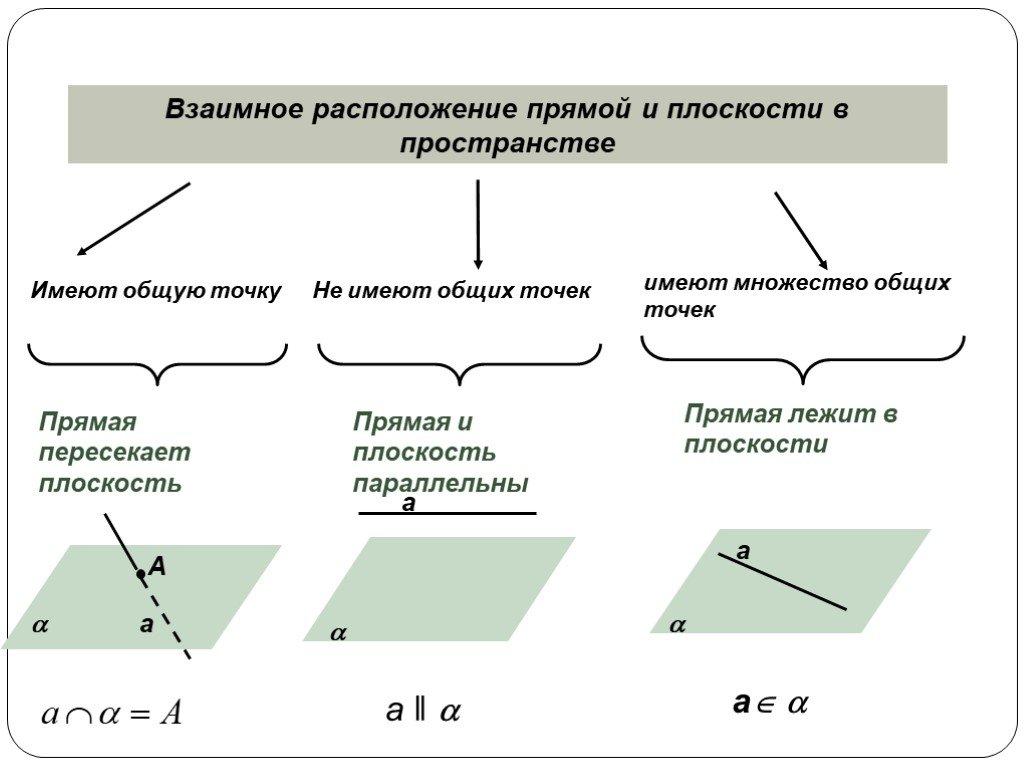
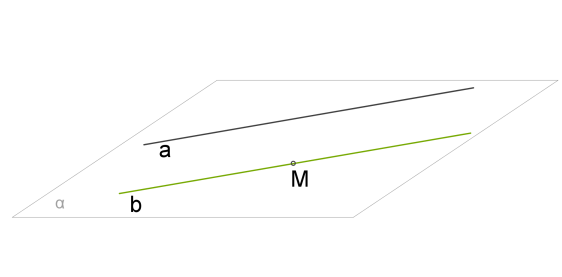
Параллельность прямой и плоскости.

Прямая и плоскость называются параллельными, если они не имеют общих точек.

Теорема. «Признак параллельности прямой и плоскости»
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

a‖b, bϵα = a‖α

Теорема. Если одна из двух параллельных прямых a∥b параллельна данной плоскости α , то другая прямая либо параллельна этой плоскости, либо лежит в этой плоскости. a‖b, a‖α = b‖α

Задание для самостоятельного выполнения

Задание 1. Сделать краткий конспект по данной теме.

Задание 2. Выучить все формулировки определений и теорем.

Задание 3.

Задание 4. Сделать рисунок и решить задачу:

Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А₁, В₁, М₁. Найдите длину отрезка ММ₁, если отрезок АВ не пересекает плоскость и если АА₁=5м, ВВ₁=7м.

Выполненные задания отправить на адрес электронной почты преподавателя: [email protected]. Имя файла – фамилия студента и номер занятия. (например, Петров-88)