Глава 2. «Треугольники». Методические рекомендации
Глава 2 учебника геометрии за 7 класс [11] связана с темой треугольниках. Рассматриваются виды треугольников, признаки равенства треугольников. Все уроки по данной теме проводились с использованием математической среды GeoGebra.
Рекомендации к построению задач
Решая задачи, которые связаны с темой «Треугольники», нужно помечать равенство сторон двух или более треугольников между собой. При решении задач на доске мы можем это сделать при помощи мела и руки, а как же это сделать в математической среде GeoGebra.
В GeoGebra также предусмотрена эта функция. Если в задаче (особенно на тему признаки равенства треугольников) обозначить равенство сторон нужно большее количество раз, то есть функция с выделения данной стороны и изменение ее стиля.
Приведем в качестве примера решение задачи №182.
182. На рисунке 148 прямые m и n – серединные перпендикуляры сторон АВ и АС треугольника АВС. Докажите, что точка О равноудалена от всех вершин данного треугольника.
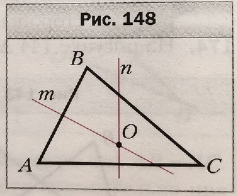
Рисунок . Рисунок 148 из учебника [11].
Учителю следует заранее подготовить соответствующий чертеж. Основная проблема состоит в том, что GeoGebra дает собственные названия точкам при построении, и её названия не соответствуют чертежу из учебника. Поэтому при построении чертежа стоит изменить название вершин.
В ходе решения задачи у нас появляется потребность в обозначении равенства некоторых сторон.
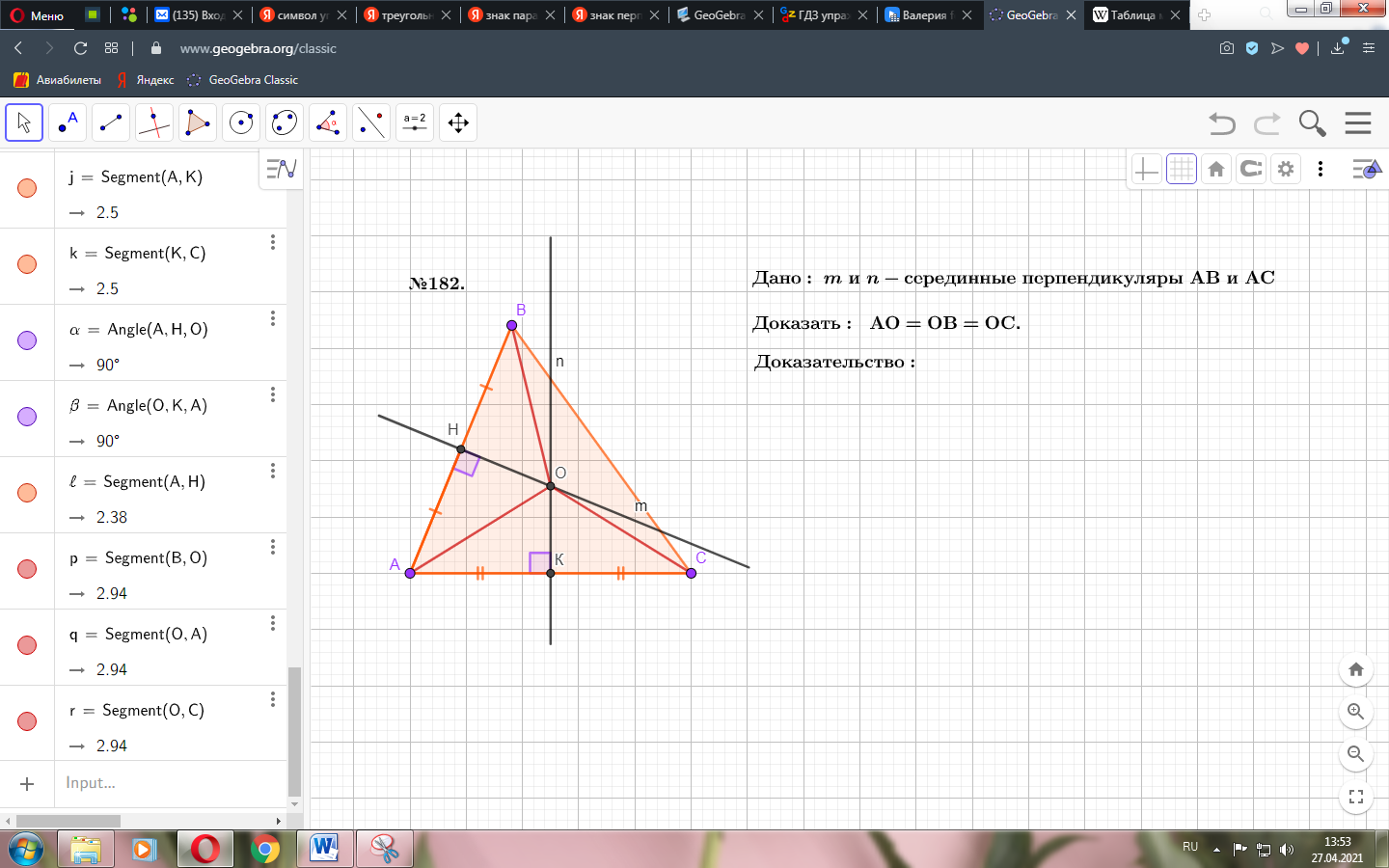
Рисунок . Условие задачи 182.
Для того чтобы это сделать выделяем нужную сторону, заходит в настройки, нажимаем стиль и выбираем нужные нам штрихи.
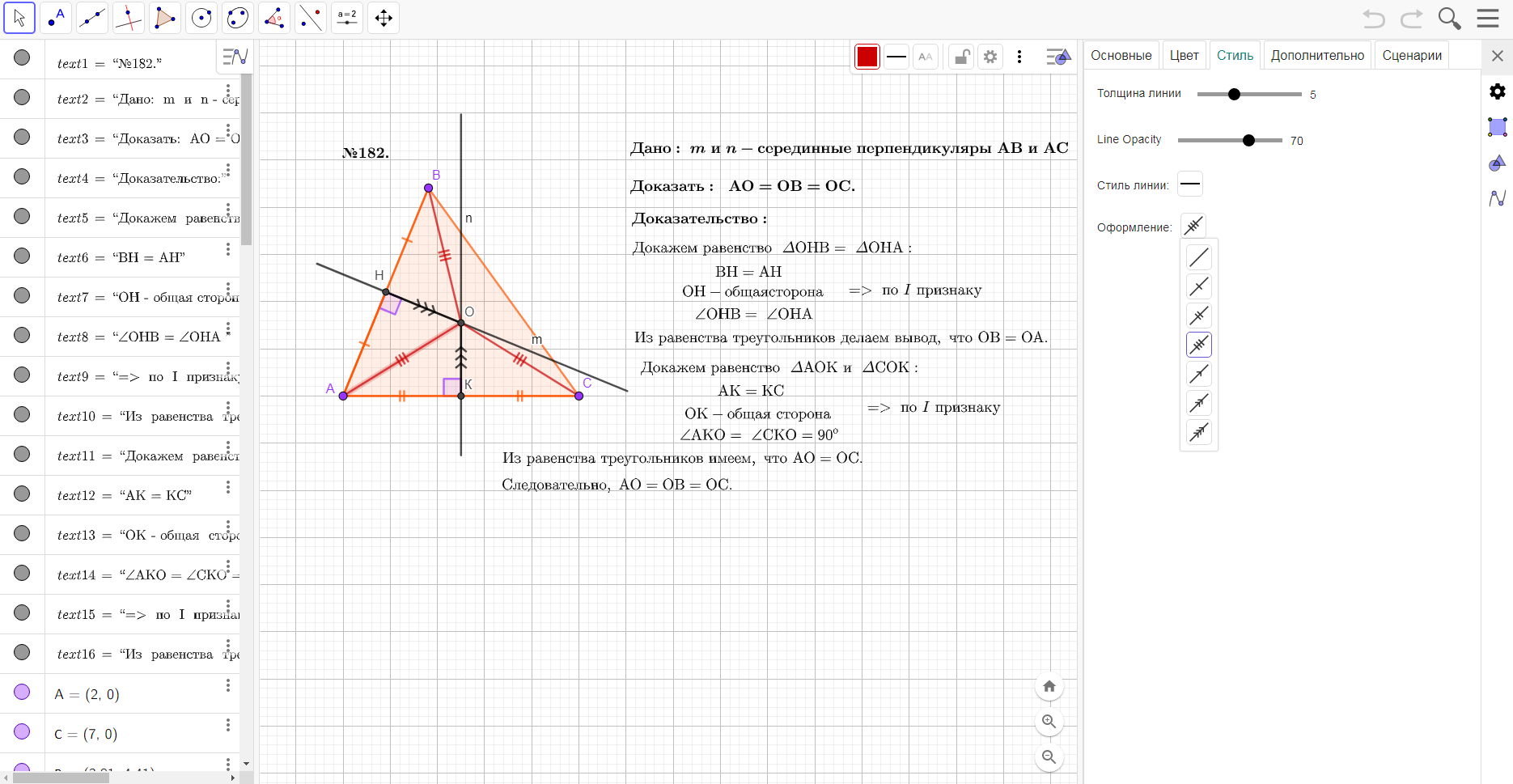
Рисунок . Равенство сторон (обозначение)
Поскольку в задачах могут быть не только равные стороны, но и углы, их также можно отмечать при решении задачи.
Рассмотрим еще один пример (задача №203).
203. В равнобедренном треугольнике АВС сторона АС – основания, ∠ВСА = 40о, ∠АВС = 100о, ВD – медиана. Найдите углы треугольника АВD.
В ходе решения задачи нам нужно было отметить углы разной величины. В курсе геометрии мы привыкли это делать дугами от одной до 3 штук. В GeoGebra есть такая функция. Достаточно выделить определенный угол, зайти в настройки, стиль и выбрать нужное оформление угла.
Рисунок . Равенство углов (обозначение).
Так как практически все задачи связаны с построением треугольников, то лучше всего, когда построили углы, параллельные и перпендикулярные прямые, биссектрисы и тд, обозначить получивший треугольник при помощи инструмента «polygon» для лучшей работы с ним.
Приведем пример обозначения треугольника из задачи №234.
234. В треугольнике АВС ∠АСВ = 90о, ∠А = ∠В = 45о, СК – высота. Найдите сторону АВ, если СК = 7 см.
При построении чертежа к задаче начинаем с углов, потом соединяем получившиеся точки прямыми. У нас получился треугольник.
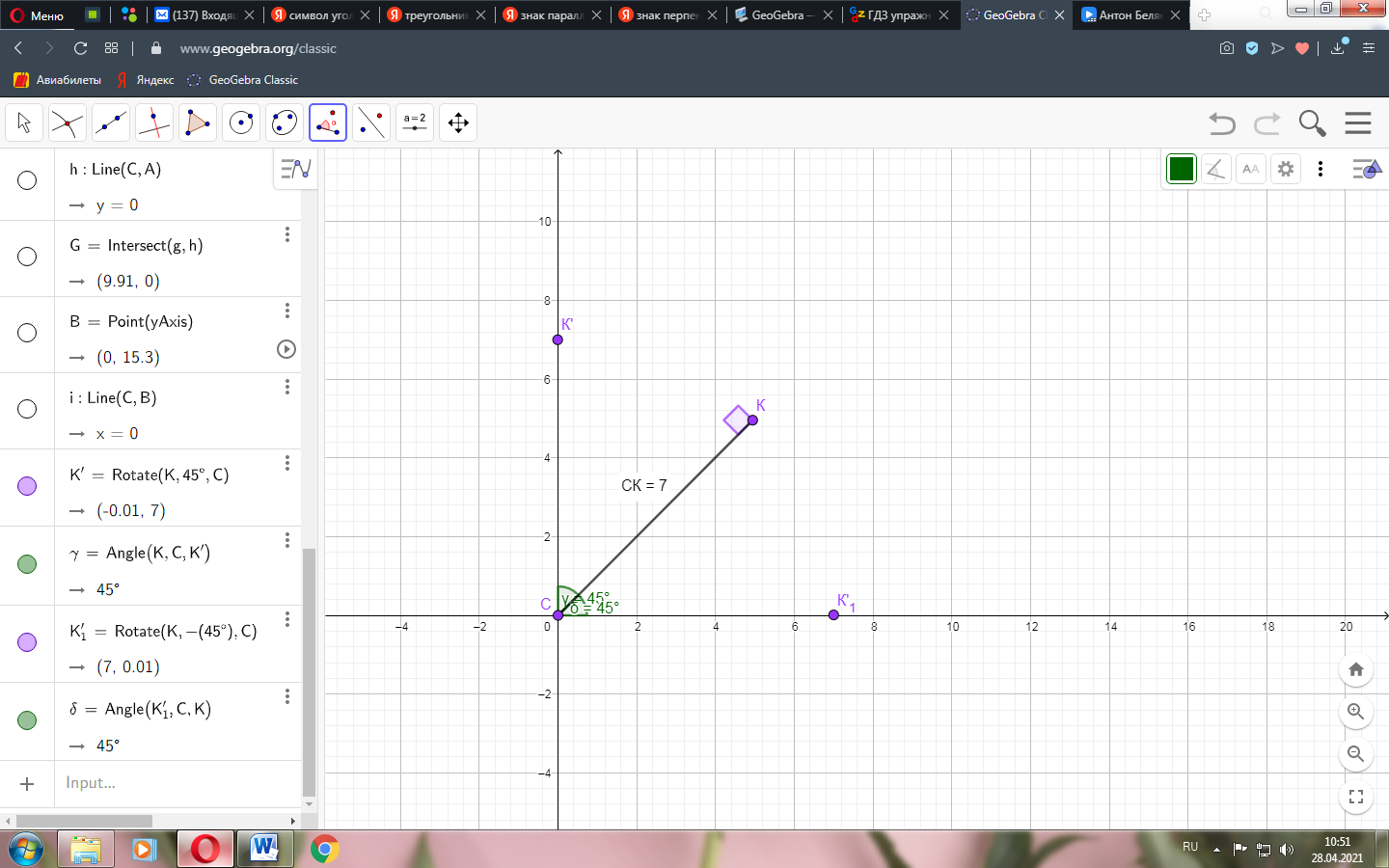
Рисунок . Начало построения.
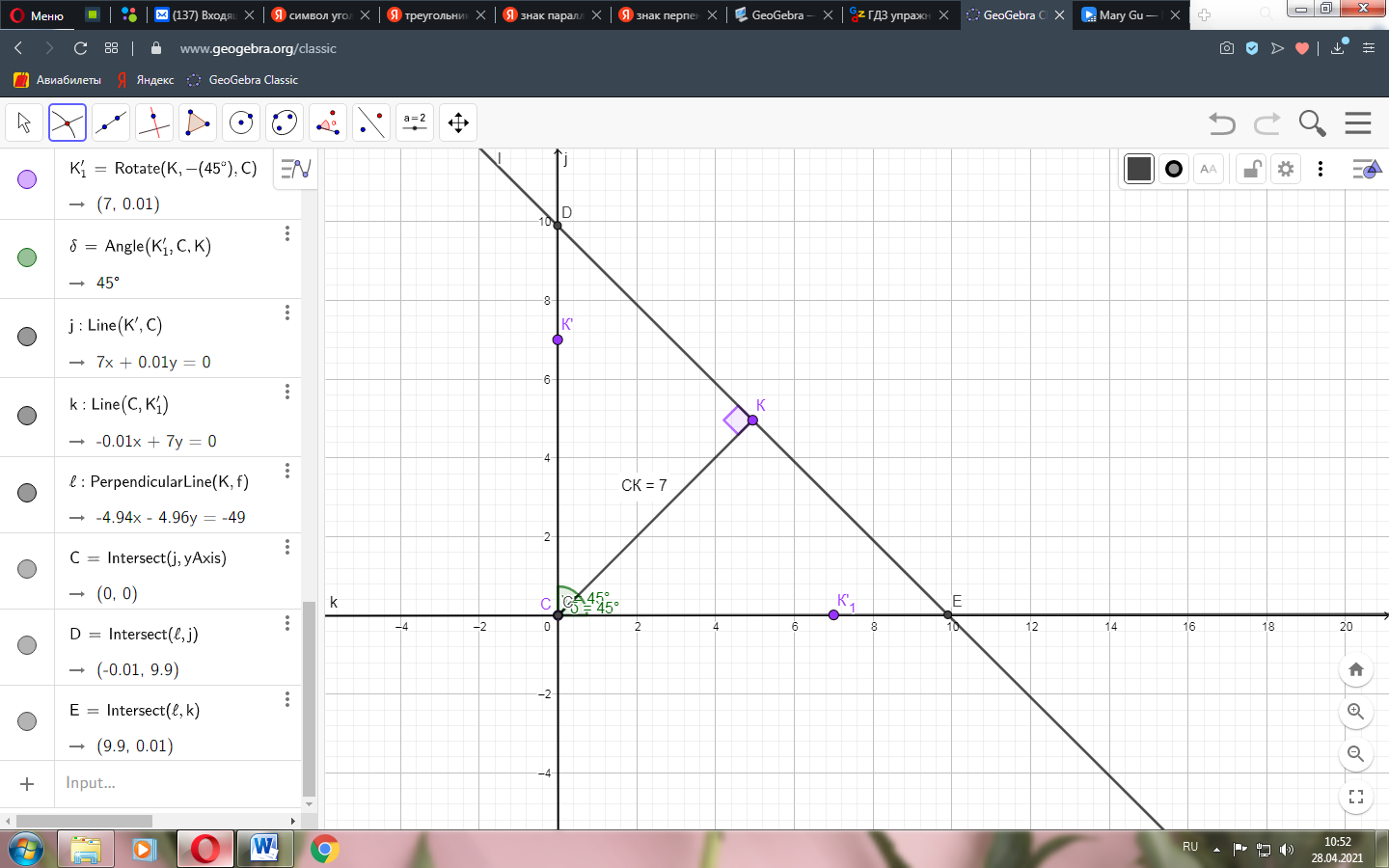
Рисунок . Построение треугольника.
Важно данный треугольник сделать цельным, чтобы в дальнейшем можно было работать с ним, как с геометрической фигурой. Для этого используем инструмент «polygon».
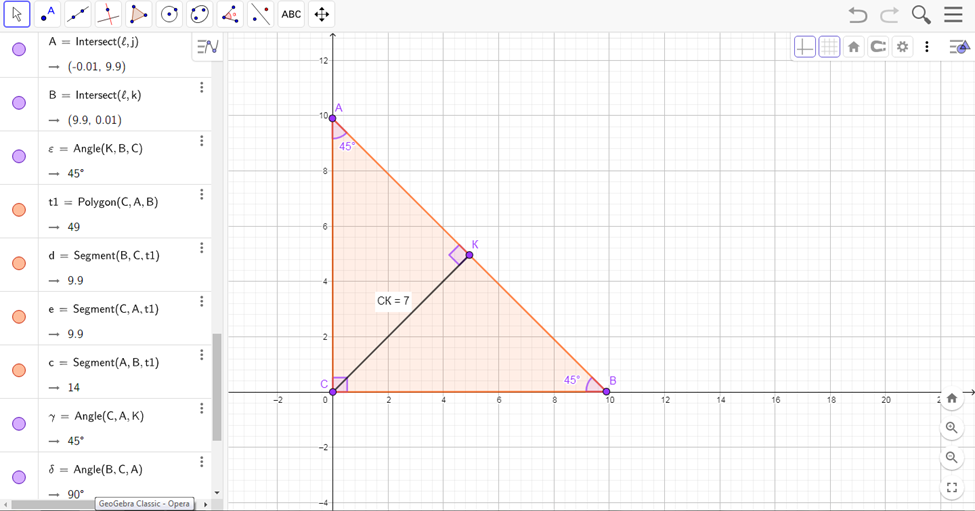
Рисунок . Чертеж для решения задачи.
Помимо произвольных треугольников, существую равнобедренные и равносторонние треугольники. Их построение имеет особое значение, так как это можно сделать несколькими способами.
Рассмотрим построение равнобедренного треугольника. Это можно сделать двумя способами: при помощи координатных осей Х и У или при помощи окружности.
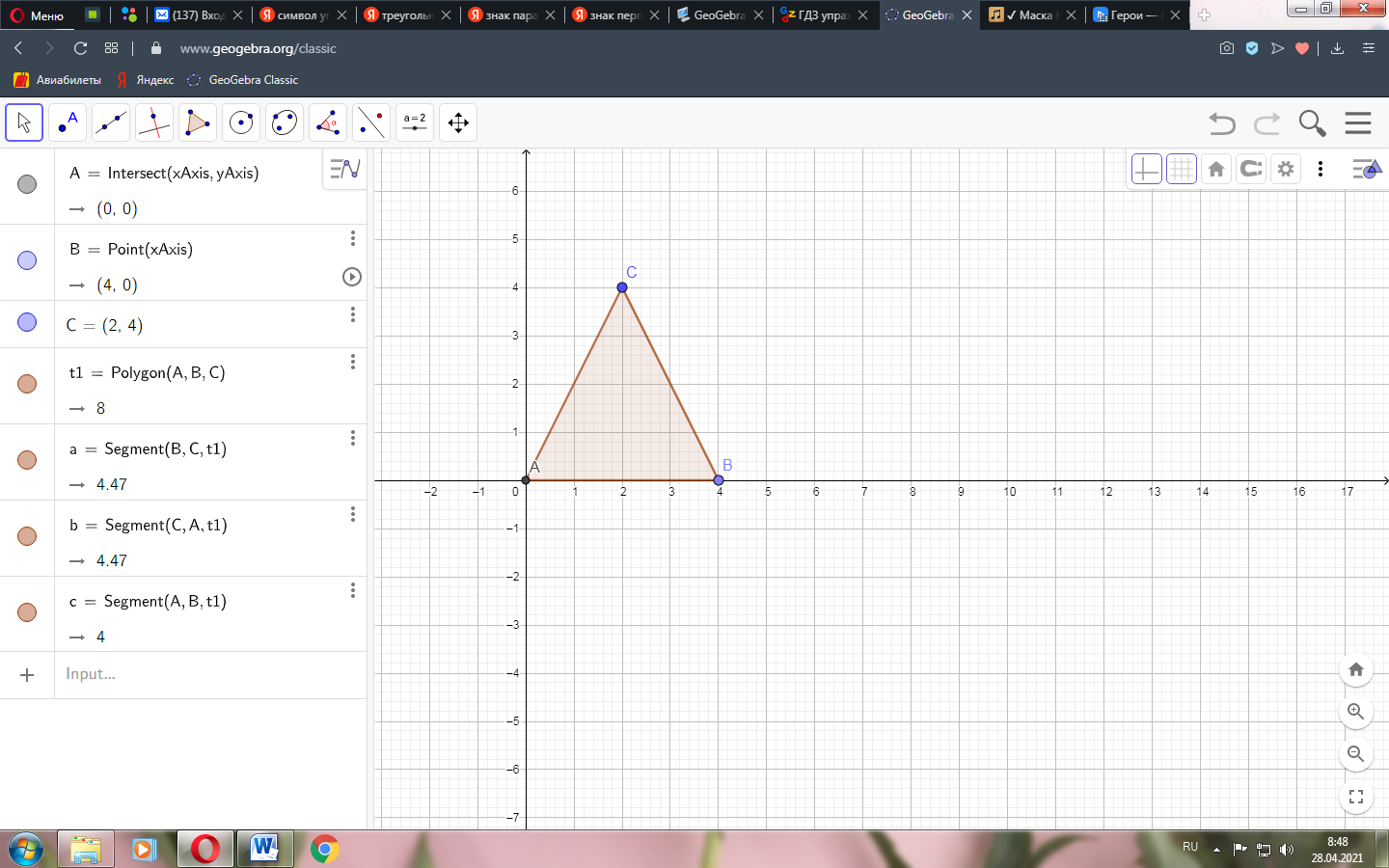
Рисунок . Построение треугольника при помощи осей Х и У.
Достаточно простой способ построения при помощи осей Х и У, нежели используя окружность. Для этого нужно построить окружность, отметить радиусы, далее соединив их получится равнобедренный треугольник.
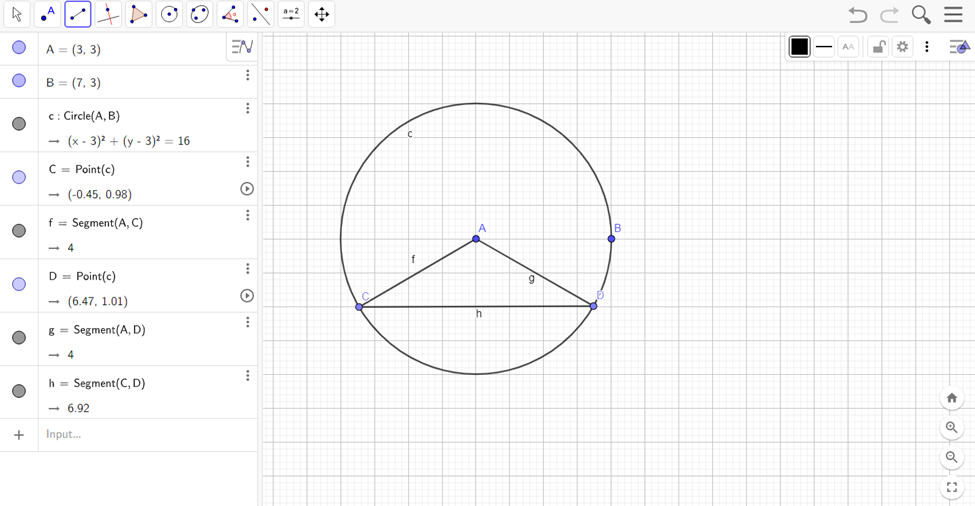
Рисунок . Построение окружности и радиусов.
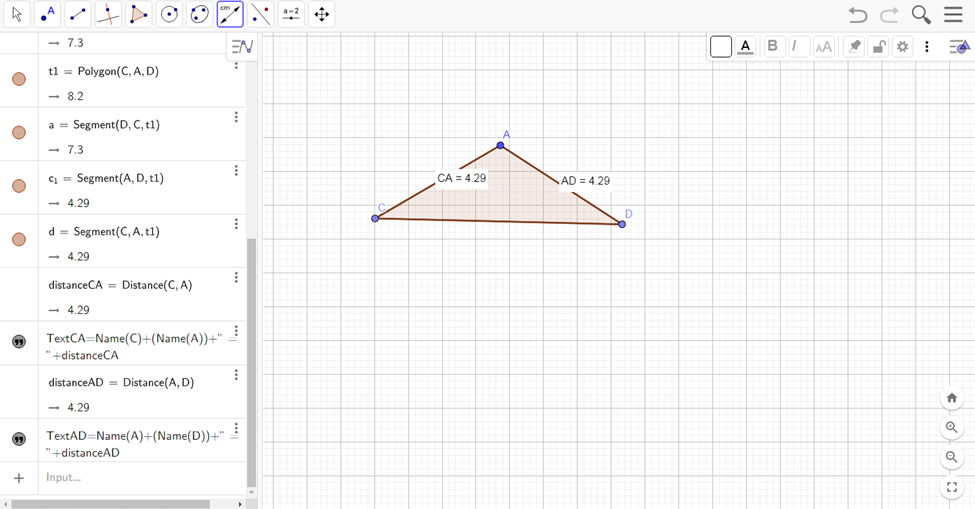
Рисунок . Равнобедренный треугольник.
Рассмотрим построение равностороннего треугольника двумя способами.
Первый способ нужно построить отрезок, потом провести две окружности центрами которых будут являться концы отрезка. Далее соединить их с точкой пересечения окружностей.
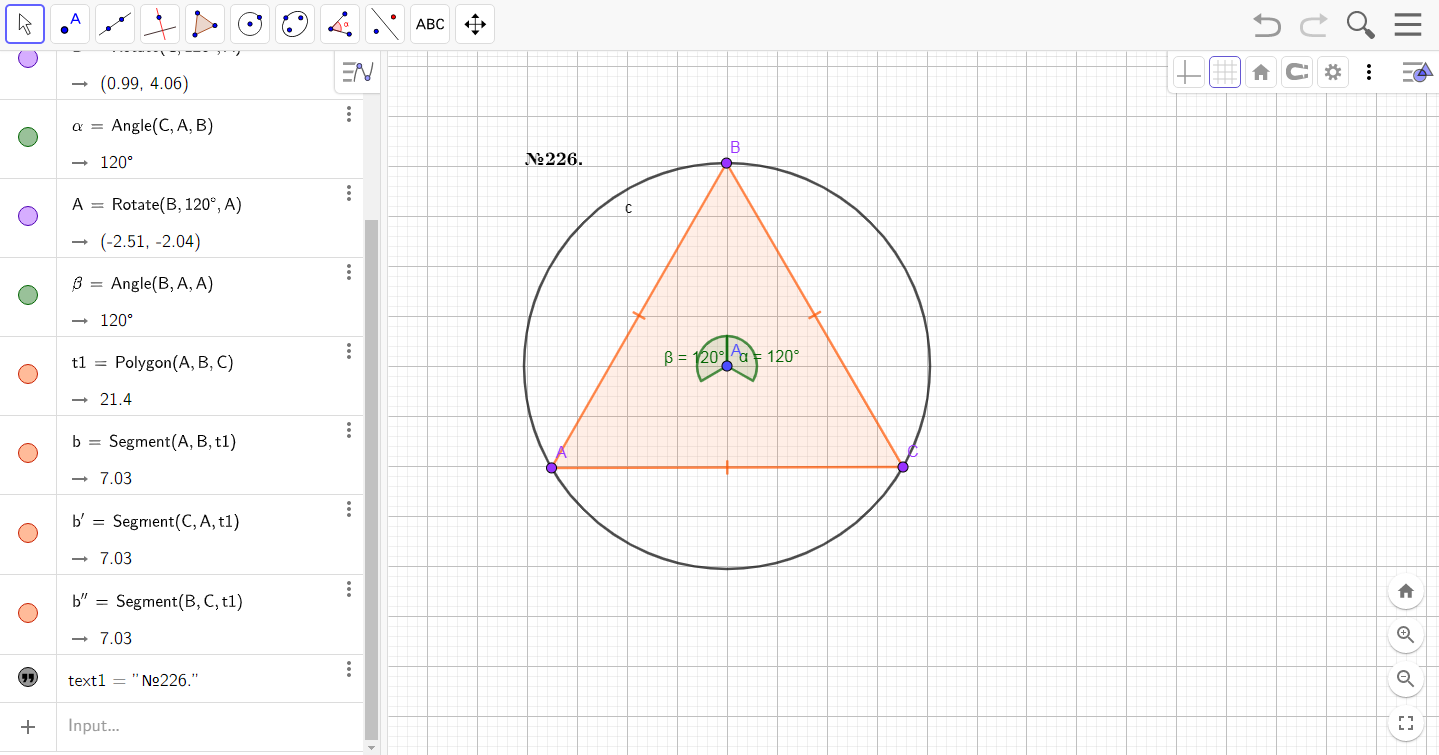
Рассмотрим пример из задачи №226.
226. На сторонах равностороннего треугольника АВС (рис. 164) отметили точки М, К и D так, что АD = ВМ = СК. Докажите, что ΔМКD равносторонний.
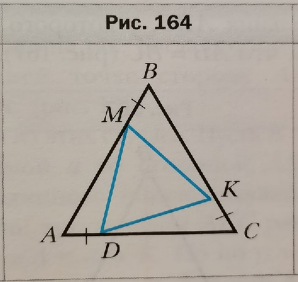
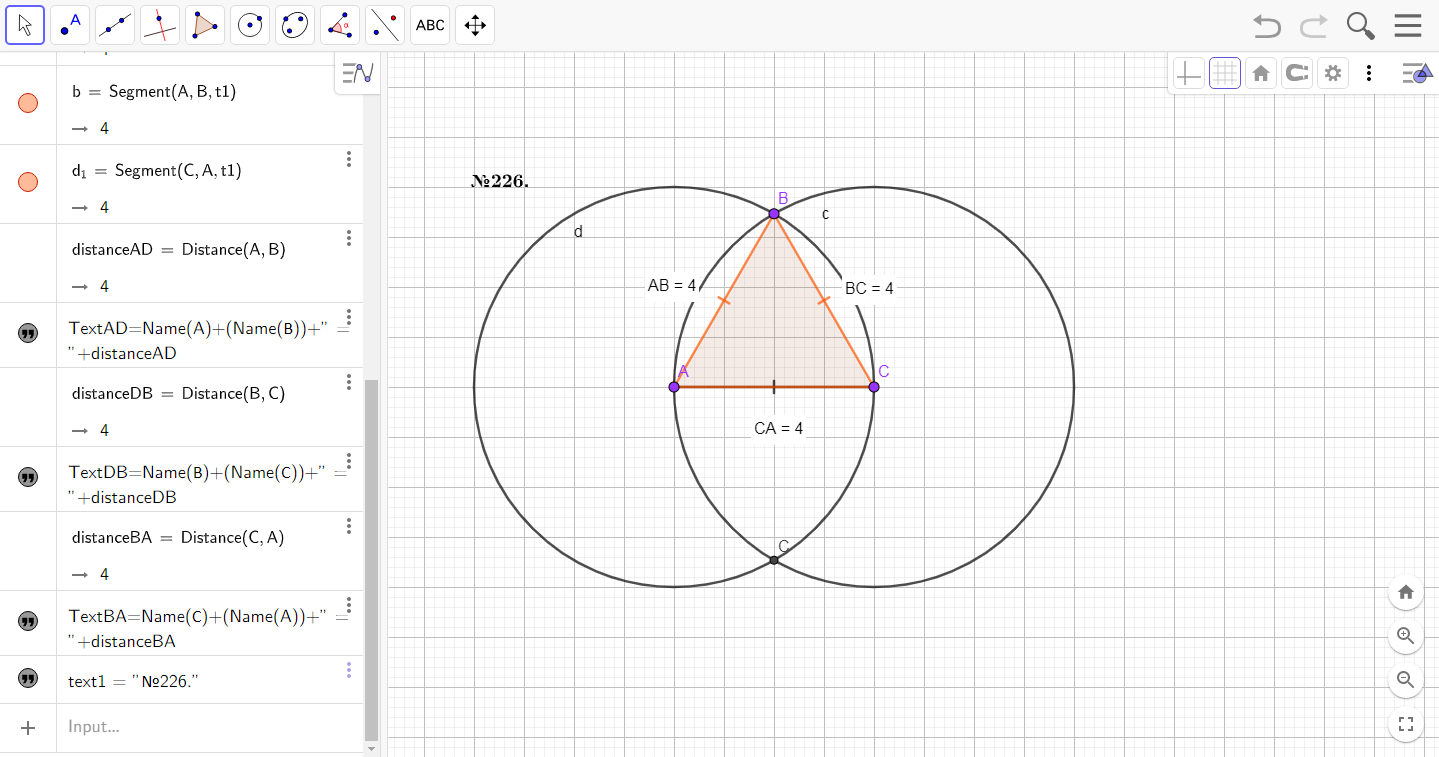
Рисунок . Построение равностороннего треугольника.
Способ второй связан также с окружность, но построим три угла в 120о. Так как в равностороннем треугольнике углы равны 60о, а они вписанные углы, значит, центральный угол равен 120о.
В список литературы
11. Геометрия: 7 класс : учебник для учащихся общеобразовательных организаций / А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. – М. : Вентана-Граф. 2015. – 192с. : ил. ISBN 978–5–360–05508-2





























