Методическое пособие для подготовки к олимпиадам по физике. Физтех 10 класс

2. U-образная трубка с открытыми в атмосферу вертикальными коленами заполнена частично ртутью. Одно из колен закрывают сверху, а в другое доливают слой ртути длиной l = 6 см. После установления равновесия в закрытом колене остаётся воздушный столб длиной L = 19 см. Найдите смещение уровня ртути в открытом колене относительно начального положения. Атмосферное давление p₀ = 760 мм рт. ст

3 . Поршень, который может двигаться в горизонтальном цилиндре без трения, делит его объём на две части. В одной части находится m₁ = 1 г водорода, а в другой — m₂ = 7 г азота. Температуры газов одинаковые. Какую часть объёма цилиндра занимает водород? Молярные массы водорода и азота: µ₁ = 2 г/моль, µ₂ = 28 г/моль.

2. Гелий в количестве ν моль расширяется от температуры T₁ в изобарическом процессе 1–2, а затем в процессе 2–3 с прямо пропорциональной зависимостью давления p от объёма V (см. рисунок). Отношение объёмов V₂/V₁ = V₃/V₂ = 3/2. 1) Найти температуры в состояниях 2 и 3. 2) Найти работу, совершённую газом в процессе 1–2–3. 3) Найти суммарное количество теплоты, полученное газом в процессе 1–2–3.

3 . Один моль гелия находится при температуре T = 273 K. Далее газ расширяется так, что объём увеличивается на 3%, а давление уменьшается на 2%. Изменения параметров газа считать малыми. 1) Вычислите приращение ∆T температуры газа. 2) Какую работу ∆A совершил газ в процессе расширения? 3) Найдите молярную теплоёмкость C газа в этом процессе.

4 . Тонкая Г-образная трубка постоянного внутреннего сечения полностью заполнена ртутью (см. рисунок). Горизонтальное колено трубки закрыто с одного конца. Вертикальное колено высотой H = 8 мм открыто в атмосферу. Атмосферное давление p₀ = 752 мм рт. ст. Ртуть начинает выливаться, если трубку двигать вдоль горизонтального колена с постоянным ускорением, не меньшим чем a₀ = 0,8g. При движении трубки с некоторым ускорением a, большим a₀, выливается слой ртути длиной L₁ = 19 см. 1) Найти длину L горизонтального колена. 2) Найти ускорение a.

3. На диаграмме зависимости давления P газа от температуры T для гелия в количестве ν = 3/2 моль показано, что сначала газ нагревался в изобарном процессе 1–2, а затем охлаждался в процессе 2–3 прямо пропорциональной зависимости давления от температуры. Температуры газа в состояниях 1, 2 и 3 T₁ = 150 К, T₂ = 3T₁, T₃ = 2T₁. Отношение давлений в состояниях 1 и 3 равно 3/2. 1) Найти работу газа в процессе 1–2–3. 2) Найти отношение количества теплоты, подведённого к газу в процессе 1–2, к количеству теплоты, отведённому от газа в процессе 2–3.

4. Поршень делит объём герметичного вертикально расположенного цилиндра на две части. Стенки цилиндра хорошо проводят теплоту. Снаружи цилиндра поддерживается постоянная температура T = 373 К. Поршень создаёт своим весом дополнительное давление p = p₀/5, где p₀ — нормальное атмосферное давление. Под поршнем в объёме V₀ = 1 л находится воздух, над поршнем в объёме V₀ — вода массой m₁ = 1,2 г и водяной пар. Система в равновесии. Цилиндр переворачивают вверх дном. После наступления равновесия под поршнем находится вода и водяной пар, над поршнем — воздух. 1) Найти объём пара в конечном состоянии. 2) Найти массу воды в конечном состоянии. Объём воды значительно меньше объёма цилиндра, масса воды значительно меньше массы поршня. Трением поршня о цилиндр пренебречь. Молярная масса водяного пара µ = 18 г/моль, универсальная газовая постоянная R = 8,31 Дж/(моль · K).

5. Одноатомный идеальный газ в количестве ν = 1 моль участвует в прямом циклическом процессе, составленном из двух изотерм и двух изохор. При изохорическом нагревании газ получает Q₁ = 1000 Дж теплоты, при изотермическом расширении газ получает ещё Q₂ = 500 Дж теплоты. Известно, что минимальная температура в процессе T₁ = 300 К. 1) Найти максимальную температуру T₂ газа в цикле. 2) Найти работу A газа при расширении. 3) Найти КПД η цикла.

2. Пустую стеклянную бутылку опускают в цилиндрический сосуд с водой с вертикальными стенками. Бутылка стала плавать, а уровень воды в сосуде поднялся на H₁ = 3 см. Затем в бутылку медленно наливают воду. Когда масса налитой воды достигает некоторой величины, бутылка начинает тонуть. Уровень воды в сосуде за время наливания поднялся ещё на H₂ = 1 см. Плотность стекла ρ₀ = 3 г/см³ , плотность воды ρ = 1 г/см³ . Площадь внутреннего сечения сосуда S = 250 см² . 1) Найти массу пустой бутылки. 2) Найти массу воды, налитой в бутылку. 3) Найти вместимость пустой бутылки

4. В цилиндре под поршнем находятся в равновесии воздух, водяной пар и вода. Отношение масс жидкости и пара α = 1/2. В медленном изотермическом процессе объём влажного воздуха увеличивается в k = 3 раза. 1) Найти относительную влажность воздуха ϕ₁ в цилиндре в начале процесса. 2) Найти относительную влажность воздуха ϕ₂ в цилиндре в конечном состоянии.

5. Одноатомный идеальный газ нагревается в изохорическом процессе 1–2, затем расширяется в адиабатическом процессе 2–3 и сжимается в изобарическом процессе 3–1 (см. рис.). Отношение работы газа A₂₃ в процессе 2–3 к работе над газом A₃₁ (A₃₁ 0) в процессе 3–1 A₂₃/ A₃₁ = 36/ 7 . В процессе сжатия объём газа уменьшается в 8 раз. 1) Найти отношение температур T₂/T₃ в состояниях 2 и 3. 2) Найти КПД цикла.

1. Горизонтальный цилиндр длины L 0,5 м вначале открыт в атмосферу и заполнен воздухом при температуре T₀ =300 K. Цилиндр плотно закрывают тонким поршнем и охлаждают. Поршень смещается и останавливается на расстоянии h 0, 4 м от дна. Далее цилиндр нагревают до температуры T₀ , при которой поршень останавливается на расстоянии H 0, 46 м от дна. Атмосферное давление P₀ =100 кПа, площадь поперечного сечения цилиндра S 0,1 м ² . Внутренняя энергия воздуха U PV , где P – давление, V - объем. Считать силу трения, действующую на поршень, постоянной в процессе движения поршня. 1) До какой температуры T₁ был охлажден воздух в цилиндре? 2) Найдите силу трения F_TP , действующую на поршень в процессе движения поршня. 3) Какое количество Q теплоты подвели к воздуху в цилиндре в процессе нагревания к тому моменту, когда поршень начал смещаться?

2. Теплоизолированный цилиндр объемом V разделен на две части перегородкой. В одной части находится водород в количестве ν при температуре T₁, а в другой – азот в количестве 1,5ν при температуре 5/4 T₁ и другом давлении. Перегородка прорывается. 1) Какая температура T₂, установится в смеси? 2) Найти давление P в смеси.

3. В цилиндре с вертикальными гладкими стенками под покоящимся поршнем находятся вода и влажный воздух при температуре t₁ 100 °С. Площадь поршня S 100 см² , масса M поршня такова, что Mg0,5 P₀ S , здесь P₀1,010⁵ Па – давление в окружающей атмосфере. Высота поршня над поверхностью воды H 20 см. Температуру в цилиндре медленно уменьшили до t₂ 7 °С. Давление водяного пара при t₂ 7 °С считайте пренебрежимо малым. Универсальная газовая постоянная R 8,31 Дж/(моль∙K). Молярная масса воды ₁ 18 10^3 кг/моль. 1) Найдите парциальное давление P_СВ сухого воздуха в цилиндре под поршнем при t₁  100°С. 2) На каком расстоянии h от поверхности воды остановится поршень при t₂7 °С?

4. В цилиндрическом сосуде под поршнем находится насыщенный водяной пар при температуре 95 ⁰С и давлении P 8,5 10 ⁴ Па. В медленном изотермическом процессе уменьшения объема пар начинает конденсироваться, превращаясь в воду. 1) Найти отношение плотности пара к плотности воды в условиях опыта. 2) Найти отношение объема пара к объему воды к моменту, когда объем пара уменьшится в  4, 7 раза. Плотность и молярная масса воды 1 г/см³ ,  18 г/моль.

5. Водяной пар массой 3 г изотермически сжимают при температуре 81⁰С. Объем пара уменьшился в 3,5 раза, а давление возросло в 1,8 раза. Давление насыщенного водяного пара при 81 ⁰С равно 0,5^. 10⁵ Па. Пар считать идеальным газом. Молярная масса пара  18г/моль. Универсальная газовая постоянная R=8,31 Дж/(моль.К). 1) Найти начальное давление пара. 2) Найти конечный объем пара.

6. У идеального одноатомного газа в некотором процессе давление увеличилось на 2%, а объем уменьшился на 1%. В этом процессе относительные изменения давления, объема и температуры считать намного меньше единицы. 1) Как и на сколько процентов изменилась температура газа? 2) Найти в этом процессе отношение полученной газом теплоты к работе газа.

прошлые годы 11 класс

1 . На шероховатой горизонтальной поверхности стола находится доска. На гладкой верхней горизонтальной поверхности доски находится брусок, прикреплённый к доске лёгкой упругой пружиной (см. рисунок). Брусок отклоняют влево так, что пружина сжата на величину x, а доска прижата к упору. Затем брусок отпускают. 1) Найдите деформацию пружины в момент отрыва доски от упора. 2) Найдите скорость бруска в момент отрыва доски от упора. Известно следующее. Если брусок подвесить на пружине, то деформация пружины равна 4x/11. Если брусок с доской двигать по столу с постоянной скоростью, прикладывая горизонтальную силу к бруску, то деформация растянутой пружины равна 5x/6.

2. В цилиндре под поршнем находятся в равновесии ν молей воды (жидкость) и водяной пар при температуре T. При изобарическом нагревании цилиндра объём увеличивается в 4 раза, а температура — на 25%. Найдите работу, совершённую содержимым цилиндра в этом процессе. Объём жидкости намного меньше объёма пара. Пар считать идеальным газом.

1 . По гладкой горизонтальной поверхности стола движется со скоростью u горка с неподвижной относительно горки шайбой на нижнем горизонтальном участке горки (см. рисунок). Пуля, летящая горизонтально со скоростью 69u, попадает в шайбу и застревает в ней. В результате шайба заезжает на верхний горизонтальный участок горки, не отрываясь от её гладкой поверхности, и покидает горку. Массы пули и шайбы равны m и 6m, масса горки намного больше массы шайбы. 1) Найдите скорость шайбы v₁ относительно горки сразу после попадания пули. 2) Найдите скорость шайбы v₂ относительно стола сразу после попадания пули. 3) С какой скоростью относительно стола шайба покинула горку? Направления всех движений находятся в одной вертикальной плоскости. Известно, что при съезде изначально неподвижной шайбы с верхнего участка неподвижной горки на её нижний участок шайба приобретает скорость 6u.

2 . Идеальный газ совершает цикл, состоящий из адиабатического расширения, изотермического сжатия и изохорического нагревания, КПД которого равен η. 1) Во сколько раз работа газа при расширении больше работы над газом при сжатии? 2) Найдите отношение работы над газом при сжатии к работе газа за цикл.

1. В сосуде с водой закреплён клин. На гладкой поверхности клина, наклонённой к горизонту под углом α (tg α = 1/4), удерживается стеклянный шар с помощью горизонтально натянутой нити (см. рисунок). Объём шара V , плотность воды ρ, плотность стекла 3ρ. 1) Найдите силу натяжения нити при неподвижном сосуде. 2) Найдите силу натяжения нити при движении сосуда с горизонтальным ускорением a = g/8. В обоих случаях шар находится полностью в воде.

2. U-образная трубка с открытыми в атмосферу вертикальными коленами заполнена частично ртутью. Одно из колен закрывают сверху, а в другое доливают столько ртути, что после установления равновесия смещения уровней ртути в коленах (относительно начального положения) отличаются в 4 раза, а в закрытом колене остаётся слой воздуха длиной L = 25 см. Найдите атмосферное давление. Ответ выразить в миллиметрах ртутного столба (мм рт. ст.).

2 . Неподвижная теплопроводящая перегородка A делит объём теплоизолированного цилиндра на два отсека, в которых находится по ν моль гелия. Во втором отсеке газ удерживается подвижным теплоизолированным поршнем B. Наружное атмосферное давление равно p₀. В начальном состоянии температура гелия в первом отсеке больше, чем во втором. В результате медленного процесса теплообмена через перегородку температура в отсеках начинает выравниваться, а поршень перемещается. По окончании процесса теплообмена объём гелия во втором отсеке увеличивается на ∆V . Трением поршня о цилиндр, теплоёмкостью стенок цилиндра и поршня пренебречь. 1) Найдите отношение модулей изменения температуры в первом и втором отсеках после окончания теплообмена. 2) Найдите изменение температуры в первом отсеке.

1 . Массивная плита движется с постоянной скоростью U вертикально вверх. К плите подлетает шарик, имеющий перед ударом скорость V₁ = 8 м/с, направленную под углом α (sin α = 3/4) к вертикали (см. рис.). После неупругого удара о гладкую горизонтальную поверхность плиты шарик отскакивает со скоростью V₂, составляющей угол β (sin β = 1/2) с вертикалью. 1. Найти скорость V₂. 2. Найти возможные значения скорости плиты U при таком неупругом ударе. Действие силы тяжести за малое время удара не учитывать. Ответы допустимы через радикалы из целых чисел.

2 . Цилиндрический теплоизолированный горизонтально расположенный сосуд разделен на два отсека теплопроводящим поршнем, который может перемещаться горизонтально без трения. В первом отсеке находится азот, во втором — кислород, каждый газ в количестве ν = 3/7 моль. Начальная температура азота T₁ = 300 К, а кислорода T₂ = 500 К. Температуры газов начинают медленно выравниваться, а поршень начинает медленно двигаться. Газы считать идеальными с молярной теплоемкостью при постоянном объеме C_V = 5R/2. R = 8,31 Дж/(моль · К). 1. Найти отношение начальных объемов азота и кислорода. 2. Найти установившуюся температуру в сосуде. 3. Какое количество теплоты передал кислород азоту?

1. Груз массой m подтягивается по гладкой горизонтальной поверхности к стене с помощью лебедки, неподвижного небольшого легкого блока и легкого троса (см. рис.). Трос вытягивается лебедкой с постоянной скоростью V₀. Груз последовательно проходит точки 1, 2 и 3, для которых sin α₁ = 1/3, sin α₂ = 1/2, sin α₃ = 3/4. От точки 1 до точки 2 груз перемещается за время t₁₂. 1. Найти скорость V₁ груза при прохождении точки 1. 2. Найти работу лебедки A₁₂ при перемещении груза из точки 1 в точку 2. 3. Найти время t₂₃ перемещения груза из точки 2 в точку 3.

2. Цилиндрический сосуд, стоящий на горизонтальном столике, помещен в термостат, в котором поддерживается постоянная температура T₀ = 373 К. Стенки сосуда проводят тепло. Сосуд разделен на две части подвижным (нет трения при перемещении) поршнем. В нижней части находится воздух объемом V₁, в верхней — водяной пар и немного воды. Содержимое сосуда в равновесии. Поршень своим весом создает добавочное давление P₀/5, где P₀ — нормальное атмосферное давление. Сосуд переворачивают и ставят на столик, в верхней части оказывается воздух. Через некоторое время устанавливается новое равновесное состояние. 1. Найти объем V₂ воздуха в сосуде после переворачивания. 2. Найти изменение массы ∆m воды. 3. Найти изменение внутренней энергии содержимого сосуда. Удельная теплота испарения воды L, молярная масса воды µ. Массой воды, пара и воздуха по сравнению с массой поршня пренебречь. Объёмом воды при конденсации пара можно пренебречь по сравнению с объёмом пара, из которого образовалась вода. Воздух считать идеальным газом.

1 . Клин находится на горизонтальной поверхности стола. Лёгкая нерастяжимая нить, перекинутая через укреплённый на клине лёгкий блок, привязана к небольшому по размерам шару и стене (см. рис.). Систему удерживают в покое, отведя шар в сторону так, что нить составляет угол α (cos α = 3/5) с горизонтом, участок нити CA горизонтален, шар находится на расстоянии H от стола. Затем систему отпускают, она движется, при этом угол α наклона нити к горизонту не изменяется. 1. Под каким углом к горизонту направлено ускорение шара? Найти значение любой тригонометрической функции этого угла. 2. Найти ускорение клина. Ответ выразить через ускорение свободного падения g. 3. Найти отношение массы шара к массе клина. 4. Через какое время шар достигнет стола? Трением в системе пренебречь. Все точки системы перемещаются в вертикальной плоскости. Клин не переворачивается. Шар достигает стола раньше, чем клин доезжает до стены.

2 . Гелий в количестве ν моль охлаждается от начальной температуры T₀ в процессе с молярной теплоёмкостью, зависящей от температуры T линейно: C(T) = 2R . Здесь R — универсальная газовая постоянная. Гелий считать идеальным газом. 1. Какое количество теплоты Q₁ (Q₁ 0) отдаст газ в таком процессе при уменьшении температуры от T₀ до T₀? 2. До какой температуры надо охладить газ, чтобы газ совершил минимальную работу? 3. Найти эту минимальную работу.

2. С идеальным одноатомным газом проводят циклический процесс. Расширение газа (см. рис.) можно описать графиком в виде дуги окружности 1 − 2 с центром в начале координат на pV - диаграмме (p₀ и V₀ — некоторые фиксированные давление и объём). Неравновесное сжатие газа 2−1 характеризуется пренебрежимо малым теплообменом с окружающей средой. Радиусы, проведённые в точки 1 и 2, составляют углы 30^◦ и 15^◦ с осями p/p₀ и V/V₀ соответственно. 1. Найти отношение температур в состояниях 1 и 2. 2. Найти угол с горизонтальной осью, который составляет радиус, проведённый в точку с теплоёмкостью равной нулю в процессе расширения 1 − 2, если такая существует. Дать значение любой тригонометрической функции угла. 3. Найти отношение работы газа за цикл к работе газа при расширении. Ответы можно представить в виде числового выражения, не производя окончательного расчёта «до числа».

1 . Клин с углом наклона α (cos α = 12/13) находится на горизонтальном столе. Через невесомый блок, укреплённый на клине, перекинута лёгкая нерастяжимая нить, к концам которой привязаны шарик массой m и брусок массой 13m (см. рис.). Вначале систему удерживают неподвижно, расположив шарик вблизи блока на расстоянии H от стола, нить при этом не провисает. Затем клин стали двигать с постоянным горизонтальным ускорением, а шарик отпустили. Брусок и шарик пришли в движение, при этом нить, привязанная к шарику, составила угол β (cos β = 4/5) с вертикалью. Все точки системы перемещаются в вертикальной плоскости. Трением в оси блока и бруска о клин пренебречь. Шарик достигает стола раньше, чем брусок доезжает до блока. 1. Найти ускорение клина. 2. С каким ускорением относительно клина движется брусок? 3. Через какое время шарик достигнет стола?

3 . Две бесконечные плоские прямоугольные пластины AB и BC перпендикулярны друг к другу и образуют двугранный угол с ребром B. На рисунке показано сечение угла плоскостью, перпендикулярной ребру B. 1. Пластина BC заряжена с постоянной поверхностной плотностью заряда. Угол α = π/4. Во сколько раз увеличится напряженность электрического поля в точке K на середине отрезка AC, если пластину AB тоже зарядить с такой же поверхностной плотностью заряда? 2. Пластины BC и AB заряжены положительно с поверхностной плотностью заряда σ₁ = 2σ, σ₂ = σ, соответственно. Угол α = π/7. Найти напряженность электрического поля в точке K на середине отрезка AC.

3 . Два тонкостенных полых проводящих шара (тонкостенные сферы) с общим центром и радиусами r₁ и r₂ образуют сферический конденсатор (см. рис.). На внешнем шаре находится положительный заряд Q, внутренний шар не заряжен и соединен с Землей через ключ K и резистор R. Ключ замыкают. 1. Найти заряд q внутреннего шара после замыкания ключа. 2. Найти энергию W₀ электрического поля вне шаров до замыкания ключа. 3. Какое количество теплоты W выделится в резисторе R после замыкания ключа? Сопротивление проводов, шаров и Земли не учитывать. Радиусы шаров значительно меньше расстояния между Землей и шарами.

1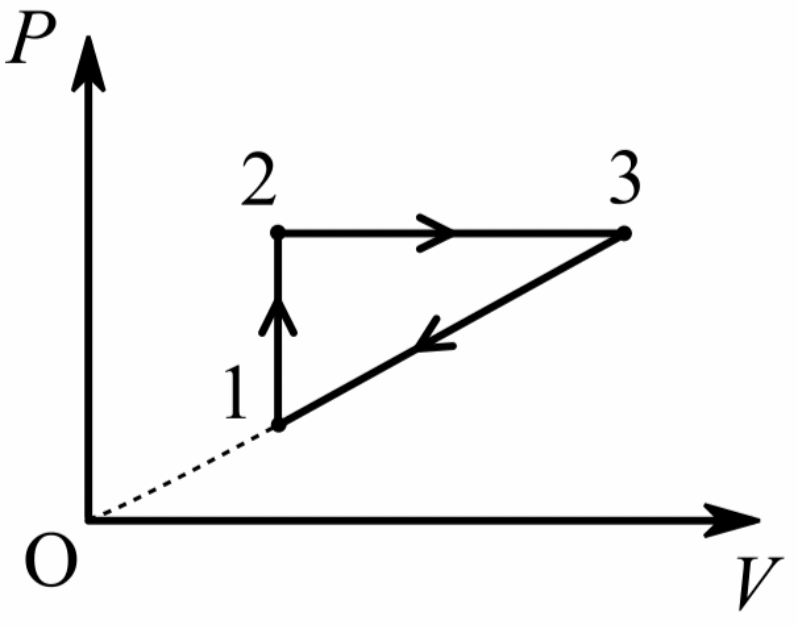 . Муфту M двигают со скоростью V = 68 см/с по горизонтальной направляющей AB (см. рис.). Кольцо K массой m = 0,1 кг, может двигаться без трения по проволоке CD в виде дуги окружности радиусом R = 1,9 м. Кольцо и муфта связаны лёгкой нитью длиной l = . Система находится в одной горизонтальной плоскости. В некоторый момент нить составляет угол α (cos α = 15/17) с направлением движения муфты и угол β (cos β = 4/5) с направлением движения кольца. 1. Найти скорость кольца в этот момент. 2. Найти скорость кольца относительно муфты в этот момент. 3. Найти силу натяжения нити в этот момент.

2. Тепловая машина работает по циклу, состоящему из изохоры, изобары и участка прямо пропорциональной зависимости давления P от объема V (см. рис.). Рабочее вещество — одноатомный идеальный газ. 1. Найти отношение молярных теплоемкостей на тех участках цикла, где происходило повышение температуры газа. 2. Найти в изобарном процессе отношение количества теплоты, полученной газом, к работе газа. 3. Найти предельно возможное максимальное значение КПД такого цикла.

3. Обкладки конденсатора — круглые металлические сетки площадью S, расстояние между обкладками d ( d « ) . Из точки, находящейся между обкладками на оси симметрии на расстоянии 0,25d от положительно заряженной обкладки, стартует с нулевой начальной скоростью положительно заряженная частица и через время T вылетает из конденсатора перпендикулярно обкладкам. Удельный заряд частицы = γ. Система находится в вакууме. 1. Найдите скорость V₁ частицы при вылете из конденсатора. 2. Найдите величину Q заряда обкладок конденсатора. 3. С какой скоростью V₂ будет двигаться частица на бесконечно большом расстоянии от конденсатора? При движении частицы электрическое поле, созданное зарядами конденсатора, считать неизменным, а электрическое поле внутри конденсатора вблизи оси симметрии считать однородным.

1 . Шарик подвешен в поле тяжести на легкой упругой пружине с неизвестной жесткостью. Шарик поднимают вверх до положения, когда пружина не деформирована, и отпускают. При дальнейшем движении шарика вдоль вертикали в некоторые моменты времени силы, действующие на шарик со стороны пружины, отличаются в 2 раза, а модули ускорений равны. 1. Найти модуль ускорения в эти моменты. 2. Найти отношение кинетических энергий шарика в эти моменты. 3. Найти отношение максимальной энергии деформации пружины к максимальной кинетической энергии шарика

2. Идеальный одноатомный газ из состояния 1 с температурой T₁ расширяется в процессе 1−2 прямо пропорциональной зависимости давления P от объема V . В процессе 1−2 давление увеличивается в k = 2 раза. Затем газ расширяется в изотермическом процессе 2 − 3, сжимается в процессе 3 − 4 прямо пропорциональной зависимости давления от объема и сжимается в изотермическом процессе 4 − 1. Объемы газа в состояниях 2 и 4 равны. 1. Найти температуру газа в процессе 2 − 3. 2. Найти отношение давлений в состояниях 1 и 3. 3. Найти молярную теплоемкость газа в процессе 1 − 2.

3. В электрической цепи (см. рис.) все элементы идеальные, конденсатор не заряжен. Величины E, R, C известны, r = R. Ключ K на некоторое время замыкают, а затем размыкают, когда скорость роста энергии конденсатора максимальна. 1. Найти ток, текущий через конденсатор, сразу после замыкания ключа. 2. Найти ток, текущий через конденсатор, сразу после размыкания ключа. 3. Какое количество теплоты выделится в цепи после размыкания ключа?

4. В цепи используется мостовая схема (см. рис.). ЭДС идеального источника E = 10 В, R₂ = 12 Ом, R₃ = 8 Ом, R₄ = 2 Ом. Вольтамперная характеристика диода показана на рисунке, пороговое напряжение диода U₀ = 1 В. 1. Найти ток через резистор R₃ при разомкнутом ключе K. 2. При каких значениях R₁ ток потечет через диод при замкнутом ключе K? 3. При каком значении R₁ мощность тепловых потерь на диоде будет равна P_D = 1,25 Вт?

1 . На гладкой горизонтальной поверхности стола покоится клин. Гладкая наклонная поверхность клина образует с горизонтом угол α такой, что cos α = 0,6. Если шайбе, находящейся у основания клина, сообщить начальную скорость V₀ вдоль поверхности клина (см. рис.), то к моменту достижения шайбой высшей точки траектории скорость шайбы уменьшается в n = 5 раз. В процессе движения шайба безотрывно скользит по клину, а клин по столу. Ускорение свободного падения g. Известными считать V₀, n и α. 1. Найдите отношение m/M массы шайбы к массе клина. 2. На какую максимальную высоту H, отсчитанную от точки старта, поднимается шайба в процессе движения по клину? 3. Через какое время T после старта шайба поднимается на максимальную высоту?