Методическое пособие по изучению
темы «Кодирование числовой информации»
«Информатика»
Оглавление
Аннотация ………………………………………………………….. 3
Введение ……………………………………………………………. 4
Содержание …………………………………………………………..
- Теоретическая часть.....………………………………………. 5
- Представление информации в ЭВМ………………………… 5
- Системы счисления, используемые при работе с ЭВМ…… 6
- Перевод чисел из одной системы счисления в другую……. 7
- Практические задания................................................................ 22
- Карточки для устных ответов ....................................................24
- Творческое задание …………………………………………... 25
- Эталоны ответов......................................................................... 26
4. Используемые источники …………………………………………… 28
Теоретическая часть
Представление информации в ЭВМ
Наиболее удобным средством представления информации, с точки зрения автоматизации процессов ее обработки, является язык чисел. Любой язык чисел определяется системой счисления.
Система счисления – способ наименования и изображения чисел с помощью символов, имеющих определенные количественные значения. Различают непозиционные и позиционные системы счисления. В непозиционной системе счисления цифры не меняют своего количественного значения при изменении их расположения в числе (например, римская система счисления). Тем самым исключается всякая возможность автоматизации распознавания чисел и, как следствие, обработки информации. Этого недостатка лишена позиционная система счисления, в которой значение каждой цифры зависит от ее места (позиции) в числе.
Позиционные системы счисления характеризуются:
основанием Р системы счисления – количеством (Р) различных символов, используемых для изображения чисел. Значения этих символов лежат в пределах от 0 до Р-1;
разрядом – позицией, занимаемой отдельным символом в изображении числа. Разряды нумеруются справа налево, начиная с 0;
весом разряда – количественным значением одной единицы разряда.
Любое число C в позиционной системе счисления с основанием Р может быть представлено в виде полинома:

 C= Cm Pm +Cm-1 Pm-1 +…+C1 P1 +C0 P0 +C-1 P-1 + C-2 P-2 +…+C-s P-s ,
C= Cm Pm +Cm-1 Pm-1 +…+C1 P1 +C0 P0 +C-1 P-1 + C-2 P-2 +…+C-s P-s ,
целая часть числа дробная часть числа
или где в качестве Ci могут стоять любые из Р цифр алфавита, а нижние индексы определяют местоположение цифры в числе (разряд)
Численно вес разряда определяется через основание Р системы счисления и номер i разряда: Рi. Таким образом, максимальное целое число, которое может быть представлено в m разрядах Nmax = Pm -1.
Минимальное значащее (не равное 0) число, которое можно записать в s разрядах дробной части Nmin = P-s. Тогда, имея в целой части числа m, а в дробной s разрядов, можно представить Pm+s чисел от 0 до Pm+s-1.
Поскольку в технике известно много физических приборов и сред с двумя устойчивыми состояниями, в качестве алфавита языка ЭВМ приняты символы 0 и 1, названные двоичными цифрами. Последовательности нулей и единиц конечной длины образуют двоичные числа, которые, в свою очередь, образуют позиционную двоичную систему счисления.
Системы счисления, используемые при работе с ЭВМ.
В вычислительной технике применяют позиционные системы счисления с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную и др. Для обозначения используемой системы счисления числа заключают в скобки и индексом указывают основание системы счисления: 15(10), 1011(2) ,735(8) , 1EA9F(16). Иногда скобки опускают и оставляют только индекс: 1510, 10112 ,7358 , 1EA9F16. Есть еще один способ обозначения системы счисления: при помощи латинских букв добавляемых после числа. Например, 15 D; 1011 В; 735 Q; 1EA9F H.
Двоичная система счисления. Основание Р=2. Алфавит включает две двоичные цифры: 0, 1. Веса разрядов в двоичной системе счисления равны 1, 4, 8, 16,... влево от запятой и 0,5; 0,25; 0,125; 0,625;... вправо от запятой.
Двоичная система счисления имеет ряд преимуществ перед другими системами:
для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток — нет тока, намагничен — не намагничен и т.п.);
представление информации посредством только двух состояний надежно и помехоустойчиво;
возможно применение аппарата булевой алгебры для выполнения логических преобразований информации;
двоичная арифметика намного проще десятичной.
Недостаток двоичной системы — быстрый рост числа разрядов, необходимых для записи чисел.
Таблица 1
| десятичные | двоичные | восьмеричные | шестнадцатеричные |
| 0 | 0000 | 0 | 0 |
| 1 | 0001 | 1 | 1 |
| 2 | 0010 | 2 | 2 |
| 3 | 0011 | 3 | 3 |
| 4 | 0100 | 4 | 4 |
| 5 | 0101 | 5 | 5 |
| 6 | 0110 | 6 | 6 |
| 7 | 0111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
Восьмеричная и шестнадцатеричная системы счисления используются при составлении программ на языке машинных кодов для более короткой и удобной записи двоичных кодов — команд, данных, адресов и операндов. Алфавит восьмеричной системы счисления включает цифры от 0 до 7. Алфавит шестнадцатеричной системы счисления включает цифры от 0 до 9, для изображения цифр, больших 9, применяются латинские буквы A, B, C, D, E, F. 1. Двоично-десятичная система счисления получила большое распространение в современных ЭВМ ввиду легкости перевода в десятичную систему и обратно. Она используется там, где основное внимание уделяется не простоте технического построения машины, а удобству работы пользователя. В этой системе счисления все десятичные цифры отдельно кодируются четырьмя двоичными цифрами.
Примеры.
Десятичное число 9703 в двоично-десятичной системе выглядит так:
1001 0111 0000 00112.
Десятичное число 6251 в двоично-десятичной системе выглядит так:
0 0101 00012.
Перевод чисел из одной системы счисления в другую.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
(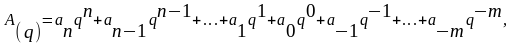 1)
1)
При переводе удобно пользоваться таблицами степеней:
Степени числа 2
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 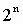
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Степени числа 8
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 
| 1 | 8 | 64 | 512 | 4096 | 32768 | 262144 |
Степени числа 16
| n (степень) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 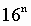
| 1 | 16 | 256 | 4096 | 65536 | 1048576 | 16777216 |
Пример 1. Перевести число 1011101.001 из двоичной системы счисления (СС) в десятичную СС.
Решение:
1011101.0012 =1·26+0·25+1·24+1·23+1·22 +0·21+1·20+0·2-1+0·2-2+1·2-3 =64+16+8+4+1+1/8=93.12510
Пример 2. Перевести число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС.
Решение:
Пример 3. Перевести число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС.
Решение:
Здесь A -заменен на 10, B - на 11, C- на 12, F - на 15.
Пример 4:
1) 10000012 = 1 × 26 + 0 × 25 + 0 × 24 + 0 × 23 + 0 × 22 + 0 × 21 + 1 × 20 = 64 + 1 = 6510
Замечание. Если в каком-либо разряде стоит нуль, то соответствующее слагаемое можно опускать.
2) 1000011111,01012 = 1 × 29 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 + 1 × 2–2 + 1 × 2–4 = 512 + 16 + 8 + 4 + 2 + 1 + 0,25 + 0,0625 = 543,312510
3) 1216,048= 1 × 83 + 2 × 82 + 1 × 81 + 6 × 80 + 4 × 8–2 = 512 + 128 + 8 + 6 + 0,0625 = =654,062510
4) 29A,516 = 2 × 162 + 9 × 161 + 10 × 160 + 5 × 16–1 = 512 + 144 + 10 + 0,3125 =656,312510
Перевод чисел из десятичной системы счисления в другую систему счисления
Алгоритм перевода из десятичной системы в двоичную
Выполнить деление исходного числа на 2. Если результат деления больше или равен 2, продолжать делить его на 2 до тех пор, пока результат деления не станет равен 1.
Выписать результат последнего деления и все остатки от деления в обратном порядке в одну строку.
Пример 4. Перевести число 159 из десятичной СС в двоичную СС:
| 159 | 2 | | | | | | |
| 158 | 79 | 2 | | | | | |
| 1 | 78 | 39 | 2 | | | | |
| | 1 | 38 | 19 | 2 | | | |
| | | 1 | 18 | 9 | 2 | | |
| | | | 1 | 8 | 4 | 2 | |
| | | | | 1 | 4 | 2 | 2 |
| | | | | | 0 | 2 | 1 |
| | | | | | | 0 | |
Ответ: 15910=100111112.
Алгоритм перевода чисел из десятичной системы в восьмеричную
Разделить исходное число на 8. Найти максимальное частное и убрать дробную часть от него. Например, исходное число 20 : 8 = 2,5. Значит, в частное мы записываем число 2.
Умножить полученное частное на 8. Записать его под исходным числом.
Найти остаток между этими числами и выделить его – это кусочек переведённого в восьмеричную систему числа.
Затем разделить в столбик полученное частное на 8, записать ответ и проделать шаги 2 и 3.
Производить деление до тех пор, пока делимое не станет меньше 8. Выделить это делимое тоже.
Выписать все выделенные числа справа налево (т.е. последнее делимое будет на первом месте, затем идёт остаток, найденный на последнем шаге, затем остаток, найденный на предпоследнем шаге и т.д.). Полученное при такой записи число и будет искомым восьмеричным.
Пример 5. Перевести число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | | |
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| | 4 | 8 | 1 |
| | | 1 | |
Ответ: 61510=11478.
Пример 6. Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | | |
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| | 13 | 64 | 4 |
| | | 12 | |
Как видно из рисунка последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 - D. Следовательно наше шестнадцатеричное число - это 4CD9.
Ответ: 1967310=4CD9.
Примеры:
4687710 переводим в шестнадцатиричную систему счисления:
46877 / 16 = 2929 - остаток 13 = D
2929 / 16 = 183 - остаток 1
183 / 16 = 11 - остаток 7
11 = B
Записав цифры всех остатков в обратном порядке, получим число B71D16
Таким образом 4687710 = B71D16
2) 204710 переводим в шестнадцатиричную систему счисления:
2047 / 16 = 127 - остаток 15 - F
127 / 16 = 7 - остаток 15 - F
7
Записав цифры всех остатков в обратном порядке, получим число 7FF16
Таким образом 204710 = 7FF16
3) 76710 переводим в шестнадцатиричную систему счисления:
767 / 16 = 47 - остаток 15 = F
47 / 16 = 2 - остаток 15 = F
2
Записав цифры всех остатков в обратном порядке, получим число 2FF16
Таким образом 76710 = 2FF16
4) 48510 переводим в шестнадцатиричную систему счисления:
485 / 16 = 30 - остаток 5
30 / 16 = 1 - остаток 14 = E
1
Записав цифры всех остатков в обратном порядке, получим число 1E516
Таким образом 48510 = 1E516
5)18010 переводим в шестнадцатиричную систему счисления:
180 / 16 = 11 - остаток 4
11 = b
Записав цифры всех остатков в обратном порядке, получим число b416
Таким образом 18010 = b416
6) 12710 переводим в шестнадцатиричную систему счисления:
127 / 16 = 7 - остаток 15 = F
7
Записав цифры всех остатков в обратном порядке, получим число 7F16
Таким образом 12710 = 7F16
7) 8710 переводим в шестнадцатиричную систему счисления:
87 / 16 = 5 - остаток 7
5
Записав цифры всех остатков в обратном порядке, получим число 5716
Таким образом 8710 = 5716
8) 7010 переводим в шестнадцатиричную систему счисления:
70 / 16 = 4 - остаток 6
4
Записав цифры всех остатков в обратном порядке, получим число 4616
Таким образом 7010 = 4616
9) 3210 переводим в шестнадцатиричную систему счисления:
32 / 16 = 2 - остаток 0
2
Записав цифры всех остатков в обратном порядке, получим число 2016
Таким образом 3210 = 2016
Результат: 62210= 26E16
Перевод десятичной дроби в любую другую позиционную систему счисления
Алгоритм перевода правильных десятичных дробей в любую СС
Для того, чтобы выполнить перевод правильных дробей из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную необходимо последовательно умножать правильную дробь и получаемые дробные части произведений на основание системы q до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа.
Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.
Пример 1: Переведем правильную десятичную дробь 0,875 в двоичную систему
счисления
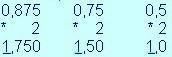
Процесс умножения закончен, т.к. получена нулевая дробная часть. Последовательность целых частей, выписанных в порядке получения, является дробной частью числа в двоичной системе счисления. Целая часть двоичной дроби равна нулю. Итак, 0,87510=0,1112.
Пример 2: Перевести десятичное число 0,25 в двоичную систему счисления
0,2510=0,012
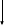 0,25 · 2 = 0,5;
0,25 · 2 = 0,5;
0,5· 2 = 1,0
Пример 3: Перевести десятичное число 0,53 в двоичную систему счисления с точностью до шестого знака после запятой.
0,5310 = 0,1000012
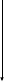 0,53 · 2 = 1,06;
0,53 · 2 = 1,06;
0,06 · 2 = 0,12
0,12 · 2 = 0,24
0,24 · 2 = 0,48
0,48 · 2 = 0,96
0,96 · 2 = 1,92
Пример 4:
0,3510 = 0,010112
0,562510=0,10012
0,84710=0,11012
Пример 5: Перевести десятичное число 0,13 в восьмеричную систему счисления с точностью до шестого знака после запятой.
0,1310 =0,1024368
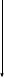
0,13 · 8 = 1,04
0,04 · 8 = 0,32
0,32 · 8 = 2,56
0,56 · 8 = 4,48
0,48 · 8 = 3,84
0,84 · 8 = 6,72
Пример 6: Перевести десятичное число 0,96 в восьмеричную систему счисления с точностью до пятого знака после запятой.
0,9610 = 0,753418
0,96 · 8 = 7,68
0,68 · 8 = 5,44
0,44 · 8 = 3,52
0,52 · 8 = 4,16
0,16 · 8 = 1,28
Пример 7:
0,3510 = 0,2638
0,6562510=0,528
Пример 8: Перевести десятичное число 0,891 в шестнадцатеричную систему счисления с точностью до пятого знака после запятой.
0,89110 = 0,Е418916
0,891 · 16 = 14,256
0,256 · 16 = 4,096
0,096 · 16 = 1,536
0,536 · 16 = 8,576
0,576 · 16 = 9,216
Пример 9: Перевести десятичное число 0,398 в шестнадцатеричную систему счисления с точностью до четвёртого знака после запятой.
0,39810 = 0,65Е3
0,398 · 16 = 6,368
0,368 · 16 = 5,888
0,888 · 16 = 14,208
0,208 · 16 = 3,328
Алгоритм перевода смешанных десятичных дробей в любую СС
Перевод смешанных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Пример 1: Перевести десятичное число 13,25 в двоичную систему счисления.
13,2510 = 1101,012
| 13 | 2 |
|
|
| 12 | 6 | 2 |
|
| 1 | 6 | 3 | 2 |
|
| 0 |  2 2
| 1 |
|
|
| 1 |
|
 0,25 · 2 = 0,5;
0,25 · 2 = 0,5;
0,5· 2 = 1,0
Пример 2: Перевести десятичное число 42,33 в восьмеричную систему счисления с точностью до двух знаков после запятой.
42,3310 = 52,258
| 42 | 8 |
| 40 | 5 |
|  2 2
|
|
|
|
|
|
|
|
0,33 · 8 =
2,64
0,64 · 8 = 5,12
Пример 3: Перевести десятичное число 425,77 в шестнадцатеричную систему счисления с точностью до трёх знаков после запятой.
425,7710 = 1А9,C5116

| 425 | 16 |
|
| 32 | 26 | 16 |
| 105 | 16 | 1 |
| 96 |  10 10
|
|
| 9 |
|
|
|
|
|
|
0,77 · 16 =
12,32
0,32 · 16 = 5,12
0,12 · 16 = 1,92
Пример 4: Сколько единиц в двоичной записи десятичного числа 14,125?
Соединим целую и дробную части:

Количество единиц равно 4.
Перевод чисел из двоичной системы счисления в восьмеричную
10100100010111011002= ?8 Для начала нам необходимо разбить это число на триады – группы из трёх цифр.
У систем счислений имеются основания. И у двоичной системы основание – 2. Нам необходимо перевести двоичное число в восьмеричную систему с основанием 8. Математически это можно записать так: 2i=8, i = 3, то есть, для записи одного восьмеричного числа в двоичной системе необходимо 3 бита или3 двоичные цифры. Поэтому мы и будем разбивать двоичное число на триады. Однако надо запомнить, что делать это надо начиная с конца.
Внимание: если старшая триада не заполнена, до конца, перед ней необходимо дописать столько нулей, чтобы получилась полноценная триада.
Теперь всё, что нам остаётся – это перевести каждую из этих триад из двоичной системы счисления в восьмеричную. Это можно сделать самостоятельно:
Затем, полученные результаты по каждой отдельной триаде надо выписать, начиная с самой первой. Записанное число и будет нашим конечным результатом в восьмеричной системой счисления.
Однако можно сильно облегчить себе задачу, не высчитывая все триады числа, а просто сверяя каждую из них по таблице соответствия двоичных чисел восьмеричным, например, по такой:
| Двоичная СС | Восьмеричная СС |
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Теперь можно просто смотреть на триаду, сверять её с таблицей и записывать число, соответствующее ей в восьмеричной системе.
Пример 1: Число 1011000010001100102 переведем в восьмеричную систему счисления.
 Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:
Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:
| 101 | 100 | 001 | 000 | 110 | 010 |
|  5 5
| 4 | 1 | 0 | 6 | 2 |
Получаем восьмеричное представление исходного числа: 5410628.
Замечание: Если число является дробным, то разбивка выполняется вправо и влево от разделителя целой и дробной части. Неполные крайние триады дописываются нулями.
Выполняется перевод отдельно для каждой триады, получившиеся символы записываются последовательно друг за другом.
Пример 1. Число 0,101100012 переведем в восьмеричную систему счисления.
Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:
|  0, 0,
| 101 | 100 | 010 |
| 0, | 5 | 4 | 2 |
Получаем восьмеричное представление исходного числа: 0,5428.
Пример 2:
Перевести двоичное число 10111001,011012 в восьмеричную систему счисления.


0 1 1 1 0 0 1 , 0 1 1 0 12 = 010 111 001 , 011 0102 = 271,328
Пример 3: Перевести двоичное число 1011000011,10012 в восьмеричную систему счисления.
1011000011,10012 = 001 011 000 011 , 100 1002 = 1303,448
Перевод чисел из двоичной системы счисления в шестнадцатеричную.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи. 16 = 2i . Так как 16 = 24, то i = 4 бита. Каждый разряд шестнадцатеричного числа содержит 4 бита информации. Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями. Затем надо преобразовать каждую группу в шестнадцатеричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия тетрад и шестнадцатеричных цифр.
Таблицы для перевода:
| Двоичная СС | Шестнадцатеричная СС | | 0000 | 0 | | 0001 | 1 | | 0010 | 2 | | 0011 | 3 | | 0100 | 4 | | 0101 | 5 | | 0110 | 6 | | 0111 | 7 | | 1000 | 8 | | 1001 | 9 | | 1010 | A | | 1011 | B | | 1100 | C | | 1101 | D | | 1110 | E | | 1111 | F |
|
Пример 1. Число 10000000001111100001112 переведем в шестнадцатеричную систему счисления.
Разбиваем число справа налево на тетрады (4 цифры) и под каждой из них записываем соответствующую шестнадцатеричную цифру:
| 0010 | 0000 | 0000 | 1111 | 1000 | 0111 |
| 2 | 0 | 0 | F | 8 | 7 |
Получаем шестнадцатеричное представление исходного числа: 200F8716.
Пример 2. Число 0,1000000000112 переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
| 0, | 1000 | 0000 | 0011 |
| 0, | 8 | 0 | 3 |
Получаем шестнадцатеричное представление исходного числа: 0,80316
Пример 3: Перевести двоичное число 111101,011012 в шестнадцатеричную систему счисления.
111101,011012 = 0011 1101 , 0110 10002 = 3D,6816
Пример 4: Перевести двоичное число 1010000,011102 в шестнадцатеричную систему счисления.
1010000,011102 = 0101 0000 , 0111 00002 = 50,716
Алгоритм перевода смешанных чисел.
Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой.
2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов;
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n
Перевод чисел из восьмеричной в двоичную систему счисления
Для перевода числа из восьмеричной в двоичную систему счисления достаточно перевести каждый символ отдельно, а затем записать символы последовательно друг за другом, причём, каждое двоичное число, соответствующее одному восьмеричному символу, должно состоять из трёх разрядов – триад (т.к. 8 = 23). Пустые позиции в начале числа заполняются нулями.
Внимание: Если в старших битах (то есть в самом начале двоичного числа) имеются нули, необходимо убрать их до первой единицы.
Пример 1: Перевести восьмеричное число 615,278 в двоичную систему счисления:
68 = 1102
18 = 0012
58 = 1012
28 = 0102
78 = 1112
615,278 = 110001101,0101112
Пример 2: Перевести восьмеричное число 173,548 в двоичную систему счисления
18 = 0012
78 = 1112
38 = 0112
58 = 1012
48 = 1002
173,548 = 1111011,1011002
Перевод чисел из шестнадцатеричной в двоичную систему счисления.
Для перевода числа из шестнадцатеричной в двоичную систему счисления достаточно перевести каждый символ отдельно, а затем записать символы последовательно друг за другом, причём, каждое двоичное число, соответствующее одному шестнадцатеричному символу, должно состоять из четырёх разрядов – тетрад (т.к. 16 = 24). Пустые позиции в начале числа заполняются нулями.
Пример 1: Перевести шестнадцатеричное число 6F3,A516 в двоичную систему счисления
616 = 01102
F16 = 11112
316 = 00112
A16 = 10102
516 = 01012
6F3,A516 = 11011110011,101001012
Пример 2: Перевести шестнадцатеричное число A39,F416 в двоичную систему счисления
A16 = 10102
316 = 00112
916 = 10012
F16 = 11112
416 = 01002
A39,F416 = 101000111001,111101002
Перевод чисел из восьмеричной в шестнадцатеричную систему счисления.
Перевод чисел из восьмеричной в шестнадцатеричную систему счисления удобно выполнять через двоичную систему счисления.
Для этого необходимо выполнить следующие действия:
Восьмеричное число перевести в двоичное число, причём, каждое двоичное число, соответствующее одному восьмеричному символу, должно состоять из триад;
Полученное двоичное перевести в шестнадцатеричную систему счисления, разбив двоичное число на тетрады.
Пример 1: Перевести восьмеричное число 534,7138 в шестнадцатеричную систему счисления.
534,7138 = 1 0 1 0 1 1 1 0 0 , 1 1 1 0 0 1 0 1 12 =
58 38 48 78 18 38
= 0001 0101 1100 , 1110 0101 10002 = 15С,Е5816
Пример 2: Перевести восьмеричное число 360,2348 в шестнадцатеричную систему счисления.
360,2348 = 0 1 1 1 1 0 0 0 0 , 0 1 0 0 1 1 1 0 02 =
38 68 08 28 38 48
= 0000 1111 0000 , 0100 1110 00002 == F0,4E16
Перевод чисел из шестнадцатеричной в восьмеричную систему счисления.
Перевод чисел из шестнадцатеричной в восьмеричную систему счисления удобно выполнять через двоичную систему счисления.
Для этого необходимо выполнить следующие действия:
Шестнадцатеричное число перевести в двоичное число, причём, каждое двоичное число, соответствующее одному шестнадцатеричному символу, должно состоять из тетрад.
Полученное двоичное перевести в восьмеричную систему счисления, разбив двоичное число на триады.
Пример 1: Перевести шестнадцатеричное число A2C,316 в восьмеричную систему счисления.
A2C,316 = 1 0 1 0 0 0 1 0 1 1 0 0 , 0 0 1 12 = 101 000 101 100 , 001 1002 =
A16 216 C16 316
= 5054,148
Пример 2: Перевести шестнадцатеричное число CBF5,E616 в восьмеричную систему счисления.
CBF5,E616 = 1 1 0 0 1 0 1 1 1 1 1 1 0 1 0 1 , 1 1 1 0 0 1 1 02 =
C16 B16 F16 516 E16 616
= 001 100 101 111 110 101, 111 001 1002 = 145765,71416
Практические задания
1) Запишите первые 20 целых чисел в троичной, пятеричной и восьмеричной системах счисления.
2) Какие целые числа следуют за числами:
|
а) 12;
|
е) 18;
|
п) F16;
|
|
б) 1012;
|
ж) 78;
|
м) 1F16;
|
|
в) 1112;
|
з) 378;
|
н) FF16;
|
|
г) 11112;
|
и) 1778;
|
о) 9AF916;
|
|
д) 1010112;
|
к) 77778;
|
п) CDEF16 ?
|
3) Какие целые числа предшествуют числам:
|
а) 102;
|
е) 108;
|
л) 1016;
|
|
б) 10102;
|
ж) 208;
|
м)2016;
|
|
в) 10002;
|
з) 1008;
|
н) 10016;
|
|
г) 100002;
|
и) 1108;
|
о) A1016;
|
|
д) 101002;
|
к) 10008;
|
п) 100016?
|
4) Какой цифрой заканчивается четное двоичное число? Какой цифрой
заканчивается нечетное двоичное число? Какими цифрами может заканчиваться четное троичное число?
5) Какое наибольшее десятичное число можно записать тремя цифрами:
а) в двоичной системе;
б) в восьмеричной системе;
в) в шестнадцатеричной системе?
6) В какой системе счисления справедливо следующее:
а) 20 + 25 = 100;
б) 22 + 44 = 110?
7) Десятичное число 59 эквивалентно числу 214 в некоторой другой системе счисления. Найдите основание этой системы.
8) Переведите числа в десятичную систему, а затем проверьте результаты, выполнив обратные переводы:
|
а) 10110112;
|
е) 5178;
|
л) 1F16;
|
|
б) 101101112;
|
ж) 10108;
|
м) ABC16;
|
|
в) 0111000012;
|
з) 12348;
|
н) 101016;
|
|
г) 0,10001102;
|
и) 0,348;
|
о) 0,А416;
|
|
д) 110100,112;
|
к) 123,418;
|
п) 1DE,C816.
|
9) Переведите числа из десятичной системы в двоичную, восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
а) 12510; б) 22910; в) 8810; г) 37,2510; д) 206,12510.
10) Переведите числа из двоичной системы в восьмеричную и шестнадцатеричную, а затем проверьте результаты, выполнив обратные переводы:
|
а) 1001111110111,01112;
|
г) 1011110011100,112;
|
|
б) 1110101011,10111012;
|
д) 10111,11111011112;
|
|
в) 10111001,1011001112;
|
е) 1100010101,110012.
|
11) Переведите в двоичную и восьмеричную системы шестнадцатеричные числа: а) 2СE16; б) 9F4016; в) ABCDE16; г) 1010,10116;
д) 1ABC,9D16.
12) Выпишите целые числа:
а) от 1011012 до 1100002 в двоичной системе;
б) от 2023 до 10003 в троичной системе;
в) от 148 до 208 в восьмеричной системе;
г) от 2816 до 3016 в шестнадцатеричной системе.
13) Для десятичных чисел 47 и 79 выполните цепочку переводов из одной системы счисления в другую:
Карточки для устных заданий
Карточка №1
Задание №1. Что такое по-вашему система счисления?
Задание №2. Какие системы счисления вы знаете?
Задание №3. В чем отличие арабской системы счисления от римской?
Задание №4. Как вы думаете, а есть другие системы счисления.
Карточка №2
Задание №1. Дайте определение понятиям:
Система счисления
Алфавит системы счисления
Основание системы счисления
Разряд
Задание №2. Объясните различие между позиционной и непозиционной системами счисления.
Задание №3. Число 71 в некоторой системе счисления с основание х записывается как 56х. Определите основание системы счисления.
Задание №4. Перечислите алфавит и назовите основание двоичной системы счисления.
Карточка №3
Задание №1. Расскажите алгоритм перевода числа из десятичной системы счисления в двоичную.
Задание №2. Расскажите алгоритм перевода числа из двоичной системы счисления в десятичную.
Задание №3. Расскажите алгоритм перевода чисел из двоичной системы счисления в восьмеричную при помощи триад.
Задание №4. Назовите числа которые не могут существовать в системе счисления с основанием 8: 325, 675, 482, 333, 191.
Творческое задание
а) Перевести числа из разных систем счисления в десятичную систему счисления и по полученным результатам на листочке построить график в системе координат. Затем придумать свое изображение и таблицу по нему.
| х | у |
| 10000(2) | 10(16) |
| D(16) | 20(8) |
| 1010(2) | 17(8) |
| 10(8) | 1111(2) |
| 110(2) | 11(16) |
| 5(16) | 10000(2) |
| 6(16) | 16(8) |
| 101(2) | 1100(2) |
| 6(8) | B(16) |
| 1000(2) | 15(8) |
| 14(8) | 1011(2) |
| 1101(2) | 11(8) |
| 1111(2) | 9(16) |
| 20(8) | 13(8) |
| 10010(2) | 1011(2) |
| 24(8) | D(16) |
| 13(16) | 1110(2) |
| 12(16) | F(16) |
| 10(16) | 20(8) |
| 17(8) | 10001(2) |
| 12(8) | 21(8) |
| 1001(2) | 1111(2) |
| х | у |
| 11(8) | 10000(2) |
| 12(8) | 15(8) |
| 110(2) | 10(8) |
| 6(16) | 111(2) |
| 1010(2) | 7(8) |
| 16(8) | А(16) |
| 10010(2) | 1011(2) |
| 24(8) | E(16) |
| 17(16) | 10000(2) |
| 30(8) | 12(16) |
| 10001(2) | 21(8) |
| 13(16) | 10101(2) |
| 22(8) | 1A(16) |
| 11(16) | 32(8) |
| 15(8) | 15(16) |
| D(16) | 17(10) |
| 13(8) | 10011(2) |
| 1010(2) | 23(8) |
| 1001(2) | 10010(2) |
| 11(8) | 10001(2) |
| 1000(2) | 21(8) |
| (16) | 10(16) |
Эталоны ответов
1) троичная: 0, 1, 2, 10, 11, 12, 20, 21, 22, 100, 101, 102, 110, 111, 112, 120, 121, 122, 200, 201; пятеричная: 0, 1, 2, 3, 4, 10, 11, 12, 13, 14, 20, 21, 22, 23, 24, 30, 31, 32, 33, 34.
2) а) 102; б) 1102; в) 10002; г) 100002; д) 1011002; е) 28; ж) 108; з) 408; и) 2008; к) 100008; л) 1016; м) 2016; н) 10016; о) 9AFA16; п) CDF016.
3) а) 12; б) 10012; в) 1112; г) 11112; д) 100112; е) 78; ж) 178; з) 778; и) 1078; к) 7778; л) F16; м) 1F16; н) FF16; о) A0F16; п) FFF16.
4) Четное двоичное число оканчивается цифрой 0, нечетное двоичное — цифрой 1, четное троичное — цифрами 0, 1 или 2.
5) а) 7; б) 511; в) 4091.
6) а) ни в какой; б) в шестеричной.
7) Основание 5.
8) а) 91; б) 183; в) 225; г) 35/64; д) 52,75; е) 335; ж) 520; з) 668; и) 7/16; к) 8333/64; л) 31; м) 2748; н) 4112; о) 41/64; п) 47825/32.
9) а) 11111012; 1758; 7D16; б) 111001012; 3458; E516; в) 10110002; 1308; 5816; г) 100101,012; 45,28; 25,416; д) 11001110,0012; 316,18; CE,216.
10) а) 11767,348; 13F7,716; б) 1653,5648; 3AB,BA16; в) 271,5478; B9,B3816; г) 13634,68; 179C,C16; д) 27,76748; 17,FBC16; е) 1425,628; 315,C816.
11) а) 10110011102; 13168; б) 10011111010000002; 1175008; в) 101010111100110111102; 25363368; г) 1000000010000,0001000000012; 10020,04018; д) 1101010111100,100111012; 15274,4728.
12) а) 1011012, 1011102, 1011112, 1100002; б) 2023, 2103, 2113, 2123, 2203, 2213, 2223, 10003; в) 148, 158, 168, 178, 208; г) 2816, 2916, 2A16, 2B16, 2C16, 2D16, 2E16, 2F16, 3016;
13) а) 4710-1011112-578-4710-578-1011112-2F16-4710-2F16-1011112-4710; б) 7910-10011112-1178-7910-1178-10011112-4F16-7910-4F16-10011112-7910.
Творческое задание
б)
Используемые источники:
1. Информатика : учебник / Н.Д. Угринович. — Москва : КноРус, 2018. — 377 с. — Для СПО.
Информатика. Практикум : практикум / Н.Д. Угринович. — Москва : КноРус, 2018.
Информатика (базовый курс) учебное пособие Р.С. Борисов, А.В. Лобан. — Электрон. текстовые данные. — М.: Российский государственный университет правосудия, 2014.
http://ru.wikipedia.org/wiki
Алексеев Е.Г., Богатырев С.Д. Информатика. Мультимедийный электронный учебник http://inf.e-alekseev.ru/text/Schisl_perevod.html
23








 C= Cm Pm +Cm-1 Pm-1 +…+C1 P1 +C0 P0 +C-1 P-1 + C-2 P-2 +…+C-s P-s ,
C= Cm Pm +Cm-1 Pm-1 +…+C1 P1 +C0 P0 +C-1 P-1 + C-2 P-2 +…+C-s P-s , 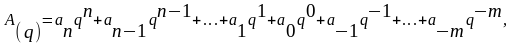 1)
1)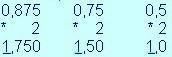
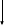 0,25 · 2 = 0,5;
0,25 · 2 = 0,5;  0,53 · 2 = 1,06;
0,53 · 2 = 1,06;
 2
2