КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«АЛТАЙСКИЙ КОЛЛЕДЖ ПРОМЫШЛЕННЫХ ТЕХНОЛОГИЙ И БИЗНЕСА»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ДЛЯ ОБУЧАЮЩИХСЯ ПРИ ИЗМЕРЕНИИ РАССТОЯНИЯ ПО КАРТЕ С ПОМОЩЬЮ ГЕОГРАФИЧЕСКИХ КООРДИНАТ

Бийск 2019
Рассмотрена на заседании ПЦК ТГС и ДПИ
Председатель ПЦК ТГС и ДПИ
Чекменева О.В __________
Ф.И.О. (подпись)
«____» _______________ 2019 г.
Составитель: преподаватель КГБПОУ «АКПТИБ» Кобызев Н.С.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Данное пособие разработано для студентов, обучающихся по профессии «Туризм», при освоении ПМ 02 «Предоставление услуг по сопровождению туристов», а также при организации спортивных походов на начальной стадии их подготовки, в том числе при работе с распечатанными картами неизвестных масштабов.
Пособие сможет наглядно продемонстрировать процесс вычисления расстояния по картам разного размера (в том числе с обрезанными географическими координатами), а именно:
1. Способы измерения расстояния по картам разного масштаба по географическим координатам;
2. Вычисление масштаба карты при увеличении карты на компьютере до карты более крупного масштаба;
1 Из истории измерения расстояний
В жизни неопытных туристов, путешествующих самостоятельно впервые, либо у молодых руководителей спортивно-туристских походов нередко возникает вопрос о происхождении координат на карте и поиску масштаба карты без наличия такового. На старых (40 – 60-х годов прошлого столетия) рассекреченных картах генштабов различных районов не только Алтая, но и всего нашего необъятного государства, практически никогда нет указанного масштаба на листах карт.
Из курса геодезии, картографии и топографии можно сильно удивиться, узнав, что истинные листы карты абсолютно не имеют квадратной формы. Листы карты имеют форму трапеции в силу деления глобуса земного шара на части (по принципу деления апельсина, если его разрезать на несколько равных долей сверху вниз).
Подобными изысканиями и вычислениями занимались древнегреческий историк Геродот, нидерландский картограф и географ Герард Меркатор, позднеэллинистический астроном, астролог, математик, механик, оптик, теоретик музыки и географ Клавдий Птолемей и многие другие, более поздние исследователи, к примеру, немецкий математик Карл Фридрих Гаусс и немецкий математик и геодезист Иоганн Генрих Луи Крюгер, в честь которых, собственно, и названа ортогональная проекция съемки местности, которая официальна для создания карт на территории России – поперечная цилиндрическая равноугольная картографическая проекция Гаусса-Крюгера).
При поиске данных о расстоянии по карте, особенно в полевых условиях, необходимо обратиться к самому начальному способу вычисления расстояния земного шара. Для этого вспомним два общеизвестных значения:
Длина экватора (40 000 километров);
Угол окружности земного шара (3600).
При простом арифметическом действии (40 000:360) получим количество километров в одном градусе на местности. При делении получим значение равное 111,1. Данное число означает, что в 10 географических координат карты мы имеем расстояние 111,1 километра. Данное число станет сложно вписать в процессе вычисления в масштаб карты и при поиске расстояния. Для более удобного расчета «древние» ввели более мелкое понятие, чем «градус». Более мелкой единицей градуса стала минута, а еще более мелкой – секунда. Данное решение было связано с периодом вращения земли вокруг своей оси, что аналогично составляло 3600 (в более подробные разъяснения данных вычислений можно прочитать в учебниках по геодезии и картографии).
Связав значения 111,1 (км) или 60 минут (60'), которые являются одинаковыми показателями для одинакового отрезка местности, а именно, 111,1 километра на местности равны 10 или 60' в сетке координат. Этим объясняется то, что угловое значение вращения земли можно приравнять к расстоянию. Данными изысканиями мы сможем пользоваться при расчете расстояний благодаря многолетним исследованиям астрономов, математиков, физиков и других именитых ученых. Мы же с вами производим для вычислений расстояний простые арифметические действия.
2 Способы измерения расстояния по картам разного масштаба
О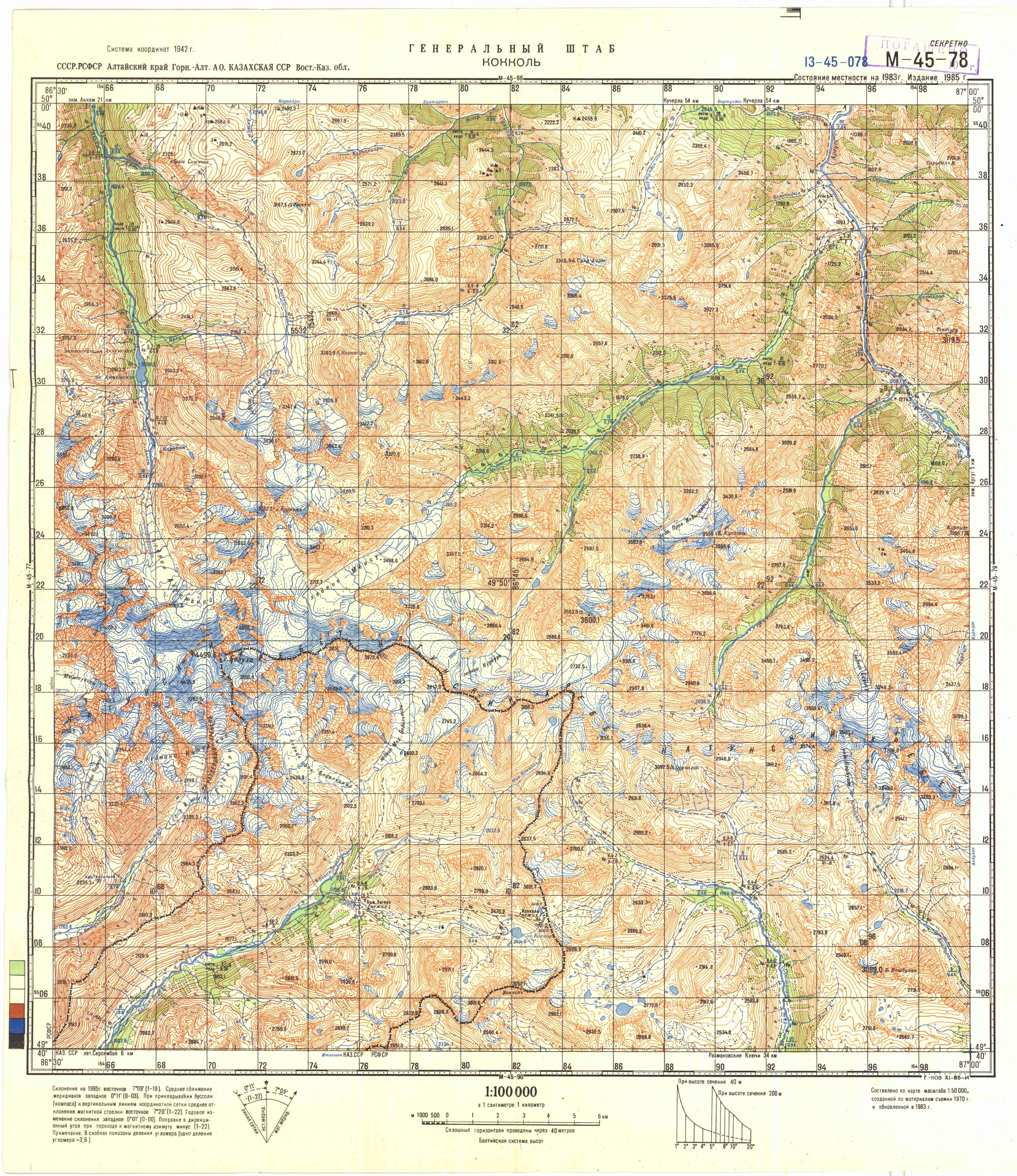 казавшись в ситуации, когда Вам в руки попала карта района будущего путешествия, нужно первым делом определить ее масштаб. Без знания масштаба никакими средствами не удастся рассчитать ни километраж будущего похода, ни чистое ходовое время по дням. Хорошо, если в распоряжении есть компьютер с выходов в интернет, где в нынешнее время можно скачать практически любую карту, особенно, если сервис, в котором происходит поиск карты, обладает автоматическим вычислением расстояния. Зачастую же бывает всё немного по-другому. При скачивании карты, к примеру, масштаба 1:100 000 (в 1 сантиметре на карте мы имеем 1 реальный километр расстояния), мы получаем карту хорошего качества с географическими координатами по краям карты (Приложение 1).
казавшись в ситуации, когда Вам в руки попала карта района будущего путешествия, нужно первым делом определить ее масштаб. Без знания масштаба никакими средствами не удастся рассчитать ни километраж будущего похода, ни чистое ходовое время по дням. Хорошо, если в распоряжении есть компьютер с выходов в интернет, где в нынешнее время можно скачать практически любую карту, особенно, если сервис, в котором происходит поиск карты, обладает автоматическим вычислением расстояния. Зачастую же бывает всё немного по-другому. При скачивании карты, к примеру, масштаба 1:100 000 (в 1 сантиметре на карте мы имеем 1 реальный километр расстояния), мы получаем карту хорошего качества с географическими координатами по краям карты (Приложение 1).
В данном случае перед нами карта, имеющая все три вида масштабов (именованный, числовой и линейный), а также рамки листа карты с имеющейся на ней градусной и минутной сеткой.
Таблица 1 «Виды масштабов на карте»
| Именованный масштаб – | В 1 сантиметре 1 километр |
| Числовой (численный) масштаб – | 1:100 000 |
| Линейный масштаб – | 
|
Вычисление расстояния, пройденного за день или весь период похода, можно произвести при помощи линейки, нитки, циркуля или курвиметра.
Допустим, при измерении отрезка по карте мы получили длину равную 20 сантиметров. Данное значение будет характеризовать лишь измеренную длину измеренного отрезка. Само же расстояние на этих 20 сантиметрах будет иным. Чтобы получить значение измеренного расстояния по карте нам необходимо полученное значение умножить на масштаб карты. В приведенном выше рисунке масштаб нашей карты 1:100 000. Это означает, что в 1 сантиметре на карте – 100 000 сантиметров на местности, то есть 1 километр (в данном случае измеренное расстояние мы будем умножать на 1).
При измерениях же по картам более крупного или более мелкого масштаба показания будут совсем иные (приведем в пример таблицу):
Таблица 2 «Перевод километража из численного в именованный»
| Измеренное расстояние (сантиметры) | Масштаб карты | Полученный километраж (километры) |
| Числовой | Именованный |
| 20 | 1:20 000 000 | В 1 см. 200 км. | 4 000 |
| 20 | 1:2 000 000 | В 1 см. 20 км. | 400 |
| 20 | 1:200 000 | В 1 см. 2 км. | 40 |
| 20 | 1:100 000 | В 1 см. 1 км. | 20 |
| 20 | 1:50 000 | В 1 см. 0,5 км. (500 м.) | 10 |
| 20 | 1:25 000 | В 1 см. 0,25 км. (250 м.) | 5 |
| 20 | 1:10 000 | В 1 см. 0,1 км. (100 м.) | 2,5 |
| 20 | 1:5 000 | В 1 см. 0,05 км. (50 м.) | 1 |
Данные измерения прекрасно производить в таблице Microsoft Excel, особенно при громоздких числовых объемах. Для обычного измерения нитки одного маршрута данных действий не требуется.
Для того, чтобы было проще ориентироваться в значениях, нужно запомнить всего одно правило: при переводе числового масштаба в именованный необходимо знать:
Таблица 3 «Перевод сантиметров на карте в километры на местности»
| Для получения километров | Отнимаем 5 последних цифр | 1:200 000 = 200 000 = в 1 см. 2 км. |
| Для получения метров | Отнимаем 2 последние цифры | 1:200 000 = 200 000 = в 1 см. 2 000 м. = 2 км. |
Данные «зачеркивания» прекрасно подходят при работе с большим количеством карт разного масштаба. Приведенный пример ниже станет наглядно демонстрировать, в каких случаях лучше отнимать два, а в каких – пять последних цифр (нулей):
Таблица 4 «Способы перевода расстояний по типам карт»
| Масштаб | Удобное отнятие | Результат (в 1 сантиметре) | Тип карты |
| 1:20 000 000 | 1:20 000 000 | 200 км. | Мелкомасштабные |
| 1:2 000 000 | 1:2 000 000 | 20 км. |
| 1:200 000 | 1:200 000 | 2 км. |
Среднемасштабные |
| 1:100 000 | 1:100 000 | 1 км. |
| 1:50 000 | 1:50 000 | 500 м. |
| 1:25 000 | 1:25 000 | 250 м. |
Крупномасштабные |
| 1:10 000 | 1:10 000 | 100 м. |
| 1:5 000 | 1:5 000 | 50 м. |
Таким образом, можно понять, что для мелкомасштабных и среднемасштабных карт прекрасно подходит вариант вычеркивания пяти нулей. Для карт крупномасштабных же подходит вариант вычеркивания двух последних нулей. При постоянной работе с картами данный навык закрепится очень быстро.
3 Вычисление расстояния по карте способом перевода временных характеристик в линейные
Теперь нам нужно найти расстояние по карте при отсутствии на ней масштаба. К примеру, если к нам в руки попала карта с обрезанным масштабом или увеличенная на принтере. Рассмотрим оба этих варианта.
1 вариант «Карта с обрезанным масштабом»
Данная карта (Приложение 2) имеет только рамки листа с нанесенными на нее географическими координатами.
О тсутствие на карте масштаба еще ни о чем не говорит, когда сохранены географические координаты. Вот по ним мы и начнем считать расстояние на карте для привязки и вычислению искомого масштаба. Данный способ прекрасно подходит и для второго варианта, когда карта увеличена на принтере, но на ней сохранена рамка карты с координатной сеткой.
тсутствие на карте масштаба еще ни о чем не говорит, когда сохранены географические координаты. Вот по ним мы и начнем считать расстояние на карте для привязки и вычислению искомого масштаба. Данный способ прекрасно подходит и для второго варианта, когда карта увеличена на принтере, но на ней сохранена рамка карты с координатной сеткой.
Первое, с чего необходимо начать вычисление – это широта. Из курса школьной географии нам известно, что широта – это те самые параллели, которые отходят от экватора к полюсам. Долготой же называется значение меридианов, которые как нарезанные арбузные корочки отходят от нулевого меридиана вправо (на восток) и влево (на запад) (для справки: нулевой меридиан отсчитывается от обсерватории в Великобританском городе Гринвич, что можно проследить по Карте Мира).
Итак, начинаем искать значение широт на данной карте. Они будут располагаться по левому или правому краям карты, так как значения от экватора к полюсам растут и, соответственно, будут указываться на левом и правом краях карты. Аналогично с долготами, значения которых в нашем полушарии растет слева направо, вследствие чего значения эти будут записаны на нижнем и верхнем краях карты. У нас данные числа будут следующими (Приложение 1 и 2):
Таблица 5 «Широты и долготы географических координат на карте»
| Широта (секунд'') | 34 | 36 | 38 | 40 |
|
| Долгота (секунд'') | 66 | 68 | 70 | 72 | 74 |
Д анные значения будут являться более мелкими делениями 1 градуса на карте, а именно, числа 34, 36, 38, 40; 66, 68, 70, 72, 74 будут являться минутами на карте. Для измерения расстояния в нашем случае координаты на углах карты для нас роли играть не будут (рисунок слева).
анные значения будут являться более мелкими делениями 1 градуса на карте, а именно, числа 34, 36, 38, 40; 66, 68, 70, 72, 74 будут являться минутами на карте. Для измерения расстояния в нашем случае координаты на углах карты для нас роли играть не будут (рисунок слева).
Зная данные значения на карте, можно с достаточной легкостью произвести вычисление расстояния. В данном случае необходимо найти отрезок, который будет составлять 1 километр на местности и не обязательно он будет равен 1 сантиметру на карте, даже если нам известно заранее, что карта была масштабом 1:100 000 (в причину того, что карта может быть увеличена на компьютере, масштаб карты соответственно изменится).
Первым делом нам необходимо найти километровое значение рамки квадрата листа карты, равное 2' (минуты).
Нам известно, что в 60' (или в 10) на карте находится 111,1 километра. Путем простого деления выясним километровое значение 2 минут:
60' = 111,1 км.;
2' = 111,1 / 30 = 3,7 (км.) – расстояние края квадрата карты (3,7 километров в 2 минутах на карте). Значение длин сторон квадратов будет одинаково. Для вычисления расстояния по карте этого будет вполне достаточно.
И так, для получения масштаба данной карты мы (в отличии от высококвалифицированных инженеров-геодезистов) можем принять другую меру длины на данном этапе вычисления. Для нас таковым станет мера квадрата карты равная 3,7 километрам. Но данное значение будет очень неудобным при расчетах. Поэтому проведем небольшие вычисления для получения «удобного» числа. Для этого совершим следующие действия, пока не получится приблизительно целое число:
так, для получения масштаба данной карты мы (в отличии от высококвалифицированных инженеров-геодезистов) можем принять другую меру длины на данном этапе вычисления. Для нас таковым станет мера квадрата карты равная 3,7 километрам. Но данное значение будет очень неудобным при расчетах. Поэтому проведем небольшие вычисления для получения «удобного» числа. Для этого совершим следующие действия, пока не получится приблизительно целое число:
3,7 (сторона квадрата) + 1,85 (половина стороны квадрата) = 5,55 (1,5 квадрата). Теперь 5,55 * 2 = 11,1 (3 стороны квадрата). На данном этапе можем удалить 11,1 – 0,1 = 11 (значение 0,1 (100 метров) компенсируется при умножении показателя вычисленного расстояния позднее, при добавлении коэффициента перепада высот, про который можно узнать в «Методических рекомендациях для обучающихся по специальности «Туризм» по измерению расстояния по карте»).
На данном этапе, вычленив целое число (11 километров), можно создать линейный масштаб следующим способом:
Разделить 11 километров на 11 частей при помощи линейки, в результате чего получим «удобное» значение для линейного масштаба и вычисления расстояния циркулем. Но деление возможно также на миллиметровой бумаге, что приведет к более точным расчетам.
Для данного способа будет более успешно проведение измерения только способом использования линейного масштаба, так как «привязаться» к масштабу в «1 сантиметре «Х» километров» не удастся в силу того, что карта увеличена и данный искомый «1 сантиметр» растянут.
Поэтому при данном измерении заблаговременно до планируемого путешествия необходимо произвести все картографические изыскания в домашних или учебных условиях, чтобы не заблудиться на пересеченной местности в походе, когда под рукой не окажется ни карандаша с циркулем, ни миллиметровой бумаги.
Но более верным способом откалибровать карту по масштабу окажется сравнение исходной карты (с нанесенным на нее масштабом) с картой увеличенной и распечатанной. В данном случае можно будет методом пропорции найти искомый масштаб.
Н апример, если на данном участке карты масштаб был таковым:
апример, если на данном участке карты масштаб был таковым:
 ,
,
То на карте, увеличенной масштаб мы сможем увеличить способом умножения во столько же раз, во сколько изменилось значение одной стороны квадрата (см. ниже).
О собенно действенным способом увеличения масштаба карты является способ одновременного увеличения карты совместно с масштабом этой карты, а не ее отдельных фрагментов. Но если же необходим отдельный фрагмент, то можно в программе «Paint» перенести масштаб в нужное место, после чего нужный фрагмент карты увеличить и распечатать.
собенно действенным способом увеличения масштаба карты является способ одновременного увеличения карты совместно с масштабом этой карты, а не ее отдельных фрагментов. Но если же необходим отдельный фрагмент, то можно в программе «Paint» перенести масштаб в нужное место, после чего нужный фрагмент карты увеличить и распечатать.

Приложения
Приложение 1 «Карта района путешествия»

Приложение 2 «Карта с обрезанным масштабом»

14








 казавшись в ситуации, когда Вам в руки попала карта района будущего путешествия, нужно первым делом определить ее масштаб. Без знания масштаба никакими средствами не удастся рассчитать ни километраж будущего похода, ни чистое ходовое время по дням. Хорошо, если в распоряжении есть компьютер с выходов в интернет, где в нынешнее время можно скачать практически любую карту, особенно, если сервис, в котором происходит поиск карты, обладает автоматическим вычислением расстояния. Зачастую же бывает всё немного по-другому. При скачивании карты, к примеру, масштаба 1:100 000 (в 1 сантиметре на карте мы имеем 1 реальный километр расстояния), мы получаем карту хорошего качества с географическими координатами по краям карты (Приложение 1).
казавшись в ситуации, когда Вам в руки попала карта района будущего путешествия, нужно первым делом определить ее масштаб. Без знания масштаба никакими средствами не удастся рассчитать ни километраж будущего похода, ни чистое ходовое время по дням. Хорошо, если в распоряжении есть компьютер с выходов в интернет, где в нынешнее время можно скачать практически любую карту, особенно, если сервис, в котором происходит поиск карты, обладает автоматическим вычислением расстояния. Зачастую же бывает всё немного по-другому. При скачивании карты, к примеру, масштаба 1:100 000 (в 1 сантиметре на карте мы имеем 1 реальный километр расстояния), мы получаем карту хорошего качества с географическими координатами по краям карты (Приложение 1). анные значения будут являться более мелкими делениями 1 градуса на карте, а именно, числа 34, 36, 38, 40; 66, 68, 70, 72, 74 будут являться минутами на карте. Для измерения расстояния в нашем случае координаты на углах карты для нас роли играть не будут (рисунок слева).
анные значения будут являться более мелкими делениями 1 градуса на карте, а именно, числа 34, 36, 38, 40; 66, 68, 70, 72, 74 будут являться минутами на карте. Для измерения расстояния в нашем случае координаты на углах карты для нас роли играть не будут (рисунок слева). так, для получения масштаба данной карты мы (в отличии от высококвалифицированных инженеров-геодезистов) можем принять другую меру длины на данном этапе вычисления. Для нас таковым станет мера квадрата карты равная 3,7 километрам. Но данное значение будет очень неудобным при расчетах. Поэтому проведем небольшие вычисления для получения «удобного» числа. Для этого совершим следующие действия, пока не получится приблизительно целое число:
так, для получения масштаба данной карты мы (в отличии от высококвалифицированных инженеров-геодезистов) можем принять другую меру длины на данном этапе вычисления. Для нас таковым станет мера квадрата карты равная 3,7 километрам. Но данное значение будет очень неудобным при расчетах. Поэтому проведем небольшие вычисления для получения «удобного» числа. Для этого совершим следующие действия, пока не получится приблизительно целое число:  апример, если на данном участке карты масштаб был таковым:
апример, если на данном участке карты масштаб был таковым: ,
,









