Методика изучения теорем в курсе геометрии 7-9 классов
МКОУ «Черницынская СОШ» Октябрьского района Курской области
Учитель математики Ященко Е.А.
Пропедевтика (до изучения теорем)
Формировать у учащихся умения подмечать закономерности.
Воспитывать у школьников понимание необходимости доказательства.
Обучать учащихся умению выделять условие и заключение в математических утверждениях.
Знакомить учащихся с простыми и сложными высказываниями и значениями их истинности.
Знакомить школьников с понятием отрицания высказываний и с понятием противоречивых высказываний.
Обучать учащихся умению выделять различные конфигурации на одном и том же чертеже.
Обучать школьников умению пользоваться контрпримерами.
Обучать учащихся умению выполнять геометрические чертежи и читать их.
Формировать у учащихся умения выводить следствия из заданных условий.
Формировать у учащихся умения проводить доказательные рассуждения, делать выводы.
При изучении теоремы
ПОДГОТОВКА
Включить в материал для повторения (актуализация может быть проведена непосредственно перед доказательством теоремы или на предыдущем уроке) понятия, теоремы, аксиомы, на которых строится доказательство изучаемой на уроке теоремы. Решить задачи, которые помогут осуществить доказательство. Подвести детей к изучению (возможно, формулировке) теоремы с помощью проблемной ситуации.
РАБОТА НАД ФОРМУЛИРОВКОЙ
Провести анализ формулировки теоремы с целью выделения разъяснительной части, условия и заключения теоремы, предусмотреть ошибки, которые могут допустить учащиеся в формулировке теоремы и подготовить соответствующий контрпример. Предложить задание на переформулировку теоремы из категоричной формы в условную и наоборот. Разобрать с учащимися, о свойстве или о признаке идет речь в теореме.
РАБОТА НАД ДОКАЗАТЕЛЬСТВОМ
Определить ведущий метод доказательства, исследовать особенности доказательства. Выработать с учащимися план доказательства теоремы. Найти другие способы доказательства.
ОФОРМЛЕНИЕ
Оформить теорему в письменном виде
ЗАКРЕПЛЕНИЕ
Решить задачи, закрепляющие теорему.
Разберем все этапы работы над теоремой на примере изучения теоремы Пифагора
ПОДГОТОВКА
Перед доказательством теоремы Пифагора желательно провести подготовительную работу по готовым чертежам и повторить основные понятия, определения, термины: прямоугольный треугольник, катет, гипотенуза, прямой угол, прямоугольник, квадрат и т.д.; формулы и свойства площадей, так как в доказательстве используется площадь квадрата и площадь прямоугольного треугольника, признаки равенства прямоугольных треугольников и т.д.
РАБОТА НАД ФОРМУЛИРОВКОЙ
Для того, чтобы дать ответ на вопрос: «О свойстве или о признаке идет речь в теореме?», нужно предложить учащимся теорему сформулировать в условной форме (если окажется, что рассматриваемое понятие находится в условии теоремы, то теорема выражает свойство этого понятия, если же понятие находится в заключении теоремы, то она выражает признак).
Теорема Пифагора в категоричной форме: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Переформулировав теорему из категоричной формы в условную, дети будут иметь: «Если треугольник прямоугольный, то квадрат гипотенузы равен сумме квадратов катетов». Тогда можно будет сделать вывод: поскольку понятие «прямоугольный треугольник» находится в условии теоремы, то она выражает собой свойство этого понятия.
РАБОТА НАД ДОКАЗАТЕЛЬСТВОМ
Определить ведущий метод доказательства - доказательство способом достроения квадрата, исследовать особенности доказательства, выработать с учащимися план доказательства теоремы. Найти другие способы доказательства:
доказательство, используя пропорциональные отрезки;
доказательство, используя подобие треугольников и т.д.
Можно продемонстрировать учащимся некоторые методы доказательства на презентации.
План доказательства:
Выполнить дополнительные построения
Доказать равенство прямоугольных треугольников
Доказать, что АМКВ – квадрат
Найти площадь квадрата CDFE различными способами, приравнять площади и упростить полученное выражение.
ОФОРМЛЕНИЕ
Оформить теорему в письменном виде
|
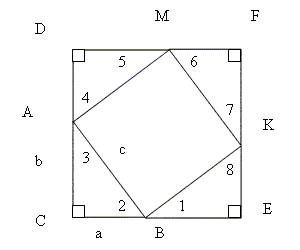
Дано: ΔАВС – прямоугольный ВС=a АС=b АВ=с Доказать: с2 = а2 + в2
| 
|
| Доказательство: Достроим этот треугольник до квадрата со стороной a+b следующим образом: Продолжим стороны АС и ВС за точки А и В соответственно, от точки А на продолжении стороны АС отложим отрезок, равный а, а от точки В на продолжении стороны ВС отрезок, равный b. Обозначим полученные точки D и E соответственно. Через Е проведём прямую, параллельную АС, а через точку D прямую, параллельную СВ. Обозначим точку пересечения проведённых прямых за F. От точки F на отрезке DF отложим отрезок, равный а, а на отрезке FE, отрезок, равный b. Обозначим получившиеся точки М и К соответственно. Проведём отрезки АМ, МК и ВК. Полученный квадрат состоит из 4 равных прямоугольных треугольников (по 2 катетам) и одного четырёхугольника – квадрата (все стороны и все углы равны: каждый угол четырёхугольника равен 1800 минус сумма углов, например 2 и 3, т.е. все углы четырехугольника равны 900) Площадь большого квадрата равна (a+b)2, а с другой стороны с2 +2(ab). Т.е. получили равенство: (a+b)2= с2 +2(ab). После раскрытия скобок и упрощения получим с2 = а2 + в2 ,что и требовалось доказать
|
ЗАКРЕПЛЕНИЕ
После оформления доказательства стоит задать учащимся вопросы, связанных с зависимостью сторон прямоугольного треугольника:
Очевидно, нет, так как две стороны треугольника a и b не определяют однозначно его форму, а третья сторона меняет свою длину в зависимости от значения угла между сторонами a и b так, что a – b
Верна ли обратная теорема, обратная теореме Пифагора?
Если квадрат большей стороны равен сумме квадратов двух других сторон, то треугольник прямоугольный, а именно: прямым является угол, лежащий против этой большой стороны. В самом деле, если бы это было не так и треугольник, стороны которого a, b и c связаны зависимостью c2 = a2 + b2, оказался бы не прямоугольным, то и стороны бы его не смогли бы удовлетворять этому равенству.
Весьма полезно попросить учащихся указать ряд случаев применения теоремы Пифагора. Затем можно решить устные задачи, закрепляющие теорему:
Катеты прямоугольного треугольника 6 см и 8 см. Вычислите гипотенузу треугольника.
Гипотенуза прямоугольного треугольника равна 5 см, а один из катетов 3 см. Определите второй катет.
Также после изучения теоремы Пифагора можно предложить учащимся такую задачу: «Гипотенуза и один из катетов прямоугольного треугольника пропорциональны гипотенузе и катету другого прямоугольного треугольника соответственно, причем коэффициент пропорциональности равен К. Найдите отношение других катетов. Сформулируйте ответ в виде теоремы». Задать вопрос: при изучении какой темы целесообразно использовать данную задачу?
Вопросами для повторения предусматриваются доказательства следствий из теоремы Пифагора. Эти доказательства просты и в явном виде в учебном пособии отсутствуют. При разборе этих доказательств в классе можно предложить учащимся записать их в тетради.

















