Методика обучения решению текстовой задачи различными способами.

ГБОУ ДПО «СЕВЕРО - ОСЕТИНСКИЙ РЕСПУБЛИКАНСКИЙ ИНСТИТУТ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ РАБОТНИКОВ ОБРАЗОВАНИЯ».

МБОУ ГИМНАЗИЯ № 4 Г.ВЛАДИКАВКАЗ

МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ТЕКСТОВОЙ ЗАДАЧИ РАЗЛИЧНЫМИ СПОСОБАМИ.

Чукаева Валентина Алексеевна

учитель математики

МБОУ гимназии № 4

г. Владикавказ

2020 год

Содержание.

1. Аннотация……………………………………………… .3

2. Слово о педагоге………………………………………. . 4

3. Описание опыта………………………………………… 7

4. Литература……………………………………………… 30

5. Приложение 1…………………………………………… 31

6. Приложение 2…………………………………………… 34

7. Приложение 3…………………………………………… 36

8. Приложение 4 …………………………………… …….. 46

АННОТАЦИЯ.

В данной работе содержится методический материал, предназначенный для развития умственных и творческих способностей как учащихся, так и учителей. Иногда привитый нам с детства навык мыслить последовательно с помощью алгоритма оказывается бесполезен при решении многих типов задач. Какие-то строгие правила, алгоритмы создают рамки и лишают человека возможности свободно развивать собственные творческие индивидуальные способности. Умение мыслить гибко, рассматривать проблему с разных сторон, не бояться приступить к решению нестандартной задачи, которую раньше не встречал, осмысленно и вдумчиво читать - самые необходимые на сегодня навыки, без которых невозможно достичь личного профессионального творческого успеха.

Автор работы на своем личном педагогическом опыте показывает, как расширять и развивать индивидуальные умственные и творческие способности учащихся на примере осмысленного чтения задачи, анализа ее условия, поиска различных способов решения, оценки влияния величин на поставленный вопрос.

Работа адресована широкому кругу читателей, так как универсальна, проста в изложении и доступна для понимания любым читателем. Учитель по любому предмету может использовать данную работу как методическое пособие, для ознакомления с основными приемами при планировании урока по ФГОСам. В основе ФГОС лежит системно деятельностный подход, одной из ключевых категорий которого является «деятельность». Урок всегда должен рассматриваться не только как деятельность учителя, но и как деятельность ученика, и строиться с учетом партнерства учителя и ученика, их взаимодействия, личностной ориентации и индивидуализации образовательного процесса. Таким образом, целью данной работы является оказание помощи педагогам в стимулировании поиска своих индивидуальных подходов при проектировании современного урока.

СЛОВО О ПЕДАГОГЕ.

Автором данной работы является учитель математики МБОУ гимназии № 4 г. Владикавказа Чукаева Валентина Алексеевна.

Учитель имеет два высших образования. В 1985 году Валентина Алексеевна окончила СКГМИ по специальности инженер-строитель, а в 1995 году получила диплом Северо-Осетинского государственного университета им. К. Хетагурова по специальности «Математика» с присвоением квалификации «Математик. Преподаватель».

Общий стаж работы Чукаевой В.А. составляет 36 лет, из них педагогический стаж-29 лет.

В 2002 году учителю была присвоена первая квалификационная категория. С 1.09.2007 года Чукаева В.А. имеет высшую квалификационную категорию.

С 1992 г. по 1996 г. Валентина Алексеевна работала учителем математики в МБОУ СОШ № 46, а с 1996 г. по 2011г. в МБОУ СОШ № 39. В 2008 г. была назначена Зам.директором по УВР МБОУ СОШ № 39. С 1.09.2011 года и по сей день Чукаева В.А. работает в МБОУ гимназии № 4 учителем математики и является руководителем Методического Совета школы.

Учитель активно участвовал в городских конкурсах профессионального мастерства «Учитель года» в 1999 и 2008 годах. Имеет дипломы и грамоты, подтверждающие высокий профессионализм и творческий подход к выполнению конкурсных заданий.

Чукаева В.А. регулярно занимается своим самообразованием. С 2015 года была участником VI, VII, VIII и IX Республиканских сессий ЛМШУ.

Ежегодно учитель проходит различные курсы повышения квалификации, принимает активное участие в подготовке экспертов региональной предметной комиссии по математике для проведения итоговой аттестации по образовательным программам среднего общего образования (2017,2019, 2021 годов), имеет сертификат участника семинара «Особенности реализации учебных программ и учебно-методического комплекта по математике в школе в условиях ФГОС», имеет благодарственные письма от Северо-Осетинского республиканского института повышения квалификации работников образования за вклад в развитие системы повышения квалификации учителей математики и распространение собственного педагогического опыта. В рамках курсов повышения квалификации учитель представила опыт работы по темам «Методика подготовки учащихся по математике к ОГЭ 2018 с использованием результатов ОГЭ 2017 года», «Решение задач повышенной сложности», «Решение 19 задания «Числа и их свойства» по профильной математике», «Решение текстовых задач (11 задание по профильной математике) с помощью отрезков». «Опыт методической работы по учебникам математики для 5 и 6 классов под редакцией С.М. Никольского». Выступает с докладами на заседаниях городского методического объединения математиков.

Чукаева Валентина Алексеевна имеет две печатные работы: «Обучение смысловому чтению-основная цель преподавания математики», «Практически - направленное изучение форм окружающего мира – основная задача геометрии», которые опубликованы в сборнике учебно-методических материалов работников образования РСО-Алания «Педагогический опыт: проблемы и находки».

Современный урок должен соответствовать требованиям ФГОС. Для Чукаевой В.А. именно методика преподавания математики становится главенствующей на уроке. Учитель может знать математику, но научить ребенка своему предмету удается не каждому. Между «знать» и «научить» стоит огромная пропасть. Сейчас в российских школах на первое место ставится наличие методически грамотных кадров. Это процесс не одного дня. Когда учитель приходит работать в школу, то он может знать математику, но научить этому учащихся, передать им знания оказывается сложным долгим и кропотливым процессом. Простое зазубривание формул, правил, теорем без понимания не приносит ощутимых результатов. Поэтому преподаватель оказывает методическую помощь учителям не только в своей школе, но и в республике.

За время работы в школе Чукаева В.А. наработала методику преподавания математике, где, по ее мнению, на первом месте должна стоять работа с книгой и осмысленное чтение теории. Перед учащимися учитель ставит проблему, решение которой они должны найти самостоятельно. Можно забыть то, что запомнил, но невозможно забыть то, что понял и глубоко осмыслил. Понимание теории проверяется при практическом решении задач. Самостоятельной работе учащихся учитель всегда отводит главное место. Она сторонник минимализма теории и простоты при решении задач.

Учитель считает, что повышенная трудность, громоздкость, невнятная постановка вопроса во многих заданиях не повышает уровень владения предметом, а убивает желание найти правильное решение. Бесконечные трудоемкие самостоятельные работы на 10-15 минут в конце каждого урока без последующей работы над ошибками убивают интерес к изучаемому предмету, заставляют многих делать вывод о том, что математика – непосильна для изучения и усвоения. На каждом уроке автор этого опыта добивается простоты и глубины изложения материала. «Век живи – век учись» - это девиз работы учителя.

В данной работе учитель излагает методику преподавания предмета по учебнику «Математика 5 класс» и «Математика 6 класс» под редакцией С.М. Никольского с последующем использованием данных навыков при решении текстовых задач на ОГЭ и ЕГЭ,

Учитель имеет опыт работы с детьми с особенностями развития. Она получила удостоверение по прохождению курсов по теме: «Эффективные практики реализации адаптированных основных образовательных программ для детей с ОВЗ: межпредметные технологии». Особенно ее интересует проблема обучения детей-дислексиков математике. Для Чукаевой В.А. не существует детей, которым, по мнению других, закрыт путь в математику. Она считает, что в любом возрасте можно начать учиться серьезно. Главное - иметь мотивацию, трудолюбие и наставника. Многие ее учащиеся сейчас занимаются фундаментальной наукой в различных областях. Математикой увлекся ее бывший ученик Гуев Т.А., который сейчас преподает в Москве.

Учитель активно участвует в реализации образовательной программы с применением инновационных цифровых ресурсов (Якласс, РЭШ), о чем свидетельствуют полученные ею сертификаты, ведет свой сайт на Мультиуроке, где делится своими методическими разработками с учителями России.

ОПИСАНИЕ ОПЫТА.

«Хороших методов существует ровно столько, сколько существует хороших учителей»

(Д. Пойа)

Тема опыта: Решение текстовых задач по математике различными способами в 5-6 классах.

Основной задачей современного учителя математики является не создание у учащихся простого запоминания знаний, а затем их механического применения, а культивирование умения мыслить самостоятельно, устанавливать связи между величинами, а потом применять его в нестандартных ситуациях. Конечно, никто не принижает роли вычислительных навыков. Человек, который может скрупулезно проводить сложные вычисления, но не умеет анализировать данные задачи, составлять уравнения, прогнозировать влияние изменения какой-нибудь величины на конечный результат, не может с пользой применить высокую вычислительную культуру при решении различного рода задач. Понимание смысла задачи и осознанный поиск ее решения – основная цель обучения учащегося. Такой подход к изучению материала нужен на любом уроке по любому предмету

Каждый учитель мечтает поднять процент качества образования в своих классах. Мы сами с вами можем знать многое, многое понимать, решать различные задачи. Но как доступно и просто передать свои знания другим? На практике это оказывается делом непростым. И здесь на первое место выходит методика преподавания предмета. Я хочу поделиться некоторыми своими приемами при изложении конкретных тем по математике.

Единицам из моего класса достаточно для понимания темы простого объяснения учителем новой темы на уроке. Затем при выполнении домашнего задания они еще раз закрепят пройденный материал и обнаружат непонятые моменты, а на следующем уроке при проверке домашнего задания получат ответы на возникшие у них вопросы. А как быть тем, кто при объяснении нового материала просто запомнил теорию, а потом при решении задачи понял, что даже не имеет представления о смысле решения заданного задания. Как же научиться применять свои знания на практике? Это является трудным кропотливым ежедневным трудом. В этом случае именно проблемное обучение становится главным средством достижения этой цели. То, что добыто своим трудом на уроке, становится понятно, бесценно для ученика. Оно останется навсегда знанием, которое в будущем станет твердым фундаментом для дальнейшего роста ученика.

Из-за специфики моей работы мне приходится ежедневно посещать уроки учителей не только математики, но и других школьных дисциплин. Часто создается впечатление, что преподаватели сами не до конца понимают смысла того, что они излагают на уроке. Урок напоминает лекцию, которую проводит учитель, демонстрируя свои знания по предмету. При этом педагог не имеет обратной связи с аудиторией, не использует теорию учебника для изложения нового материала, не продумывает тщательно все этапы урока, не понимает концепции обучения по рекомендуемому учебнику. Использование на уроке презентации и строгое соблюдение этапов урока не гарантирует осознанного усвоения учеником излагаемой учителем новой темы. Передать ученику знание-самый трудный, долгий, одновременно простой и радостный процесс.

Особенно хочется помочь учителям математики. Учитель учится каждый день. Ему должны быть интересны новые открытия в его дисциплине, новые книги, новые методы обучения. Но на деле часто наблюдается профессиональное застывание и выгорание, неумение приспособиться к новым условиям, нежелание работать над собой, идет отторжение новых учебников, программ. Я ни коем случае не говорю о том, что все, что нам предлагают новое, – это правильное, целесообразное и грамотное. Мы вправе сами выбирать, что нам подходит, что доступно для нашего понимания, но отрицать целесообразность своего роста в педагогике является преступлением.

Цель данной работы – помочь учителю разобраться в методике преподавания предмета. Именно методика выходит на первое место при изложении любой темы на уроке для повышения качества образования.

Если учитель может сам вырабатывать методику изложения какой-либо темы, то это является гарантией того, что он сможет передать ученику свои знания на должном уровне и с минимальными потерями. Методика учителя шлифуется годами. Она бесценна.

В каждом ребенке заложена природная любознательность, которую нам учителям следует использовать во благо. В словаре В. Даля дается следующее определение: «Любознание, любознательность – дельное любопытство, любовь к наукам, к познаниям, желание поучаться».

«Любопытство. С него все и началось»,-написали П. Джеймс и Дж. Мартин.

Как не согласиться с этой истиной! Именно проблемное обучение математике, опирающееся на детское «дельное любопытство», может дать весомый результат в умственном и творческом развитии ребенка.

Я работала и работаю по сей день в обыкновенной школе с обыкновенными учениками, которые не обладают какими-либо сверхспособностями. В нашей школе учатся дети из разных социальных групп. Часто ты оказываешься единственным человеком в жизни ребенка, который контролирует его учебу. В этом случае мне легче увидеть результаты своей работы - это развитое тобой его «дельное любопытство». Именно работа с такими детьми позволяет учителю шлифовать свое педагогическое мастерство. Работа с одаренными и мотивированными детьми - счастье для любого педагога. А что делать, если эти качества отсутствуют у твоих учеников? Таких детей тоже надо учить на совесть. В этом случае на первое место выходит педагогическое мастерство самого учителя. Здесь без четкой и продуманной методики не обойтись.

Начало серьезной работе над задачей было положено в 2015 году после занятия по теме «Реализация деятельного подхода (ДП) и личностно- ориентированного обучения (ЛОО) при работе с текстовой задачей. Обучение проводила Малова И.Е. (доктор педагогических наук, профессор Брянского государственного университета имени академика И.Г. Петровского). Лектор в очень подробной форме изложила нам теорию по данному вопросу. Потом нам было предложено решить текстовые задачи различными способами. Особенно лектор акцентировала наше внимание на том, чтобы мы попробовали решить задачу тем способом, который мы редко используем.

Я попробовала решить задачу (Приложение 4) комбинированным способом, используя отрезки и арифметический способ. До этого момента я думала, что такая задача решается только с помощью уравнения. Малова И.Е. на этом вебинаре предложила мне объяснить своим коллегам суть моего решения и ответить на интересующие их вопросы.

Потом Малова И.Е. предложила нам провести исследовательскую работу по теме «Некоторые приемы поиска способа решения задач». Лектор подробно дала нам рекомендации в виде презентации. Перед нами была поставлена проблема: что делать учителю, чтобы научить учащихся решать задачи. Тип задач выбирался нами самостоятельно. Это могли быть текстовые алгебраические или геометрические задачи. Перед нами ставилась цель: выявить и показать на примерах некоторые приемы поиска способа решения задач. Для достижения этой цели мы должны подумать и решить следующие задачи:

1.Изучить литературу по проблеме….

2.Выявить ситуации необходимости….

3.Разработать методические рекомендации

по выявленным ситуациям…

Данная работа открыла мне новый уровень понимания математики. Я поняла, что современная система образования должна быть нацелена на то, чтобы помочь детям проявить себя, создать условия для удовлетворения их индивидуальных интеллектуальных способностей, формирования научных взглядов на мир. Работа над задачей является творческой деятельностью. Очень важно на этом этапе привить обучаемым навыки самостоятельной творческой деятельности. Только при самостоятельной работе воспринятая информация перерабатывается в знания, а знания в умения и навыки. Формирование умений самостоятельной работы должны закладываться у обучаемых в школе, конечно, при изучении различных дисциплин.

Позже мне стали все чаще на практике встречаться учащиеся, которые решали текстовые задачи нетрадиционными способами. Используя свой способ решения, они получали правильный ответ, но их рассуждения отличались от традиционных.

Все это натолкнуло меня на более серьезную работу над задачей. Я стала рассматривать этот тип работы на уроке с особой скрупулезностью. Стала работать над этой темой, начала изучать методическую литературу, собирать материал, продумывать очень тщательно ход урока при решении задачи.

Я хочу показать итог своей работы над этим вопросом в данном опыте. Здесь изложена конкретная методика обучения решению текстовых задач разными способами по учебникам С.М. Никольского «Математика 5 класс» и «Математика 6 класс». В приложениях рассмотрено решение конкретных задач разными способами. Мы привыкли годами автоматически работать по одной и то же книге, иной раз даже не особо задумываясь о смысле разбираемого нами на уроке материала. Именно это не позволяет нам расширять горизонты нашего познания, не дает шанс поднять наше профессиональное мастерство на следующий новый более высокий уровень. Многие учителя до сих пор не хотят менять учебник. Они настаивают на нецелесообразности смены порядка изучения тем. Поэтому многие мои коллеги до сих пор не приняли простой и лаконичный метод интервалов, не используют единичную окружность при решении тригонометрических уравнений и неравенств, в частности при отборе принадлежности корней заданному промежутку.

Когда я впервые столкнулась с учебниками математики под редакцией С.М.Никольского, мне показалось, что учебник слишком труден для обучения по нему учащихся 5-х и 6-х классов. Особенно поразил меня новый подход к решению текстовых задач в 5 и 6 классах. Но потом, проработав по учебнику два года, я поняла строение учебника. Все практические задания, которые излагаются после теории, надо выполнять в строго определенном порядке. Они подобраны таким образом, чтобы, начиная с первых более легких заданий, ученик, постепенно набираясь опыта при решении заданий и углубляясь при этом в суть теории, в конечном итоге пытался сам приступить к решению более сложных задач, не замечая уровня сложности задания. Когда я детально стала изучать тему за темой, пытаясь понять смысл каждого задания, я обнаружила, что многие темы излагаются в этом учебнике именно таким образом, какой мне открылся после 25 лет педагогической работы учителем. Многие мои собственные выводы и наблюдения по изложению каких-то тем в этом учебнике оказались прописанными в теоретическом материале.

Работа по этому учебнику вывела меня на более серьезный глубокий, главное новый, уровень понимания математики, особенно при решении текстовых задач.

Задачи в учебнике изложены таким образом, чтобы ребенок не подсел на применение алгоритма решения какого-либо конкретного типа задач, а смог развивать свое мышление, не привязываясь к схеме, а используя свои собственные индивидуальные способности. Некоторые задачи, которые я раньше решала с учениками 8-9 классов или при подготовке к ОГЭ и ЕГЭ с помощью рациональных уравнений, теперь оказались в учебниках для 5 и 6 классов, и как оказалось, их теперь можно решить с помощью отрезков. Опыт показывает, что решение задач разными способами побуждает учащихся к поиску различных способов решения. Это в конечном счете приводит к развитию их индивидуальных творческих способностей

Часто из начальной школы в 5 класс приходят ученики с чувством наличия у них ложного умения решать задачи. Ученики и их родители часто доказывают мне, что можно решить задачу без краткой записи условия, без пояснений. Отсюда, как следствие, вытекает конфликт преемственности начальной и старшей школ. Умение решать задачи по типам с помощью алгоритма, без понимания условия задачи часто принимается за серьезное понимание математики. Учащийся чаще всего не в состоянии сделать краткую запись к задаче. не может ответить на элементарные вопросы по условию или объяснить выбор использования им того или иного арифметического действия.

В учебнике задачи излагаются в определенном порядке от простой к сложной. Здесь продуман каждый шаг. Каждая предыдущая задача является кирпичиком для решения следующей более сложной.

Имеющаяся дополнительная дидактическая литература к учебнику не позволяет углублять знания по предмету. Авторы этих разработок не ознакомились детально с учебником, не поняли основные концепции изложения материала, а просто добавили задания по темам, не учитывая специфику изложения материала в данном пособии и возрастных особенностей учащихся. Только дидактические материалы с рекомендуемыми самостоятельными и контрольными работы гармонично дополняют учебник, предлагая разнообразные задания, которые не дублируют учебник, а предлагают широкий спектр выбора заданий от простого к сложному.

В процессе обучения математике задачи выполняют разнообразные функции. Учебные математические задачи являются очень эффективным и часто незаменимым средством усвоения учащимися понятий и методов школьного курса математики, вообще математической теории. Велика роль задач в развитии мышления и в математическом воспитании учащихся, в формировании у них умений и навыков практического применения математики. Решение текстовых задач является главной ступенью к достижению всех тех целей, которые ставятся перед математикой.

В тематическом планировании для решения задач отводится недостаточное количество учебного времени, поэтому только правильная методика обучения решению математических задач сможет оказать существенную роль в формировании высокого уровня математических знаний, умений и навыков учащихся.

Актуальность опыта заключается в том, что решение текстовых задач различными способами сможет повысить качество знаний не только по математике, но и способствует повышению качества знаний по всем другим предметам. Текстовые задачи, на мой взгляд, трудный и интересный материал. Однако в школьном курсе математики не всегда удается уделить этой важной теме достойное внимание, хотя именно решение задачи способствуют развитию логического мышления, математической речи, повышению математической культуры. Данная тема интересна тем, что она позволяет находить новые неординарные подходы к решению задач, ведь многие текстовые задачи очень тяжело и громоздко решаются аналитическим путем. Научившись решать задачи различными способами, ученик сможет применить этот навык не только на уроках математики, но и при решении задач по другим предметам, а потом в дальнейшей жизни, то есть раскрыть свои индивидуальные способности.

Целью данной работы является выявление теоретических и методических основ привития познавательного интереса к математике, развития творческих индивидуальных качеств ученика в процессе учебной деятельности при решении текстовых задач различными способами, способствующих формированию познавательного интереса при обучении математике в 5 - 6 классах.

Объект исследования: текстовые задачи в курсе математики 5-6 классов по учебникам С.М.Никольского.

Предмет исследования: способы решения текстовых задач.

Проблема: а) в школьном курсе изучения математики используется ограниченное количество способов решения текстовых задач, б) очень малое время отведено в программе решению задач.

Гипотеза: а) с помощью различных способов можно упростить и ускорить процесс решения текстовых задач, б) тщательная работа над условием задачи, поиск способа решения задачи, формирование умения устанавливать связи между величинами развивает и формирует умение думать, которое является главной целью обучения.

ТЕХНОЛОГИЯ ОПЫТА

При обучении математике задачи имеют большое и многостороннее значение.

Известный математик и педагог Алексей Иванович Маркушевич говорил: «Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели».

Образовательное значение математических задач. Решая математическую задачу, человек познаёт много нового: знакомится с новой ситуацией, описанной в задаче, учится применять математическую теорию к её решению, исследует и продумывает новые методы решения, находит связи между величинами, закрепляет теоретические разделы математики, необходимые для решения задачи, и т.д. Иными словами, при решении математических задач человек приобретает математические знания, повышает своё математическое образование, углубляет практические навыки использования своих знаний для построения модели решения любой задачи по любому предмету. При решении некоторого типа задач у ученика формируется умение решать задачи, а при достаточной тренировке – и навык, который позволяет находить решение любой нестандартной задачи.

Практическое применение математических задач. При решении математических задач ученик обучается применять математические знания к практическим нуждам, готовится к практической деятельности в будущем, к решению задач, выдвигаемых практикой, повседневной жизнью. Почти во всех конструкторских расчётах приходится решать математические задачи, исходя из запросов практики. Исследование и описание процессов и их свойств невозможно без привлечения математического аппарата, т.е. без решения математических задач. Математические задачи решаются в физике, химии, биологии, сопротивлении материалов, электро- и радиотехнике, особенно в их теоретических основах, и др.

Это означает, что при обучении математике учащимся следует предлагать задачи, связанные со смежными дисциплинами (физикой, химией, географией и др.), а также задачи с техническим и практическим, жизненным содержанием.

Значение математических задач в развитии мышления.

Очень велико развивающее значение математических задач.  Решение математических задач приучает выделять условие и заключение, анализировать данные, находить общее, и особенно в данных, сопоставлять и противопоставлять факты, проверять правильность нахождения искомой величины исходя из условия данной конкретной задачи, прогнозировать результат, который может получиться в задаче, отрабатывать навыки нестандартного выполнения арифметических действий, используя законы сложения, умножения. При решении математических задач воспитывается правильное мышление, но прежде всего, учащиеся приучаются к полноценной аргументации.

Огромная значимость нахождения школьниками различных способов решения одной задачи по математике не раз отмечалась на страницах методической литературы. Однако наблюдения показывают, что на уроках, как правило, рассматривается лишь один способ решения задачи, причём не всегда наиболее рациональный. Проводимая в таких случаях аргументация в виду отсутствия достаточного количества времени, отводимого на решение одной задачи, не имеет под собой основы: для математического развития учащихся, для развития их творческого индивидуального мышления гораздо полезнее решить одну задачу разными способами (если это возможно) и не жалеть на это времени, чем решить несколько однотипных задач одним и тем же способом, закрепляя при этом схему решения задачи предложенным способом без глубокого понимания самого смысла задачи. Из различных способов решения одной и той же задачи надо предложить учащимся выбрать наиболее рациональный, простой, приемлемый для данной личности. Урок решения одной задачи помогает каждому ученику найти свою нишу для самовыражения и понимания себя и других.

Учебники «Математика 5 класс» и «Математика 6 класс» под редакцией С.М. Никольского облегчают работу учителя в выборе задач. Разнообразие типов задач в этих учебниках велико. Иногда в одном номере может быть три или четыре задачи. Это дает возможность детям с разными способностями выбрать ту, которая ему по силам в данный момент, и решить ее своим способом. Ситуация успеха поможет потом этому ученику двигаться дальше, вызовет желание приступить к решению более сложной задачи

.

Очень много можно найти задач с творческой составляющей, решение которых примитивно излагается в готовых домашних заданиях. Я часто предлагаю такие задачи своим ученикам. Они решают их своим способом, применяя рисунки или схемы. Любят представлять свои решения на формате А4 используя любой подручный материал для оформления. (смотри Приложение 2)

При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки. Учащийся находит свой собственный способ решения задачи, который ему доступен и понятен. После нахождения очередного метода решения задачи учащийся, как правило, получает большое моральное удовлетворение. Учителю важно поощрять поиск различных способов решения задач, а не стремиться навязывать своё решение.

Очень часто на уроках геометрии в 10 и 11 классах у своих коллег мне приходилось наблюдать, как учитель используя презентацию с готовым чертежом к задаче, навязывал решение, которое излагалось в интернете, при этом особо не вникая в смысл. Такой подход к решению задачи обесценивает урок. Если нет своей собственной работы над условием, нет процесса построения своего собственного чертежа, то задача останется для ученика чужой. При такой схеме урока ученику остается только запомнить алгоритм решения этой задачи. Но такой подход не даст ему в будущем возможность решить даже подобную задачу с измененным условием.

Особо удивляет меня работа экспертов ОГЭ и ЕГЭ, когда учитель проверяет решение ученика строго по критериям, не пытаясь понять ход решения ученика, изложенного в работе, часто сам не вникая в решение проверяемого задания. Это происходит потому, что на уроках учитель сам не привык решать задачи различными способами, не понимает до конца ценности задачи в школьном курсе математики. Данная работа направлена на то, чтобы помочь учителю понять ценность и место задач в математике.

Общие методы решения задач должны стать доступны каждому ученику. Наряду с этим необходимо растить у них умение использовать свои индивидуальные способности при решении задачи, позволяющие решить её ещё проще. Именно отход от шаблона, конкретный анализ условий задачи являются залогом успешного её решения.

Решая с учащимися ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая – помочь ученику решить именно данную задачу, научить его решать задачи, аналогичные или обратные рассматриваемой, не навязывая ему свой алгоритм решения; вторая - так развить способности ученика, чтобы он мог в будущем решить любую задачу школьного курса самостоятельно. Эти две цели, безусловно, связаны между собой, так как, справившись с заданной достаточно трудной для него задачей, учащийся развивает свои способности к решению задач вообще. Уходит страх перед задачей, появляется азарт в преодолении своей неуверенности при столкновении с незнакомым условием.

Диапазон опыта составляет система урок – внеурочная деятельность.

Традиционные и нетрадиционные способы решения текстовых задач.

Обратимся к существующей теории по описанию задачи и методов ее решения.

Математическая задача – это связанный лаконичный рассказ, в котором введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии. Любая текстовая задача состоит из двух частей: условие и вопрос. В условии излагаются сведения об объектах и некоторых величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними. Вопрос задачи – это указание на то, что нужно найти.

Метод решения задачи – это совокупность математических или иных средств, используемых при решении.

В современной методике обучения решению текстовых задач используют следующие основные методы их решения:

практический,

арифметический,

алгебраический,

геометрический,

схематический,

графический,

табличный,

комбинированный.

В различных источниках перечисляется различное количество способов решения. Для меня более приемлем такой вид их систематизации.

При практическом методе основным средством решения является выполнение практических действий с объектами, о которых идет речь в задаче. 

В арифметическом способе решить задачу – это значит выполнить арифметические действия над числовыми данными из условия задачи, составив числовое выражение, и записать конечный результат вычислений – ответ на вопрос задачи

Очень часто смешиваются понятия способа решения задачи и формы записи решения задачи. В начальных классах используются различные формы записи решения задач: по действиям без пояснения; по действиям с пояснениями; по действиям с вопросами; составлением числового выражения. Но это лишь различные формы записи арифметического способа.

При алгебраическом методе основное средство решения задачи - составление и решение уравнения, системы уравнений или неравенства.

При решении задачи алгебраическим способом необходимо выполнить несколько этапов:

1) Арифметическая краткая запись условия задачи. Цель этого этапа -осмысление задачи и выяснение связей между величинами. Форма записи может быть различной – схематический чертёж или таблица всех известных и неизвестных данных задачи. Важно помнить, что этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями. Однако его наличие свидетельствует о том, что учащийся вник в задачу. Неизвестные величины на чертеже или в таблице удобно обозначать знаком «?», а главный вопрос задачи, например, выделить в «кружок». Нужно помнить, что единицы измерения всех величин должны быть единые. Намного облегчает решение задачи общепринятые обозначения в математике, физике и т.д.

2) Алгебраическая краткая запись условий задачи. Цель этапа – удачно выбрать переменную и выразить все неизвестные величины задачи через неё. Форма записи такая, как и на 1 этапе, но только вместо знаков «?» везде надо записать выражения с переменной. Важно помнить, обычно этот этап начинается с фразы: «Пусть x единиц -…, тогда…». Чаще всего за неизвестное принимают главный вопрос задачи, хотя бывает это и неудобно, тогда за неизвестное принимают наименьшую величину, либо другую величину, благодаря которой можно составить простое уравнение, а затем уже ответить на вопрос задачи. При введении переменной необходимо учесть наибольшее удобство математической записи условия задачи. Многие не понимают ценность этого этапа. Я считаю, что во время этой работы идет формирование математической речи и логической аргументации, происходит процесс тесного «сближения» с задачей, результатом которого является отыскание рационального способа решения.

3) Составление и решение уравнения или системы уравнений, или неравенства. Цель этого этапа – составить уравнение или неравенство, опираясь на условие задачи, и найти его решение. Необходимо учитывать область допустимых значений переменных (ОДЗ), чтобы составить уравнение, нужно увязать известные и неизвестные данные задачи в формулы.

4) Анализ решения уравнения или неравенства. Цель этапа – из всех найденных решений уравнения выбрать те, которые подходят по смыслу задачи. Обычно этот этап начинается фразой: «По смыслу задачи x должна быть величиной…» (положительной, натуральной, целой, принадлежащей промежутку и т.д.) Если смысловое значение не выполнено, то найденную величину называют посторонним решением. Полезно провести проверку.

5) Запись ответа в соответствии с вопросом задачи

Решить задачу геометрическим методом - значит найти ответ на требование задачи, используя геометрические построения или свойства геометрических фигур.

Геометрический способ заключается в применении свойств геометрических фигур и взаимосвязи их элементов в процессе решения задачи. Данный метод делает решение текстовой задачи более наглядным и позволяет избежать громоздких вычислений. Для составления математической модели текстовой задачи чаще всего применяются отрезки и их длины, а также прямоугольники и их площади. Геометрия придает алгебре необыкновенную красоту и изящность. А вместе алгебра и геометрия представляют собой единое целое.

Французский математик София Жермен писала: «Алгебра – не что иное, как записанная в символах геометрия, а геометрия – это просто алгебра, воплощенная в фигурах»

Геометрический метод в решении текстовых задач отличается быстротой выполнения. Очень часто задачи на части, на проценты, движение и совместную работу можно решать с помощью геометрии. И такое решение является неординарным и рациональным, а также позволяет экономить время и быстро находить правильный ответ. Геометрический способ, на мой взгляд, наиболее наглядно позволяет увидеть решение.

Решить задачу схематическим способом - это значит найти ответ на требование задачи, как правило, с помощью схем.

Схематический способ решения задач - это старинный способ, его знали ещё до н.э. в Древней Греции во времена Пифагора, а в 18-19 веках успешно использовали купцы при торговле смешанным товаром. Этот способ решения текстовых задач значительно упрощает решение задач на смешивание растворов и получение сплавов.

Решить задачу графическим способом - значит решить задачу с помощью графиков в прямоугольной системе координат.

Графическое изображение, описывающее условие задачи позволяет наглядно представить ситуацию, описанную в задаче. Также он позволяет находить и составлять новые уравнения, описывающие условие задачи, а иногда и просто заменить алгебраическое решение чисто геометрическим. Особенно успешно можно применять этот метод при решении задач с параметрами в ЕГЭ.

Решение задач табличным способом может существенно сэкономить время, затраченное на оформление и пояснения к действиям, тем более многие задачи можно решить «не выходя» из таблицы. Главное достоинство этого метода – наглядность.

Текстовые задачи на смеси и сплавы, на совместную работу удобнее решать табличным способом. В таблице прописываем формулу, необходимую для расчетов, и придерживаемся главного правила таблицы – если есть две известные величины, то обязательно находим третью. Уместно его использовать при решении экономических задач в ЕГЭ,

При комбинированном методе в процессе решения задачи используются одновременно несколько различных методов решения.

Способ решения задачи – это содержание отношений между данными и искомыми, которые положены в основу решения, и последовательность их использования.

Задача считается решенной различными способами, если ее решения отличаются связями между данными, положенными в основу решений, или последовательностью использования этих связей.

Традиционными способами решения задач являются арифметический и алгебраический, остальные менее известны и редко используемы в школе.

Рассматривая различные источники и анализируя литературу, мы понимаем, что алгебраические задачи можно решать геометрическим, схематическим, графическим, а также табличным способом. Конечно, алгебраический способ - универсальный, но знание различных способов часто упрощает решение задачи.

На основе знакомства с различными способами учащийся сам выбирает удобный понятный и простой для себя способ.

Мои учащиеся в основном используют комбинированный способ решения задач, который является смесью арифметического, схематического и геометрического. Причем в некоторых задачах у одних учеников доминирует геометрический, у других арифметический. Геометрический способ, по мнению моих учеников. является рациональным. Они ценят его за наглядность и быстроту решения. Но не всегда получается решить задачу именно таким способом.

В Приложениях 1,2,3,4 изложены методические приемы и примеры решения задач различными способами моими учениками по учебнику «Математика 5 класс» под редакцией С.М.Никольского.

Результативность

Умение решать задачи является одним из основных показателей уровня математического развития, глубины усвоения пройденного учебного материала.

Систематическое проведение уроков, на которых рассматривается решение одной задачи несколькими способами, формирует у моих учащихся познавательный интерес, самостоятельность и развивает их творческий потенциал. В результате проведения серии таких уроков создаются условия для развития творческой активности, импровизации, неординарности мышления учащихся. При этом процесс познания становится живым делом, а не монотонной работой по заучиванию скучных правил и теорем. Следовательно, обучение математике становится не самоцелью, а средством на пути совершенствования личности.

Основным критерием результативности является степень творческой самореализации школьников в учебно-познавательной деятельности.

Проводимая диагностика оценки познавательной самостоятельности обучающихся, творческой активности и развитости творческого мышления позволяет сделать выводы о положительной динамике показателей. Особенно приятно бывает увидеть это при решении последних нестандартных заданий ВПР по математике.

Данные мониторинга динамики степени проявления показателей творческой активности свидетельствуют об эффективности проведения таких уроков, их положительном влиянии на остальные характеристики уровня творческого развития. Данный подход показывает свою эффективность. Обучающиеся не только развивают творческую активность, но и достигают хороших результатов при написании контрольных, выполнении лабораторных работ по геометрии, с интересом готовятся к школьным и городским конкурсам и с большим желаниям участвуют в них.

Опыт практической работы, направленной на общее развитие, показал мне, что главное достоинство изучения математики заключается в пристальном внимании к развитию творческого потенциала каждого ученика, в соединении репродуктивной и продуктивной деятельности школьников.

Особенно удачной мне представляется система работы учителя и ученика с текстовыми задачами, которая позволяет сформировать у самого учителя и у каждого ученика полноценное умение решать такие задачи не за счет "натаскивания" на основе ранней типизации задач и большого числа их, а за счет разнообразной творческой деятельности каждого ученика.

Учебник «Математика 5» под редакцией С.М. Никольского обладает огромным и разнообразным материалом для различного рода работ над задачей:

• изменение вопроса так, чтобы действий в решении стало больше (меньше);

• изменение условия так, чтобы действий в решении стало больше (меньше);

• изменение вопроса (условия, данных) так, чтобы задача стала нерешаемой;

• внесение в задачу таких изменений, чтобы в ней появились лишние (недостающие) данные;

• внесение в задачу таких изменений, чтобы в ней исчезли лишние (недостающие) данные;

• изменение текста задачи так, чтобы в ее решении появилось обратное действие.

Это можно рассмотреть на задаче № 561 в Приложении 3.

Материал для такого вида деятельности можно найти в этом учебнике в заданиях под заголовком «Придумываем задачу», «Исследуем», «Занимательные задачи», «Доказываем». В разделе «Дополнения к главе» помещено такое разнообразие задач, на котором легко можно отработать все способы решения задач.

Помимо заданий, требующих преобразований текстов задач, большое внимание уделяется:

• подбору и самостоятельному составлению обратных задач;

• сравнению задач с одинаковой фабулой, но различным математическим содержанием;

• сравнению задач с разной фабулой и одинаковым математическим содержанием.

Постоянное использование всех этих аспектов работы с задачами дает хорошие результаты, способствует формированию умения решать задачи. К сожалению, значительно меньшее внимание авторы учебников уделяют решению задач разными способами. Число таких заданий значительно меньше, они встречаются от случая к случаю и в силу этого не воспринимаются многими учителями как важные.

Необходимо отметить, что решение задач разными способами – чрезвычайно увлекательное занятие для учащихся различных возрастных групп. Интерес, любопытство, творчество, желание добиться успеха – это привлекательные стороны, которые позволяют учащимся любить и выбирать этот вид деятельности на уроках математики

А вот доводы в пользу постоянного решения задач разными способами с позиции учителя: этот вид деятельности способствует интенсивному развитию логического мышления, его глубины и гибкости, создает условия для улучшения речи учащихся (точности произношения и употребления слов, яркости и динамичности), готовит базу для решения задач разными способами в основной школе по разным предметам; способствует осуществлению личностно-ориентированного подхода, адаптации школьников, гуманизации обучения – важнейшей проблемы современной школы.

Решение задачи разными способами гарантирует право ученика на выбор решения, даже если оно не является традиционным, у него появляется дополнительная возможность справиться с делом. Выбор при нахождении решения задачи, вариантов ее оформления делает ученика свободным, спокойным, появляется возможность достичь успеха, возникает устойчивость важной для жизни мысли: "Всегда можно найти выход из сложной ситуации". А это является важной составляющей частью формирования социально адаптированной личности в условиях современной школы.

Заинтересованность учителя в данном виде деятельности плюс игра, поиск, азарт, воображение учащихся убеждают меня в том, что необходимо постоянно решать задачи разными способами.

Овладевая несколькими способами решения задачи, ученик учится быстро и рационально решать задачи и начинает увереннее себя чувствовать на уроках математики. Из существующих способов учащийся сам осуществляется выбор рационального способа решения. Он определяет, как рациональнее решать задачу – арифметически, алгебраически или частично так, а частично так. После сделанного выбора ученик аргументировано доказывает рациональность конкретного предложенного им решения

Рациональный (лат.) – разумный, целесообразный. При решении рациональным способом числа подбираются так, чтобы с ними было удобно проводить математические операции, или само решение выполняется меньшим числом действий. Но слово «рациональный» не следует соотносить со словом «легкий», так как довольно часто бывает, что учащимся легче решить задачу большим числом действий.

Перед решением задачи возможно использовать следующие формы ее записи, если это необходимо ученикам:

• краткую запись с использованием общепринятых условных обозначений (вот аргумент в ее защиту: требует внимательного чтения текста задачи, «дисциплинирует» числа, позволяет установить взаимосвязь между величинами);

• графическое моделирование задачи;

• таблицу;

• схематическое моделирование;

• рисунок;

• предметное моделирование.

В случае необходимости при поиске разных способов решения задачи ученикам предлагаются разные формы помощи (особенно важную роль играет помощь в начале приобщения детей к такому виду деятельности).

Для реализации развития познавательной и творческой активности школьника в учебном процессе используются современные образовательные технологии, дающие возможность повышать качество образования, более эффективно использовать учебное время и снижать долю репродуктивной деятельности учащихся за счет снижения времени, отведенного на выполнение домашнего задания.

Слово «технология» происходит от греческого слова: «techne» - искусство, мастерство, умение и «logos» - наука, закон. Дословно «технология» - наука о мастерстве. Инновационные педагогические технологии взаимосвязаны, взаимообусловлены и составляют определенную дидактическую систему, направленную на воспитание таких ценностей, как открытость, честность, доброжелательность, сопереживание, взаимопомощь и обеспечивающую образовательные потребности каждого ученика в соответствии с его индивидуальными особенностями.

Решение задач разными способами отвечает требованиям следующих современных педагогических технологий:1) Проблемное обучение (создание в учебной деятельности проблемных ситуаций и организация активной самостоятельной деятельности учащихся по их разрешению, в результате чего происходит творческое овладение знаниями, умениями, навыками, развиваются мыслительные способности); 2) Разноуровневое обучение (у учителя появляется возможность помогать слабому, уделять внимание сильному, реализуется желание сильных учащихся быстрее и глубже продвигаться в образовании, сильные учащиеся утверждаются в своих способностях, слабые получают возможность испытывать учебный успех, повышается уровень мотивации обучения); 3) Исследовательский метод в обучении (дает возможность учащимся самостоятельно пополнять свои знания, глубоко вникать в изучаемую проблему и предлагать пути ее решения, что важно при формировании мировоззрения и для определения индивидуальной траектории развития каждого школьника); 4) Технология использования в обучении игровых методов: ролевых, деловых и других видов обучающих игр (расширение кругозора, развитие познавательной деятельности, формирование определенных умений и навыков, необходимых в практической деятельности, развитие обще-учебных умений и навыков);

5) Обучение в сотрудничестве (сотрудничество трактуется как идея совместной развивающей деятельности взрослых и детей, суть индивидуального подхода в том, чтобы идти не от учебного предмета, а от ребенка к предмету, идти от тех возможностей, которыми располагает ребенок, применять психолого-педагогические диагностики личности).

Сегодня под проблемным обучением понимается такая организация учебных занятий, которая предполагает создание под руководством учителя проблемных ситуаций и активную самостоятельную деятельность учащихся по их разрешению, в результате чего и происходит творческое овладение профессиональными знаниями, навыками, умениями и развитие мыслительных способностей. Целью проблемной технологии выступает приобретение ЗУН, усвоение способов самостоятельной деятельности, развитие познавательных и творческих способностей. Проблемное обучение основано на создании особого вида мотивации – проблемной, поэтому требует адекватного конструирования дидактического содержания материала, который должен быть представлен как цепь проблемных ситуаций. Проблемные методы – это методы, основанные на создании проблемных ситуаций, активной познавательной деятельности учащихся, состоящей в поиске и решении сложных вопросов, требующих актуализации знаний, анализа, умения видеть за отдельными фактами явление, закон. В современной теории проблемного обучения различают два вида проблемных ситуаций: психологическую и педагогическую. Первая касается деятельности учеников, вторая представляет организацию учебного процесса. Педагогическая проблемная ситуация создается с помощью активизирующих действий, вопросов педагога, подчеркивающих новизну, важность, красоту и другие отличительные качества объекта познания. Создание психологической проблемной ситуации сугубо индивидуально. Ни слишком трудная, ни слишком легкая познавательная задача не создают проблемной ситуации для детей. Проблемные ситуации могут создаваться на всех этапах процесса обучения: при объяснении материала, закреплении, контроле знаний.

Решение текстовых задач разными способами отвечает всем требованиям современных педагогических технологий.

Предлагаю примерный план хода урока одной задачи. На уроке при решении задачи различными способами учитель ставит следующую проблему учащимся. Он предлагает решить какую-нибудь задачу разными способами. Ученики самостоятельно читают задачу несколько раз. Потом кто-нибудь из них придумывает вопрос, на основании которого можно будет выявить, понято ли условие или нет, затем учитель может задать свои вопросы по выявлению уровня понимания условия задачи. Затем учащиеся могут задать вопросы учителю по тем затруднениям, которые возникли у них в процессе изучения условия задачи.

Когда заканчивается работа над изучением и пониманием условия, приступаем к решению задачи. К доске выходят 3-4 ученика, которые начинают решать задачу своим рациональным индивидуальным способом. Иногда способы решения задачи могут совпасть. Это не страшно. Кто-то может в тетради решить задачу другим удобным и простым способом. Потом начинается защита своего решения. Ученик начинает доказывать рациональность использования своего способа решения. Иногда в процессе такой работы учащийся находит минусы и плюсы своего или чужого способа. Такая работа проходит в духе соревнования. Часто ученики могут ощутить поддержку своих товарищей. Они пытаются помочь отвечающему аргументировано доказать свою правоту. Многие начинают видеть простоту и доступность хода решения одноклассника и благодарят его за то, что он открыл им простой и доступный путь решения данной задачи, о котором они даже не подозревали

Учителю очень важно тщательно продумать ход такого урока, придумать каверзные вопросы по условию, ответы на которые позволят ученику детально вникнуть в понимание условия задачи и найти самому различные способы решения данной задачи. Всегда после таких уроков учитель сам приобретает неоценимый опыт. Иногда ученик выдает такой способ решения задачи, о котором учитель даже не подозревал. Часто после такого урока учитель выявляет недостатки в обучении своих учащихся, что позволит в дальнейшем скорректировать его работу.

Заключение.

 Таким образом, решение задачи различными способами требует применение комплекса ранее полученных знаний. А, значит, это процесс систематизации усвоенных учащимися знаний и умений. К тому же при решении задачи различными способами у ученика формируется умение анализировать прочитанное, правильно оформлять свои записи, письменные работы.

«Хороший учитель обязан понимать, что никакую задачу нельзя исчерпать до конца. Этот взгляд он должен прививать и своим ученикам.» (Д. Пойа). 

 На уроках при решении одной задачи различными способами данная задача выступает уже не только в качестве иллюстрации теории, а рассматривается и как самостоятельный объект, как средство развития исследовательской деятельности учащихся. Поиск различных способов решения, критическая оценка этих способов с целью выделения из них наиболее рационального – важный фактор развития математического мышления. При этом прежде всего развивается гибкость (нешаблонность) ума, которая проявляется в быстроте ориентировки в новых условиях, в умении видеть новое в известном, выделять существенное, выступающее в скрытой форме. Нельзя не учитывать и того, что решение задачи различными способами развивает навыки самоконтроля у учащихся, поскольку ответ при всех найденных способах решения одной задачи должен быть одинаков.

Решение задачи различными способами – это увлекательный творческий процесс, развивающий воображение, подталкивающий учащегося придумывать, искать все новые и новые способы решения задачи.

Если говорить о дидактических функциях излагаемого материала, то здесь следует отметить вводно-мотивационную и контрольно-оценочную. Систематизация знаний, формирование обще-учебных умений, развитие математического мышления, навыков самоконтроля, самостоятельности в отыскании путей решения являются главными при обучении математике. Наконец, налицо и воспитательные функции – воспитание личностных качеств школьников (трудолюбия, целеустремлённости, настойчивости, аккуратности, сотрудничества), культивтрования интереса к изучаемому предмету.

Опыт работы в школе показывает, что решение одной и той же задачи различными методами естественно вписывается в процесс проведения урока по решению задач. Систематическое применение этого приёма даёт значительный эффект как при обучении решению задач по геометрии, так и при обучении курсу математики в целом. Обучение математике необходимо не только для того, чтобы учащиеся овладели определённой суммой знаний, но и для того, чтобы эти знания они могли эффективно использовать для решения разнообразных задач, возникающих в практической деятельности.

Обобщим выявленную ценность задач, имеющих несколько способов решения.

В целях совершенствования преподавания математики необходимо использовать уроки решения одной задачи, однако увлекаться этой формой не следует. Такие уроки станут наиболее эффективными, если их проводить один или два раза в месяц. Тогда можно подобрать такую задачу, при решении которой действительно применялся бы большой объём изучаемого материала.

Рекомендуется систематически использовать на уроках задачи, способствующие формированию у учащихся познавательного интереса, самостоятельности и развитию индивидуального творческого потенциала.

Как можно чаще надо задавать для домашнего задания задачи, предлагаемые учебником «Математика 5 класс» и «Математика 6 класс» под редакцией С.М.Никольского, в процессе решения, которых учащийся использует свой собственный наглядный вариант решения задачи или предлагает несколько способов решения задачи, используя свободный стиль изложения и краткой записи, и решения задачи, что повышает самостоятельность и развивает творческий потенциал ученика. Некоторые учащиеся с неохотой принимают такой подход к решению задачи. Они хотят выучить алгоритм, не вникая в смысл, и строго следовать ему. В этом случае учителю надо иметь терпение к таким ученикам. Любая проверочная работа покажет, что такой подход к решению задачи не приносит результатов. Зачастую каждый из нас слышал фразу недовольства «А мы такое не решали!»

Учителю приходится объяснять, что невозможно в огромном количестве задач работать по алгоритмам. В любую задачу следует сначала вникнуть, а потом начать поиск своего решения, который приведет к успеху, но для этого следует решать различные задачи, не привязываясь к алгоритму. Это долгий и кропотливый процесс.

Осуществление целенаправленного обучения школьников решению задач с помощью специально подобранных упражнений учит их наблюдать, пользоваться синтезом, индукцией, сравнениями и совершенствовать навыки смыслового чтения.

Целесообразно использовать на уроках задачи на сообразительность, задачи-шутки, математические ребусы, софизмы.

Надо учитывать индивидуальные особенности школьника, дифференциацию познавательных процессов у каждого из них, используя задания различного типа, практикуя решения задач различными способами.

«Если ученик в школе не научился творить, то в жизни он будет только подражать и копировать». Л.Н. Толстой

В записях Жан Дьедоне можно прочитать: «В конце концов, к каким целям стремятся в нашем цивилизованном мире, преподавая детям математику? Конечно, не к тому, чтобы познакомить их с определенным числом более или менее остроумных теорем о биссектрисе треугольника или о последовательностях простых чисел, которым они не найдут ни малейшего применения (по крайней мере, они не станут профессиональными математиками), но для того, чтобы научить их приказывать своим мыслям и управлять ими по методу, которым пользуются математики, а также потому, что эти упражнения являются прекрасным средством развития ясности ума и строгости суждений. Именно эта сущность математического метода должна стать основой преподавания, а преподаваемый материал представляться лишь хорошо подобранной иллюстрацией».

В заключение хочется отметить, что работа учителя – это постоянный поиск себя, развитие своего творчества, поэтому каждый выбирает свои методы, пользуется своими индивидуальными приёмами

Я поделилась с Вами методическими разработками по решению задач различными способами, которые находятся в приложениях 1,2,3,4, взглядами на педагогику и методику преподавания математики, используя психологию и философию. Я считаю, что математика-царица всех наук. Только она позволяет научиться жить нам осмысленно, только она может развить нашу логику и абстрактное мышление, только она может заставить нас думать и находить выход из любой трудной ситуации, встретившейся нам в реальной жизни, только она позволяет нам гармонично существовать и развиваться в окружающем нас мире, только с помощью нее можно осуществлять открытия и прорывы в науках. Помните, что мы - существа разумные. А развить наш разум и логику можно только с помощью обучения такой трудной и одновременно легкой особенности нашего мозга, как умение думать, где главное место в развитии этой особенности принадлежит математике.

Список использованной литературы

Учебники, статьи.

1. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика 5 класс. – Москва: Просвещение, 2018.

2. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В. Математика 6 класс – Москва: Просвещение, 2018.

3. Капкаева Л.С. Алгебраический и геометрический методы в обучении математике. Математика в школе. Научно-теоретический и методический журнал. №7 – М.: Издательство ООО «Школьная пресса» 2004.

4. Классен Н.В. Современные технологии в образовательной системе. Образование, инновации, исследования как ресурс развития сообществ: материалы научно-практическая конференция (Чебоксары, 18.12.17 г.) – Чебоксары: ИД «Среда», 2017.

5. Раимбекова Г.К. Современные технологии в школьном образовании Педагогика общеобразовательной школы: Материалы VIII Международная научно-практическая конференция. Краснодар: Новация, 2016.

6. Еркин С.Л. Современные образовательные технологии. Москва. ООО Издательская Группа «Основа» 01.04.2019

7. Абрамов А.А. Методы решения текстовых задач. https://school-science.ru/6/7/36427 2019

8. Айвазян Н.С. Статья «Этапы, методы и способы решения задач» - ‎2017 https://cyberleninka.ru/article/n/etapy-metody-i-sposoby-resheniya-tekstovyh-zadach-nachalnogo-kursa-matematiki/viewer

9. Муштавинская И.В., Крылова О.Н., Даутова О.Б. «Лучшие практики введения и реализации ФГОС общего образования: сборник статей Межрегиональной научно-практической конференции» - СПб АППО, 2015. – (Федеральный государственный образовательный стандарт) – ISBN 978-5-7434-0738-0

10. Патрикова Т.С. Готовая карта педагогических технологий, чтобы ученики достигали результатов по ФГОС на каждом уроке // Справочник заместителя директора школы. – 2018. - №10.

11. 11.Решение задач различными способами https://sites.google.com/site/razinova59/home/iz-opyta-raboty/resenie-zadac-razlicnymi-sposobami

12. Дендюк Л. Решение текстовых математических задач разными способами в системе развивающего обучения Л.В. Занкова –Журнал Начальная школа № 5 2003 https://nsc.1sept.ru/article.php?ID=200300504

13. Творческие работы учащихся МБОУ гимназии № 4, 2017-2019

Приложение 1.

Тема: Задачи на нахождение двух чисел по их сумме и разности (п.1.17)

Перед рассмотрением этой темы в учебнике «Математика 5» под редакцией С.М. Никольского изучается тема «Задачи на части» (п.1.14). Во время изложения этой темы автор учебника сначала рассматривает задачи, в которых явно упоминаются части, то есть равные некоторые величины. Такие задачи обычно предлагается решить с помощью простых рассуждений. Хотя по другому учебнику для 5 класса такой тип задач рекомендуют решать с помощью уравнения. Я вместе со своими учениками разбирала текст учебника, в котором излагалось решение задачи с помощью цепочки рассуждений. В учебнике на стр.48 была иллюстрация к этой задаче. После трех-пяти раз вдумчивого чтения текста учебника смысл задачи и ее решение поняли только самые сильные ученики (10 % класса). Но когда я изменила условие задачи и предложила самостоятельно провести такие же рассуждения, то процент понимания и осмысления стал еще ниже. Я поняла, что многие из учеников на первом этапе просто запомнили алгоритм решения. Но это не помогло при решении другой задачи.

Затем в учебнике излагается решение такого же типа задачи, но уже и использованием схематического рисунка. Я называю этот способ решения задачи с помощью отрезков. При изложении этого материала самое главное, что должен понять ученик, заключается в том, что, когда решаешь задачи таким способом, надо понимать, что выбранная часть при изображении схемы должна быть одного и того же размера. Этот отрезок, с помощью которого мы изображаем одну часть, называется единичным. Я предлагала его размер выбирать от двух до пяти клеток. Во время решения некоторого количества такого рода задач каждый ученик выбирает оптимальный для себя размер единичного отрезка. Вырабатывается понимание того, что детальное изучение условия задачи само подталкивает к выбору размера единичного отрезка.

Потом мы решили эту же задачу в отрезках. Наглядность изображения вызвала восхищение более половины учащихся. Во время такого изложения решения произошло полное осмысление и условия задачи, и его решения.

После решения десятка задач таким способом у каждого ученика появился свой собственный симбиоз-способ, к котором соединяется и схема, и рассуждение, который в методической литературе называется комбинированным или смешанным.

Я предлагаю самое понятные и простые решения задач № 288 и № 290, по мнению учеников 5 А класса, где схема и рассуждение приводят к наглядному и простому решению.

Задача № 288 (стр.62 «Математика 5» под редакцией С.М. Никольского)

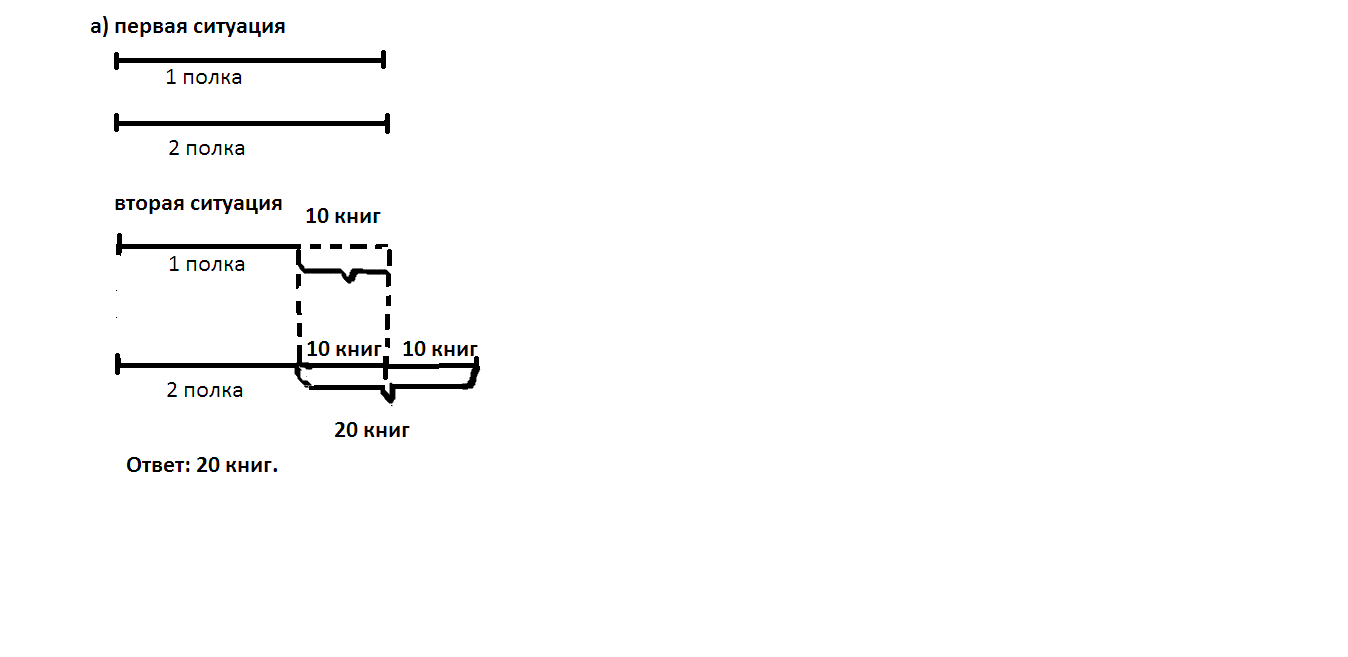
а) На двух полках книг было поровну. С первой полки переставили 10 книг на вторую полку. На сколько книг на второй полке стало больше, чем на первой?

рис.1

б) В первой пачке на 30 тетрадей больше, чем во второй. Сколько тетрадей надо переложить из первой пачки во вторую, чтобы уравнять число тетрадей в пачках?

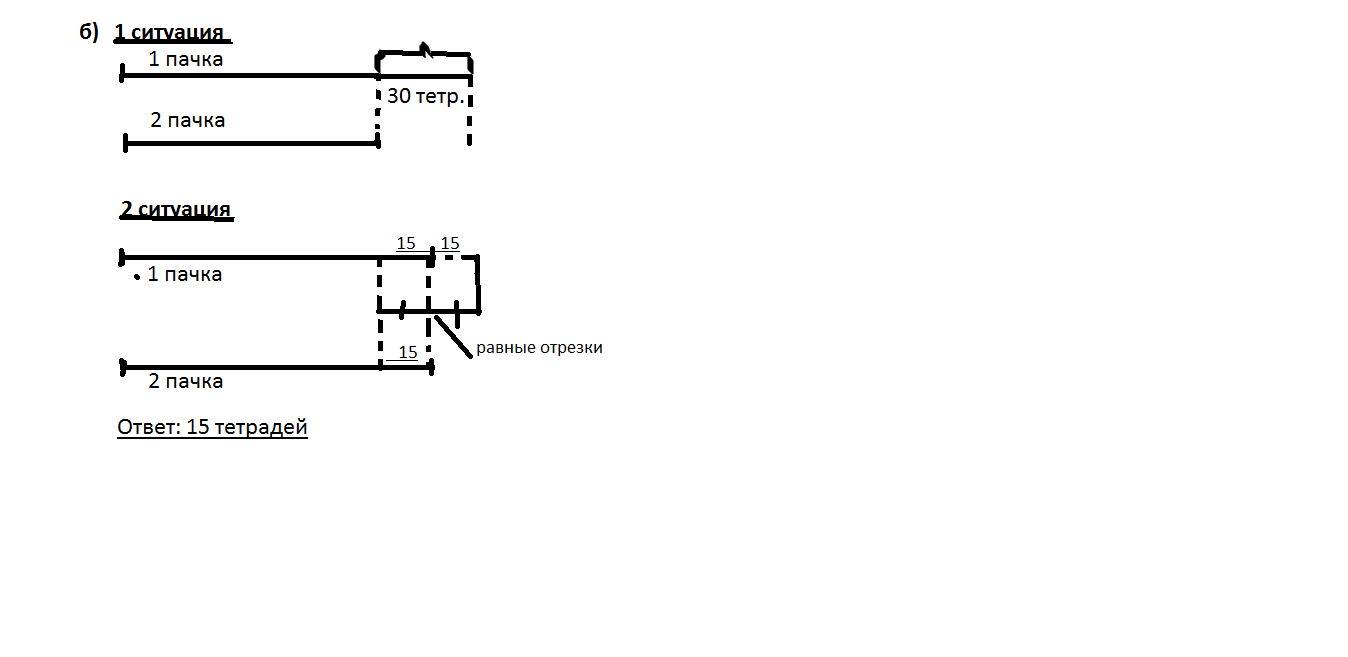
рис.2

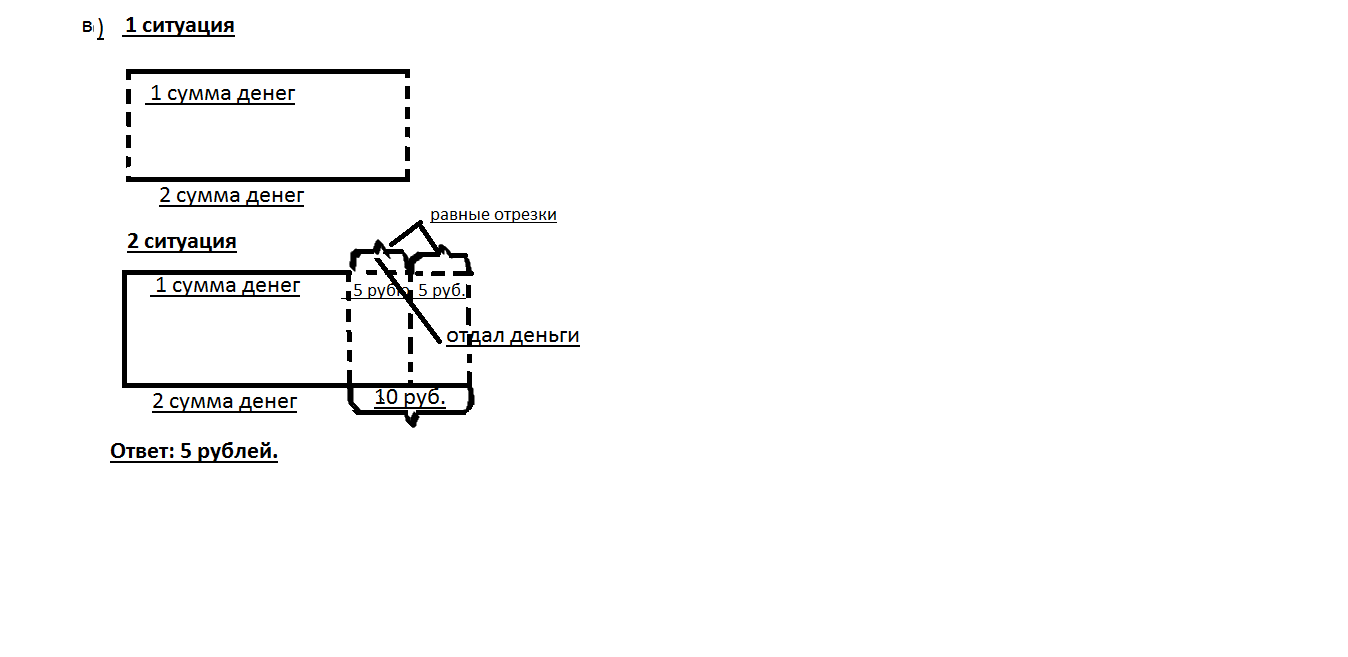
style="position: absolute; top: 0.96in; left: 1.39in" в) Предположим, что у вас и у меня имеется одинаковая сумма денег. Сколько денег я должен вам дать, чтобы у вас стало на 10 рублей больше, чем у меня?

рис.3

Задача № 290 (стр.62 «Математика 5» под редакцией С.М. Никольского)

На вопрос учеников о дне своего рождения учитель математики ответил загадкой: «Если сложить день и номер месяца моего рождения, то получится 20; если из дня рождения вычесть номер месяца рождения, то получится 14; если к произведению дня и номера месяца моего рождения прибавить 1900, то получится год моего рождения». Когда родился учитель математики?

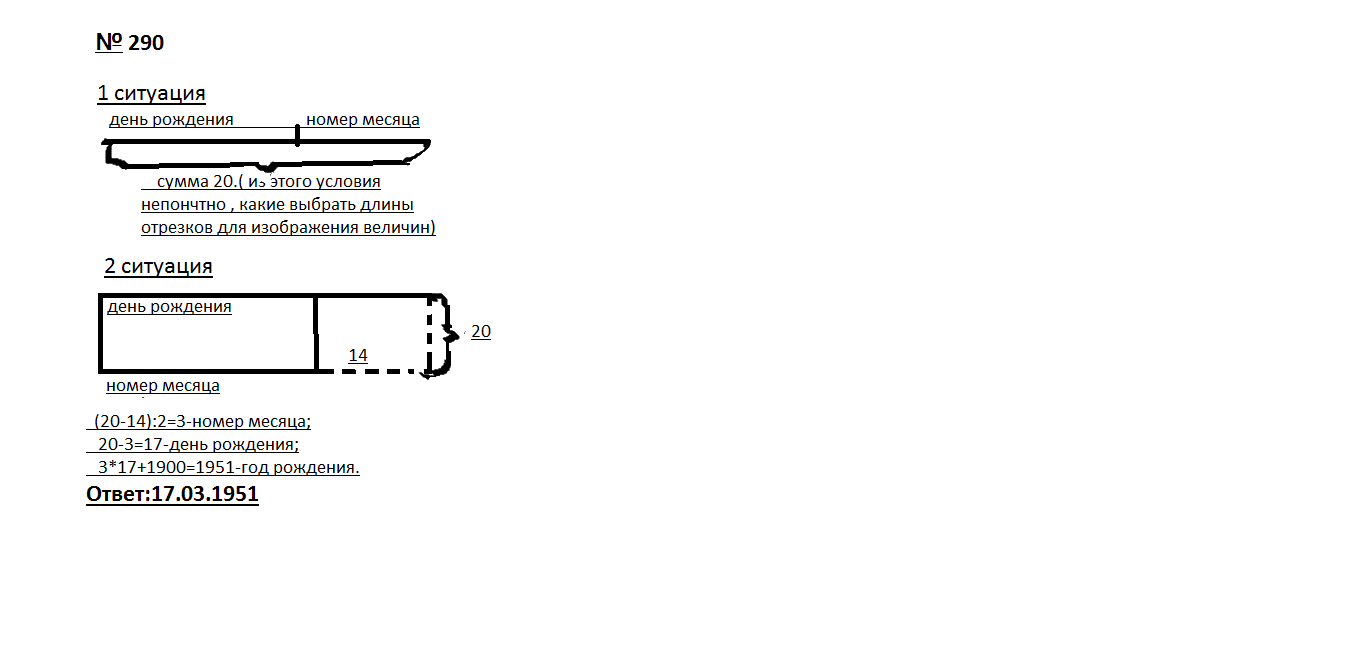
рис.4

Приложение 2.

Тема: Применение смешанного комбинированного способа решения для задач с обыкновенными дробями.

Мои ученики любят творческие задания. Учебники под редакцией С.М.Никольского имеют огромное количество материала для этого. Учащиеся с огромным желанием любят на формате А4 оформлять решение задач повышенной трудности. Они имеют свободу выбора любого способа, который рождается у ученика во время решения задачи. Половина учащихся выполняют решение этих задач смешанным способом, то есть тем, который им более понятен. Ранее мне приходилось на уроке разбирать задания повышенной трудности из контрольных работ. После решения десятка сложных задач понятными и доступными им способами, я наблюдаю тенденцию самостоятельного подхода к решению такого рода задач повышенной трудности. Проходит боязнь приступить к их решению. Я не ввожу строгое оформление при решении таких задач.

В приложении 2 я привожу решения своих учеников.

№ 860 (стр.191 «Математика 5» под редакцией С.М. Никольского)

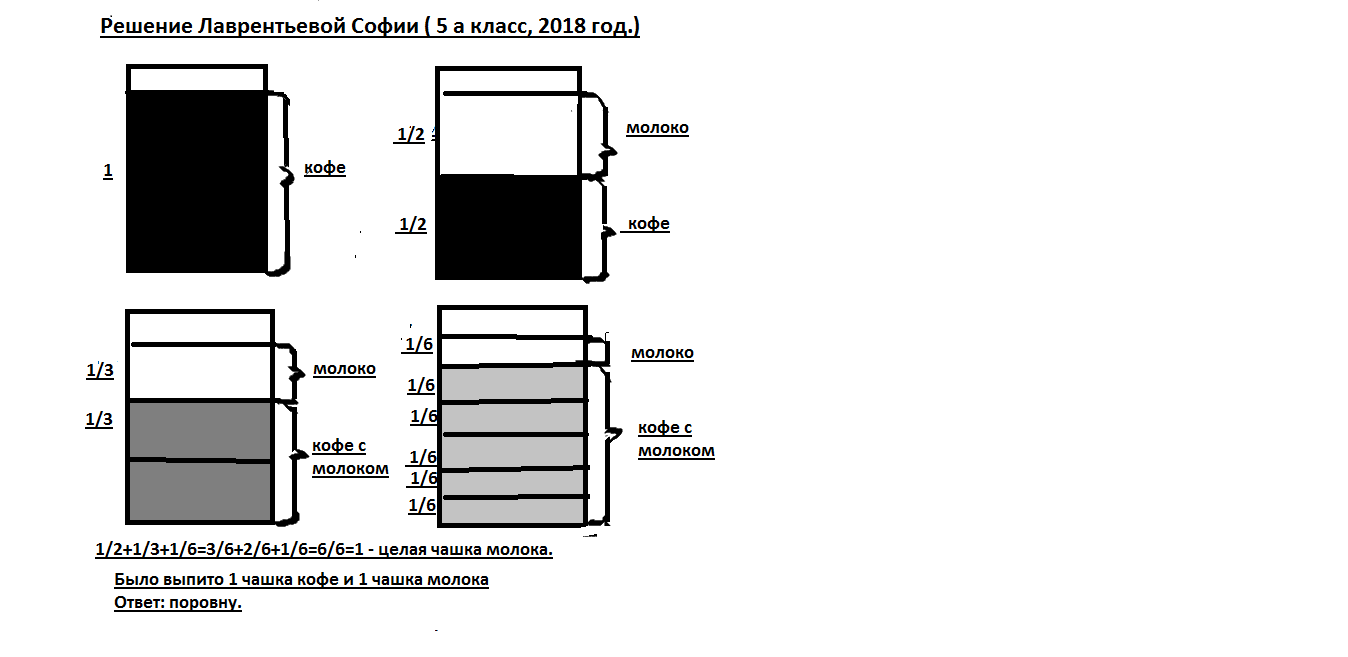
style="position: absolute; top: 1.17in; left: 0.7in" Отпили полчашки черного кофе и долили его молоком. Потом отпили 1/3 чашки и долили ее молоком. Потом отпили 1/6 чашки и долили ее молоком. Наконец допили содержимое чашки до конца. Чего выпили больше: кофе или молока?

рис.5

Решение Исматулаева Хабиба (5 а класс,2018 год)

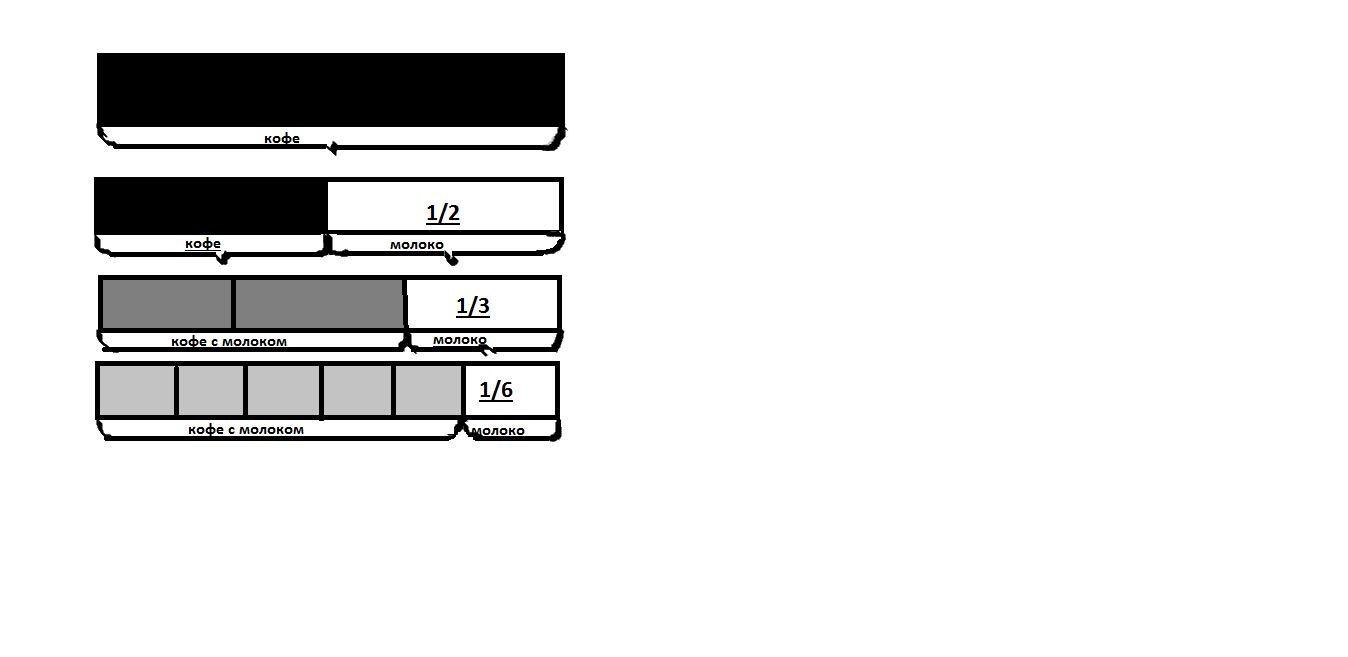
рис.6

1/2+1/3+1/6=3/6+2/6+1/6=6/6=1 чашка молока.

Было выпито поровну кофе и молока

Ответ: поровну.

Приложение 3.

Тема: Задачи на движение.

Особое внимание хочу уделить пункту 2.14. по учебнику «Математика 5 класс» под редакцией С.М.Никольского В практической части пункта собраны различные задачи на движение. Некоторые из них идентичны тем, которые учащиеся будут решать на ОГЭ и ЕГЭ по математике. Как объяснить ученику 5 класса такие сложные задачи? В интернете изложены решения этих задач на таком уровне, которые с трудом будут понятны даже ученику 9 класса.

В теории к п 2.14 очень хорошо и доступно изложен материал, помогающий освоить решение задач на движение по реке. На стр.119 вводятся такие величины как скорость по течению реки и против течения реки. На стр.120 имеется схема, на которой наглядно изображены связь между всеми скоростями, которые появляются в ходе решения задач при движении по реке. Рекомендую перед решением такого типа задач сначала разобрать № 538 устно, где ученики стараются понять связь между скоростями, потом отработать вычислительные навыки нахождения этих скоростей при помощи № 544. Затем очень полезно выполнить № 545. При выполнении этого номера не помогут вычислительные навыки. Здесь на первое место выходит осмысленное понимание связи между величинами при движении по реке. Ответы на вопросы в этом номере помогут вам понять уровень усвоения вашими учениками смысловой связи между величинами в задаче.

В пункте на стр.120 вводятся такие величины при движении, как скорость удаления и скорость сближения.

Но мне кажется, что далее задачи на движение решаются с помощью рассуждений непонятных для учеников 5 класса. Чтобы научить учеников пятого класса решать эти задачи надо:

Во-первых, решить все задачи в том порядке, который автор установил в данном учебнике.

Во-вторых, я думаю, что решение задач с помощью аналитических рассуждений очень сложно для учеников этого возраста, поэтому смешанный способ, по моему мнению, будет самым удачным для решения многих задач на движение. Кроме всего прочего в этих задачах особую сложность вызывают данные задачи, которые заданы в разных единицах измерения. Такой перевод единиц даже в седьмом классе бывает труден для учеников. Кроме этого, ученики пятого класса не умеют еще работать с обыкновенными дробями.

Предлагаю вам рассмотреть решение следующие решения задач различными способами.

Задача № 561 (стр.124 «Математика 5» под редакцией С.М. Никольского)

Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт шляпу. Только через 15 минут папа заметил пропажу. Как далеко друг от друга в этот момент находилась лодка и шляпа, если собственная скорость лодки 8 км/ч, а скорость течения 3 км/ч? Нет ли в задаче лишних данных?

Решение:

В этой задаче скорость измеряется в км/ч, а время в минутах. Можно перевести км/ч в км/мин. Если за час лодка проходит 8 км, тогда за 1 минуту пройдет в 60 раз меньше. В 5 классе до темы обыкновенные дроби ученики не смогут разделить 80 на 60. Если даже км перевести в м, все равно не получим натуральное число. Поэтому при разборе решения этой задачи рекомендуется сначала разобраться в условии задачи, затем спрогнозировать все шаги решения, а уже потом перейти к конкретным числовым значениям.

Sшляпы= V реки х t

Sлодки= V против течения х t = (V собств. - V реки) х t

S между лодкой и шляпой= Sшляпы + S лодки= V реки х t+ (V собств - V реки)хt

При решении по данной формуле прийдется переводить часы в минуты. Но при этом надо будет выполнить непонятные для учеников 5 класса умозаключения. Поэтому при решении этой задачи рекомендуется использовать такое понятие, как скорость удаления.

V удаления= Vсобств.-V реки + V реки = V собств.

S между лодкой и шляпой= V собств. х t

Получается, что значение скорости течения реки лишнее данное в этой задаче.

рис.7

Решение:

V собств. х t= 8:4=2 (км)

15 минут в 4 раза меньше, чем 1 час. Значит если за час лодка проходит 8 км, то за 15 минут проплывет в 4 раза меньше.

Ответ: 2 км

На первый взгляд может показаться, что задача решена. Но если вспомнить, что задача со звездочкой, то стоит задуматься о том, что может есть еще какой-нибудь вариант, который мы пока не обнаружили. Перечитав условие несколько раз, понимаешь, что единственное, что можно изменить это направление движения по реке. Предположим, что папа и сын плывут на лодке по течению реки.

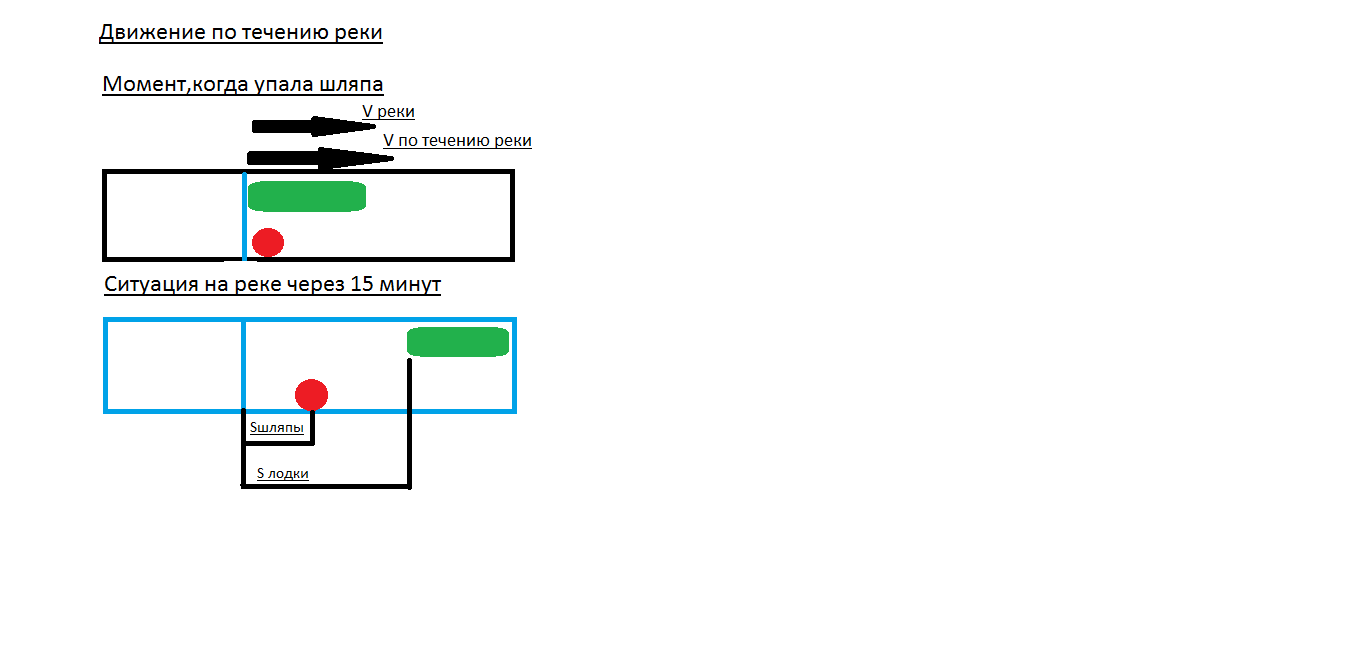
рис.8

Sшляпы= V реки х t

Sлодки= V по течения х t = (V собств. + V реки) х t

S между лодкой и шляпой= Sлодки - S шляпы= (V собств.-+V реки) х t-V реки х t

V удаления= Vсобств.+V реки - V реки = V собств.

S между лодкой и шляпой= V собств. х t

Получается, что значение скорости течения реки лишнее данное.

Кроме всего прочего информация о том, в каком направлении движется лодка по реке, не имеет значение.

Ответ: 2 км; скорость реки и направление движения по реке являются лишними данными.

Задача № 562 (стр.125 «Математика 5» под редакцией С.М. Никольского)

Два поезда движутся навстречу друг другу по параллельным путям-один со скоростью 100 км/ч, другой со скоростью 80 км/ч. Пассажир, сидящий во втором поезде, заметил, что первый поезд шел мимо него 12 с. Какова длина первого поезда?о

Решение:

Эта задача очень трудна для понимания не только в 5 классе, но и для старшеклассников. Я не знала, каким образом просто и наглядно объяснить это ученикам 5 класса. Поэтому решила сначала изменить условие задачи, предположив, что сначала первый поезд едет, а второй стоит, потом изменить это условие на то, что первый стоит, а второй едет. Только потом рассмотреть одновременное движение поездов. Сначала пытаемся решить задачу так, как мне предлагают ученики. Во время этого процесса наталкиваемся на много трудностей. Кто-то вообще не понимает, как приступить к решению, кого-то смущает что скорость измеряется в км/ч, а время в секундах. Мне самой было очень трудно найти Единственное, что приходило на ум – это составить уравнение. Позже появился простой способ решения этой задачи, понятный для учащихся 5 класса. Предлагаю следующий ход решения этой задачи.

Первый этап: Первый поезд стоит, второй едет.

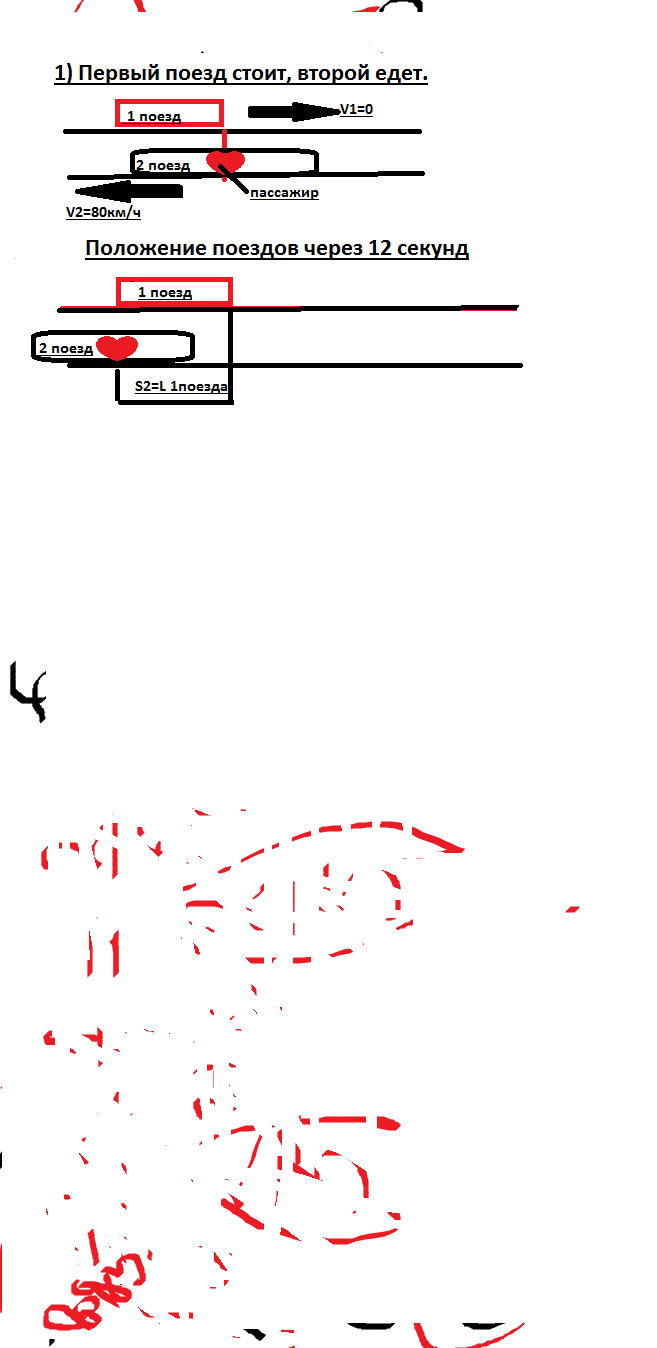
рис.9

Второй этап: Второй поезд стоит, первый едет.

рис.10

Третий этап: Оба поезда движутся по параллельным путям навстречу друг к другу.

рис.11

Решение:

1. 100+80=180 (км/ч) – скорость удаления.

2. 180 км=180000м; 1час=3600 с.; 180000:3600=50 м/с;

3. 50х12=600(м)- длина поезда.

Задача № 563 (стр.125 «Математика 5» под редакцией С.М. Никольского)

Железнодорожный состав длиной 1 км проходит мимо километрового столба за 1 минуту, а через туннель при той же скорости за 3 минуты. Какова длина туннеля?

Сначала рассмотрим ситуацию, когда поезд идет мимо столба.

Решение:

Значит за 1 минуту состав проходит путь, равный своей длине, то есть 1 км.

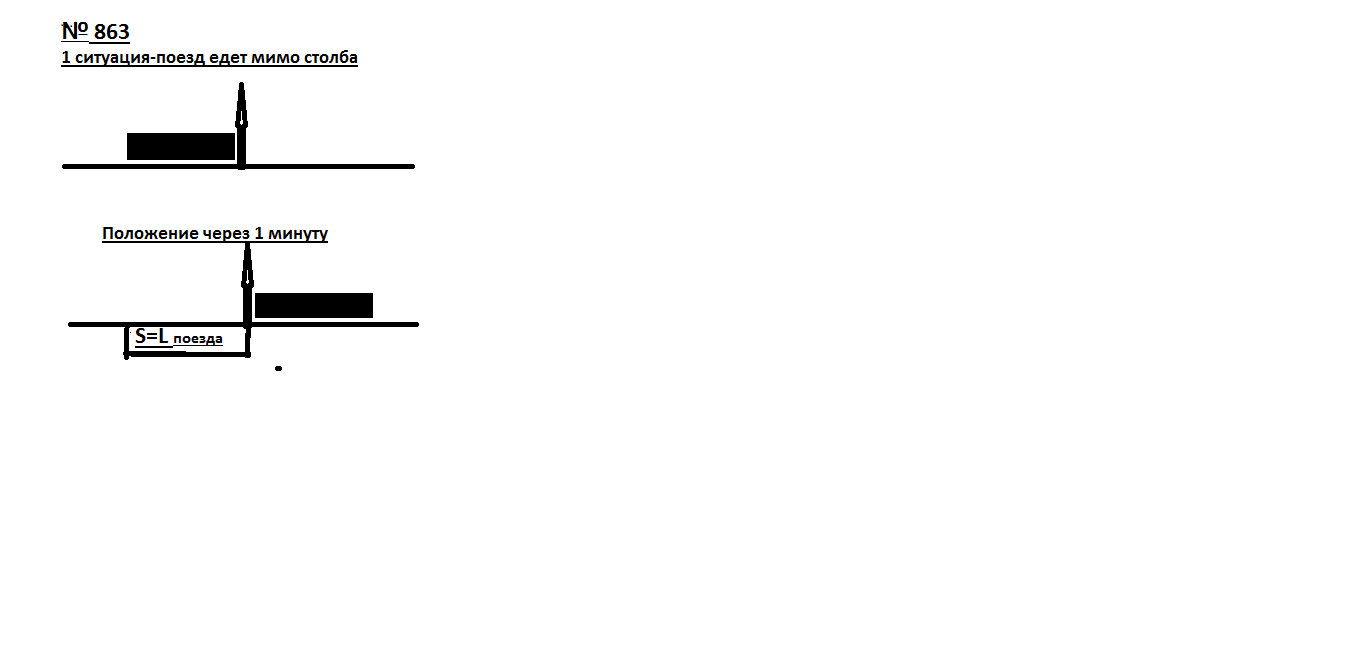
рис.12

Рассмотрим ситуацию, когда поезд проходит туннель. За 3 минуты поезд пройдет путь в 3 раза больше, чем за 1 минуту, то есть 3 км.

L туннеля = S поезда за 3 мин- L поезда = 3км -1 км = 2км

Ответ: 2 км.

рис.12

Задача № 564 (стр.125 «Математика 5» под редакцией С.М. Никольского)

а) Из пункта А в пункт В вышел пешеход со скоростью 5 км/ч. Одновременно с ним из А в В выехал велосипедист со скоростью 10 км/ч. Велосипедист доехал до В, повернул назад и поехал с той же скоростью навстречу пешеходу. Через сколько часов после начала движения они встретятся, если расстояние между А и В 30 км?

Излагаю 3 способа решения этой задачи, которые были представлены моими учениками. Каждый из них отстаивал целесообразность своего способа. Один из них предложил ввести единичный отрезок для наглядного решения задачи. Но потом этот ученик понял, что в этой задаче это сделать легко, потому, что скорости и расстояния кратны 5. А вот в пункте б) уже привязка к конкретной величине единичного отрезка не приносит успеха. Учащиеся во время решения всех трех задач из этого пункта самостоятельно выбирают понятные, простые для себя способы решения. На уроке можно разобрать № 564 (а, б), а домой можно задать № 564 (в).

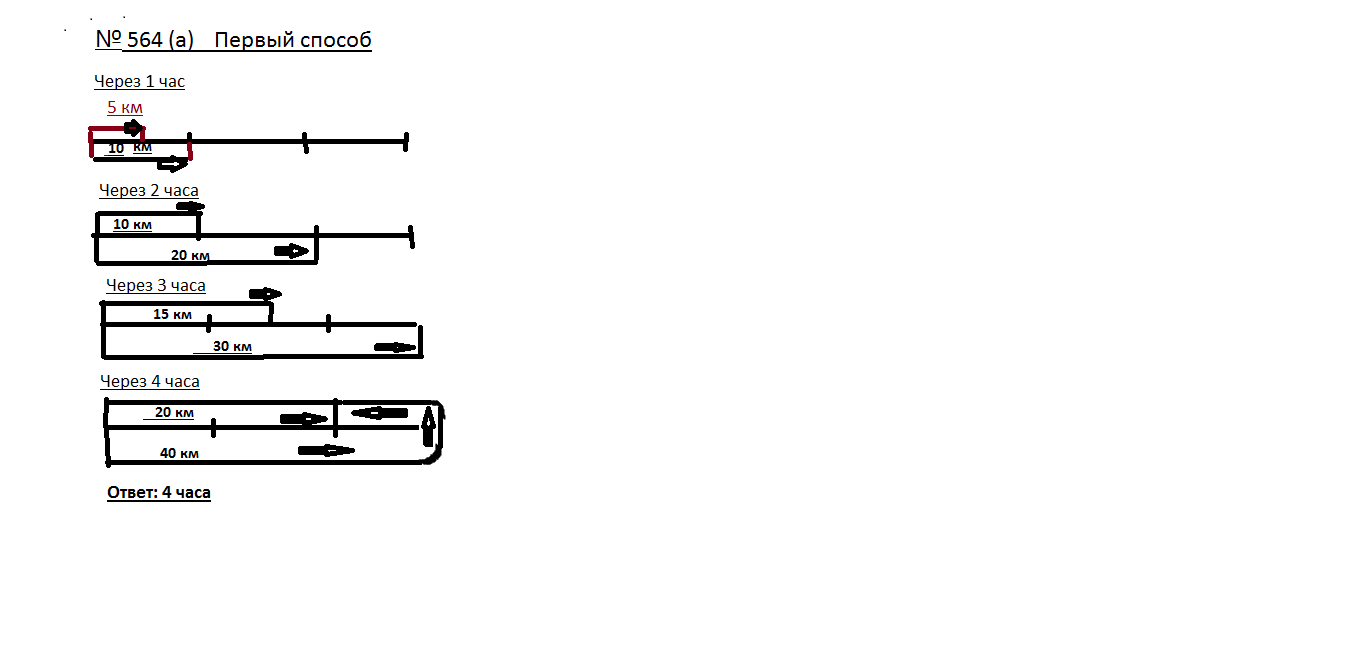
рис.13

рис.14

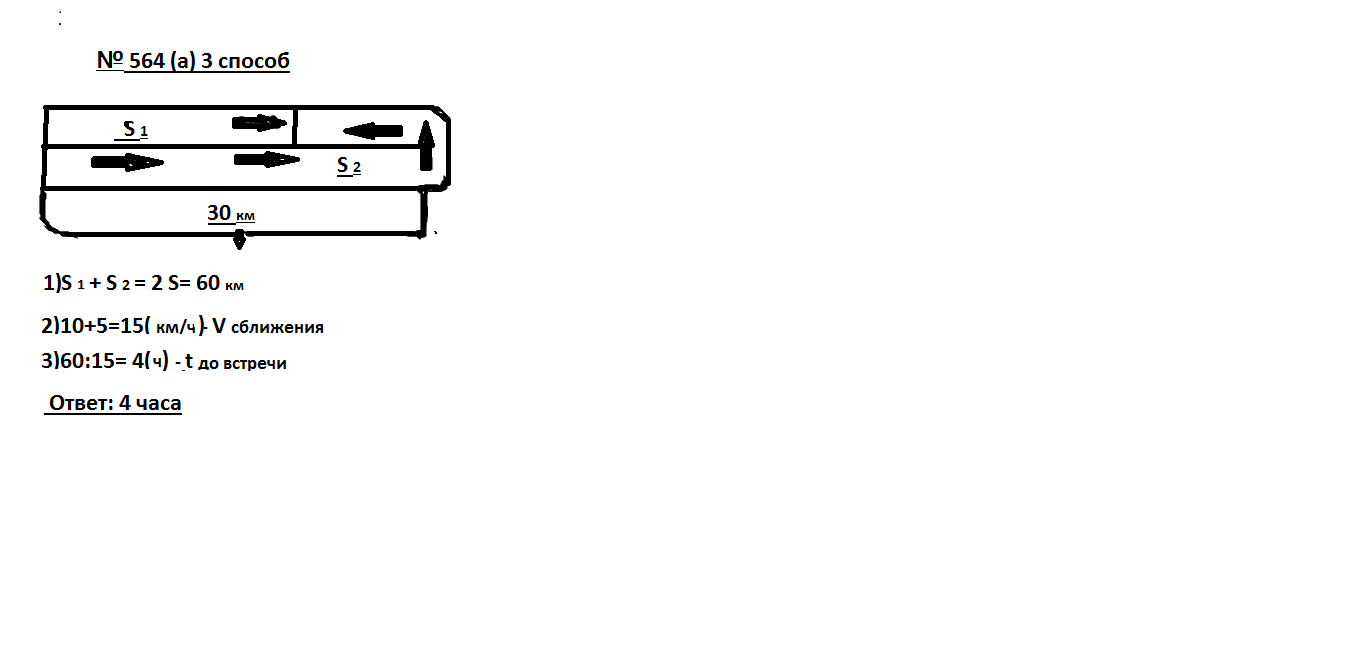
рис.14

б) Из пункта А в пункт В, расстояние между которыми 17 км, выехал велосипедист со скоростью 12 км/ч. Одновременно с ним из А в В вышел пешеход со скоростью 5 км/ч. Велосипедист доехал до В, повернул и поехал назад с той же скоростью. Через сколько часов после начала движения они встретятся?

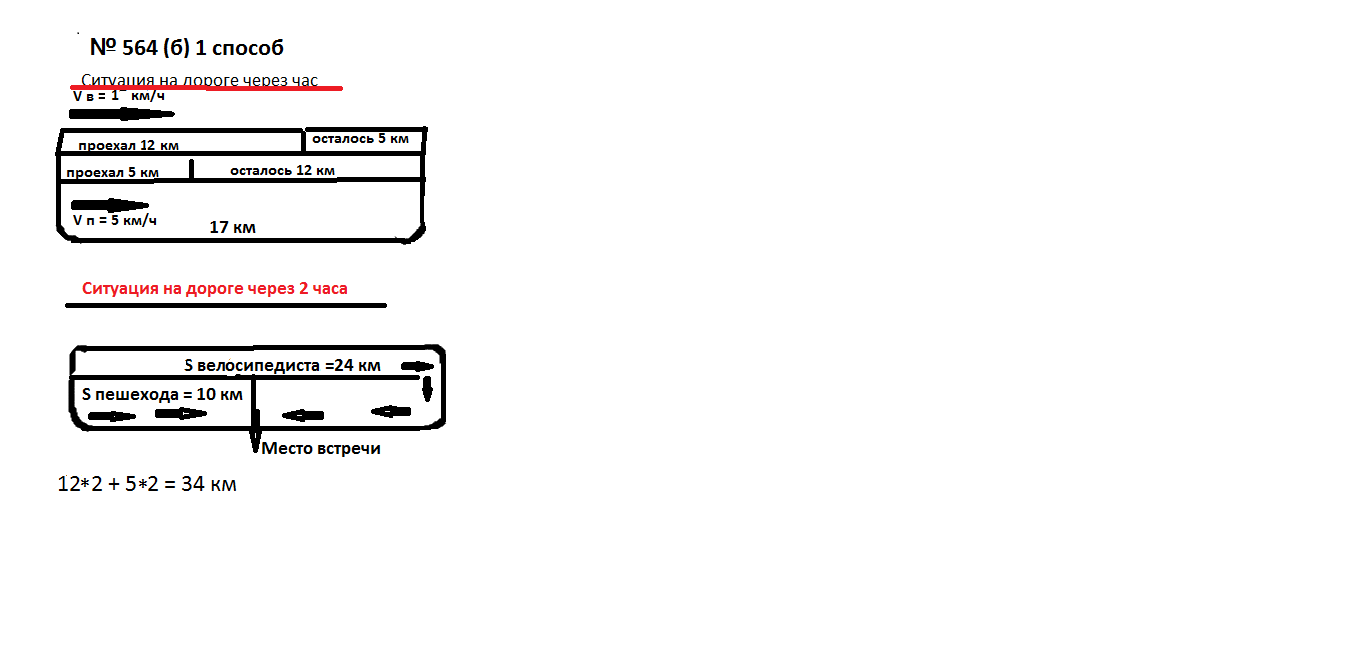
рис.15

рис.15

в) Расстояние между двумя пунктами 12 км. Из них одновременно навстречу друг другу выехали два велосипедиста со скоростью 10 км/ч и 8 км/ч. Каждый их них доехал до другого пункта, повернул и поехал назад с той же скоростью. Через сколько часов после начала движения они встретятся во второй раз?

рис.16

рис.17

Приложение 4.

Задача № 1 (Н.Я. Виленкин, 6 класс, № 1333) Смешали индийский и грузинский чай. Индийский чай составил 30% смеси. Если в эту смесь добавить еще 120 г индийского чая, то он будет составлять 45% смеси. Сколько граммов индийского чая было в смеси первоначально?

рис.18

рис.19

Задача № 2.

Две бригады, работая вместе, могут выполнить задание за 12 часов. После 8 дней совместной работы первая бригада получила другое задание, оставшуюся работа вторая бригада выполнила за 7 дней. За сколько дней выполнила бы всю работу каждая бригада?

рис.20

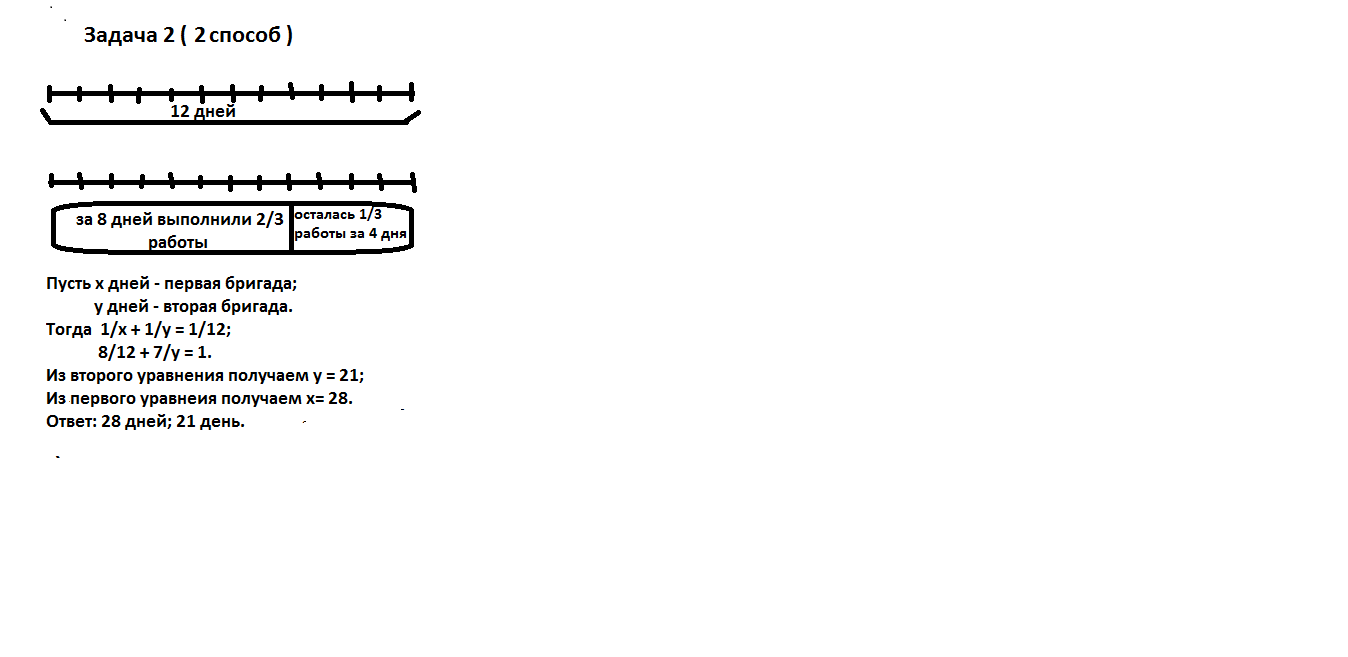
рис.21

Задача № 3.

Мотоциклист, движущийся по шоссе со скоростью 60 км/ч миновал пост ДПС. Через час мимо этого поста проехал автомобиль со скоростью 90 км/ч. На каком расстоянии от поста ДПС автомобиль догнал мотоцикл?

рис.22

рис.23