Параллельные прямые в пространстве
Введем понятие параллельных прямых в пространстве.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Параллельность прямых a и b обозначается так: 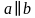 .
.
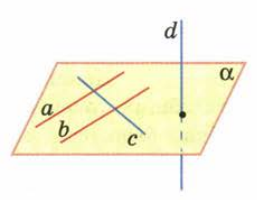
На рисунке a и b параллельны,
а прямые a и c, a и d не параллельны.
 Докажем теорему о параллельности прямых.
Докажем теорему о параллельности прямых.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
Доказательство.
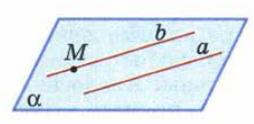
Рассмотрим прямую а и точку M, не лежащую на этой прямой.
Через прямую а и точку М проходит плоскость, и притом только одна (Следствие 1).
Обозначим эту плоскость буквой 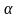 .
.
Прямая, проходящая через точку 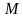 параллельно прямой
параллельно прямой 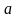 , должна лежать в одной плоскости с точкой
, должна лежать в одной плоскости с точкой 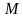 и прямой
и прямой 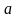 , т.е. должна лежать в плоскости
, т.е. должна лежать в плоскости 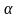 . Но в плоскости
. Но в плоскости 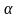 , как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна.
, как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна.
На рисунке эта прямая обозначена буквой b.
Итак, b – единственная прямая, проходящая через точку М параллельно прямой а.
Теорема доказана.
В дальнейшем нам понадобятся также понятия параллельных отрезков, параллельных отрезка и прямой, параллельных лучей.
Два отрезка называются параллельными, если они лежат на параллельных прямых. Аналогично определяется параллельность отрезка и прямой, а также параллельность двух лучей.
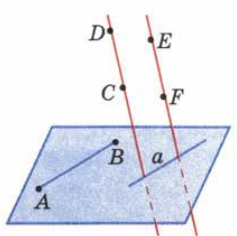
На рисунке отрезки CD и EF параллельны 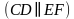 , а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а
, а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а 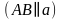 .
.
 Параллельность трех прямых
Параллельность трех прямых
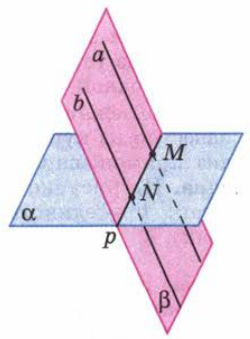
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
Из курса планиметрии известно, что если 3 прямые лежат в одной плоскости и две из них параллельны третьей прямой, то эти две прямые параллельны. Аналогичное утверждение имеет место и для трех прямых в пространстве. Сформулируем и докажем это утверждение.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство.
Пусть 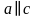 и
и 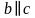 . Докажем, что
. Докажем, что 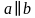 .
.
Для этого нужно доказать, что прямые а и b:
1) лежат в одной плоскости;
2) не пересекаются.
1. Отметим какую-нибудь точку К на прямой b и обозначим буквой  плоскость, проходящую через прямую а и точку К.
плоскость, проходящую через прямую а и точку К.
Докажем, что прямая b лежит в этой плоскости.
Действительно, если допустить, что прямая b пересекает плоскость 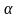 , то по лемме о пересечении плоскости параллельными прямыми прямая c также пересекает плоскость
, то по лемме о пересечении плоскости параллельными прямыми прямая c также пересекает плоскость 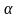 .
.
Но так как прямые а и с параллельны, то и прямая а пересекает плоскость 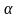 , что невозможно, ибо прямая а лежит в плоскости
, что невозможно, ибо прямая а лежит в плоскости 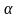 .
.
2. Прямые а и b не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые (а и b), параллельные прямой с, что невозможно.
Теорема доказана.
Методика введения темы «Параллельные прямые в пространстве»
| Деятельность учителя | Деятельность ученика |
| Введем понятие параллельных прямых в пространстве. Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются. Параллельность прямых a и b обозначается так: 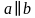 . . |
|
| Какие прямые на рисунке параллельны, а какие не параллельны? | На рисунке прямые a и b параллельны,
а прямые a и c, a и d не параллельны. |
| Докажем теорему о параллельности прямых. Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна. Что нам дано?
Что нужно доказать?
Доказательство: 1) Каким следствием из аксиомы мы воспользуемся, чтобы доказать, что существует единственная плоскость, которая проходит через прямую и точку, не лежащую на прямой? Запишем: 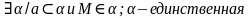 (по (по  ) )
2) Прямая, проходящая через точку 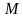 параллельно прямой параллельно прямой 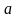 , должна лежать в одной плоскости с точкой , должна лежать в одной плоскости с точкой 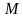 и прямой и прямой 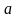 , т.е. должна лежать в плоскости , т.е. должна лежать в плоскости 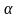 . . Запишем: 

Что из этого следует? 3) Но в плоскости 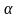 , как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b. , как известно из курса планиметрии, через точку М проходит прямая, параллельная прямой а, и притом только одна. На рисунке эта прямая обозначена буквой b. . Итак, b – единственная прямая, проходящая через точку М параллельно прямой а.
Теорема доказана. |
Дано: a – прямая
 
Доказать: 1)  2) b – единственная Доказательство: 1) Аксиома 1: через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Следовательно  . .
|
| В дальнейшем нам понадобятся также понятия параллельных отрезков, параллельных отрезка и прямой, параллельных лучей.
Какие два отрезка называются параллельными? Аналогично определяется параллельность отрезка и прямой, а также параллельность двух лучей. |
Два отрезка называются параллельными, если они лежат на параллельных прямых. |
| Какие отрезки на рисунке параллельны, а какие не параллельны? | На рисунке отрезки CD и EF параллельны 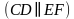 , а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а , а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а 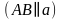 . . |
| Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость. |
|
| Из курса планиметрии известно, что если 3 прямые лежат в одной плоскости и две из них параллельны третьей прямой, то эти две прямые параллельны. Аналогичное утверждение имеет место и для трех прямых в пространстве. Попробуйте сформулировать это утверждение. |
Теорема. Если две прямые параллельны третьей прямой, то они параллельны. |
| Что нам дано?
Что требуется доказать? | Дано: 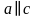
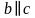
Доказать: 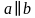
|
| Доказательство: 1) Докажем, что прямые a и b лежат в одной плоскости. Отметим какую-нибудь точку К на прямой b и обозначим буквой 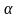 плоскость, проходящую через прямую а и точку К. плоскость, проходящую через прямую а и точку К. 

2) Пусть прямая b пересекает плоскость 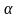 . Значит, по лемме о пересечении плоскости параллельными прямыми, прямая c также пересекает плоскость . Значит, по лемме о пересечении плоскости параллельными прямыми, прямая c также пересекает плоскость 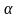 . .
Запишем: Пусть  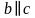 Что следует из этих утверждений? 3) Но так как прямые а и с параллельны, то и прямая а пересекает плоскость 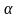 , что невозможно, ибо прямая а лежит в плоскости , что невозможно, ибо прямая а лежит в плоскости 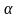 . . Запишем: 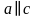

Следовательно? Получаем противоречие, т.к.  . . 4) Докажем теперь, что прямые а и b не пересекаются. Предположим, что они пересекаются. Запишем:  . .
Из этого следует, что через точку их пересечения проходят две прямые (а и b), параллельные прямой с: 
Получаем противоречие. Теорема доказана. |
Следовательно  (по лемме) (по лемме)
Следовательно  (по лемме). (по лемме). |
| Упражнение 1.
Какие две прямые на плоскости называются параллельными? Какие две прямые в пространстве называются параллельными? |
|
| Упражнение 2.
Что означают слова: «Прямые лежат в одной плоскости»? |
|
| Упражнение 3.
Покажите рукой в аудитории прямые, через которые нельзя провести плоскость. |
|
| Упражнение 4. Сколько плоскостей можно провести через две параллельные прямые? |
|
| Упражнение 5.
Прямая 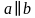 . Верно ли, что . Верно ли, что  ? ? |
|
| Упражнение 6. В параллелепипеде A… перечислите все пары параллельных ребер. перечислите все пары параллельных ребер. |
|
| Упражнение 7. Даны две параллельные прямые. Будут ли все прямые, пересекающие обе данные прямые, лежать в одной плоскости? Почему? |
|
| Упражнение 8. Верно ли для пространства утверждение, справедливое на плоскости:
«Две прямые, перпендикулярные двум параллельным прямым, параллельны»? |
|
| Упражнение 9. Сколько пар параллельных ребер имеет: а) тетраэдр; б) треугольная призма; в) октаэдр? |
|
| Упражнение 10. Даны две параллельные прямые и точка, не принадлежащая им. Установите, принадлежит ли точка плоскости этих прямых. |
|





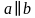 .
. Докажем теорему о параллельности прямых.
Докажем теорему о параллельности прямых.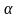 .
.
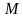 параллельно прямой
параллельно прямой 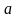 , должна лежать в одной плоскости с точкой
, должна лежать в одной плоскости с точкой 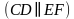 , а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а
, а отрезки AB и CD не параллельны, отрезок AB параллелен прямой а 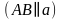 .
. Параллельность трех прямых
Параллельность трех прямых
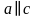 и
и 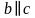 . Докажем, что
. Докажем, что 
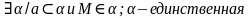 (по
(по 









