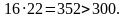Методы решения линейных уравнений в целых числах
1. Метод прямого перебора
Пример 1. В клетке сидят кролики и фазаны. Всего у них 18 ног. Узнать, сколько в клетке тех и других. Указать все решения.
Решение. Пусть х – количество кроликов, у – количество фазанов, тогда имеем уравнение:
4х + 2у = 18
2х + у = 9
у = 9 – 2х
Если х = 1, то у = 9 – 2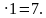
Если х = 2, то у = 9 – 2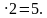
Если х = 3, то у = 9 – 2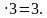
Если х = 4, то у = 9 – 2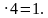
Если х = 5, то у = 9 – 2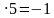 – не удовлетворяет условию задачи.
– не удовлетворяет условию задачи.
Ответ: 1 кролик и 7 фазанов или 2 кролика и 5 фазанов или 3 кролика и 3 фазана или 4 кролика и 1 фазан.
2. Использование неравенств
Пример 2. Решить в натуральных числах уравнение 5х + 8у = 39.
Решение. Для уменьшения перебора вариантов рассмотрим неравенства
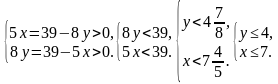
Проведем перебор по неизвестной у с учётом условия 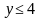 . Предварительно выразим х:
. Предварительно выразим х:
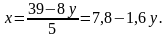
Если у = 1, то 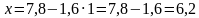 не является натуральным числом.
не является натуральным числом.
Если у = 2, то 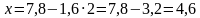 не является натуральным числом.
не является натуральным числом.
Если у = 3, то 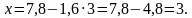
Если у = 4, то 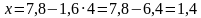 не является натуральным числом.
не является натуральным числом.
Ответ: (3; 3).
3. Использование отношения делимости
Пример 3. Имеются контейнеры двух видов: по 130 кг и 160 кг. Сколько было контейнеров первого и сколько второго вида, если вместе они весят 3 тонны? Указать все решения.
Решение. Пусть х – количество контейнеров первого вида, у – количество контейнеров второго вида, тогда имеем уравнение:
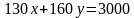
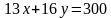
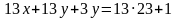
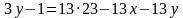
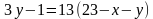
Значит, разность 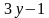 делится на 13.
делится на 13.
Если 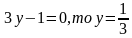 не является натуральным числом.
не является натуральным числом.
Если 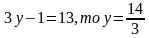 не является натуральным числом.
не является натуральным числом.
Если 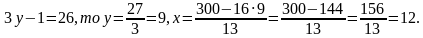
Если 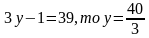 не является натуральным числом.
не является натуральным числом.
Если 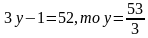 не является натуральным числом.
не является натуральным числом.
Если 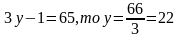 , но
, но 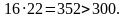
Ответ: 12 контейнеров по 130 кг и 9 контейнеров по 160 кг.
4. Выделение целой части
Пример 4. У осьминога 8 ног, а у морской звезды 5. Сколько в аквариуме тех и других, если всего у них 39 ног?
Решение. Пусть х – количество осьминогов, у – количество морских звёзд, тогда получаем уравнение:
8х + 5у = 39.
Выразим у из уравнения и выделим целую часть:
Значит, разность  делится на 5.
делится на 5.
Если не является натуральным числом.
Если
Если не является натуральным числом.
Если не является натуральным числом.
Если
Ответ: 3 осьминога и 3 морские звезды.
Замечание. В двух последних примерах использовано отношение делимости, при этом уравнения приводились к разному виду.
Пример 5. Группу школьников нужно перевезти из летнего лагеря одним из двух способов: либо двумя автобусами типа А за несколько рейсов, либо тремя автобусами типа В за несколько рейсов, причём в этом случае число рейсов каждого автобуса типа В будет на один меньше, чем рейсов каждого автобуса типа А. В каждом из случаев автобусы заполняются полностью. Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа В входит на 7 человек меньше, чем в автобус типа А.
Решение. Пусть в автобус типа В входит х человек, а в автобус типа А входит х + 7 человек, и пусть каждый их трёх автобусов типа В сделает по у рейсов, а каждый из двух автобусов типа А по у + 1 рейсов. Так как в обоих случаях автобусы перевезут одно и то же количество детей, получаем уравнение:




При  получаем:
получаем:
Число  – это один из восьми делителей числа 42.
– это один из восьми делителей числа 42.
Если
Если
Если
Если
Если
Если
Если
Если
Значит, все возможные решения: (15; 44), (16; 23), (17; 16), (20; 9), (21; 8), (28; 5), (35; 4), (56; 3).
Для каждой пары найдем количество перевозимых детей:
Из них выбираем наибольшее – это число 1980.
Ответ: 1980 детей перевозятся тремя автобусами типа В (по 15 человек) за 44 рейса или двумя автобусами типа А (по 22 человека) за 45 рейсов.
5. Метод остатков
Пример 6. Решить в целых числах уравнение 3х  4у = 1.
4у = 1.
Решение. Перепишем уравнение в виде 3х  4у + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая.
4у + 1. Поскольку левая часть уравнения делится на 3, то должна делиться на 3 и правая часть. Рассмотрим три случая.
1. Если не делится на 3.
2. Если не делится на 3.
3. Если делится на 3, поэтому 3х
Ответ: 
6. Метод спуска
Пример 7. Решить в целых числах уравнение 5х  7у = 3.
7у = 3.
Решение. Выразим из уравнения то неизвестное, коэффициент при котором меньше по модулю:
Дробь  должна быть равна целому числу. Положим целое число. Тогда
должна быть равна целому числу. Положим целое число. Тогда  Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования:
Из последнего уравнения выразим то неизвестное, коэффициент при котором меньше по модулю, и проделаем аналогичные преобразования:
Дробь  должна быть целым числом. Обозначим целое число. Отсюда
должна быть целым числом. Обозначим целое число. Отсюда  Последовательно возвращаемся к неизвестным х и у:
Последовательно возвращаемся к неизвестным х и у:
Ответ: 
7. Метод последовательного уменьшения коэффициентов по модулю
Пример 8. Решить в целых числах уравнение 79у  23х = 1.
23х = 1.
Решение. Проведём деление с остатком 79 =  и перепишем исходное уравнение в виде:
и перепишем исходное уравнение в виде:
Левая часть последнего уравнения делится нацело на 23, поэтому и правая часть должна делиться на 23. Имеем .
Для полученного нового уравнения повторим процедуру уменьшения коэффициентов:

Проведём ещё раз процедуру уменьшения коэффициентов:


Выразим  и
и  через
через  . Так как
. Так как  , то
, то
Ответ: 
 где
где 
Замечание. В последних двух примерах применён метод последовательного уменьшения коэффициентов по модулю, при этом уравнения приводились к разному виду.
8. Использование формул
Теорема 1. Уравнение  разрешимо в целых числах тогда и только тогда, когда
разрешимо в целых числах тогда и только тогда, когда
Теорема 2. Пусть уравнение  разрешимо Z и пара (
разрешимо Z и пара ( является частным решением этого уравнения. Тогда множеством всех решений в Z данного уравнения является множество пар (х; у), где
является частным решением этого уравнения. Тогда множеством всех решений в Z данного уравнения является множество пар (х; у), где
Следствие. Пусть  взаимно просты и (
взаимно просты и ( какое-нибудь решение уравнения
какое-нибудь решение уравнения
 (1)
(1)
Тогда формулы 
 при
при  дают все решения уравнения (1).
дают все решения уравнения (1).
Пример 9. Остаток от деления некоторого натурального числа  на 6 равен 4, остаток от деления
на 6 равен 4, остаток от деления  на 15 равен 7. Чему равен остаток от деления
на 15 равен 7. Чему равен остаток от деления  на 30?
на 30?
Решение. Из условия задачи следует, что существует натуральное число  такое, что
такое, что  Аналогично имеем Исключая из этих двух равенств
Аналогично имеем Исключая из этих двух равенств  , получим уравнение:
, получим уравнение:



Для решения этого уравнения найдём какое-нибудь частное решение в целых (не обязательно неотрицательных) числах. Подбором в качестве такого частного решения можно взять, например, 
 Согласно следствию уравнение
Согласно следствию уравнение  имеет решения
имеет решения 
 где
где  . Чтобы числа
. Чтобы числа  и
и  были неотрицательными, параметр
были неотрицательными, параметр  должен принимать натуральные значения. Теперь имеем
должен принимать натуральные значения. Теперь имеем
Ответ: 22.
Пример 10. Решить в целых числах уравнение 147х  25у = 14.
25у = 14.
Решение. Числа 147 и  25 взаимно просты, следовательно, уравнение разрешимо в
25 взаимно просты, следовательно, уравнение разрешимо в  . Найдём одно частное решение:
. Найдём одно частное решение:
147 = (



1 = 19 – 3
Итак, 1 = 147  . Следовательно,
. Следовательно,
14 = 147 
Значит, пара чисел (112; 658) образует частное решение данного уравнения.
Следовательно, общее решение
Ответ: 

9. Использование конечных цепных дробей
Цепная дробь (или непрерывная дробь) – это математическое выражение вида
где  есть целое число и все остальные
есть целое число и все остальные  натуральные числа. Любое действительное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Для рациональных чисел может быть использован алгоритм Евклида для быстрого получения разложения в цепную дробь.
натуральные числа. Любое действительное число можно представить в виде цепной дроби (конечной или бесконечной). Число представляется конечной цепной дробью тогда и только тогда, когда оно рационально. Для рациональных чисел может быть использован алгоритм Евклида для быстрого получения разложения в цепную дробь.
Пример 11. Решить в целых числах уравнение 127х  52у + 1 = 0.
52у + 1 = 0.
Решение. Преобразуем отношение коэффициентов при неизвестных. Прежде всего выделим целую часть неправильной дроби 

Правильную дробь  заменим равной ей дробью
заменим равной ей дробью  Тогда получим
Тогда получим
 .
.
Проделаем такие же преобразования с полученной в знаменателе неправильной дробью 
Теперь исходная дробь примет вид
Повторяя те же рассуждения для дроби  , получим
, получим
Выделяя целую часть неправильной дроби  придём к окончательному результату:
придём к окончательному результату:
Отбросив последнее звено этой цепной дроби – одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем её из исходной дроби 
Приведём полученное выражение к общему знаменателю и отбросим его, тогда

Из сопоставления этого равенства с уравнением 127х  52у + 1 = 0 следует, что х = 9, у = 22 будет решением этого уравнения, и согласно теореме все его решения будут содержаться в формулах х = 9 + 52t, у = 22 + 127t,
52у + 1 = 0 следует, что х = 9, у = 22 будет решением этого уравнения, и согласно теореме все его решения будут содержаться в формулах х = 9 + 52t, у = 22 + 127t, 
Ответ: х = 9 + 52t, у = 22 + 127t, 







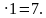
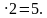
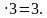
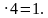
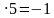 – не удовлетворяет условию задачи.
– не удовлетворяет условию задачи.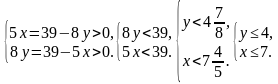
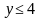 . Предварительно выразим х:
. Предварительно выразим х: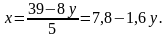
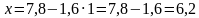 не является натуральным числом.
не является натуральным числом.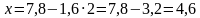 не является натуральным числом.
не является натуральным числом.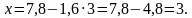
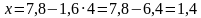 не является натуральным числом.
не является натуральным числом.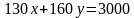
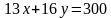
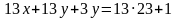
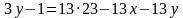
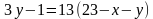
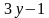 делится на 13.
делится на 13.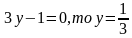 не является натуральным числом.
не является натуральным числом.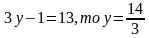 не является натуральным числом.
не является натуральным числом.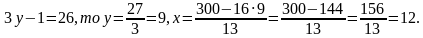
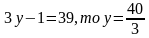 не является натуральным числом.
не является натуральным числом.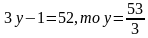 не является натуральным числом.
не является натуральным числом.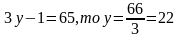 , но
, но