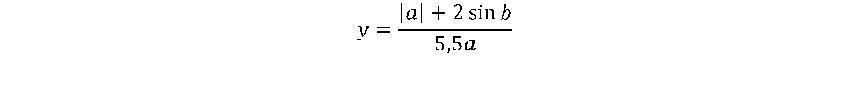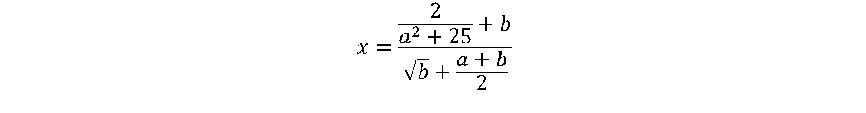Задачи на использование математических функций
Операцию возведения в степень не использовать
Известна сторона квадрата. Подготовить лист для расчета его площади.
|
| A | B | C |
| 1 | Задайте сторону квадрата |
|
|
| 2 | Площадь квадрата равна: |
|
|
| 3 |
|
|
|
| 4 |
|
|
|
Известна площадь квадрата. Оформить лист для расчета его стороны.
Известна площадь круга. Оформить лист для определения его диаметра.
Даны катеты прямоугольного треугольника. Подготовить лист для расчета его гипотенузы. Решение оформить в виде:
|
| A | B | C |
| 1 |
|
|
|
| 2 | Задайте первый катет |
|
|
| 3 | Задайте второй катет |
|
|
| 4 | Гипотенуза равна: |
|
|
Даны стороны прямоугольника. Оформить лист для расчета его диагонали.
Известна длина стороны равностороннего треугольника. Оформить лист для определения его высоты.
Оформить лист для расчета среднего геометрического двух заданных целых чисел.
Даны стороны прямоугольного параллелепипеда. Оформить лист для определения его диагонали.
Считая, что Земля – идеальная сфера с радиусом R≈6350 км, определить расстояние от точки, с заданной высотой над Землей до линии горизонта.
Оформить лист для расчета периметра прямоугольного треугольника по известным катетам.
Известна площадь квадрата. Оформить лист для расчета его диагонали.
Даны стороны треугольника. Оформить лист для определения его площади.
Известны координаты двух точек на плоскости. Оформить лист для вычисления расстояния между ними.
Даны основания и высота равнобедренной трапеции. Подготовить лист для вычисления ее периметра.
Треугольник задан координатами своих вершин. Подготовить лист для вычисления его периметра и площади.
Подготовить лист для расчета синуса, косинуса, тангенса и котангенса угла, значение которого будет вводиться в одну из ячеек. Рассмотреть 2 варианта:
значение угла указывается в радианах;
значение угла указывается в градусах.
Подготовить лист для определения абсолютной величины числа, значение которого будет вводиться в одну из ячеек.
Известна диагональ квадрата. Оформить лист для расчета его площади и периметра.
Подготовить лист для определения площади ромба по известной длине его стороны и значению внутреннего угла в градусах.
Даны стороны параллелограмма и значение одного из внутренних углов (в градусах). Подготовить лист для определения площади параллелограмма.
Даны стороны треугольника и угол между ними (в градусах). Подготовить лист для определения площади треугольника.
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для определения периметра треугольника. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
Известны размеры большего основания и боковой стороны равнобедренной трапеции, а также угол при большем основании. Подготовить лист для определения периметра трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
Дано основание равнобедренного треугольника, а также угол при основании. Подготовить лист для вычисления площади треугольника.
Подготовить лист для определения угла по известному значению его:
Синуса;
Косинуса;
Тангенса;
Котангенса.
Во всех случаях определить величину угла в радианах и градусах.
Известны длины сторон равнобедренного треугольника. Подготовить лист для вычисления его внутренних углов (в градусах).
Известны размеры оснований и боковой стороны равнобедренной трапеции. Подготовить лист для вычисления угла (в градусах) при большем основании.
Даны стороны a, b, c треугольника. Подготовить лист для вычисления его углов (в градусах) по теореме косинусов:
A=arcos(b2 + c2 – a2)/2bc
Даны катеты прямоугольного треугольника. Подготовить лист для вычисления острых углов треугольника (в градусах).
Даны основание и высота равнобедренного треугольника. Подготовить лист для вычисления угла (в градусах) при основании.
Известны размеры диагоналей ромба. Подготовить лист для вычисления его внутренних углов (в градусах).
Даны координаты на плоскости двух точек. Подготовить лист для вычисления угла наклона к оси абсцисс прямой, соединяющей эти точки.
Подготовить лист для нахождения десятичного логарифма числа, которое будет указываться в одной из ячеек.
Подготовить лист для нахождения натурального логарифма числа, которое будет указываться водной из ячеек.
Подготовить лист для вычисления значений eπ и πe.
Дана гипотенуза прямоугольного треугольника, а также один из его острых углов (в градусах). Подготовить лист для вычисления катетов этого треугольника.
Известна длина диагонали прямоугольника, а также угол ее наклона к большей стороне прямоугольника. Оформить лист для расчета площади и периметра прямоугольника.
Известны размеры большего основания и боковой поверхности равнобедренной трапеции, а также угол при большем основании. Подготовить лист для вычисления периметра и площади трапеции. Функции КОРЕНЬ и СТЕПЕНЬ и операцию возведения в степень не использовать.
Оформить лист для расчета значения функций
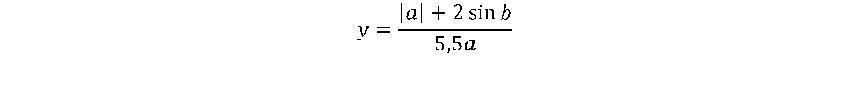
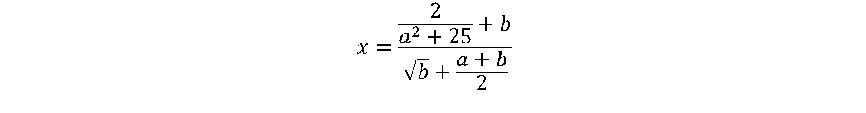
при данных значениях a и b
Считая, что Земля – идеальная сфера с радиусом R ≈ 6350 км, подготовить лист для определения расстояния до линии горизонта от точки с высотой над Землей, равной 1, 2, …, 10 км.
Получить на листе 10 первых чисел Евклида. Числа Евклида вычисляются по формуле:
Ek = 2k-1(2k-1), k = 1, 2, 3, …
Получить на листе 8 первых чисел ферма. Числа Ферма вычисляются следующим образом:
Fk = 2A+1, A = 2k+1, k = 1, 2, 3, …
Подготовить на листе таблицу значений функции y = sin(x), где х меняется от 0 до 6,5 радиан с шагом 0,5.
Получить на листе таблицу значений sin2, sin3, …, sin20 (значения углов указаны в радианах.
Получить на листе таблицу значений tg5, tg6, …, tg15 (значения углов указаны в радианах).
Получить на листе таблицу значений тригонометрических функций y = sin(x/2),
y = sin(2x), y = cosx для x, равного 00, 200, 400, …, 7200.
Пусть функция y(x) задана таблицей:
| x | y |
| x1 | y1 |
| x2 | y2 |
| … | … |
| xn | yn |
Значения аргумента х расположены в порядке возрастания, но не обязательно равномерно. Предположим, что точки (хi, уi) последовательно соединены отрезками прямых линий. Угловым коэффициентом каждого отрезка называется дробь:
(yi-1 - yi)/ (xi-1 - xi)
Оформить лист, на котором для каждого отрезка определить:
Около стены наклонно стоит палка длиной 4,5 м. Один ее конец находится на расстоянии 3 м от стены. Нижний коней палки начинает скользить в плоскости, перпендикулярной стене. Оформить на листе таблицу для определения значения угла между палкой и полом (в градусах) с момента начала скольжения до падения палки через каждые 0,2 м.
Плотность воздуха убывает с высотой по закону p=p0e-bz, где p – плотность на высоте b метров, p0 =1,29 кг/м3, z=1,25*10-4. Получить на листе таблицу зависимости плотности от высоты для значений от 0 до 1000 м через каждые 100 м.
Получить на листе значения sin1, sin1+sin2, sin1+ sin2+sin3, …, sin1+sin2+…+ sin10. Значения получить в ячейках B2:B11, введя формулу только в одну ячейку и распространив (скопировав) ее на остальные ячейки диапазона.
|
| A | B | C |
| 1 |
|
|
|
| 2 | 1 | 0,841471 |
|
| 3 | 2 | 1,750768 |
|
| 4 | 3 | 1,891888 |
|
| 5 | 4 | 1,135086 |
|
| 6 | 5 | 0,176162 |
|
| 7 | 6 | -0,10325 |
|
| 8 | 7 | 0,553733 |
|
| 9 | 8 | 1,543091 |
|
| 10 | 9 | 1,955209 |
|
| 11 | 10 | 1,411188 |
|
| 12 |
|
|
|
Получить на листе значения 1/ sin1, 1/( sin1+sin2), …, 1/(sin1+sin2+…+ sin10).
Значения получить С2:С11, введя формулу только в ячейки В2 и С2 и распространив (скопировав) их на остальные ячейки диапазона В2:С11.
|
| A | B | C | D |
| 1 |
|
|
|
|
| 2 | 1 |
| 1,188395 |
|
| 3 | 2 |
| 0,571178 |
|
| 4 | 3 |
| 0,528572 |
|
| 5 | 4 |
| 0,880991 |
|
| 6 | 5 |
| 5,676604 |
|
| 7 | 6 |
| -9,68487 |
|
| 8 | 7 |
| 1,805925 |
|
| 9 | 8 |
| 0,64805 |
|
| 10 | 9 |
| 0,511454 |
|
| 11 | 10 |
| 0,708623 |
|
| 12 |
|
|
|
|
Получить на листе значения cos1/sin1, (cos1+ cos2, )/ (sin1+sin2), …,( cos1+…+ cos15)/( sin1+…+ sin15).
Значения получить в ячейках F2:F11, введя формулы только в ячейки второй строки и распространив (скопировав) их на остальные ячейки диапазона В2: F11.
|
| A | B | C | D | E | F | G |
| 1 |
|
|
|
|
|
|
|
| 2 | 1 |
|
|
|
| 0,642093 |
|
| 3 | 2 |
|
|
|
| 0,070915 |
|
| 4 | 3 |
|
|
|
| -0,45766 |
|
| 5 | 4 |
|
|
|
| -1,33865 |
|
| 6 | 5 |
|
|
|
| -7,01525 |
|
| 7 | 6 |
|
|
|
| 2,669616 |
|
| 8 | 7 |
|
|
|
| 0,863691 |
|
| 9 | 8 |
|
|
|
| 0,215641 |
|
| 10 | 9 |
|
|
|
| -0,29581 |
|
| 11 | 10 |
|
|
|
| -1,00444 |
|
| 12 |
|
|
|
|
|
|
|
Литература:
Д.М. Златопольский. Задачник по Excel, 2002, №24. Информатика