Конспект урока по алгебре в 8-м классе "Метод интервалов"
Цели:
- совершенствовать умения решать квадратные неравенства методом интервалов, записывать решение в виде числового промежутка,
- коррекция и контроль знаний по теме «Квадратные неравенства»,
- развивать логическое мышление, навыки самостоятельной работы, умение обосновывать ход действий,
- воспитывать внимание, сознательное отношение к учению.
Задачи:
Образовательные:
знать и уметь применять название числовых промежутков и их обозначение;
алгоритм решения неравенств методом интервалов;
проконтролировать уровень усвоения способов решения квадратных неравенств;
продолжить работу по отработке умений применять алгоритмы решения квадратных неравенств;
продолжить формирование навыков само- и взаимоконтроля;
Развивающие:
проверить уровень самостоятельности мышления по применению алгоритмов;
продолжить формирование умений сравнивать алгоритмы;
создавать условия для повышения у учащихся интереса к изучению математики.
Воспитательные:
содействовать воспитанию у учащихся:
трудолюбия и усидчивости;
сознательной дисциплины на уроке.
Конспект урока
1. Организационный момент
Дидактическая цель: стимулирование деятельности учащихся, обеспечение их общей готовности.
Функция: организующая.
Задача этапа: обеспечение своевременного и организованного начала урока.
Проверка отсутствующих, проверка рабочих мест, обеспечение эмоционального настроя учащихся.
Здравствуйте ребята. Садитесь. Наш урок мне хочется начать со слов В.М. Ломоносова “Математику уже затем учить следует, что она ум в порядок приводит”.Вот и начнем приводить ум в порядок.
Мы начали изучать параграф «Метод интервалов» в главе «Квадратные неравенства». Сегодняшний наш урок будет посвящен повторению материала темы «Квадратные неравенства» и совершенствованию умению решать квадратные неравенства методом интервалов. Цель нашего урока – проверить, как вы усвоили материал прошлого урока. Т. е. мы сегодня должны показать все чему мы научились за это время.
Наш урок сегодня не совсем обычный – это урок игра «Стадион рекордов Гиннеса».
Вы, наверное, слышали о книге рекордов Гиннеса. В этой книге фиксируются все самые выдающиеся достижения и самые курьезные случаи в разных странах. Сегодня эта книга находится в нашей школе на нашем уроке. Как вы думаете, почему? Сегодня мы будем устанавливать «рекорд по решению квадратных неравенств». Имя того, кто за урок решит больше всего квадратных неравенств, будет занесено в эту книгу. Кроме этого победитель и ученики, занявшие второе и третье места, получат дипломы.
Соревнования будут проходить в видетроеборья.
Этапы троеборья:
Толкание ядра.
Бег.
Прыжки в высоту.
И как в любых соревнованиях перед их началом будет проведена разминка.
С правилами каждого этапа соревнований вы будете ознакомлены непосредственно перед его началом. По окончании каждого этапа будут подводиться его итоги. Результаты вы будете фиксировать в листах контроля, которые у каждого лежат на столе. Там же будете фиксировать занятое место и «улыбку настроения». Я, в свою очередь, буду все фиксировать на экране на доске.
Ну что, готовы начать работу? Тогда приступим.
2. Повторение.
Дидактическая цель: выявление и анализ имеющихся у учащихся знаний, умений и навыков.
Функция: контрольно-оценочная.
Задачи этапа:
контроль знаний и умений, полученных при изучении данной темы; выявление опорных знаний;
выявление уровня усвоения знаний.
Способы решения: совокупность вопросов, практические задания.
Формы работы: индивидуальная.
Этот этап урока будет проводиться в виде «Разминки».
«РАЗМИНКА»
«Разминка» - предварительный этап нашего математического турнира.
Разминка будет проходить в два тура:
Повторение теории по теме.
Устный счет.
Цель данного этапа: Проверить усвоение теоретического материала главы, знание определений и формул, а также умение устно выполнять несложные задания по теме квадратные уравнения и неравенства: решать линейные неравенства, проверять корни уравнений и неравенств, записывать ответы разными способами.
ТЕОРЕТИЧЕСКИЙ ТУР.
Нужно ответить на поставленные вопросы.
ВОПРОС №1. Какие неравенства называются квадратными?
Ответ: Неравенства, у которых в левой части стоит квадратный трехчлен, а в правой нуль.
ВОПРОС №2. Какими способами можно решить квадратное неравенство?
Ответ: Квадратное неравенство можно решить графическим способом и методом интервалов.
ВОПРОС №3.По какой формуле раскладываем на множители квадратный трехчлен?
Ответ:По формуле а(х – х1)(х –х2) где х1 и х2 - корни соответствующего квадратного уравнения.
ВОПРОС №4. По какой формуле находят корни квадратного уравнения?
Ответ: Корни квадратно уравнения ах2 + вх+ с = 0находятся по формуле: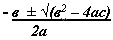
ВОПРОС №5. Как называется подкоренное выражение в2 – 4ас?
Ответ: Дискриминант.
ВОПРОС №6.Как решить квадратное неравенство графическим способом?
Ответ:Нужно определить направление ветвей параболы по знаку первого коэффициента, затем найти корни соответствующего квадратного уравнения (точки пересечения с осью Ох), построить эскиз графика и по нему определить промежутки, где функция положительна, а где отрицательна.
ВОПРОС №7. Что является графиком квадратичной функции?
Ответ: Парабола.
ВОПРОС №8. . Как решить квадратное неравенство методом интервалов?
Ответ: Нужно найти корни соответствующего квадратного уравнения. Отметить получившиеся числа накоординатной прямой, определить знак неравенства на каждом из получившихся числовых промежутков, которые называются интервалами.
ВОПРОС №9. Какие числовые промежутки вы знаете?
Ответ: Отрезки, интервалы, полуинтервалы и лучи.
ВОПРОС №10.Почему в ответе могут получиться разные числовые промежутки?
Ответ: Это происходит, потому что неравенства бывают строгие и нестрогие. Строгие, в которых знак , нестрогие - в которых знак ≤ или ≥.
Хорошо, а теперь подведем итоги этого этапа.
Оцениваться будет ваша активность - поднятая рука и полнота ответа. Во время ваших ответов я буду помечать себе, кто как отвечает. И так, ставим в ваши листы контроля, следующие оценки:
Оценка «5» соответствует первому месту,оценка «4» - второму, «3» - третьему, «2» - четвертому.
А теперь «УСТНЫЙ СЧЕТ» - второй тур нашей разминки.
Работать будем с перфокартами. У вас на карточках даны задания с выбором ответа. Вам нужно выполнить предложенное задание, найти получившийся ответ и в окошечке около него поставить крестик. (Выдают ученикам перфокарты).
ЗАДАНИЕ №1. Решите неравенство:
ЗАДАНИЕ №2. Решить систему и записать ответ в виде числового промежутка.
| - х -8 2х + 7 ≥ 0 | ( - 3,5; 8) [-3,5; 8] (-3,5; 8] [-3,5; 8) |
ЗАДАНИЕ №3. Изобразить на координатной прямой множество чисел, удовлетворяющих двойному неравенству: - 2

ЗАДАНИЕ №4 .Запишите промежуток чисел
( -5; 3] в виде двойного неравенства.
-5
-5
3
3
ЗАДАНИЕ №5. Проверить какое из чисел является решением данного квадратного неравенства.
| 2x2 – 3x – 2
| - 0,5
-2 1 -1 |
ЗАДАНИЕ №6. Разложить на множители квадратный трехчлен
| х2 + x – 2 | (x – 2)(x + 1) ( x +2)(x + 1) (x + 2)(x – 1) (x – 2)(x – 1) |
ЗАДАНИЕ №7. Запишите решение неравенства изображенное на чертеже в виде числового промежутка. 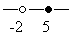
[-2; 5]
(-2; 5)
[-2; 5)
(-2; 5]
Время вышло. Подведем итоги. Снимите скрепку и выпишите буквы, около которых поставили крестики.Поднимите руку, у кого получилось слово « молодец».
Отлично. Ставим в лист контроля оценку «5» и первое место. У кого не совпала одна буква - «4» и второе место, две буквы не совпали – оценка «3», - место третье, у кого не совпали тир и меньше букв, ставят оценку два и четвертое место.
Ну вот, разминка закончилась. Переходим непосредственно к троеборью.
3.Систематизация и обобщение знаний.
Дидактическая цель: выявление главного в изученном материале.
Функция: контрольно-проверочная.
Задачи: подведение итогов работы учащихся; практическое применение знаний.
Способ решения: практикум по решению неравенств.
Форма - индивидуальная.
ТОЛКАНИЕ ЯДРА – первый этап троеборья
В этом виде спорта побеждает тот, кто дальше толкнул это ядро. У нас в роли ядра - ваши умения, а в роли метров - квадратные неравенства. Победит тот, кто больше решит квадратных неравенств.
Цель этого этапа: Проверить ваши умения в решении квадратных неравенств графическим способом. Для работы на этом этапе делимся на две группы:
Сильные ученики: …
Более слабые ученики: …
Вам даны карточки, на которых написаны квадратные неравенства. Вы должны их решить графическим способом. Ответ записываете в виде числовых промежутков. Решать неравенства можно в любом порядке, только указывать номер. Для второй группы, на столах подготовлены карточки памятки по применению алгоритмов.
Карточка №1. (для более слабых учеников)
1. (x – 3)(x +4) 0
2. (x+8)(x+2) 0
3. x2 – 3x + 2 ≤ 0
4. x2 – 2x – 3 ≥ 0
5. x2 + 2x – 3 0
Карточка №2. (для более сильных учеников)
1. 4х2 + 3x – 1
2. 5x2 – 9x +4 0
3. 25 – x2≥ 0
4. 12 2x2 + 5x
5. 3x2 + 2≥ 5x
На выполнение этого задания вам отводится 15 минут.
Время вышло. Проверим ваши успехи. Поменяйтесь тетрадями с соседями по парте.
(Ответы записаны на доске.)
Если пример решен верно, то ставим «+».Считаем плюсы. Пять плюсов – оценка «5» и первое место.Четыре плюса – оценка «4» и второе место.Три плюса – оценка «3» и третье место и т.д.
Продолжим наши соревнования.
Следующий этап троеборья – «БЕГ»
Вы знаете, что в этом виде спорта выигрывает тот, кто быстрее всех пробежит дистанцию.
У нас с вами этой дистанцией будут предложенные квадратные неравенства, одно из которых нужно решить графическим способом.
Цель этого этапа: Проверить и закрепить умение решать квадратные неравенства графическим способом.
Карточка №1. (для более слабых учащихся)
1. (x -11)(x + 8)
2. 2x2 – x 0
3. x2 – 3x – 10 0
Карточка №2. (для более сильных учащихся)
1. x2 + 2x – 15
2. 2x2 – 11x – 21 0
3. 3x(2x – 1) 2 – 10x + 2
По мере прохождения этапа учащиеся сдают тетради на проверку. Кроме скорости учитывается еще и правильность решения.
Те, кто освободился, могут взять дополнительное задание. Это будет учитываться при установлении рекорда.
Ну а теперь наступило время последнего этапа наших соревнований.
Заключительный этап наших соревнований – «ПРЫЖКИ В ВЫСОТУ»
Правила прохождения этого этапа отличаются от тех, которые существуют на настоящих соревнованиях. Если на соревнованиях на взятие высоты отводится три попытки, то у нас этих попыток не будет.
У нас победителем будет тот, кто « выше прыгнет» - решит больше всего квадратных неравенств методом интервалов.
Цель этого этапа: Проверить и закрепить умение решать квадратные неравенства методом интервалов.
Перед вами карточки с неравенствами. Решать их можно в любом порядке. На этот этап вам отводится 15 мин. Приступаем.
РЕШИТЬ НЕРАВЕНСТВО МЕТОДОМ ИНТЕРВАЛОВ (для более сильной группы)
1. (x – 1)(x + 2)
2. x2 – 3x + 2
3. 3x2 – x – 4 0
4. 2x2 – 10x + 12 ≤ 0
5. (x – 1)(x + 3)
6. (x – 4)(x – 5) ≥ 0
7. x2 – 3x – 10
8. x(x – 5)(x + 3) ≥ 0
9.2x(3x – 1) 2x2 – 13x + 3
10.4x(3x – 2) ≤ 10x2 – 6x + 1
РЕШИТЬ НЕРАВЕНСТВО МЕТОДОМ ИНТЕРВАЛОВ (для группы слабых учащихся)
1. (x + 2)(x – 7) 0
2. (x – 3)(x – 4) 0
3. (x – 5,7)(x – 7,2) 0
4. x2 + x – 12
5. 2x2 – 3x – 2 0
6. 4x2 - 4x - 3
7. x2 – 4x – 5 ≤ 0
8. x2 + 2x - 15 ≤ 0
9. 3x2 - 5x - 2 ≥ 0
10. x2 – x
(На доске зафиксированы ответы. Проверку производят сами учащиеся.)
Произведем самопроверку. Если неравенство решено верно, то ставим плюс.
А теперь подсчитаем, у кого сколько плюсов получилось.
7 – 8 плюсов ставим оценку «5»
5 – 6 плюсов ставим оценку «4»
4 – 3 плюса оценка «3»
меньше трех плюсов - оценка «2»
Ставим оценки в листы контроля. А теперь поставим места в зависимости от того, кто больше решил неравенств.Рисуем «улыбку настроения».
А теперь подведем итоги урока. Какую мы ставили цель? Выполнили мы задуманное?
Посмотрим на табло.
На сегодняшнем уроке получили оценки:
Победителем нашей игры стала ________________.
Ей мы вручаем диплом, и ее имя заносим в нашу «Книгу рекордов Гиннеса». На этом наш урок закончен. Спасибо за урок!
Ну что же, наш сегодняшний урок окончен.
СПАСИБО ЗА УРОК!
Можете быть свободны.


























