6 класс Тема 2 Отношения и пропорции
1.Что называют отношением числа a к числу b (частное двух не равных чисел a и b называют ещё отношением чисел a и b) 2.Что называют членами отношения ( числа a и b называют членами отношений)
3.Назовите свойство отношения (отношение не изменится, если его члены умножить или разделить на одно и то же число. не равное нулю)
4.Чем является отношение величин одного наименования (отношение однородных величин есть число)
5.Чем является отношение величин разных наименований (отношение величин разных наименований есть новая величина). Приведите пример
6.Что называется масштабом (отношение длины отрезка на плане к его настоящей длине)
7. Что называют пропорцией (равенство двух отношений называют пропорцией)
8.Как читают пропорцию a ∶ b = с ∶ d или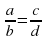 («отношение a к b равно отношению с к d» , или «a относится к b , как с относится к d»)
(«отношение a к b равно отношению с к d» , или «a относится к b , как с относится к d»)
9.Как называются члены пропорции (числа a и d называют крайними членами пропорции, а числа b и с – средними членами пропорции)
10. Назовите основное свойство пропорции (произведение крайних членов пропорции равно произведению её средних членов: если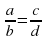 , a
, a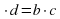 )
)
11.Как найти неизвестный крайний член пропорции (чтобы найти неизвестный крайний член пропорции надо произведение средних членов пропорции разделить на известный крайний член пропорции)
12. Как найти неизвестный средний член пропорции (чтобы найти неизвестный средний член пропорции надо произведение крайних членов пропорции разделить на известный средний член пропорции)
13.Какие величины называются прямо пропорциональными (если при увеличении одной из них в несколько раз другая увеличивается во столько же раз, или при уменьшении одной из них в несколько раз другая уменьшается во столько же раз)
14. Какие величины называются обратно пропорциональными (если при увеличении одной из них в несколько раз другая уменьшается во столько же раз, или при уменьшении одной из них в несколько раз другая увеличивается во столько же раз)
6 класс Тема 3 Проценты
1.Что называют процентом числа ( величины) -( одну сотую часть числа ( величины) называют процентом этого числа ( величины))
2.Как найти несколько процентов числа (надо 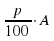 , где
, где 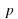 – число процентов,
– число процентов, 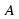 – данное число)
– данное число)
3.Как узнать, сколько процентов первое число составляет от второго числа (чтобы узнать, сколько процентов первое число составляет от второго числа, надо первое число разделить на второе и результат умножить на 100)
4.Для чего используют круговые диаграммы (для того, чтобы показать соотношение целого и его частей используют круговые диаграммы)
5.Сколько градусов содержит развёрнутый угол (развёрнутый угол содержит 180 градусов)
6 Сколько градусов содержит полный угол (развёрнутый угол содержит 360 градусов)
6 класс Тема 4 Целые числа . Сложение и вычитание целых чисел
1.Какие числа образуют целый ряд чисел (целый ряд чисел образуют натуральные числа, отрицательные числа и число нуль)
2.Какие числа называют противоположными (числа, которые отличаются только знаком, называют противоположными)
3.Какое число противоположно числу 0 ( нуль противоположное самому себе)
4. Что называют модулем положительного числа (модулем положительного числа называют само это число)
5. Что называют модулем отрицательного числа (модулем отрицательного числа называют противоположное ему число)
6.Что называют модулем числа 0 (модулем числа 0 называется число 0 )
7.Как сравнивают целые числа (из двух целых чисел больше то, которое в ряду целых чисел стоит правее)
8.Какое число больше: положительное или отрицательное ( положительное число)
9.Правило сравнения целого числа с нулём (любое положительное число больше 0, а любое отрицательное число меньше 0)
10. Правило сравнения положительного числа с отрицательным(любое положительное число больше любого отрицательного)
11. Правило сравнения отрицательного числа с отрицательным числом (из двух отрицательных чисел больше то, у которого модуль меньше)
12.Как сложить два числа с одинаковыми знаками (чтобы сложить два числа одинаковых знаков, надо сложить их модули и поставить перед суммой знак слагаемых)
13. Как сложить два числа с разными знаками (чтобы сложить два числа разных знаков и с разными модулями, надо из большего модуля вычесть меньший и перед разностью поставить знак слагаемого с большим модулем)
14.Каким числом является сумма положительных чисел (положительным числом)
15. Каким числом является сумма отрицательных чисел (отрицательным числом)
16.Чему равна сумма противоположных чисел (сумма противоположных чисел равна нуля )
17.Сформулируйте переместительный закон сложения ( от перестановки слагаемых сумма не меняется: a + b = b + a)
18. Сформулируйте сочетательный закон сложения (чтобы к сумме двух целых чисел прибавить третье целое число, можно к первому числу прибавить сумму второго и третьего: ( a +b ) + c = a + ( b+ c))
19.Что называют разностью двух целых чисел (разностью двух целых чисел называют целое число, которое в сумме с вычитаемым даёт уменьшаемое)
20.Как из одного числа вычесть другое (чтобы из одного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому: a – b = a + (-b))
6 класс Тема 5 Целые числа . Умножение и деление целых чисел
1.Что называют произведением двух не равных нулю чисел (произведением двух не равных нулю чисел называют произведение их модулей, взятое со знаком «+», если эти числа одинаковых знаков, и со знаком «-», если они разных знаков)
2.Чему равно произведение любого целого числа и нуля (равно 0 )
3.Что называют степенью числа a с натуральным показателем n (степенью числа a с натуральным показателем n (n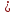 1) называют произведение n , каждый из которых равен a)
1) называют произведение n , каждый из которых равен a)
4. Чему равно частное целых чисел (частное чисел a и b равно частному их модулей, взятому со знаком «+», если эти числа одинаковых знаков, и со знаком «-», если они разных знаков)
5.Чему равно частное от деления нуля на любое целое, не равное нулю число (частное от деления нуля на любое целое, не равное нулю число a равно нулю)
6. На нуль можно делить ?( делить на 0 нельзя)
7. Распределительный закон умножения (для любых целых чисел a, b, c выполняется распределительный закон :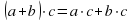 )
)
8.Что называется вынесением общего множителя за скобки? ( переход от суммы 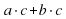 к произведению
к произведению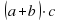 называется вынесением общего множителя за скобки)
называется вынесением общего множителя за скобки)
9.Сформулируйте правило раскрытие скобок, перед которыми стоит знак «+» (если сумма заключена в скобки, перед которыми стоит знак «+», то при раскрытии скобок знаки слагаемых оставляют без изменений)
10. Сформулируйте правило раскрытие скобок, перед которыми стоит знак «-» (если сумма заключена в скобки, перед которыми стоит знак «-», то при раскрытии скобок знаки слагаемых меняют на противоположные)
11.По какому правилу заключают в скобки сумму, если перед скобками ставят знак «+» ( если сумма заключается в скобки, перед скобками стоит знак «+», то знаки слагаемых, заключённых в скобки, оставляют без изменения)
12. По какому правилу заключают в скобки сумму, если перед скобками ставят знак «-» ( если сумма заключается в скобки, перед скобками стоит знак «-», то знаки слагаемых, заключённых в скобки, меняют на противоположные)
13. Какая прямая называется координатной осью? (прямую, на которой заданы начала отсчёта, направление отсчёта и единичный отрезок , называют координатной осью)
14. Что называют положительной координатной полуосью? (луч , идущий от нуля вправо, называют положительной координатной полуосью или положительным координатным лучом)
15. Что называют отрицательной координатной полуосью? (луч, идущий от нуля влево, называют отрицательной координатной полуосью или отрицательным координатным лучом)
16.Как называют точку, изображающую число нуль?( точку О, изображающую число нуль, называют точкой нуль или точкой с координатой нуль и пишут О(о).
17. Что называют координатой точки ( число, показывающее положение точки на координатном луче , называется координатой точки).
18. Какие точки находятся на одинаковом расстоянии от точки нуль, но на разных полуосях (точки, координаты которых противоположные числа).
6 класс Тема 6 Рациональные числа . Сложение и вычитание рациональных чисел. Умножение и деление рациональных чисел
1.Какое число называется рациональным? (число, которое можно записать в виде 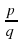 , где p и q – целые числа и q не равное нулю, называют, рациональным числом или дробью)
, где p и q – целые числа и q не равное нулю, называют, рациональным числом или дробью)
2. Является ли натуральное число рациональным?( да , является; ( дробь с числителем p и знаменателем 1 есть другая форма записи натурального числа p, 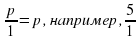 = 5,
= 5, 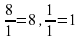 ) 3. Является ли целое число рациональным?( да , является) 4. Является ли положительная дробь рациональным числом? ( да , является)
) 3. Является ли целое число рациональным?( да , является) 4. Является ли положительная дробь рациональным числом? ( да , является)
5. Сформулируйте основное свойство дроби (если числитель и знаменатель дроби умножить на одно и то же целое число, не равное нулю, то получится равная ей дробь 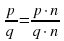 , где p,q,n – целые числа, p
, где p,q,n – целые числа, p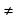 0, n
0, n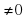 )
)
6. В каком случае дробь можно сократить?( если числитель и знаменатель дроби имеют общий множитель n – целое число, не равное нулю , то дробь можно сократить на n)
7.В каком случае дробь положительна?( дробь положительна, если p и q одного знака)
8.В каком случае дробь отрицательна? (дробь отрицательна, если p и q разных знаков)
9. Любую ли дробь можно привести к положительному знаменателю? (да)
10. Когда равны две дроби с общим знаменателем?( две дроби с общим положительным знаменателем равны, если равны их числители)
11.Как сравнить две дроби с общим знаменателем?( из двух дробей с общим знаменателем больше та, у которой числитель больше)
12. Как сравнить две дроби с разными знаменателями?(чтобы сравнить дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сравнить полученные дроби)
13.Сформулируйте правило сравнения положительной дроби с нулём(любая положительная дробь больше нуля)
14. Сформулируйте правило сравнения отрицательной дроби с нулём( любая отрицательная дробь меньше нуля)
15. Сформулируйте правило сравнения положительной дроби с отрицательной ( любая положительная дробь больше отрицательной)
16.Чему равна сумма двух дробей с общим положительным знаменателем дроби (сумма дробей с общим положительным знаменателем есть дробь с тем же знаменателем и числителем , равным сумме числителей, 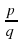 +
+  =
= 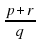 )
)
17. Как вычесть две дроби с общим положительным знаменателем?( разность двух дробей с общим положительным знаменателем есть дробь с тем же знаменателем и числителем, равный разности числителей уменьшаемого и вычитаемого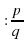 -
-  =
= 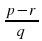 )
)
18. Чему равна сумма противоположных дробей?( сумма противоположных дробей равна нулю)
19.Как вычесть сумму или разность дробей с разными знаменателями?( чтобы вычислить сумму( или разность ) дробей с разными знаменателями, надо сначала привести их к общему положительному знаменателю 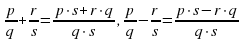 )
)
20. По какому правилу умножают дроби любого знака?(дроби любого знака умножают по тем же правилам , что и положительные дроби )
)
21. По какому правилу делят дроби любого знака? (дроби любого знака делят по тем же правилам , что и положительные дроби 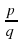 ∶
∶ =
= ) 22.Как умножить дробь на целое число?( чтобы умножить дробь на целое число, модно её числитель умножить на это число
) 22.Как умножить дробь на целое число?( чтобы умножить дробь на целое число, модно её числитель умножить на это число =
=  ) 23.Как разделить дробь на целое число, не равное нулю?( чтобы разделить дробь на целое число, не равное нулю, можно знаменатель дроби умножить на это число
) 23.Как разделить дробь на целое число, не равное нулю?( чтобы разделить дробь на целое число, не равное нулю, можно знаменатель дроби умножить на это число 
 =
= ) 24. Как разделить одну дробь на другую? (чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю
) 24. Как разделить одну дробь на другую? (чтобы одну дробь разделить на другую, отличную от нуля, можно делимое умножить на дробь, обратную делителю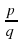 ∶
∶ =
= ) 25.Какие числа называют взаимно обратными и чему равно их произведение?(числа
) 25.Какие числа называют взаимно обратными и чему равно их произведение?(числа 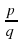 и
и  (
( ) называют взаимно обратными дробями ( числами), (произведение взаимно обратных чисел равно 1) 26. Какие законы сложения и умножения справедливы для рациональных чисел a, b,c? ( для рациональных чисел a, b,c справедливы законы арифметических действий: 1) переместительный закон сложения:
) называют взаимно обратными дробями ( числами), (произведение взаимно обратных чисел равно 1) 26. Какие законы сложения и умножения справедливы для рациональных чисел a, b,c? ( для рациональных чисел a, b,c справедливы законы арифметических действий: 1) переместительный закон сложения:
2)сочетательный закон сложения: ( 
3)переместительный закон умножения:
4)сочетательный закон умножения: ( 
5) распределительный закон умножения относительно сложения: (a + b) ∙ c = a ∙ c + b ∙ c
6) распределительный закон умножения относительно вычитания: (a - b) ∙ c = a ∙ c - b ∙ c







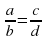 («отношение a к b равно отношению с к d» , или «a относится к b , как с относится к d»)
(«отношение a к b равно отношению с к d» , или «a относится к b , как с относится к d»)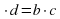 )
)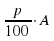 , где
, где 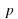 – число процентов,
– число процентов, 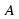 – данное число)
– данное число)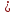 1) называют произведение n , каждый из которых равен a)
1) называют произведение n , каждый из которых равен a)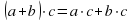 )
)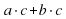 к произведению
к произведению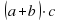 называется вынесением общего множителя за скобки)
называется вынесением общего множителя за скобки)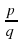 , где p и q – целые числа и q не равное нулю, называют, рациональным числом или дробью)
, где p и q – целые числа и q не равное нулю, называют, рациональным числом или дробью)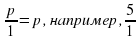 = 5,
= 5, 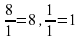 ) 3. Является ли целое число рациональным?( да , является) 4. Является ли положительная дробь рациональным числом? ( да , является)
) 3. Является ли целое число рациональным?( да , является) 4. Является ли положительная дробь рациональным числом? ( да , является)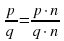 , где p,q,n – целые числа, p
, где p,q,n – целые числа, p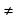 0, n
0, n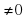 )
) =
= 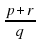 )
)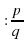 -
- 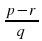 )
)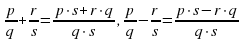 )
) )
)









