Международный конгресс математиков

Международный конгресс математиков

International Congress of Mathematicians , ICM

Выполнили:

Студентки Б-4051

Жильникова Анна

Печерская Татьяна

Афиша Первого Международного конгресса математиков

Международный математический конгресс

• Премия Филдса, с 1936 года.
• Премия Неванлинны, с 1982 года.
• Премия Гаусса, с 2006 года.
• Премия Черна, с 2010 года.
• Премия Лилавати, с 2010 года.

Предыстория

Первая встреча математиков мира

(Чикаго, 1893).

В центре нижнего ряда — Феликс Клейн.

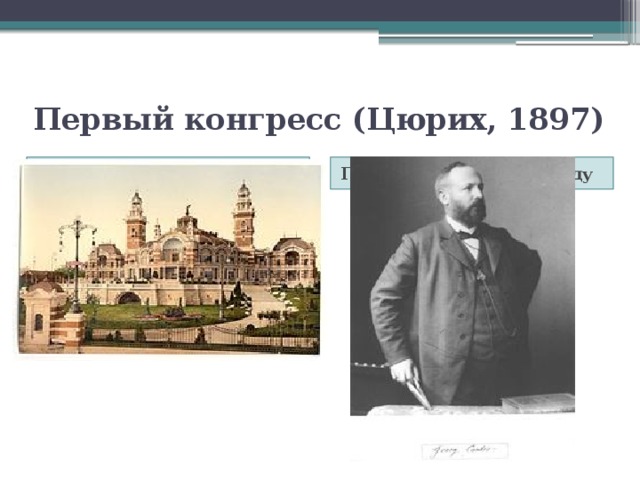
Первый конгресс (Цюрих, 1897)

Цюрихский дворец Тонхалле

Георг Кантор в 1894 году

Второй конгресс (Париж, 1900)

Давид Гильберт

Шесть секций:

• Арифметика и алгебра
• Анализ
• Геометрия
• Механика и математическая физика
• История и библиография математики
• Преподавание и методология математики

Третий конгресс (Гейдельберг, 1904)

• Пенлеве, «Современные проблемы интегрирования дифференциальных уравнений».
• Минковский, «Геометрия чисел».
• Гильберт, «Основания логики и арифметики».
• Борель, «Интерполяция непрерывных функций многочленами».
• Леви-Чивита, «Численное решение задачи трёх тел».

Четвёртый конгресс (Рим, 1908)

• Джузеппе Веронезе: «Неархимедова геометрия»
• Гёста Миттаг-Леффлер: «Арифметическое представление аналитических функций комплексной переменной»
• Саймон Ньюком: «Теория движения Луны — история и современное состояние»
• Хендрик Лоренц: «Распределение энергии между веществом и эфиром»
• Эмиль Пикар: «Математика в своих отношениях с физикой»

Пятый конгресс (Кембридж, 1912)

Панорама Кембриджского университета

Работали четыре сводные секции:

• Арифметика, анализ и алгебра.
• Геометрия.
• Прикладная математика.
• История, философия, преподавание.

VI — X Конгрессы (1920—1936)

• Шестой Конгресс (Страсбург, Франция, 1920)
• Седьмой Конгресс (Торонто, Канада, 1924)
• Восьмой Конгресс (Болонья, Италия, 1928)
• Девятый Конгресс (Цюрих, Швейцария, 1932)
• Десятый Конгресс (Осло, Норвегия, 1936)

Одиннадцатый Конгресс (Кембридж (Массачусетс), 1950)

• Президент АН СССР С. И. Вавилов направил Оргкомитету следующую телеграмму: «Академия наук СССР благодарит за получение искреннего приглашения советским ученым принять участие в работе Международного математического конгресса, проводимого в Кэмбридже. Советские математики слишком заняты своей повседневной работой и не смогут посетить конгресс. Надеюсь, что предстоящий конгресс станет важным событием для математической науки. Желаю успеха в работе конгресса.»

Двенадцатый Конгресс (Амстердам, 1954)

В рамках Конгресса состоялись также три симпозиума на актуальные темы:

• Стохастические процессы
• Алгебраическая геометрия
• Математическая интерпретация формальных систем

Тринадцатый Конгресс (Эдинбург, 1958)

Участие Советского Союза в Эдинбургском конгрессе было уже полноценным. Трое выступили с пленарными докладами:

• А. Д. Александров: «Современное развитие теории поверхностей»,
• Н. Н. Боголюбов, В. С. Владимиров: «О некоторых математических проблемах квантовой теории поля».
• Л. С. Понтрягин: «Оптимальные процессы регулирования».

Четырнадцатый Конгресс (Стокгольм, 1962)

На Конгрессе был представлен «Всемирный каталог математиков» ( World Directory of Mathematicians ).

XV Конгресс по предложению советской делегации был запланирован в Москве (1966).

Пятнадцатый Конгресс (Москва, 1966)

• Председателем Оргкомитета был ректор МГУ И. Г. Петровский.
• Московский Конгресс установил новый рекорд по числу участников: заявку подали 5600 человек, фактически приняли участие 4280. в том числе 1470 из СССР, 725 из США, 398 из обеих Германий, 286 британцев, 280 французов.
• До сих пор неизвестно, кто из французских гостей зарегистрировался как легендарный Бурбаки.

Советская почтовая марка, посвящённая XV Конгрессу (1966, Москва)

XVI — XX Конгрессы (1970—1986)

• Шестнадцатый Конгресс (Ницца, 1970)
• Семнадцатый Конгресс (Ванкувер, 1974)
• Восемнадцатый Конгресс (Хельсинки, 1978)
• Девятнадцатый Конгресс (Варшава, 1983)
• Двадцатый Конгресс (Беркли, 1986)

Двадцать первый Конгресс (Киото, 1990)

Международный Конференц-холл Киото

XXII — XXVII Конгрессы (1994—2014)

• Двадцать второй Конгресс (Цюрих, 1994)
• Двадцать третий Конгресс (Берлин, 1998)

• Двадцать четвёртый Конгресс (Пекин, 2002)
• Двадцать пятый Конгресс (Мадрид, 2006)
• Двадцать шестой Конгресс (Хайдарабад, 2010)
• Двадцать седьмой Конгресс (Сеул, 2014)

Немецкая почтовая марка, посвящённая Берлинскому Конгрессу

Структура современных конгрессов

Примерный список секций современного Конгресса:

• математическая логика и основания математики
• алгебра
• теория чисел
• геометрия
• топология
• алгебраическая геометрия
• комплексный анализ
• группы Ли и теория представлений
• вещественный и функциональный анализ
• теория вероятностей и математическая статистика

• дифференциальные уравнения с частными производными
• обыкновенные дифференциальные уравнения
• математическая физика
• численные методы и теория вычислений
• дискретная математика и комбинаторика
• математические аспекты информатики
• приложения математики к нефизическим наукам
• история математики
• преподавание математики