Многоугольники в спорте

Муниципальное бюджетное общеобразовательное учреждение

«Горская основная общеобразовательная школа»

Орехово-Зуевского муниципального района

Московской области

Реферат

по математике

на тему:

«Многоугольники в спорте»

Подготовил: ученик 7 класса

МБОУ «Горская ООШ»

Лапкин Павел

Руководитель: учитель

математики

Воронина Д.Ю.

2017г.

Содержание

1. Введение

2. Эволюция мячей Чемпионата Мира по футболу

3. Правильные многоугольники и многогранники

4. Мяч - математическая составляющая

5. Геодезический купол

6. Заключение

7. Использованная литература

Введение

Ни для кого не секрет, что чемпионат мира по футболу 2018 —пройдёт в России. Россия в первый раз в своей истории станет страной-хозяйкой мирового чемпионата по футболу, кроме того, он впервые будет проведён в Восточной Европе. Также в первый раз мундиаль состоится на территории двух частей света — Европы и Азии и впервые на территории бывшего Советского Союза. Проведение чемпионата запланировано на 12 стадионах в 11 городах России.

Неотъемлемой частью футбола является мяч. На каждом чемпионате, их всего было 20, изготавливался свой футбольный мяч. На сегодняшний день, говоря о футбольном мяче, мы представляем черно-белый мяч, состоящий из многоугольников.

Цель работы: изучить строение футбольного мяча.

Задачи работы:

• исследовать принцип построения макета для футбольного мяча;

• подробно изучить правильные многоугольники и многогранники;

• рассмотреть строение геодезического купола.

Объект исследования: футбольный мяч.

Эволюция мячей Чемпионата Мира по футболу

Приложение 1

Футбольный мяч состоит из трёх элементов: покрышка, подкладка, камера.

1. Покрышка 
   Изначально покрышка изготовлялась из натуральной кожи. Сейчас в основном применяют синтетику (полиуретан или поливинилхлорид), поскольку кожа впитывает воду и мяч набирает вес.

Большинство современных мячей состоят из 32 водонепроницаемых панелей, 12 из них имеют пятиугольную форму, 20 — шестиугольную. Панели футбольного мяча сшивают нитками ручным или машинным способом, или склеивают.

Первый такой мяч был произведён в Дании в 1950 году фирмой Select. Всемирно стал употребляться после чемпионата мира 1970 года, на котором были такие мячи, произведённые фирмой Адидас.

До этого употреблялся мяч, состоящий из 18 продолговатых частей и шнуровкой, по устройству похожий на современные волейбольные мячи. Эта конструкция достаточно распространена и до сих пор.

Финал чемпионата мира по футболу 2006 года в Германии был сыгран мячом Teamgeist. Впервые с 1970 года компания Adidas отступила от традиционной 32-панельной конфигурации покрышки и представила 14-панельный мяч.
Панели мяча были скреплены методом термального соединения.

Официальным мячом чемпионата мира по футболу в Южной Африке в 2010 году был Adidas Jabulani. Структура футбольного мяча состоит из 8 панелей, также скреплённых друг с другом термальным методом.

1. Подкладка 
   Внутренняя прослойка между покрышкой и камерой занимает подкладка. 
   Качество футбольного мяча напрямую зависит от толщины подкладки. Она влияет на качество отскока мяча и помогает сохранить его форму. Материалом для изготовления служит полиэстер или спрессованный хлопок. Современный профессиональный футбольный мяч состоит из четырёх и больше слоев подкладки.

2. Камера 
   Изготавливается из синтетического бутила или натурального латекса, иногда из полиуретана. Латексная камера сохраняет воздух менее продолжительное время, чем бутиловая. Но латексная камера имеет преимущество по сравнению с камерами, изготовленными из бутила или полиуретана по трём основным параметрам: мягкость, отскок и эластичность.

Параметры футбольного мяча:

• длина окружности не более 70 см (28 дюймов) и не менее 68 см (27 дюймов). 

• вес мяча не более 450 г (16 унций) и не менее 410 г (14 унций). 
  Масса указывается для сухого мяча.

• давление   —   0,6-1,1 атмосферы (600—1100 г/кв. см) на уровне моря.

Правильные многоугольники и многогранники

Многоугольник — это геометрическая фигура, ограниченная со всех сторон замкнутой ломаной линией, состоящая из трех и более отрезков (звеньев).

Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

Правильными называют многоугольники, у которых равны все стороны и все углы.

Многогранником называется трехмерное тело, граница которого состоит из многоугольников.

Правильным многогранником называется такой многогранник, у которого все грани равны и представляют собой равные правильные многоугольники.

В то время, как правильных многоугольников существует сколько угодно, правильных многогранников ограниченное число.

Рассмотрим возможные правильные многогранники и прежде всего те из них, гранями которых являются правильные треугольники. Наиболее простым таким правильным многогранником является треугольная пирамида, гранями которой являются правильные треугольники (рис. 1,а). В каждой ее вершине сходится по три грани. Имея всего четыре грани, этот многогранник называется также тетраэдром, что в переводе с греческого языка означает четырехгранник.

Многогранник, гранями которого являются правильные треугольники, и в каждой вершине сходится четыре грани, изображен на рисунке 1,в. Его поверхность состоит из восьми правильных треугольников, поэтому он называется октаэдром.

Многогранник, в каждой вершине которого сходится пять правильных треугольников, изображен на рисунке 1,г. Его поверхность состоит из двадцати правильных треугольников, поэтому он называется икосаэдром. 
Заметим, что поскольку в вершинах выпуклого многогранника не может сходиться более пяти правильных треугольников, то других правильных многогранников, гранями которых являются правильные треугольники, не существует. 
Аналогично, поскольку в вершинах выпуклого многогранника может сходиться только три квадрата, то, кроме куба (рис. 1,б), других правильных многогранников, у которых гранями являются квадраты не существует. Куб имеет шесть граней и поэтому называется также гексаэдром. 
Многогранник, гранями которого являются правильные пятиугольники, и в каждой вершине сходится три грани, изображен на рисунке 1,д. Его поверхность состоит из двенадцати правильных пятиугольников, поэтому он называется додекаэдром. 

Правильные многогранники с древних времен привлекали к себе внимание ученых, строителей, архитекторов и многих других. Их поражала красота, совершенство, гармония этих многогранников. Пифагорейцы считали эти многогранники божественными и использовали их в своих философских сочинениях о существе мира. Они считали, что элементы первооснов бытия имеют форму правильных многогранников, а именно: огонь – тетраэдр; земля - гексаэдр; воздух – октаэдр; вода – икосаэдр; вся Вселенная, по мнению древних, имела форму додека­эдра. Подробно описал свойства правильных многогранников древнегреческий ученый Платон. Именно поэтому правильные многогранники называются также телами Платона. Правильным многогранникам посвящена последняя XIII книга знаменитых "Начал" Евклида.

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы, архитекторы, художники. Леонардо да Винчи, например, увлекался теорией многогранников и часто изображал их на своих полотнах. Он проиллюстрировал изображениями правильных и полуправильных многогранников книгу своего друга монаха Луки Пачоли (1445-1514) "О божественной пропорции".

Другим знаменитым художником эпохи Возрождения, также увлекавшимся геометрией, был А. Дюрер. В его известной гравюре "Меланхолия" на переднем плане изображен додекаэдр. В 1525 году Дюрер написал трактат, в котором представил пять правильных многогранников, поверхности которых служат хорошими моделями перспективы.

Иоганн Кеплер (1571-1630) в своей работе "Тайна мироздания" в 1596 году, используя правильные многогранники, вывел принцип, которому подчиняются формы и размеры орбит планет Солнечной системы. Геометрия Солнечной системы, по Кеплеру, заключалась в следующем: "Земля (имеется в виду орбита Земли) есть мера всех орбит. Вокруг сферы Земли опишем додекаэдр. Описанная вокруг додекаэдра сфера есть сфера Марса. Вокруг сферы Марса опишем тетраэдр. Описанная вокруг тетраэдра сфера есть сфера Юпитера. Вокруг сферы Юпитера опишем куб. Описанная вокруг куба сфера есть сфера Сатурна. В сферу Земли вложим икосаэдр. Вписанная в него сфера есть сфера Венеры. В сферу Венеры вложим октаэдр. Вписанная в него сфера есть сфера Меркурия". Такая модель Солнечной системы получила название "Космического кубка" Кеплера (рис. 2)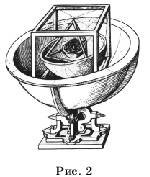

Мяч - математическая составляющая

Поверхность классического футбольного мяча состоит из «слегка искривлённых» 12 правильных пятиугольников чёрного цвета и 20 правильных белых шестиугольников. Модель мяча можно представить следующим образом.

Из 12 правильных пятиугольников и 20 правильных шестиугольников с равными сторонами можно сложить многогранник, называемый усечённым икосаэдром.

Икосаэдр — один из пяти правильных многогранников. Его название происходит от древнегреческих слов -двадцать, -основание. У икосаэдра 12 вершин, 20 граней — правильных треугольников, 30 рёбер.«Отрежем» (отсечём) вершины икосаэдра, отступив от вершин вдоль прямых, направленных в центр, на столько, чтобы оставшиеся части граней были правильными шестиугольниками. Очевидно, что срезы будут правильными пятиугольниками. Получившаяся фигура и есть усечённый икосаэдр.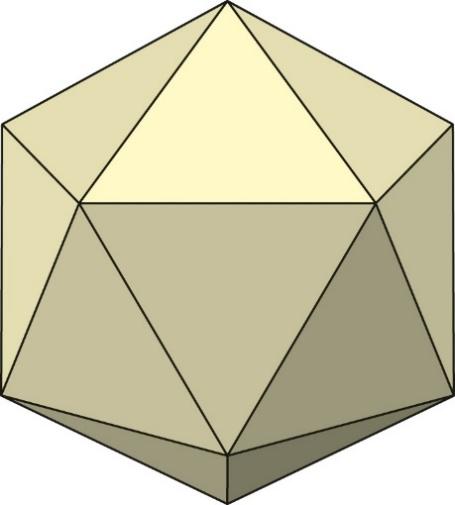

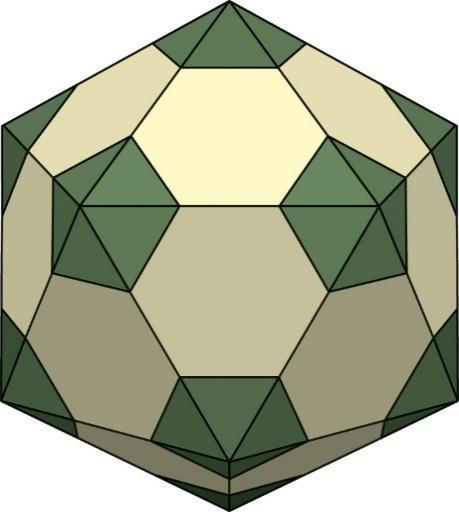
Усечённый икосаэдр — один из полуправильных многогранников. Так называются многогранники, у которых все грани — правильные многоугольники нескольких разных типов (в отличие от правильных многогранников, все грани которых — одинаковые правильные многоугольники), а все вершины устроены «одинаково», т. е. многогранные углы при вершинах равны (совместимы).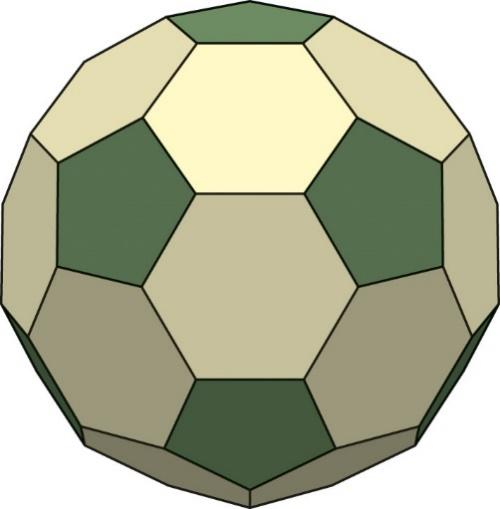

При «наполнении воздухом» усечённого икосаэдра он принимает форму сферы, становится футбольным мячом. При этом вершины усечённого икосаэдра совпадут с «вершинами мяча», рёбра перейдут в швы, а грани — в «слегка искривлённые» многоугольники на поверхности мяча. Таким образом получится модель мяча — центральная проекция усечённого икосаэдра на сферу.

Геодезический купол

Геодезический купол — сферическое архитектурное сооружение, собранное из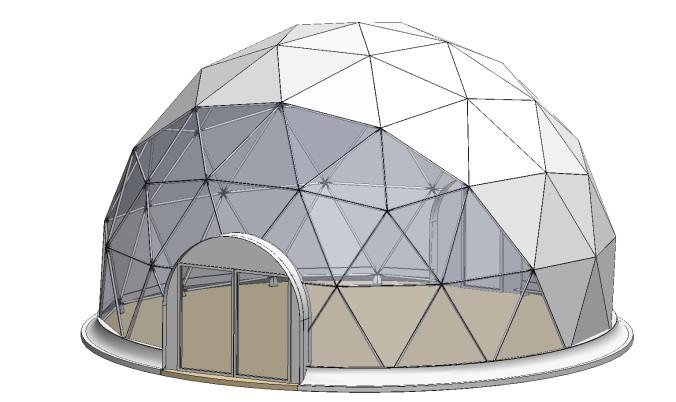

стержней, образующих геодезическую структуру, благодаря которой сооружение в целом обладает хорошими несущими качествами. Геодезический купол является несущей сетчатой оболочкой. Построение купола основано так же, как и футбольный мяч на икосаэдре.

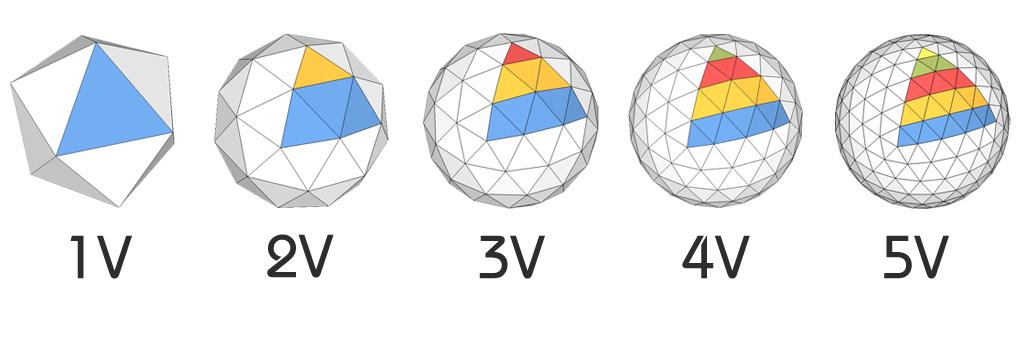
Для начала мы строим сферу с заданным радиусом. Далее мы строим икосаэдр «вписанный» в сферу. В этом случае все 12 вершин икосаэдра лежат на поверхности сферы. Все треугольники равны.

Т.к. все треугольники в икосаэдре равны, мы выбираем любой из них и разбиваем его на более мелкие равносторонние треугольники расположенные рядами. Так получается «плоская» разбивка сетки. Далее строим отрезки исходящие из центра сферы. Эти отрезки должны проходить через точки соединения получившейся сетки и заканчиваться на поверхности сферы. В итоге соединяем все вершины отрезков, лежащие теперь на поверхности сферы. У нас получилась структура из треугольников, вершины которых лежат на поверхности сферы, практически повторяя ее форму. Т.к. все изначальные треугольники икосаэдра одинаковые, то мы можем смело копировать нашу получившуюся сетку, получая желаемый геодезический купол или сферу.

Заключение

Интересно и то, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Вирус не может быть совершенно круглым, как считалось ранее. Чтобы установить его форму, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр. Его геометрические свойства, о которых говорилось выше, позволяют экономить генетическую информацию. Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется.

Многогранники окружают нас повсюду: детские кубики, мебель, архитектурные сооружения и т. п. В повседневной жизни мы почти перестали их замечать, а ведь это очень интересно, знать историю привычных для всех предметов, тем более, если она так увлекательна.

Использованная литература

1. Смирнова И., Смирнов В. Что такое «Полуправильный многогранник» //Учебно-методическая газета «Математика» - 2007.-№16-с.23-26

2. Смирнова И.М. В мире многогранников: Кн. Для учащихся - М.: Просвещение, 1995.

3. Литвиненко В.Н. Многогранники. Задачи и решения: - М.: Вита-Пресс, 1995.

4. Долбилин Н.П. Жемчужины теории многогранников. – М.: МЦНМО, 2000, с.27-31. 

5. Люстерник Л.А. Выпуклые фигуры и многогранники. – М.; 1956. 

6. Энциклопедия элементарной математики. Книга IV. Геометрия. - М.; 1963, с. 382. 

7. http://school-collection.edu.ru/catalog/res/14d279ca-eec5-53a8-6248-07861c51eed4/?fullView=1

8. http://alexfl.ru/vechnoe/vechnoe_garmon1.html

9. http://www.ansmed.ru/books/elektronnaya-enciklopediya-narodnoy-mediciny/chast-13-prostranstvo-dlya-zhizni/energetika-0

10. http://book.etudes.ru/toc/football/

11. http://strmnt.com/sad/l-diz/postrojki/geodezicheskij-kupol.html