Многоугольники и их площади. Формула Пика

Отдел образования администрации Куженерского муниципального района МБОУ «Конганурская средняя общеобразовательная школа»

VI республиканские «Яналовские чтения»,

посвященные Году искусства и культурного наследия

Конкурс проектно-исследовательских работ

Секция физико-математическая

Многоугольники и их площади.

Формула Пика

Выполнил: Тобеков Алексей, обучающаяся 8 класса МБОУ «Конганурская средняя общеобразовательная школа»

Куженерского муниципального района.

Руководитель: Войкова Роза Ефимовна, учитель математики

МБОУ «Конганурская средняя общеобразовательная школа»

Куженерского муниципального района

д. Большой Тумьюмучаш, 2022г.

Математике должно учить еще с той целью,

чтобы познания здесь приобретаемые,

были достаточными для обыкновенных

потребностей жизни».

Н.И.Лобачевский.

Цель исследовательской работы:

Научиться применять формулу Пика для нахождения площадей фигур, расположенных на решётке, и определить рациональность её применения.

Задачи:

• Подробнее познакомиться с формулой Пика;
• Проанализировать и систематизировать полученную информацию;
• Найти различные методы и рациональные приемы решения задач на нахождение площади многоугольника на клетчатой бумаге;

• Подобрать задачи, где можно использовать эту формулу и решить их двумя способами (по формуле нахождения площади и по формуле Пика);

• Создать презентацию работы для представления собранного материала одноклассникам.

Объект исследования:  формула Пика

Предмет исследования:  применение формулы Пика при решении задач на нахождение площади фигур, изображённых на клетчатой бумаге.

Гипотеза:

Верно ли, что площадь фигуры, вычисленная по формуле Пика равна площади фигуры, вычисленной по формуле из учебника геометрии?

Актуальность данного исследования состоит в том, что усвоение формулы может помочь школьникам, а особенно сдающим ОГЭ и ЕГЭ, быстро и легко решать задачи на вычисление площади различных фигур на клетчатой бумаге.

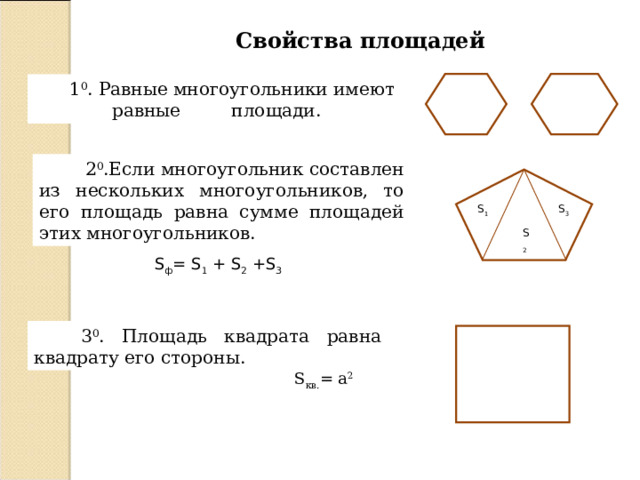
Свойства площадей

1 0 . Равные многоугольники имеют равные площади.

2 0 .Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.

S 1

S 3

S 2

S ф = S 1 + S 2 + S 3

3 0 . Площадь квадрата равна квадрату его стороны.

S кв. = a 2

Формулы площадей плоских фигур

Актуализация знаний.

Давайте повторим основные формулы нахождения площадей, которые нам пригодятся сегодня на уроке.

Необходимо нажать на формулу маркером от интерактивной доски для проверки.

Георг Александр Пик

(10.09.1859 - 13.07.1942)

• Георг Александр Пик (10.09.1859 - 13.07.1942)

В шестнадцать лет Георг окончил школу, сдал выпускные экзамены и поступил в Венский университет.

В двадцать лет получил право преподавать физику и математику.

16 апреля 1880 года под руководством Лео Кёнигсберг ёра Пик защитил докторскую диссертацию «О классе абелевых интегралов».

В 1881 году он получил место ассистента у Эрнста Маха, который занял кафедру физики в Пражском университете.

Георг Александр Пик

(10.09.1859 - 13.07.1942)

• Георг Александр Пик (10.09.1859 - 13.07.1942)

В 1884 году Пик уехал в Лейпцигский университет к Феликсу Клейну. Там он познакомился с другим учеником Клейна, Давидом Гильбертом.

Позже, в 1885 году, он вернулся в Прагу, где и прошла оставшаяся часть его научной карьеры.

В июле 1942 года, в возрасте 82 года Георг был депортирован нацистами в лагерь Терезиенштадт, где вскоре умер.

Использование формулы для нахождения площадей фигур на решётчатой бумаге

Теорема: Площадь многоугольника с целочисленными вершинами равна В+Г/2 - 1, где

В- количество целочисленных узлов внутри многоугольника, а

Г - количество целочисленных узлов на границе многоугольника.

Например, для многоугольника, изображенного на рисунке:

В=10 (количество внутренних узлов),

Г=5 (количество граничных узлов), Значит, площадь многоугольника равна

S = 10 + 5/2 – 1=11,5

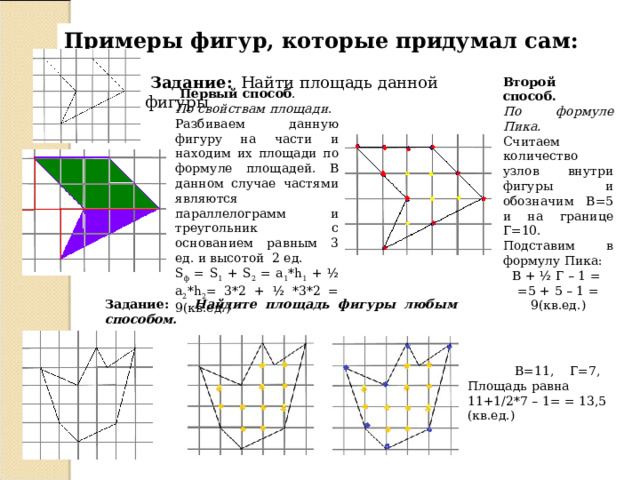
Примеры фигур, которые придумал сам:

h 1

Первый способ .

По свойствам площади .

Разбиваем данную фигуру на части и находим их площади по формуле площадей. В данном случае частями являются параллелограмм и треугольник с основанием равным 3 ед. и высотой 2 ед.

S ф = S 1 + S 2 = a 1 *h 1 + ½ a 2 *h 2 = 3*2 + ½ *3*2 = 9( кв . ед .)

Задание: Найти площадь данной фигуры

Второй способ.

По формуле Пика.

Считаем количество узлов внутри фигуры и обозначим В=5 и на границе Г=10. Подставим в формулу Пика:

В + ½ Г – 1 =

=5 + 5 – 1 = 9(кв.ед.)

Задание: Найдите площадь фигуры любым способом.

В=11, Г=7,

Площадь равна 11+1/2*7 – 1= = 13,5 (кв.ед.)

Задачи для подготовки к ОГЭ и ЕГЭ

Эксперимент, проведённый в 9-х и 11 классе

Вычислить площадь фигуры.

Сравнительный анализ верно выполненных заданий и времени, затраченного на решение задач учащимися 9 и 11 класса

Задания

Геометрический способ

Решение

время

По формуле Пика

Решение

Время

Верно решили по формулам геометрии

Верно решили по формулам геометрии

Верно решили по формуле Пика

Верно решили по формуле Пика

7

8

Среднее время, затраченное на решение по формулам геометрии

8

9

7

9

Среднее время, затраченное на решение по формулам геометрии

3мин 51сек

9

8

Среднее время, затраченное на решение по формуле Пика

Среднее время, затраченное на решение по формуле Пика

7

9

4мин 5сек

9

2мин20сек

7

1мин8сек

2мин 42сек

2мин

15сек

9

6

9

10

4мин

1мин7сек

1мин15сек

3мин

42сек

1мин 53сек

3мин

58сек

4мин 50с.

2мин 3сек

1мин58сек

1мин36сек

Заключение

Выполняя работу, подробно познакомился с формулой Пика для измерения площадей любого многоугольника на клетчатой бумаге.

Чтобы вычислить площадь фигуры на клетчатой бумаге пользуемся формулой Пика: S = В + Г/2 – 1.

Проверена справедливость этой формулы для нахождения площадей многоугольников.

В работе представлены 15 задач, решенные двумя способами: по формуле Пика и основным формулам площадей.

Некоторые из них легче решить по обычным формулам, так как площади квадрата, прямоугольника и прямоугольного треугольника знает каждый ученик.

Итак, проще получилось вычислить площадь фигуры по формуле Пика, т.к. подсчитать целочисленные узлы намного легче, чем дорисовывать (дополнять) рисунки до прямоугольников или квадратов.

Задачи выполнены, цель достигнута.

Список литературы

• Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7-9 классы: учеб. для общеобразоват. организации - 6-е изд. - М.: Просвещение, 2016. - 383с.

• Лысенко Ф.Ф., Кулабухова С.Ю. Математика. 9-й класс. Подготовка к ГИА-2018: учебно-методическое пособие. Ростов-на- Дону: Легион, 2018. - 304 с.
• Лысенко Ф.Ф., Кулабухова С.Ю. Математика. Подготовка к ЕГЭ- 2018. Книга 1:Ростов-на-Дону: Легион, 2018. - 352с.
• Математика. Все для учителя! № 3, 2013г.
• Открытый банк заданий ЕГЭ по математике, http :// mathege . ru / or / ege / Main
• Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия: учебное пособие для учащихся 5-6 классов. - М.: МИРОС, 1995. - 240с.
• Штейнгауз Г. Математический калейдоскоп: пер. с польского. — М. : Наука. Главная ре­дакция физико-математической литературы, 1981 (Серия: Библиотечка «Квант»).
• Ященко И.В. Математика: типовые экзаменационные варианты: 36 вариантов - М.: Издательство «Национальное образование», 2018. - 240 с. - (ОГЭ, ФИПИ - школа).
• http :// ru . wikipedia . org / .
• https://ege.sdamgia.ru/test?theme=190
• http://yspu.org/Методические_журналы