Просмотр содержимого документа
«Множество действительных чисел»

МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

Если множество рациональных чисел дополнить множеством иррациональных чисел, то вместе они составят множество действительных чисел
Это множество конечных и бесконечных десятичных дробей
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

Каждое действительное число можно
изобразить точкой на координатной прямой.
Каждая точка координатной прямой имеет действительную координату.
Между множеством R действительных чисел и множеством точек координатной прямой установлено взаимно-однозначное соответствие.
Координатная прямая есть геометрическая модель множества действительных чисел; по этой причине для координатной прямой часто используют термин числовая прямая.
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU
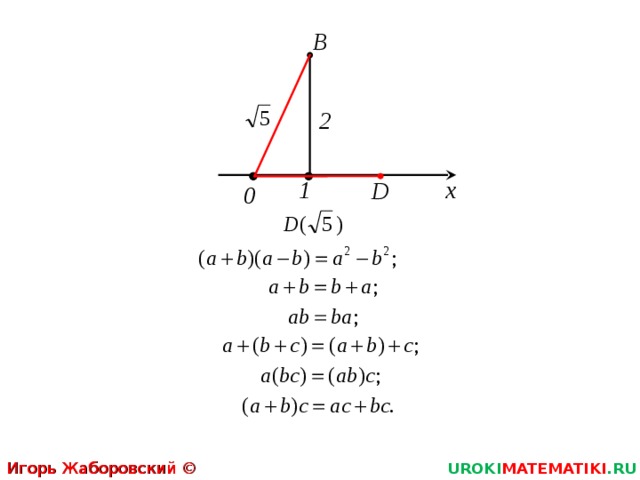
B
2
x
1
D
0
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

Произведение (частное) двух положительных чисел — положительное число
Произведение (частное) двух отрицательных чисел — положительное число
Произведение (частное) положительного и отрицательного чисел — отрицательное число
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU
 b ( a ). Всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b – 0 = b — отрицательное число). а 0 а – положительное число а – отрицательное число а 0 а- b – положительное число, т.е. a-b0 а b а а- b – отрицательное число, т.е. a-b Игорь Жаборовский © 2012 UROKI MATEMATIKI .RU " width="640"
b ( a ). Всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b – 0 = b — отрицательное число). а 0 а – положительное число а – отрицательное число а 0 а- b – положительное число, т.е. a-b0 а b а а- b – отрицательное число, т.е. a-b Игорь Жаборовский © 2012 UROKI MATEMATIKI .RU " width="640"
Определение. Действительное число а больше (меньше) действительного числа b , если их разность a-b — положительное (отрицательное) число. Пишут: ab ( a ).
Всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b – 0 = b — отрицательное число).
а 0
а – положительное число
а – отрицательное число
а 0
а- b – положительное число, т.е. a-b0
а b
а
а- b – отрицательное число, т.е. a-b
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

а больше нуля или равно нулю, т.е. а — неотрицательное число (положительное или 0), или что а не меньше нуля;
а меньше нуля или равно нулю, т.е. а — неположительное число (отрицательное или 0), или что а не больше нуля;
а больше или равно b , т.е. а - b — неотрицательное число, или что а не меньше b ;
а меньше или равно b , т.е. а - b — неположительное число, или что а не больше b ;
Из двух чисел а , b больше то, которое
располагается на числовой прямой правее.
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

Пример 1: Сравнить числа:
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU

Пример 1: Сравнить числа:
Пример 2 : Расположить в порядке возрастания числа:
Игорь Жаборовский © 2012
UROKI MATEMATIKI .RU










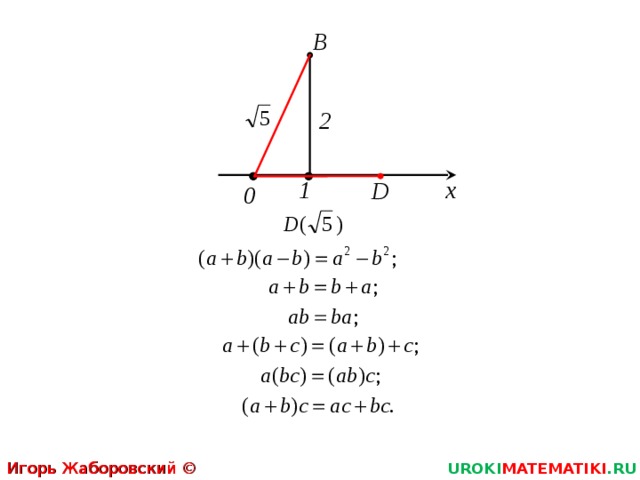

 b ( a ). Всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b – 0 = b — отрицательное число). а 0 а – положительное число а – отрицательное число а 0 а- b – положительное число, т.е. a-b0 а b а а- b – отрицательное число, т.е. a-b Игорь Жаборовский © 2012 UROKI MATEMATIKI .RU " width="640"
b ( a ). Всякое положительное число а больше нуля (поскольку разность а - 0 = а — положительное число), а всякое отрицательное число b меньше нуля (поскольку разность b – 0 = b — отрицательное число). а 0 а – положительное число а – отрицательное число а 0 а- b – положительное число, т.е. a-b0 а b а а- b – отрицательное число, т.е. a-b Игорь Жаборовский © 2012 UROKI MATEMATIKI .RU " width="640"













