Модели на графах. Решение задач. 9 класс

Предмет: Информатика и ИКТ

Класс: 9

Тема урока: Решении задач, с использованием моделей на графах

Базовый учебник: Информатика и ИКТ: учебник для 9 класса Л. Л. Босова, А. Ю. Босова.

Цель урока: применение знаний по теме «Информационные модели на графах» на практике.

Задачи урока:

• Образовательные:

систематизировать и расширить представление учащихся о графах;

научить применять полученные знания на практике, оперировать имеющимся потенциалом в конкретной ситуации;

продолжить формирование познавательного интереса к информатике.

• Воспитательные:

вовлечь в активную деятельность;

формировать культуру;

совершенствовать навыки общения.

• Развивающие:

развивать логическое мышление, способность к анализу и синтезу;

развивать находчивость, умения преодолевать трудности при решении нестандартных задач;

развивать творческие способности;

развивать коммуникативные навыки работы в группах;

Тип урока применения знаний на практике.

Формы работы учащихся

• фронтальная работа;

• групповая форма работы.

Используемые технологии, активные формы обучения

• технология дифференцированного обучения (задания разного уровня);

• игровая технология;

• технология концентрированного обучения. В процессе совместной работы ученики учат друг друга. Лучшему усвоению материала способствует взаимное обучение, так как ученики усваивают 90% от того, чему учат сами. 

• здоровье сберегающая технология, так как использование дидактических игр дает возможность ученикам не только успешнее усваивать материал, но и отдохнуть. 

• информационно-коммуникационные технологии.

Необходимое техническое оборудование

• персональный компьютер учителя;

• мультимедийный проектор;

• экран.

Структура и ход (конспект) урока

Решить задачу:

Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

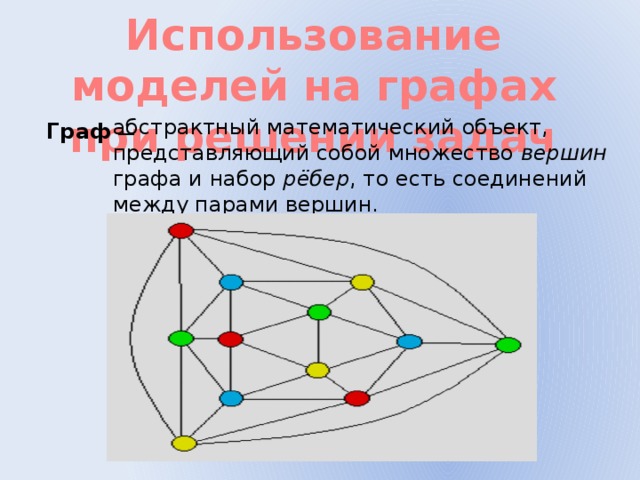
Использование моделей на графах при решении задач

абстрактный математический объект, представляющий собой множество вершин графа и набор рёбер , то есть соединений между парами вершин.

Граф   —

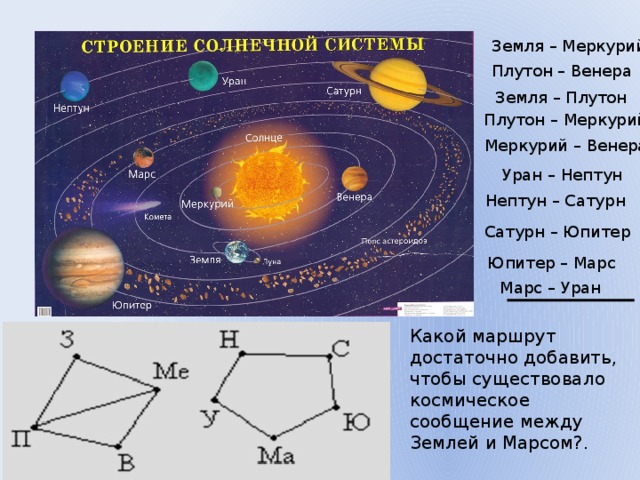
Земля – Меркурий

Плутон – Венера

Земля – Плутон

Плутон – Меркурий

Меркурий – Венера

Уран – Нептун

Нептун – Сатурн

Сатурн – Юпитер

Юпитер – Марс

Марс – Уран

Какой маршрут достаточно добавить, чтобы существовало космическое сообщение между Землей и Марсом?.

Граф и его элементы

Ориентированные графы

Задание 1

Задание 50

Взвешенные графы

100

Задание 2

Задание 1

Задание 3

200

Задание 2

Связные и несвязные графы

50

Деревья

300

Задание 2

Задание 3

200

Задание 1

400

200

Задание 3

100

Задание 1

Задание 2

50

300

Задание 3

200

Задание 2

400

200

Задание 3

300

Ориентированные графы

Задание № 1:

Какой граф называется ориентированным?

Как называются ребра в ориентированном графе?

начало

Ориентированные графы

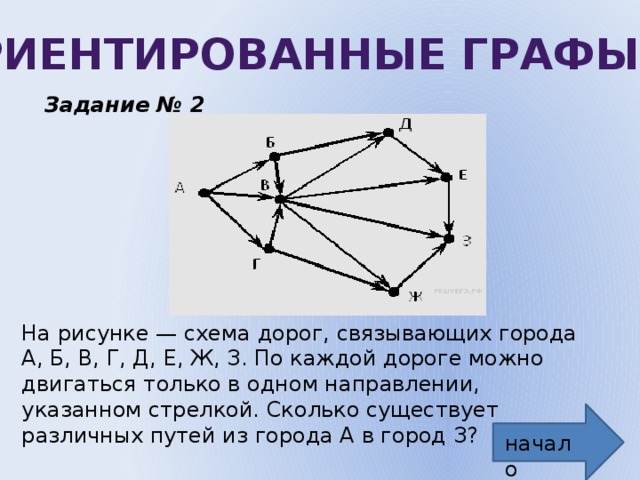
Задание № 2

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город З?

начало

Ориентированные графы

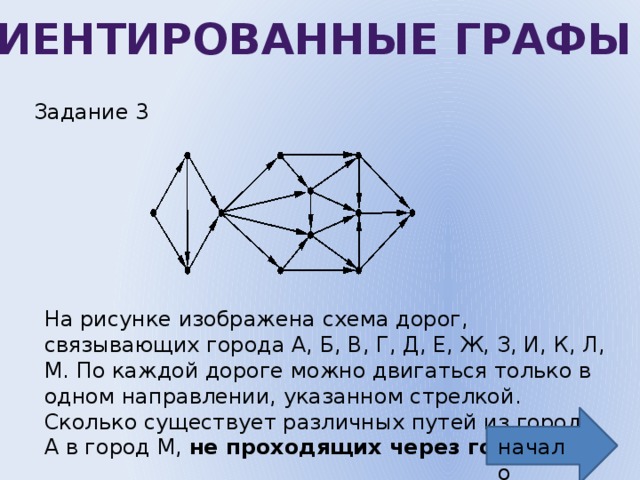
Задание 3

На рисунке изображена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, не проходящих через город Е ?

начало

Взвешенные графы

Задание № 1

Какой граф называется взвешенным?

Что может обозначать вес?

начало

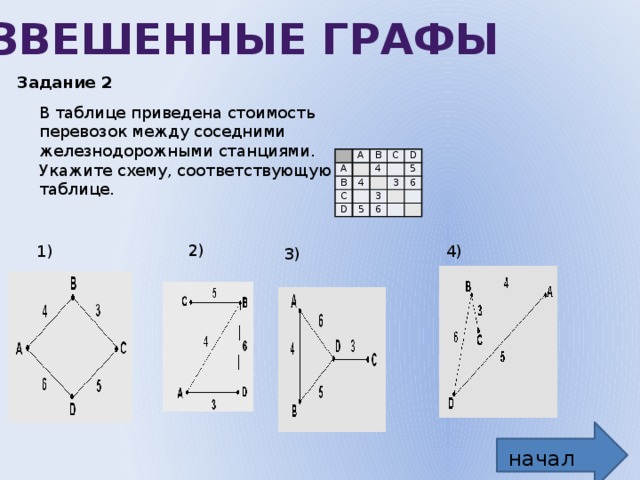
Взвешенные графы

Задание 2

В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите схему, соответствующую таблице.

A

A

B

B

4

C

4

C

D

D

3

5

5

3

6

6

2)

1)

4)

3)

начало

Взвешенные графы

Задание 3

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).

A

A

B

B

C

C

4

4

D

D

E

6

6

E

F

3

F

3

6

6

4

4

2

2

5

5

начало

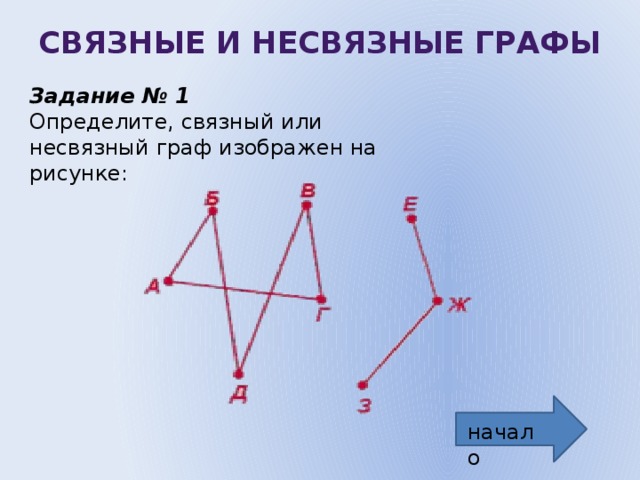
Связные и несвязные графы

Задание № 1

Определите, связный или несвязный граф изображен на рисунке:

начало

Связные и несвязные графы

Задание № 2

Нарисуйте граф , в котором 5 вершин и 3 компоненты связности. Сколько существует разных графов, удовлетворяющих условию задачи?

начало

Связные и несвязные графы

Задание № 3

• В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией в том и только в том случае, если двузначное число, образованное названиями городов, делится на 3. Можно ли долететь по воздуху из города 1 в город 9 ?

начало

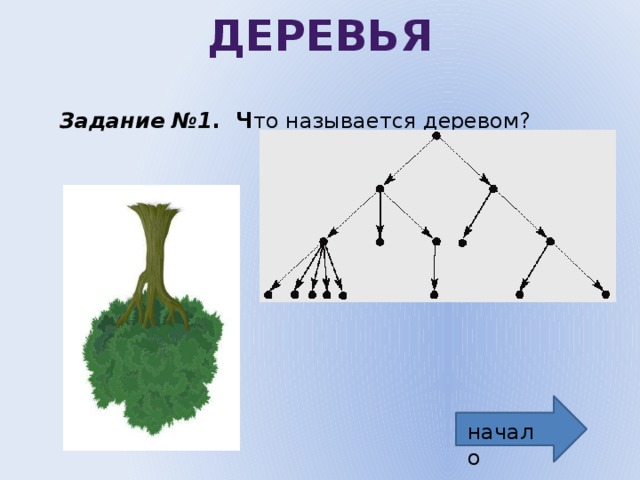
Деревья

Задание №1 . Ч то называется деревом?

начало

Деревья

Задание №2 . Для отправки поздравления есть конверты трех видов, на которые клеится одна из двух марок и в которые вкладывается одна из четырех открыток. Сколько существует способов сделать поздравления по почте?

начало

Деревья

Задание №2.

Сколькими способами можно рассадить в ряд на три стула трех учеников? Выписать все возможные случаи.

начало

Деревья

Задание 3. Квартет.

« Проказница мартышка, осел, козел да косолапый мишка затеяли сыграть в квартет». Мартышка расположилась напротив медведя, а слева и справа от нее – осел и козел. «Ударили в смычки, дерут, а толку нет». Тогда осел и козел поменялись местам. «Расселись, начали квартет. Он все-таки на лад нейдет». Таким образом, они перепробовали все возможные вариант. Медведь всегда оставался на одном месте. Сколько всего было вариантов расположения незадачливых музыкантов?

начало

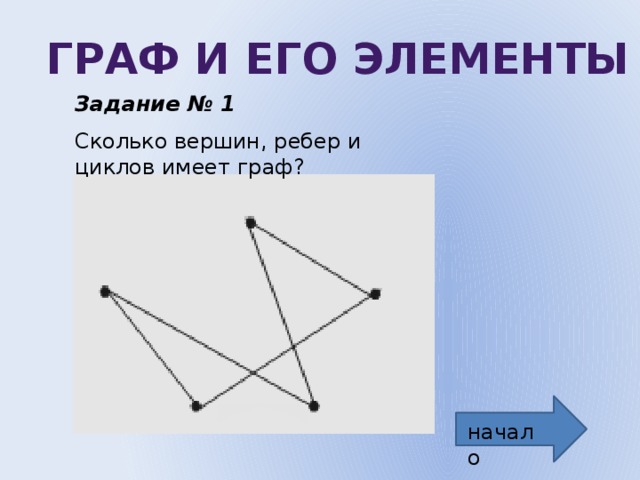
Граф и его элементы

Задание № 1

Сколько вершин, ребер и циклов имеет граф?

начало

Граф и его элементы

Задание №2

Изобразите с помощью графа договорные отношения между предприятиями А, Б, В, Г, Д, Е, если к рассматриваемому моменту:

предприятие А установило договорные отношения со всеми другими предприятиями;

Б установило с Г и Д;

В установило со всеми предприятиями, кроме предприятия Е.

Сколько вершин и сколько ребер имеет полученный граф?

начало

Граф и его элементы

Задание №3

Среди семи стран установлены экономические отношения, причем каждая страна имеет экономические договоры с каждой другой страной. Изобразите в виде графа результат установленных экономических отношений. Сколько ребер имеет полученный граф?

начало