Модели оптимального планирования

Модели оптимального планирования

Процесс постановки и решения задач оптимизации можно представить в виде взаимосвязанных этапов, на которых выполняются определенные действия:

• осмысление задачи, выделение наиболее важных

качеств, свойств, величин, параметров;

• введение неизвестных;
• создание целевой функции;
• составление системы ограничений;
• решение задачи на компьют ере

Постановка задачи: «Оптимизация перевозки».

Построить формальную модель «Оптимизация перевозки» перевозки компьютерного класса, состоящего из 15 компьютеров, с использованием единственного легкового автомобиля. Каждый компьютер упакован в две коробки (монитор и системный блок) и существует три варианта погрузки коробок в автомобиль:

Тип коробки

Варианты погрузки

Монитор

1

Системный блок

2

3

3

2

1

1

2

4

Формальная модель

Параметрами, значения которых требуется определить, являются количества рейсов автомобиля, загруженного различными способами:

• Х 1 – количество рейсов автомобиля, загруженного по варианту 1 ;
• Х 2 – количество рейсов автомобиля, загруженного по варианту 2 ;
• Х 3 – количество рейсов автомобиля, загруженного по варианту 3 ;
• Тогда целевая функция, равная количеству рейсов автомобиля, примет вид:
• F = Х 1 + Х 2 + Х 3

Оптимальным планом будет определение значений параметров с учетом ограниченности ресурсов при достижении стратегической цели.

Цель – минимальное количество рейсов автомобиля.

Составление системы ограничений

• Ограничения накладываются количествами коробок с мониторами и системными блоками, которые необходимо перевести. Должны выполняться два равенства:
• 3∙Х 1 + 2∙Х 2 + 1∙Х 3 = 15
• 1∙Х 1 + 2∙Х 2 + 4∙Х 3 = 15
• Кроме того, количества рейсов не могут быть отрицательными, поэтому должны выполняться неравенства:
• Х 1  0; Х 2  0; Х 3  0

Система ограничений

3∙Х 1 + 2∙Х 2 + 1∙Х 3 = 15 ;

1∙Х 1 + 2∙Х 2 + 4∙Х 3 = 15 ;

Х 1  0;

Х 2  0;

Х 3  0 ;

Компьютерная модель «Оптимизация перевозки» в электронных таблицах Microsoft Excel.

• 1.Ячейки B 2, C 2 и D 2 выделить для хранения значений параметров X 1, X 2 и X 3.
• В ячейку B 4 ввести формулу вычисления целевой функции: =B2+C2+D2.
• В ячейку B 7 ввести формулу вычисления количества коробок с мониторами:
• =3*B2+ 2*C2 + 1*D2
• В ячейку B 8 ввести формулу вычисления количества коробок с системными блоками:
• =1*B2+ 2*C2 + 4*D2

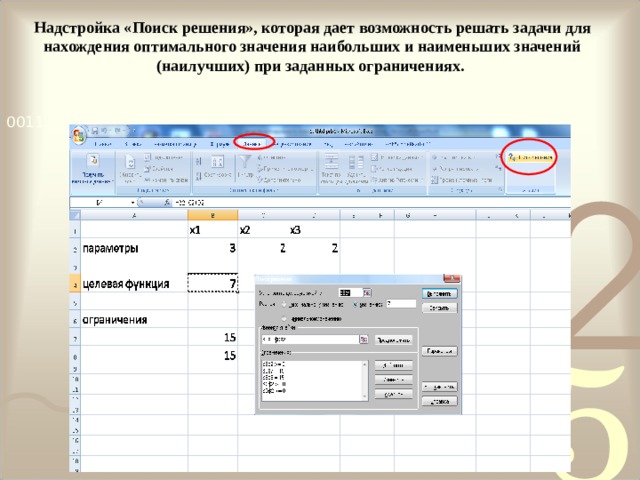
Надстройка «Поиск решения», которая дает возможность решать задачи для нахождения оптимального значения наибольших и наименьших значений (наилучших) при заданных ограничениях.

• Задание: Дома решить задачу на компьютере описанную в учебнике §39 . Требуется найти число пирожков и пирожных, чтобы обеспечить максимальную выручку кондитерскому цеху, только с немного

измененным условием : число пирожных должно быть не меньше числа пирожков.

Семакин И.Г. Хеннер Е.К.. Информатика и ИКТ 10-11 кл., §39

Используемая литература

• И.Г.Семакин и др. Информатика 10-11. Практикум, М.: Бином. Лаборатория знаний, 2012
• И.Г.Семакин и др. Информатика 10-11. Базовый уровень, М.: Бином. Лаборатория знаний, 2013