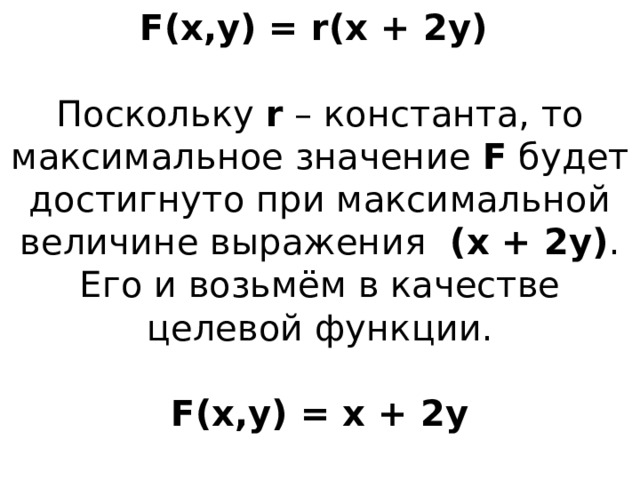Модели оптимального планирования

Модели оптимального планирования

Постановка задачи планирования

• Имеются некоторые плановые показатели: X, Y и др.;
• Имеются некоторые ресурсы: R1, R2 и др., за счёт которых эти плановые показатели могут быть достигнуты. Эти ресурсы практически всегда ограничены;
• Имеется определённая стратегическая цель, зависящая от значений X, Y и др. плановых показателей, на которую следует ориентировать планирование;
• Нужно определить значение плановых показателей X, Y и др. с учётом ограниченности ресурсов R1, R2 и др. при условии достижения стратегической цели. Это и будет оптимальным планом.

Примеры

Объект планирования: ДЕТСКИЙ САД

• Плановые показатели:

• Количество детей Количество воспитателей
• Количество детей
• Количество воспитателей
• Ресурсы: Объём финансирования Площадь помещения
• Объём финансирования
• Площадь помещения
• Стратегическая цель: сохранение и укрепление здоровья детей. Количественной мерой цели является минимизация заболеваемости детей.

Задача:

Школьный кондитерский цех готовит пирожки и пирожные. В силу ограниченности ёмкости склада за день можно приготовить не более 700 штук изделий. Рабочий день длится 8 часов. За день можно произвести 1000 штук пирожков, если при этом не производить пирожных. Производство пирожных более трудоёмко и их можно произвести не более 250 штук. Стоимость пирожного вдвое выше стоимости пирожка. Требуется составить такой дневной план производства , чтобы обеспечить наибольшую выручку кондитерского цеха.

Объект планирования: Кондитерский цех

• Плановые показатели:

• X – дневной план выпуска пирожков Y – дневной план выпуска пирожных
• X – дневной план выпуска пирожков
• Y – дневной план выпуска пирожных
• Ресурсы: Длительность рабочего дня – 8 часов Вместимость складского помещения – 700 мест
• Длительность рабочего дня – 8 часов
• Вместимость складского помещения – 700 мест
• Стратегическая цель: получение максимальной выручки.

= 0 и y = 0 Если мы хотим использовать компьютер для решения задачи, то нам нужно построить мат.модель! " width="640"

Формализация

• Х + Y
• Время изготовления пирожка t минут
• Время изготовления пирожного 4t минут
• Суммарное время изготовления х пирожков и y пирожных не больше 8 часов или 480 минут tx + 4ty = t(x + 4y)
• За рабочий день можно сделать 1000 пирожков, значит t = 480 / 1000 = 0,48 мин. Подставим 0,48(x + 4y) x + 4y
• Количество пирожков и пирожных не может быть отрицательным, т.е. х = 0 и y = 0

Если мы хотим использовать компьютер для решения задачи, то нам нужно построить мат.модель!

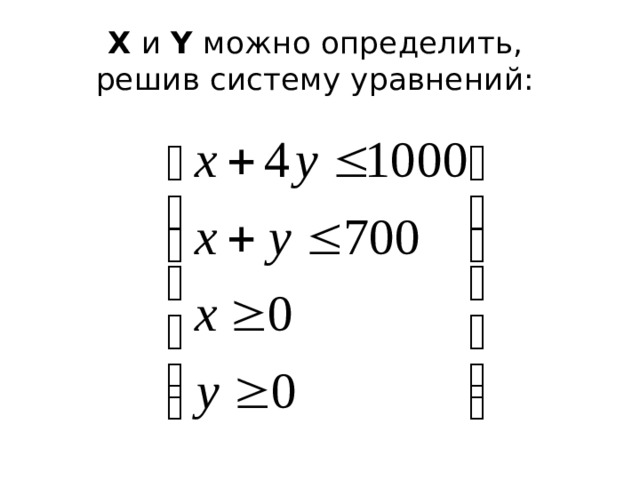
X и Y можно определить, решив систему уравнений:

Формализация цели (max выручка):

• Выручка − это стоимость проданной продукции
• Пусть цена одного пирожка r рублей
• Тогда цена одного пирожного 2r рублей
• Стоимость всей произведённой за день продукции равна rx + 2ry = r(x + 2y)
• Получили целевую функцию F(x,y) = r(x + 2y)
• Требуется решить систему уравнений и взять из решения такие х и y при которых значение целевой функции будет максимальным.
• Математическая дисциплина, которая посвящена решению таких задач называется линейным программированием .

Если мы хотим использовать компьютер для решения задачи, то нам нужно построить мат.модель!

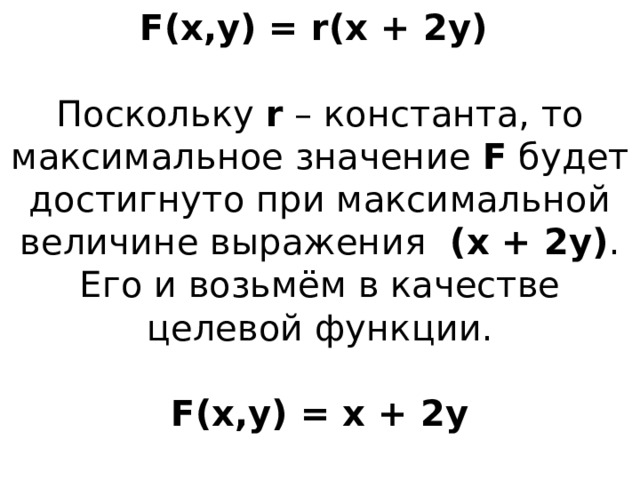
F(x,y) = r(x + 2y) Поскольку r – константа, то максимальное значение F будет достигнуто при максимальной величине выражения (x + 2y) . Его и возьмём в качестве целевой функции. F(x,y) = x + 2y

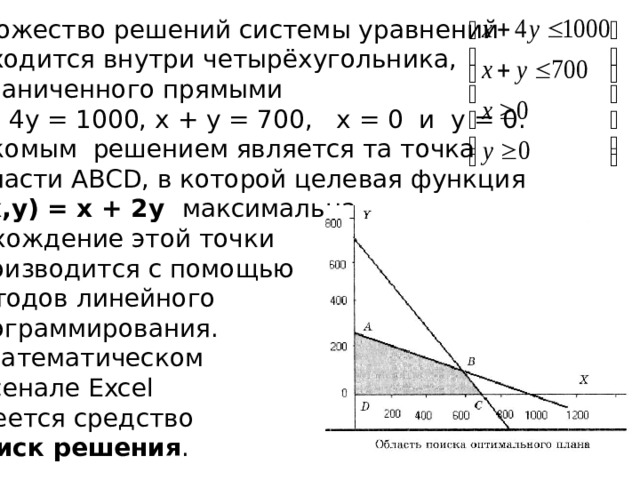
Множество решений системы уравнений

находится внутри четырёхугольника, ограниченного прямыми x + 4y = 1000, x + y = 700, x = 0 и y = 0.

Искомым решением является та точка области ABCD, в которой целевая функция

F(x,y) = x + 2y максимальна.

Нахождение этой точки

производится с помощью

методов линейного

программирования.

В математическом

арсенале Excel

имеется средство

Поиск решения .