ЗАДАЧИ ПО ТЕМЕ: «Площади фигур»
Площадь прямоугольника равна 75. Найдите стороны этого прямоугольника, если одна из них в 3 раза больше другой.
Найдите площадь прямоугольника, если одна из его сторон равна5, а угол между диагоналями равен 60°.
Площадь параллелограмма равна 90. Найдите высоту параллелограмма, проведенную к стороне, равной 12.
Найдите площадь равностороннего треугольника, сторона которого равна 12.
Вычислите площадь трапеции АВСД с основаниями АД и ВС, если АД=20, ВС=4, АВ=16 и угол А=30°.
Найдите площадь равнобедренной трапеции, основания которой равны 8 и 12, а боковая сторона равна 10.
Площадь прямоугольника равна 520 м2, а отношение его сторон равно 2: 5. Найдите периметр данного прямоугольника.
Стороны параллелограмма равны 5 см и 11 см. Найдите его площадь, если один из углов равен 30°.
Найдите площадь ромба со стороной 24 см и углом 120°.
Найдите площадь параллелограмма, периметр которого равен 42 см, а высоты равны 8 см и 6 см.
Найдите периметр ромба, площадь которого равна 48 см2 а острый угол равен 30°.
Найдите площадь равнобедренной трапеции, у которой основания равны 8 см и 18 см, а боковая сторона равна средней линии.
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Стороны треугольника относятся как З : 25 : 26. Его площадь равна 144 см2. Найдите периметр данного треугольника.
Основание равнобедренного треугольника равно 5 см. Медианы боковых сторон перпендикулярны. Найдите площадь данного треугольника.
В прямоугольном треугольнике сумма катетов равна m, а гипотенуза равна с. Найдите площадь треугольника, не вычисляя его катетов.
В четырехугольнике АВСD диагонали перпендикулярны и равны 4 см и 11 см. Найдите его площадь.
Точка касания круга, вписанного в прямоугольный треугольник, делит гипотенузу на части, равные 4 см и 6 см. Найдите площадь этого круга.
Решение задач
1 .Дано: прямоугольник ABCD, B C
.Дано: прямоугольник ABCD, B C
AB BC в 3раза
S=75см2
Найти: все стороны A D
Решение:
Пусть AB=x, тогда BC=3x
S=3x* x=3x2
3x2=75
x2=25 x=5
О

 твет: AB=5см, BC=15см B C
твет: AB=5см, BC=15см B C
2. Дано: прямоугольник ABCD,
AB=5, BOA=60°
Найти: SABCD A D
Решение:
1)∆BOA-равносторонний, т.к. ВО=АО, как половины диагоналей прямоугольника,
BOA=60° , значит BOA=AOB=60°.
BO=AO=AB=5см
2)Рассмотрим ∆ABD, он прямоугольный,
BD=10, AB=5, по т.Пифагора:
BD2=AB2+AD2, AD2=100-25=75, AD=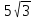
3) SABCD =AB*AD=5*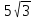 =25
=25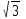
Ответ: SABCD=25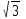
3
 .Дано: параллелограмм ABCD, B C
.Дано: параллелограмм ABCD, B C
AD=12, SABCD=90cм2
Найти: высоту BH
Решение: A D
S=BH*AD H
90=BH*12 BH=7,5
Ответ: BH=7,5см
4.Дано: равносторонний ∆,
где одна из сторон равна 12
Найти: S
Решение:
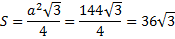
Ответ:S=36 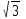 см2
см2
5
 .Дано: трапеция ABCD, B C
.Дано: трапеция ABCD, B C
AB=16, AD=20, BC=4, BAD=З0°
Найти: SABCD
Решение: A H D

BH=8(т.к.катет, лежащий против угла в З0°)
SABCD=12*8=96
Ответ: SABCD=96см2
6.Дано: равнобедренная трапеция ABCD(Cм.рис.к задаче№5)
AB=CD=10см, ВС=8см, AD=12см
Найти: SABCD
Решение:
1)По т.Пифагора в ∆ABH:
AB2=AH2+BH2
100=4+ BH2
BH2=96 BH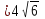
2)SABCD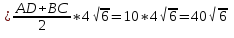
Ответ: SABCD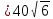 см2
см2
7.Дано: прямоугольник ABCD, SABCD=520м2, AB:BC=2:5
Найти: PABCD
Р ешение: B C
ешение: B C
1)Пусть x-одна часть, тогда AB=2x, BC=5x, P=2(AB+BC),
14x=P
2)2x*5x=S, 2x*5x=520 A D
10x2=520
x2=52 x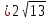
3)P=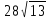
Ответ: P=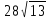 см
см
8.Дано: параллелограмм ABCD,
AB=5, BC=11, угол BAD=З0°
Ответ: SABCD
Решение:
SABCD=ab* =5*11*
=5*11*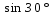 =55*
=55* =27,5
=27,5
Ответ: SABCD=27,5см2
9.Дано: ромб ABCD, B
A B=AD=24, =120°
B=AD=24, =120°
Найти: SABCD
Р ешение: A C
ешение: A C
DAH=
1)Ромб-параллелограмм H
2)по т.Пифагора: D
AH2=AD2+DH2
AH2=576-144=432
AH
3)SABCD AH*DC
AH*DC
Ответ: SABCD см2
см2
10.Дано: параллелограмм ABCD,
Найти: SABCD
Р

 ешение: B C
ешение: B C
AB+AD=21см, т.к. P=42см H
1)SABCD=BH1*AD SABCD=BH*CD
SABCD=6*AD SABCD=8*CD A D
6 AD=8*CD H1
2)Пусть AD=x, CD=21-x
6x=8(21-x)
6x=168-8x
14x=168 x=12
AD=12
3)SABCD=6*12=72
Ответ: SABCD=72см2
11.Дано: ромб ABCD,
S ABCD=48cм2, ABC=
ABCD=48cм2, ABC= B
B
Н айти: PABCD H
айти: PABCD H
Решение:
1)Ромб-параллелограмм A C
2)Sр=HC*AB=48
HC=x, AB=2x
x*2x=48 D
2x2=48
x2=24 x= =
=
3)P=4x=
Ответ: PABCD= см
см
12.Дано: равнобедренная трапеция ABCD,
BC=8см, AD=18см,
F

 H-средняя линия, AB=CD=FH B C
H-средняя линия, AB=CD=FH B C
Н айти: SABCD F H
айти: SABCD F H
Решение:
1)AH1=5, H2D=5 A H1 H2 D
FH=(18+8):2=13
2)По т.Пифагора:

169=25+
 =144
=144 
3)SABCD
Ответ: SABCD=156см2
13.Дано: прямоугольная трапеция ABCD,
большая боковая сторона равна сумме оснований,
CH=12см
Найти:S прямоугольника, стороны которого равны основаниям трапеции
Решение:
1
 )BC=AH=x, HD=y, CD=2x+y B C
)BC=AH=x, HD=y, CD=2x+y B C
S=x(x+y)=x2+x
2)Из ∆CHD по т.Пифагора:
С D2=CH2+HD2
D2=CH2+HD2
(2x+y)2=144+y2 A H D
4x2+4xy+y2=144+ y2
x2+xy=36=S
Ответ: S=36см2
14.Дано: ∆ABC,
AB:BC:AC=З:25:26
S
 ABC=144см2 B
ABC=144см2 B
Найти: PABC
Р ешение:
ешение:
1)По формуле Герона: A C
p
S


2)36x2=144
x2=4 x=2
AB=6, BC=50, AC=52
3)PABC=108cм
Ответ: PABC=108cм
1
 5.Дано: ∆ABC-равнобедренный, B
5.Дано: ∆ABC-равнобедренный, B
АС –основание, АС=5см,
м
 едианы боковых сторон перпендикулярны C1 A1
едианы боковых сторон перпендикулярны C1 A1
Найти: S∆
Решение: A H C
1)Рассмотрим ∆AA1C и ∆CC1A.У них:
AC-общая, C1A=A1C(как половины раных сторон),
уголA=уголC(т.к.углы при основании равнобедренного ∆-ка)
=∆AA1C=∆CC1A(по углу и двум сторонам)
AA1=CC1,т.к.медианы в ∆-ке при пересечении делятся пополам
в отношении 2:1,считая от вершины,то CO=AO
∆COA-равнобедренный
2)Пусть CO=AO=x
25=x2+ x2
25=2x2
x2= x=
x=
3)OH 
OH 
4)S∆
Ответ: S∆=18,75см2
16.Дано: прямоугольный ∆
с умма катетов равна m,
умма катетов равна m,
гипотенуза равна с
Найти: S∆, не вычисляя его катетов a c
Решение:
a + b=m
S= b
b
1)По т.Пифагора:
a2+b2=c2
(a+b)2=m2
a2+2ab+ b2=m2
2ab+c=m2
2ab=m2-c ab=
2) S∆=
Ответ: S∆=
17.Дано: четырехугольник ABCD,
A
 C, BD-диагонали, AC BD, AC=4см, BD=11см
C, BD-диагонали, AC BD, AC=4см, BD=11см
Найти: SABCD
Решение:
S
 =S1+S2,где S1=SABC, S2=SADC B
=S1+S2,где S1=SABC, S2=SADC B
S1
S
 2 A C
2 A C
 =
=
S=  +
+ =
= (
( )=
)= =22 D
=22 D
Ответ: SABCD=22см2
18.Дано: ∆ABC-прямоугольный,
т очка касания круга, вписанного в ∆ABC, B
очка касания круга, вписанного в ∆ABC, B
делит гипотенузу на части, равные 4 см и 6 см
Н айти: Sкруга O
айти: Sкруга O
Р
 ешение: M R
ешение: M R
1)Отрезки касательных, проведенных из одной точки
к одной окружности равны. C N A
4=AO=AN, 6*OB=MB, MC=CN=x
AB=10, AC=4+x, BC=6+x
2)По т.Пифагора:
(4+x)2+(6+x)2=100
16+8x+x2+36+12x+x2=100
2x2+20x-48=0
x2+10x-24=0
x1=-12(не удовлетв. усл.) x2=2
R=2
3) Sкруга= 2=4
2=4
Ответ: Sкруга= 4
Sкруга= 4







 .Дано: прямоугольник ABCD, B C
.Дано: прямоугольник ABCD, B C

 твет: AB=5см, BC=15см B C
твет: AB=5см, BC=15см B C
 .Дано: параллелограмм ABCD, B C
.Дано: параллелограмм ABCD, B C
 .Дано: трапеция ABCD, B C
.Дано: трапеция ABCD, B C ешение: B C
ешение: B C


















