| Геометрия – наука, занимающаяся изучением геометрических фигур (точка, прямая, отрезок, луч, угол, треугольник, прямоугольник и др). |
| 
ПЛАНИМЕТРИЯ Рассматриваются свойства фигур на плоскости. Например, отрезков, треугольников, прямоугольников и др. |
СТЕРЕОМЕТРИЯ Рассматриваются свойства фигур в пространстве. Например, параллелепипедов, цилиндров, пирамид и др. |
| Понятие | Определение понятия, его сущность, обозначения, примечания, чертежи |
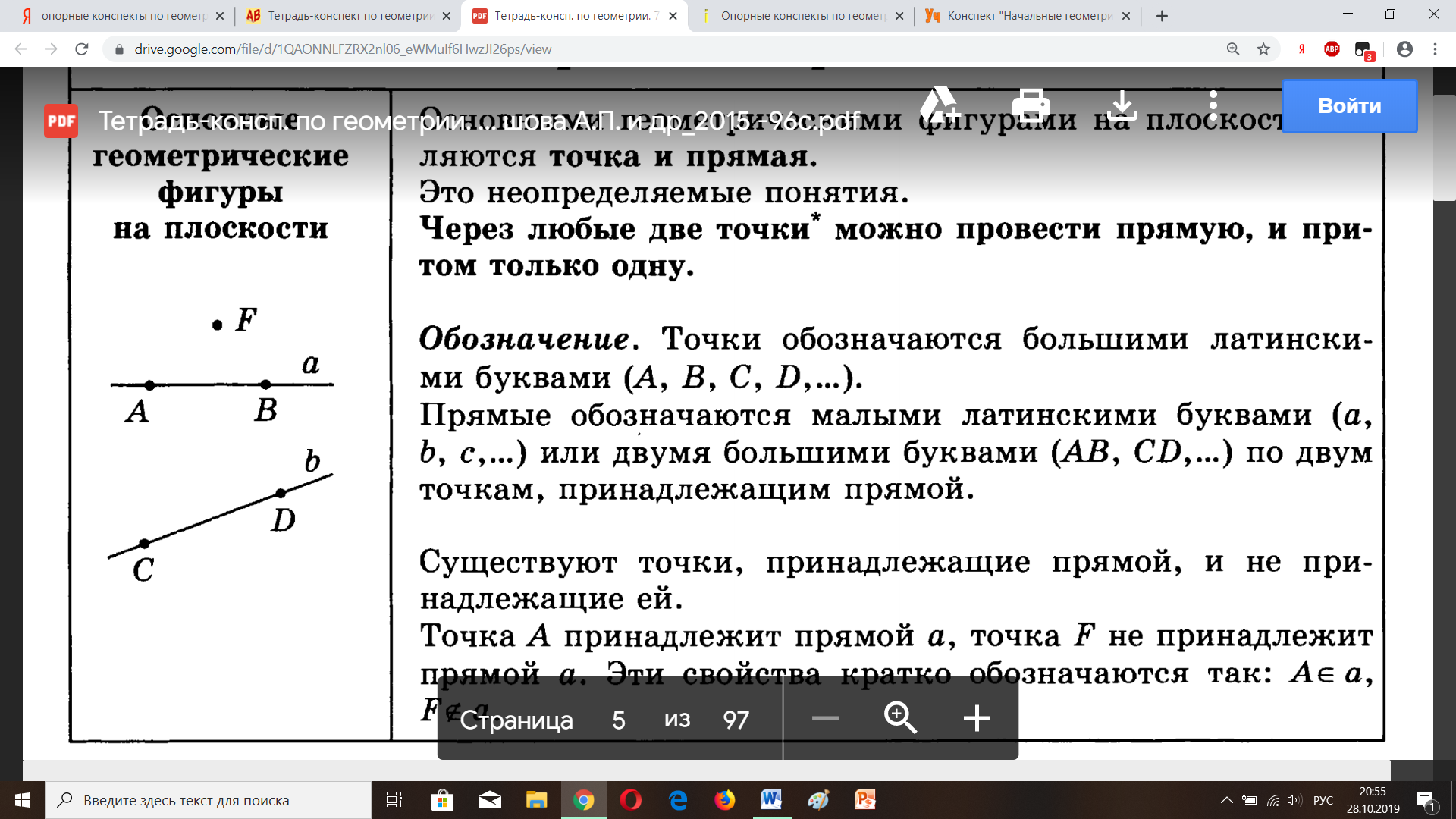
| Точка | Точки обозначаются БОЛЬШИМИ латинскими буквами (A, B, C, D, …) Прямые обозначаются МАЛЫМИ латинскими буквами (a, b, c, d, …) или двумя большими (АВ, СD, MK, …)
| 
|
Точки могут как принадлежать  прямой, так и не принадлежать ∉ ей. прямой, так и не принадлежать ∉ ей.
А  а; В а; В  а; С а; С b; D b; D  b; F ∉ а. b; F ∉ а. |
| Через любые две точки можно провести прямую, и при том только одну. | Прямая не имеет ни начала, ни конца. Она бесконечна. | 
| Две прямые либо имеют только одну общую точку, либо не имеют общих точек. |
|
| Прямая |
| Отрезок | Отрезок – часть прямой, ограниченная двумя точками (концами отрезка). Отрезок имеет начало и конец. | 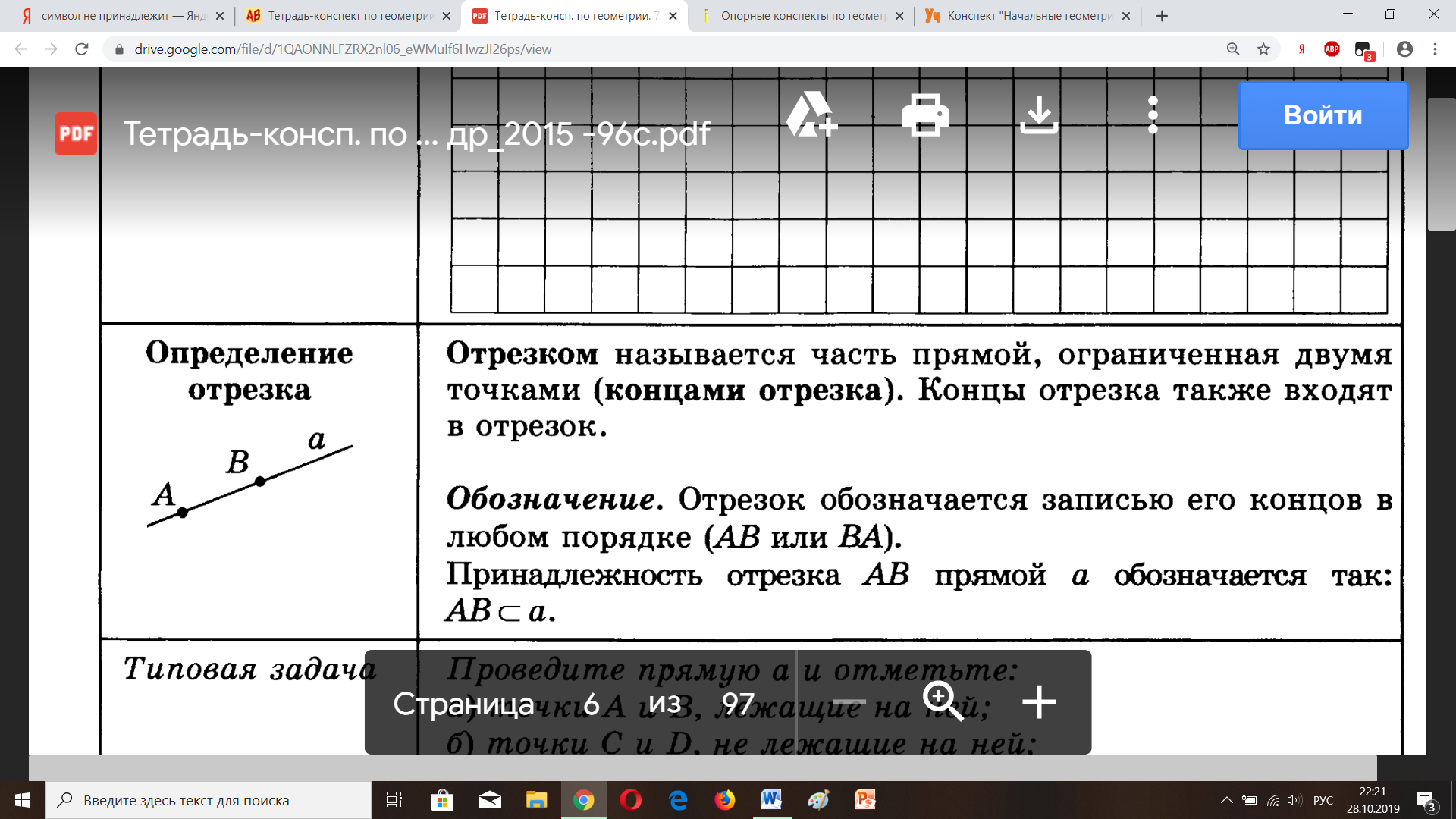
| Обозначение: отрезок АВ или отрезок ВА Концы отрезка: А, В |
| | 
| Два отрезка равны, если эти отрезки полностью совмещаются наложением. Если отрезки наложением не совмещаются, то меньшим считается тот, который составляет часть другого. АС АВ; СВ АВ | |

|
Точка отрезка, делящая его пополам, т. е. на два равных отрезка, называется серединой отрезка. АС = СВ, С – середина отрезка | - Равные отрезки имеют равные длины. - Меньший отрезок имеет меньшую длину. - Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих отрезков. АВ = АС + СВ |
| Луч | | 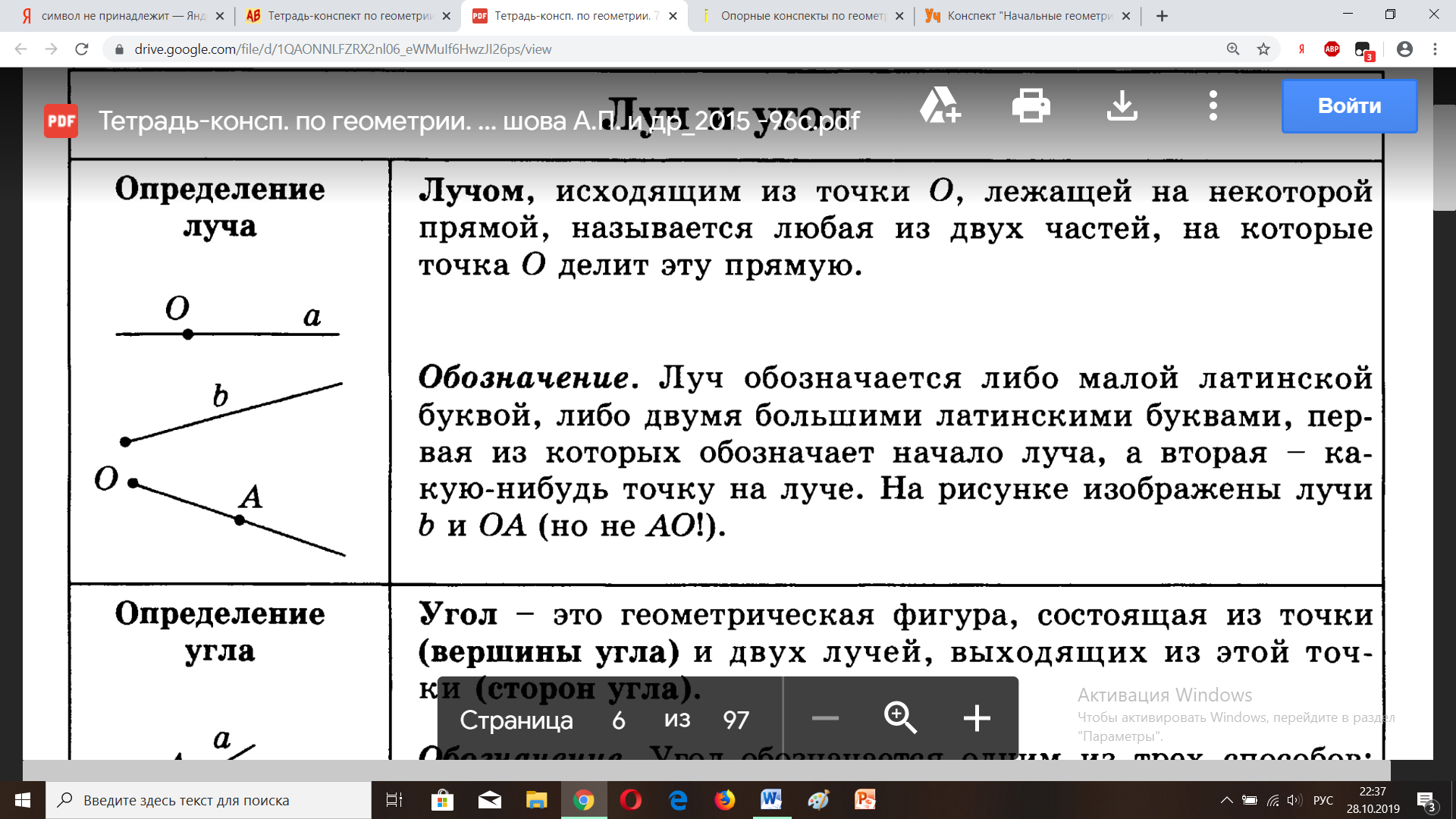
| Лучом, исходящим из точки О, лежащей на некоторой прямой, называется любая из двух частей, на которые точка О делит эту прямую. Луч имеет начало, но не имеет конца. Обозначение: b, OA |
|
| Угол | | 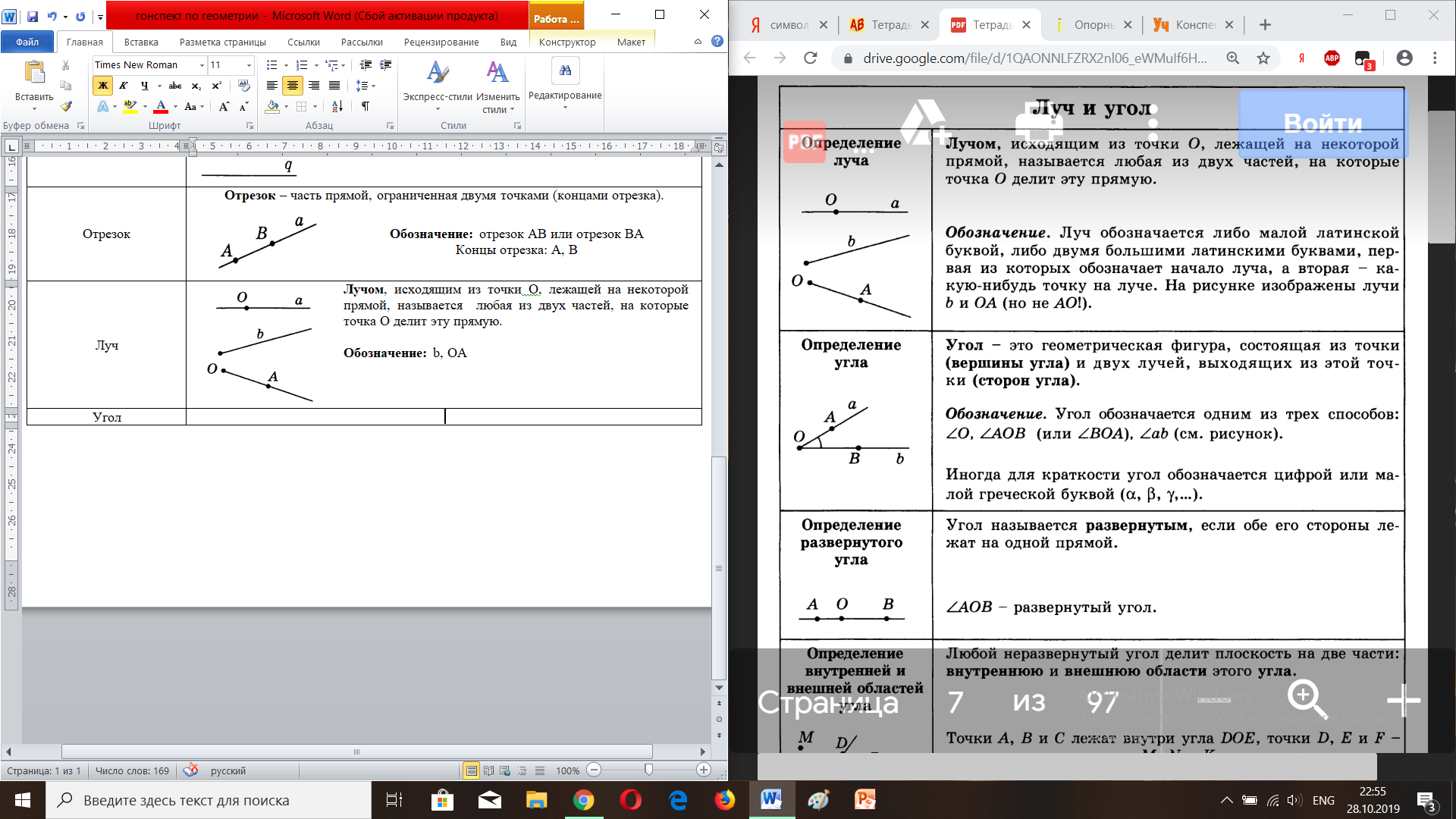
| Угол – это геометрическая фигура, состоящая из точки (вершины угла) и двух лучей, выходящих из этой точки (сторон угла). Обозначение: ∠АОВ, ∠ab, ∠О, ∠ВОА | | 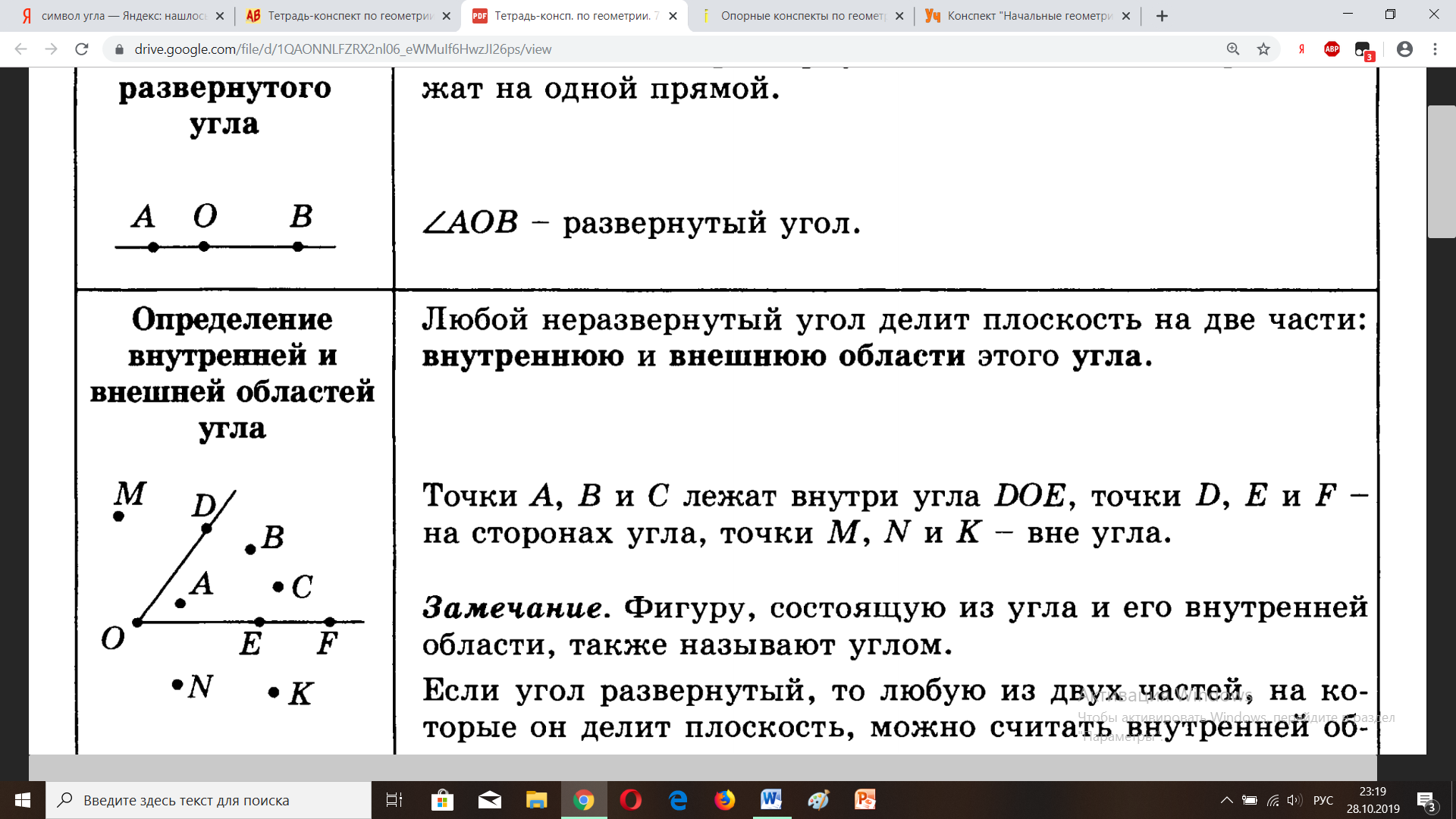
| Любой неразвернутый угол делит плоскость на две части: внутреннюю и внешнюю области этого угла.
Точки А, В, С лежат внутри ∠DOE, точки D, E, F – на сторонах угла, точки M, N, K - вне угла. | | 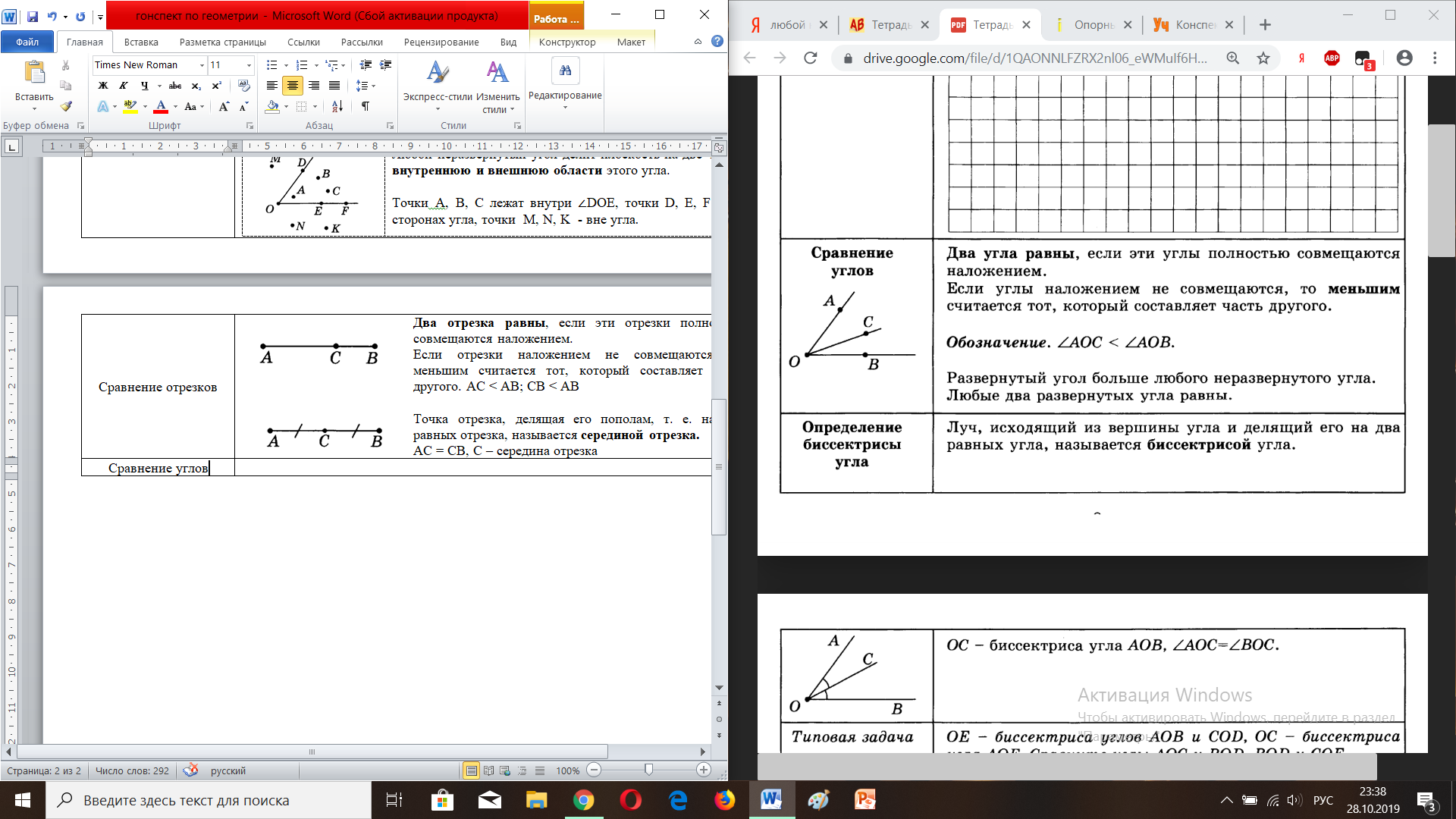
| Два угла равны, если эти углы полностью совмещаются наложением. Если углы наложением не совмещаются, то меньшим считается тот, который составляет часть другого. ∠АОС ∠АОВ; ∠ВОС ∠АОВ Развернутый угол больше любого неразвернутого угла. Любые два развернутых угла равны. |
| | 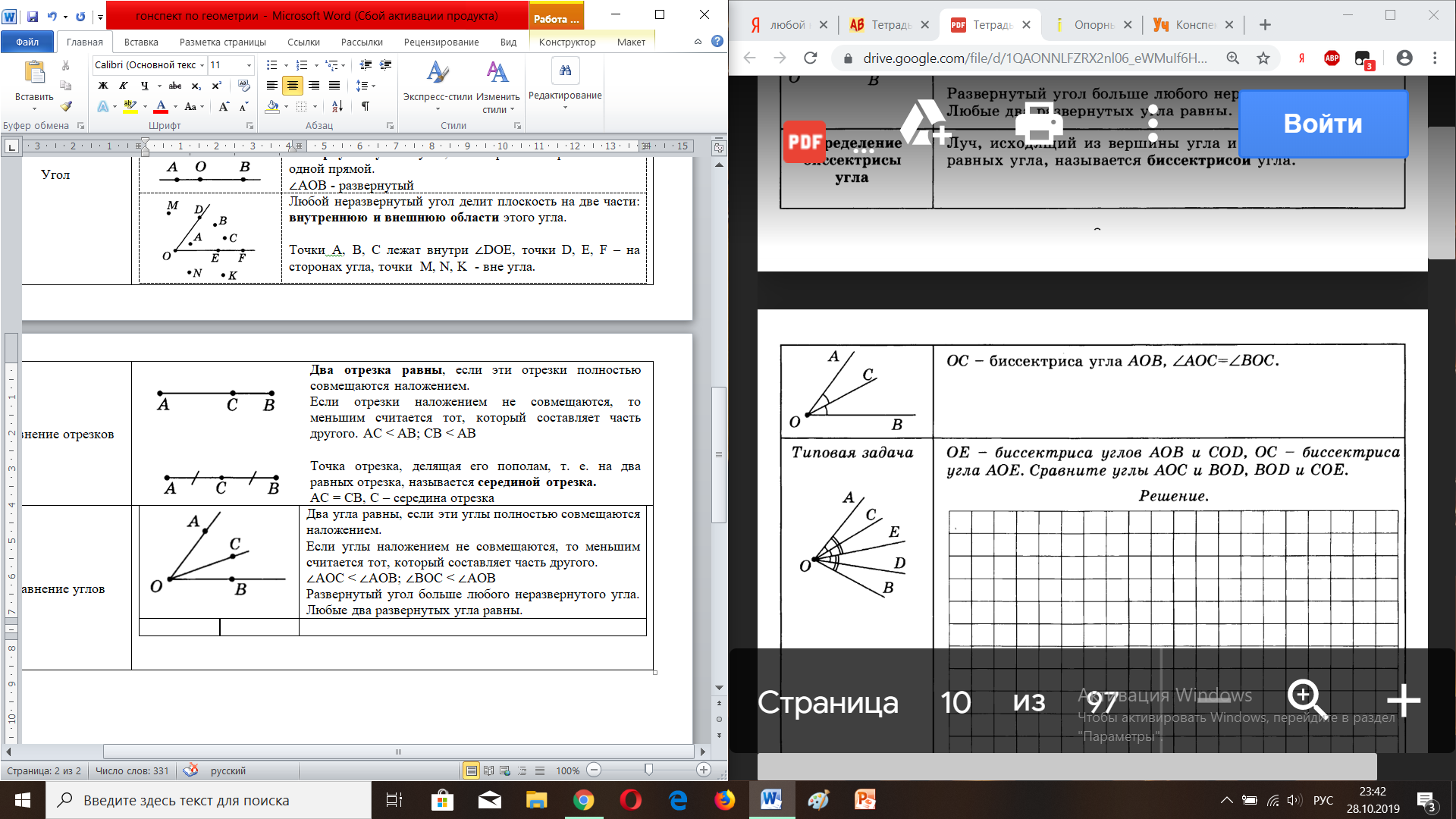
| Луч, исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла. ОС – биссектриса ∠АОВ ∠АОС = ∠ВОС |
| - Равные углы имеют равные градусные меры. - Меньший угол имеет меньшую градусную меру. - Если луч делит угол на два угла, то градусная мера всего угла равна сумме градусных мер этих углов. ∠АОВ = ∠АОС + ∠СОВ - Развернутый угол равен 180◦ |  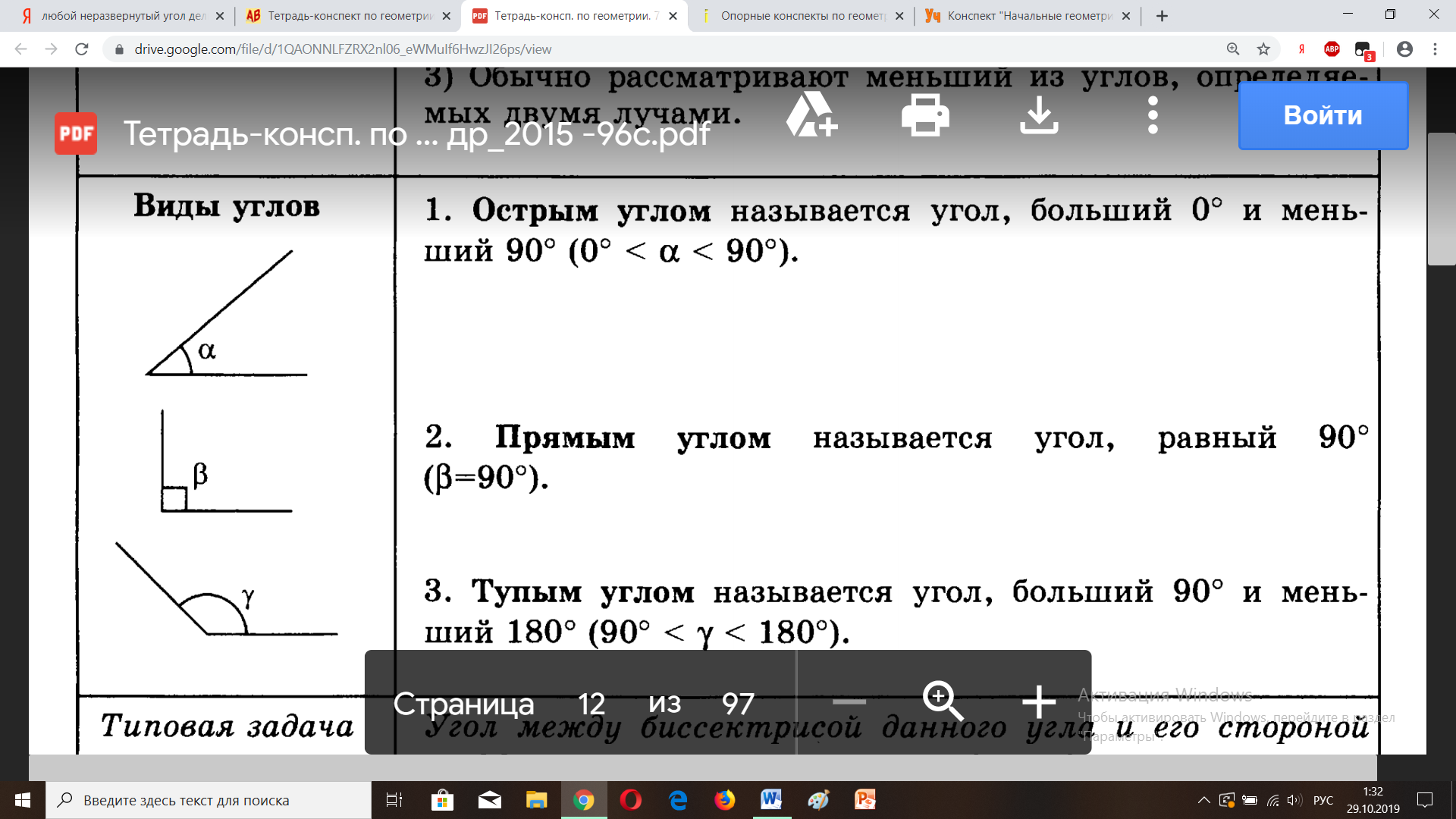
|
Развернутый угол – равен 180◦
Острый угол – угол больший 0◦ , но меньший 90◦
Прямой угол – угол, равный 90◦
Тупой угол – угол больший 90◦, но меньший 180◦ |
|
| Перпендикулярные прямые | | 
| Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
ДВЕ ПРЯМЫЕ, ПЕРПЕНДИКУЛЯРНЫЕ К ТРЕТЬЕЙ ПРЯМОЙ НЕ ПЕРЕСЕКАЮТСЯ |
|








 прямой, так и не принадлежать ∉ ей.
прямой, так и не принадлежать ∉ ей.



















