Нахождение наибольшего, наименьшего значения функции.
Наибольшее и наименьшее значение непрерывной функции f(x) на отрезке [a; b] достигаются в критических и стационарных точках, то есть в точках, в которых производная функции равна нулю f′(x)=0 или не существует, либо на концах отрезка [a; b].
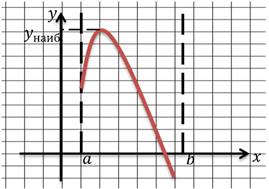
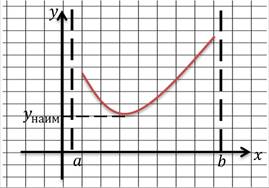
Теорема. Пусть функция y = f(x) непрерывна на промежутке X и имеет внутри него единственную стационарную или критическую точку x0. Тогда:
а) если x0 − точка максимума, то yнаиб = f(x0)
б) если x0 − точка минимума, то yнаим = f(x0)
Давайте геометрически проиллюстрируем эту теорему
Алгоритм
нахождения наибольшего (наименьшего) значения функции на отрезке[a; b]
1) Найти производную функции f '(x)
2) Найти критические (стационарные) точки f '(x) = 0
3) Отобрать из них те, что лежат внутри отрезка [а;b ]
4) Найти значения функции в этих точках и на концах отрезка.
5) Выбрать наибольшее и наименьшее из них и записать ответ
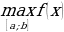
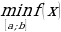
Пример:
Найти наибольшее и наименьшее значение функции f(x) = x3 – 1,5 x2 – 6x + 1
на отрезке [– 2; 0].
1) f '(x) = 3x2 – 3x – 6
2) 3x2 – 3x – 6 = 0
x2 – x – 2 = 0
D = 9
x1 = 2
x2 = – 1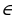 [– 2; 0]
[– 2; 0]
4) f(–1) = (–1)3 – 1,5∙ (–1)2 – 6 ∙(–1) + 1 = 4,5
f(–2) = (–2)3 – 1,5∙ (–2)2 – 6 ∙(–2) + 1= –1
f(0) = 03 – 1,5 ∙ 02 – 6 ∙ 0 + 1= 1
5) 
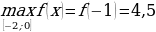
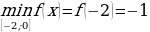
Решить самостоятельно:
1. Найти наименьшее значение функции f(x) = х2 – 4х на промежутке [1;3]
2. Найти наибольшее значение функции f(x) = х3 + 6х2 + 9х + 3 на промежутке [– 4; – 2]
3. Найти наименьшее значение функции f(x) = 1 + cos х на промежутке [ 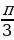 ;
; 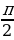 ]
]









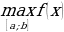
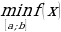
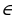 [– 2; 0]
[– 2; 0]
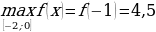
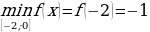
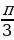 ;
; 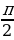 ]
]



















