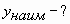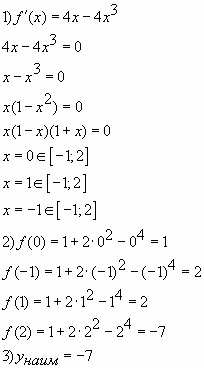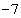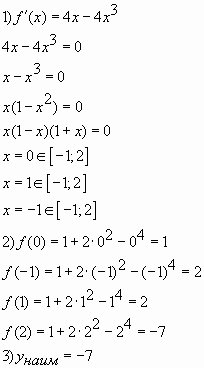Нахождение наибольшего и наименьшего значений функции без производной
Дано: 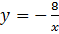 ,
, 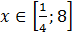 . Нарисуем график функции (см. рис.1).
. Нарисуем график функции (см. рис.1).
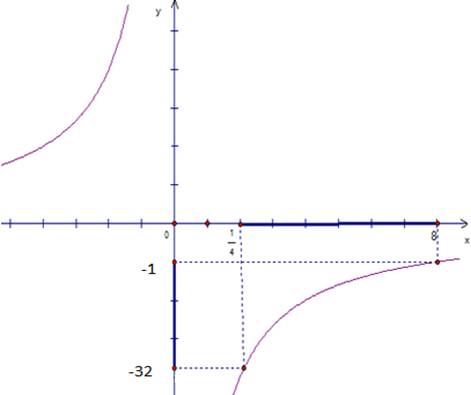
Рис. 1. График функции 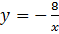 .
.
Известно, что эта функция возрастает на промежутке 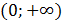 , значит, она возрастает и на отрезке
, значит, она возрастает и на отрезке 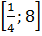 . А значит, если найти значение функции в точках
. А значит, если найти значение функции в точках 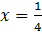 и
и 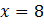 , то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.
, то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.

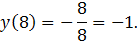
Когда аргумент возрастает от  до 8, функция возрастает от
до 8, функция возрастает от 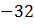 до
до 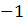 .
.
Ответ: 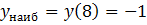 ;
;  .
.
4. Нахождение наибольшего и наименьшего значений функции с помощью производной
(а)
Дано:  ,
, 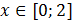 . Найти наибольшее и наименьшее значение функции на данном отрезке.
. Найти наибольшее и наименьшее значение функции на данном отрезке.
Если в предыдущем случае можно было обойтись без производной – мы знали, как себя ведет функция, то в данном случае функция довольно сложная. Поэтому, ту методику, которую мы упомянули на предыдущей задаче, применим в полном объеме.
-
Найдем производную 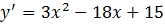 . Найдем критические точки
. Найдем критические точки  , отсюда
, отсюда 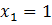 ,
,  - критические точки. Из них выбираем те, которые принадлежат данному отрезку:
- критические точки. Из них выбираем те, которые принадлежат данному отрезку: 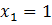 . Сравним значение функции в точках
. Сравним значение функции в точках
 ,
, 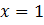 ,
,  . Для этого найдем
. Для этого найдем
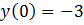 ;
;
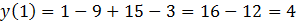 ;
;
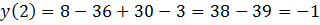 .
.
Проиллюстрируем результат на рисунке (см. рис.3).
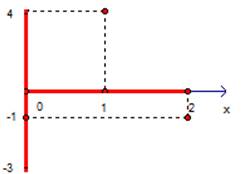
Рис. 3. Пределы изменения значений функции 
Видим, что если аргумент меняется от 0 до 2, функция изменяется в пределах от -3 до 4. Функция меняется не монотонно: она либо возрастает, либо убывает.
Ответ:  ;
;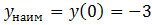 .
.
Алгоритм решения задачи на нахождение наибольшего и наименьшего значений функции
Итак, на трех примерах была продемонстрирована общая методика нахождения наибольшего и наименьшего значения функции на промежутке, в данном случае – на отрезке.
Алгоритм решения задачи на нахождение наибольшего и наименьшего значений функции:
1. Найти производную функции.
2. Найти критические точки функции и отобрать те точки, которые находятся на заданном отрезке.
3. Найти значения функции на концах отрезка и в отобранных точках.
4. Сравнить эти значения, и выбрать наибольшее и наименьшее.
6. Решение задачи
Рассмотрим еще один пример.
Найти наибольшее и наименьшее значение функции  ,
, 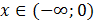 .
.
Ранее был рассмотрен график этой функции (см. рис.4).
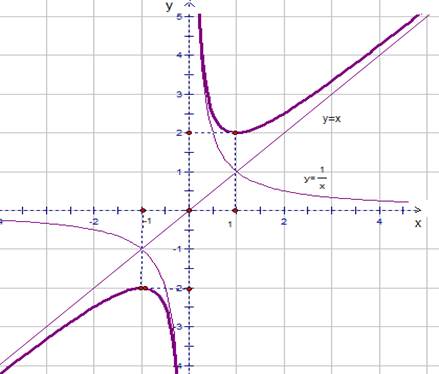
Рис. 4. График функции  .
.
На промежутке 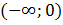 область значения этой функции
область значения этой функции 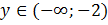 . Точка
. Точка  - точка максимума. При
- точка максимума. При 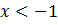 - функция возрастает, при
- функция возрастает, при 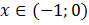 – функция убывает. Из чертежа видно, что
– функция убывает. Из чертежа видно, что 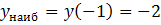 ,
, 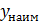 - не существует.
- не существует.
7. Итог урока
Итак, на уроке рассмотрели задачу о наибольшем и наименьшем значении функции, когда заданным промежутком является отрезок; сформулировали алгоритм решения подобных задач.
Пример № 1. Найти наименьшее значение функции 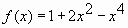 на отрезке
на отрезке 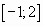 . (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).
. (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).
Решение:
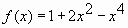
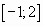
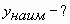
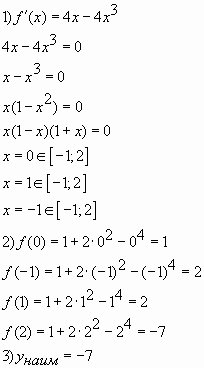
Ответ: 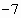
Пример






 ,
,  . Нарисуем график функции (см. рис.1).
. Нарисуем график функции (см. рис.1).
 , значит, она возрастает и на отрезке
, значит, она возрастает и на отрезке  . А значит, если найти значение функции в точках
. А значит, если найти значение функции в точках  и
и  , то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.
, то будут известны пределы изменения данной функции, ее самое большое и самое маленькое значение.

 до 8, функция возрастает от
до 8, функция возрастает от  до
до  .
. ;
;  .
. ,
,  . Найти наибольшее и наименьшее значение функции на данном отрезке.
. Найти наибольшее и наименьшее значение функции на данном отрезке. . Найдем критические точки
. Найдем критические точки  , отсюда
, отсюда  ,
,  - критические точки. Из них выбираем те, которые принадлежат данному отрезку:
- критические точки. Из них выбираем те, которые принадлежат данному отрезку:  ,
,  ,
,  . Для этого найдем
. Для этого найдем ;
; ;
; .
.
 ;
; .
. ,
,  .
.
 область значения этой функции
область значения этой функции  . Точка
. Точка  - точка максимума. При
- точка максимума. При  - функция возрастает, при
- функция возрастает, при  – функция убывает. Из чертежа видно, что
– функция убывает. Из чертежа видно, что  ,
,  - не существует.
- не существует.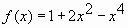 на отрезке
на отрезке 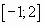 . (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).
. (Учитель совместно с учащимися записывает решение на доске последовательно проговаривая каждый пункт алгоритма).