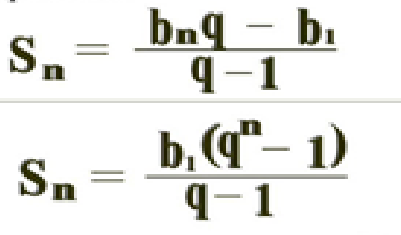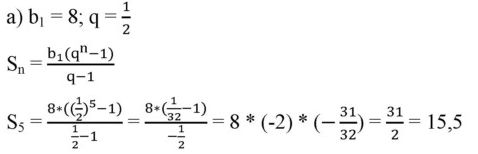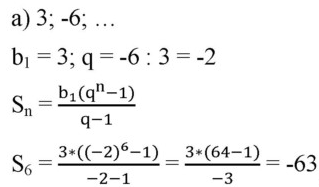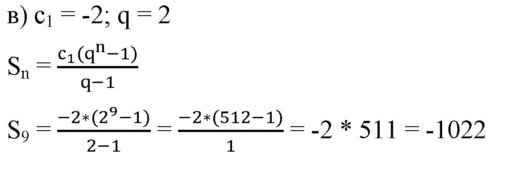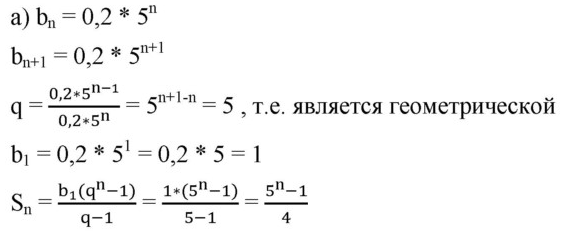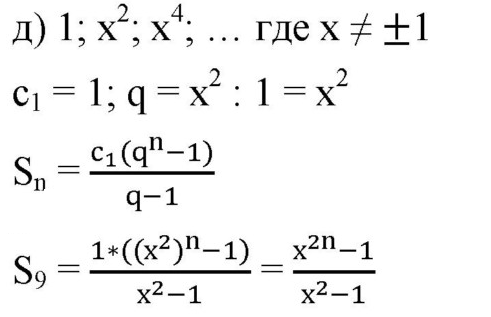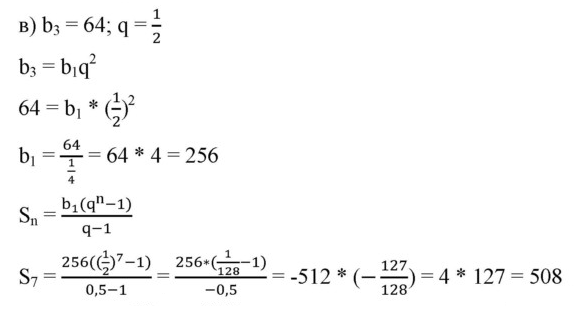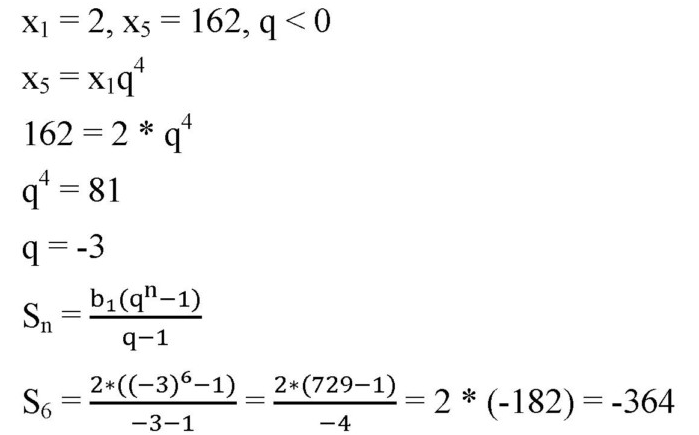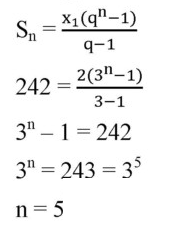Нахождение суммы первых n членов геометрической прогрессии

Урок № 90 9-Б,В,Ж 21,02,23 Шевель

Нахождение суммы первых n членов геометрической прогрессии

Цели: вывести формулу суммы первых п членов геометрической прогрессии; формировать умение применять эту формулу при решении задач.

Планируемые результаты: Предметные: познакомить учащихся с формулой суммы n-первых членов геометрической прогрессии. Выработать навыки применения формулы суммы п- первых членов геометрической прогрессии при решении заданий по данной теме. Личностные: готовность и способность к саморазвитию и самообучению, дисциплинированность, внимательность, трудолюбие и упорство в достижении поставленных целей, уважительное отношение к иному мнению. Метапредметные: самостоятельно создавать алгоритмы деятельности при решении проблем творческого и поискового характера, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий, уметь самостоятельно рефлексировать способы и условия действий, контролировать и оценивать процесс и результат деятельности; уметь слушать партнеров в процессе решения задач, оформлять решение в устной и письменной форме, уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; уметь осуществлять самоконтроль, саморегуляцию, ставить цель, оценивать результат собственной деятельности.

Тип урока: изучение нового материала.

Оборудование: доска, учебник, раздаточный материал, презентация , ПК

Математика есть единая симфония бесконечного.

Д. Гильберт

Давид Гильберт (23 января 1862 – 14 февраля 1943) – немецкий математик-универсал, внёс значительный вклад в развитие многих областей математики. В 1910 – 1920-е годы был признанным мировым лидером математиков. Его называют последним всесторонним математиком и самым замечательным учителем математиков 20 века.

Ход урока

I. ОРГАНИЗАЦИОННЫЙ МОМЕНТ.

Термин «прогрессия» имеет латинское происхождение. Термин «progression» был введен римским философом и математиком Боэцием (VI в.). Как вы думаете, что означает это слово?

 - «движение вперед», «успех»

 Не будем останавливаться и мы, а пойдем вперед в направлении изучения прогрессий.

Чтобы идти вперед, чаще оглядывайтесь назад, ибо вы забудете, откуда вы вышли и куда вам нужно идти. Давайте оглянемся, что на данный момент мы знаем о прогрессиях.

-Как называется прогрессия, которую мы изучаем?

Что мы о ней знаем, выясним в ходе устной работы

II. АКТУАЛИЗАЦИИ ЗНАНИЙ.

Тест на раздаточном материале

Задание 1

Найдите знаменатель геометрической прогрессии (b_n): 5, -2, ... .

1) -2,5

2) -7

3) 2,5

Задание 2

Каким не может быть третий член геометрической прогрессии, если первый член равен 2?

1) отрицательным 2) может быть любым числом 3) положительным

Задание 3

Каким может быть значение второго члена геометрической прогрессии, у которой b₁=3 и b₃=27?

1) -15 2) -9 3) 15 4) 9

Задание 4

Найдите первый член и знаменатель геометрической прогрессии, у которой c₂=30 и с₅=-30000.

1) c₁=-3, q=-10 2) c₁=3, q=-10 3) c₁=-3, q=10 4) c₁=3, q=10

Задание 5

Определите номер члена геометрической прогрессии равного 1024, если x₁=2 и q=2. В ответе укажите только число.

Задание 6

Найдите десятый член геометрической прогрессии, первый член которой равен 10 000 000, а знаменатель равен 0,1.

1) 10 2) 0,1 3) 1

4) 0,01

Задание 7

Найдите пропущенный член геометрической прогрессии: -1, ?, -9, 27, ... . В ответе укажите значение того члена, который обозначен знаком вопроса.

Задание 8

Найдите знаменатель геометрической прогрессии, первый член которой равен 12, а четвёртый член равен 96.

Задание 9

Среди последовательностей найдите те, которые являются геометрическими прогрессиями.

1) 3, 6, 9, ... 2) 6, -6, 6, -6, ... 3) 8, 4, 2, ... 4) 3, 9, 27, ...

Задание 10

Найдите шестой член геометрической прогрессии, первый член которой равен пяти а знаменатель q=-1.

1) 0 2) -1 3) -5 4) 5

1) 1;2) 1;3) 2; 4;4) 1;5) 10.; 6) 4;7) 3.; 8) 2.; 9) 2; 3; 4; 10) 3;

III. ИЗУЧЕНИЯ НОВОГО МАТЕРИАЛА И ЗАКРЕПЛЕНИЕ ЗНАНИЙ В СТАНДАРТНОЙ СИТУАЦИИ.

Мотивация: индийский принц вознаградить изобретателя шахмат. Пшеничные зерна 1, 2,4, 8,..в 2 раза больше S=2⁶⁴-1

ВИДЕОРОЛИК

Дано: 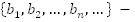геометрическая прогрессия.

Найти: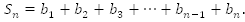

Решение: .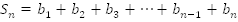

Умножим обе части этого равенства на q:

.

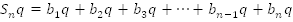И вычтем из первого равенства второе:

,

 ,

.

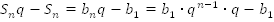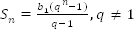В полученной формуле 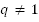, рассмотрим частный случай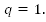

Геометрическая прогрессия 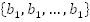 имеет nравных членов, поэтому ее сумма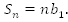

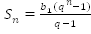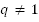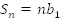Итак,  , при ;   при .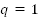

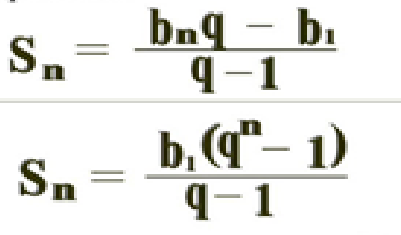
IV. МИНУТКА ОТДЫХА.

V. ЗАКРЕПЛЕНИЯ ЗНАНИЙ В НЕСТАНДАРТНОЙ СИТУАЦИИ.

№648(а = 15)

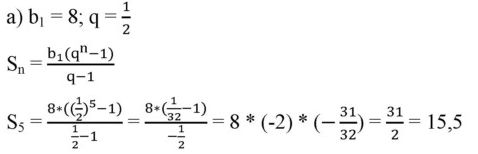
№649(а = -63)

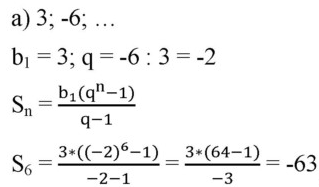
Самостоятельно № 650( в = -1022)

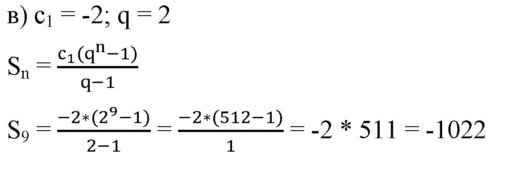
VI. ПРОВЕРКИ УСВОЕНИЯ ЗНАНИЙ

В парах № 651 (а)

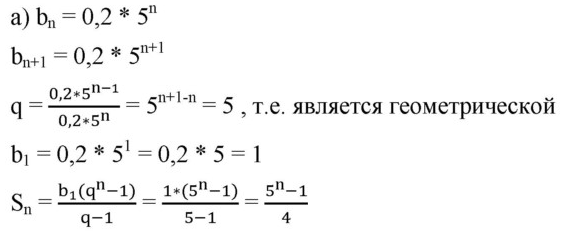
№652(д)

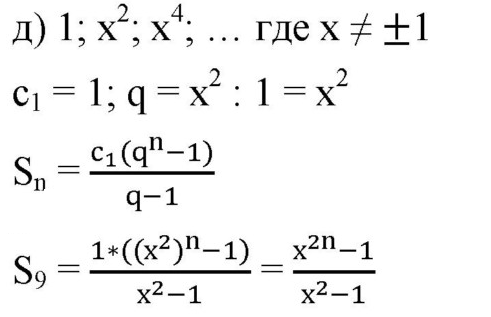
№653(в)

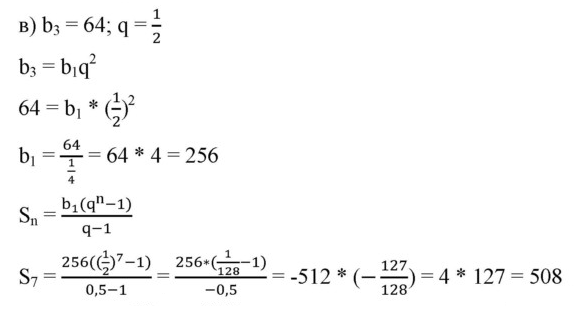
№655

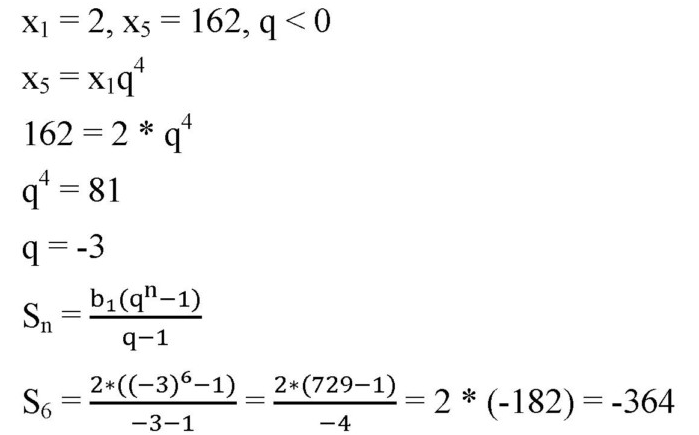
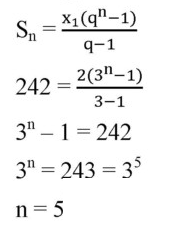
Резерв №657

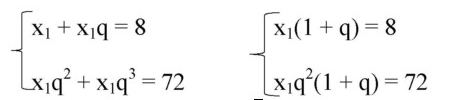
Поделив оба уравнения, 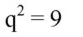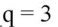, x₁=2

VII.  ОБЪЯСНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ

В заключение вспомним строки А. С. Пушкина из романа «Евгений Онегин», сказанные о его герое: «…не мог он ямба от хорея, как мы не бились, отличить». Отличие ямба от хорея состоит в различных расположениях ударных слогов стиха. Ямб – стихотворный метр с ударениями на четных слогах стиха (Мой дядя самых честных правил…), то есть ударными являются 2-й, 4-й, 6-й, 8-й и т. д. .Номера ударных слогов образуют арифметическую прогрессию с первым членом 2 и с разностью, равной двум: 2, 4, 6, 8, … Хорей – стихотворный размер с ударением на нечетных слогах стиха. (Буря мглою небо кроет…) Номера ударных слогов также образуют арифметическую прогрессию, но ее первый член равен единице, а разность по-прежнему равна двум: 1, 3, 5, 7, ….

Возрастающая прогрессия символизирует прогресс, движение вперед. Если же вернуться к истокам, то можно узнать, что первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания, как их решать.

 Для остальных домашнее задание: п. 28 выучить формулы № 648-651(б) ,652-653(г),656, по желанию №657

VIII ИТОГ УРОКА, выставление, комментирование оценок за работу на уроке.

Рефлексия.

Я запомнил, что… Я понял, что… Мне на уроке … Думаю, что …

А урок закончу словами Карла Гаусса: «Математика – царица наук, а арифметика – царица математики». Любите математику, учите математику, и тогда вам любая наука будет по плечу. Знайте: ничто не дисциплинирует человека, так, как математика, ничто не развивает его способности, так как математика, и  ничто не ведет вперед к успеху так, как математика.  Успеха и постоянного движения вперед! Урок закончен.

2