Содержание
ВВЕДЕНИЕ………………………………………………………………..……..3 ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ»...….5
Исторические сведения о нахождении высоты предмета с недоступной точкой………………………………………………………………………....5 Подобие треугольников. Признаки подобия треугольников……………..5
1.3 Задачи на определение высоты предмета…………………………………..8 ГЛАВА 2 ПРАКТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ»…………. …….18 2.1 Задача на нахождение расстояния………………………………………....18 2.2 Определение высоты новогодней ёлки с помощью зеркала……..………18 ЗАКЛЮЧЕНИЕ…………………………………………………………………23 Библиографический список…………………………………………………....24
ВВЕДЕНИЕ
Геометрию можно считать одной из самых древних наук. Наука в начале своего развития для человека несла практическую деятельность. Только лишь потом она сформировалась как самостоятельная наука, которая изучает геометрические фигуры. Геометрические знания активно применяются у людей в жизни, в науки, в быту, на производстве. Мы должны уметь рассчитать количество обоев в комнату, посчитать площадь квартиры и др. Кто-то с лёгкостью выполняет геометрические построения при изготовлении технических чертежей, или определяет расстояние до предмета. Геометрия всегда помогала решить те задачи, перед которыми её ставила жизнь[7].
Учение о подобии фигур на основе теории отношений и пропорций было создано в Древней Греции в 5-4 веках до нашей эры и существует и развивается до сих пор. Например, многие предметы, которые нам встречаются в быту среди детских игрушек подобны предметам из взрослого мира, тоже можно сказать и про одежду, обувь. Эти примеры можно продолжать и дальше. В конце концов, все люди подобны друг другу. Мы уже знаем, что в геометрии фигуры одинаковой формы принято называть подобными. В нашей работе по теме «Применение подобия треугольников при измерительных работах» мы рассмотрим, как свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности [4,8].
Геометрия помогает человеку идти по миру с широко открытыми глазами, учит внимательно смотреть вокруг и видеть красоту обычных вещей, смотреть и думать, думать и делать выводы.
Цель: Изучение применения подобия треугольников при измерительной работе на местности.
Задачи:
Анализ литературы по проблеме исследования.
Исторический обзор вопроса по проблеме исследования
Рассмотреть подобие треугольников, признаки подобия треугольников
Подобрать различные задачи на определение расстояния предмета
Научиться применять признаки подобия треугольников при решении геометрических задач на местности
Выполнить практическую работу по определению высоты предмета на местности
Гипотеза: если использовать различные способы определения высоты предмета, то эти результаты будут близки к фактическому размеру предмета.
ГЛАВА 1 ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ»
Исторические сведения о нахождении высоты предмета с недоступной точкой
Учение о подобии фигур было создано в Древней Греции в V – IV веке до н.э. трудами Гиппократа Хиосского, Архита Тарентского, Евдокса Книдского и других. Оно изложено в шестой книге «Начал» Евклида, начинающейся следующим определением: «Подобные прямолинейные фигуры суть те, которые имеют соответственно равные углы и пропорциональные стороны». Свойства подобных фигур издавна широко использовались на практике при составлении планов, карт. При выполнении архитектурных чертежей и чертежей различных деталей машин и механизмов. Жители Древнего Египта задались вопросом: «Как найти высоту одной из громадных пирамид?» Фалес нашёл решение этой задачи. Он воткнул длинную палку вертикально в землю и сказал: «Когда тень от этой палки будет той же длины, что и сама палка, тень от пирамиды будет иметь ту же длину, что и высота пирамиды»[3,7].
История практической геометрии тянулась от вавилонян и древних египтян. Некоторые черты развития практической геометрии можно отметить и в Древней Руси. Уже в XVI веке в России нужды землемерия, строительства и военного дела привели к созданию рукописных руководств геометрического содержания. Первое дошедшее до нас сочинение носит название "О земном верстании, как землю верстать". Оно является частью "Книги сошного письма", написанной в 1556 году при Иване IV. Сохранившаяся копия относится к 1629 году. При разборе Оружейной Палаты в Москве в 1775 году была обнаружена инструкция "Устав ратных, пушечных и других дел, касающихся до военной науки", изданная в 1607 и 1621 годах. Инструкция содержит некоторые геометрические сведения, которые сводятся к определенным приемам решения задач на нахождение расстояний [7].
Подобие треугольников. Признаки подобия треугольников
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника (рис 1)[1].
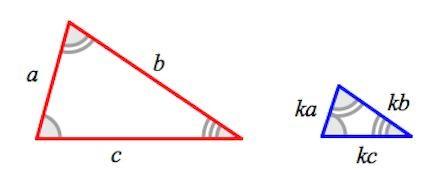
Рисунок 1- Подобные треугольники
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.
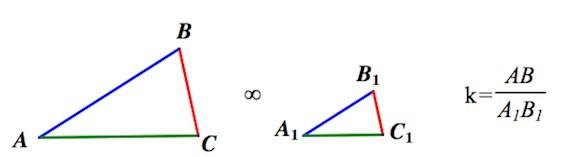 Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов (рис.2)[1].
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов (рис.2)[1].
Рисунок 2 – Демонстрируются сходственные стороны
Признаки подобия треугольников
Первый признак подобия треугольников: если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны (рис. 3)[1].
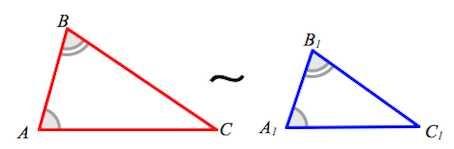
Рисунок 3 – Первый признак подобия треугольников
Если ∠B=∠B1 и ∠C=∠C1, то ΔABC∼ΔA1B1C1
Второй признак подобия треугольников: если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны (рис. 4)[1].
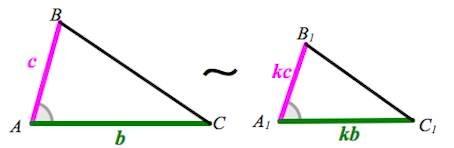
Рисунок 4 – Второй признак подобия треугольников
Если AB/A1B1=AC/A1C1 и ∠A=∠A1, то ΔABC∼ΔA1B1C1.
Третий признак подобия треугольников: если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны (рис. 5)[1].
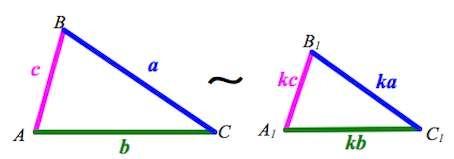
Рисунок 5 – Третий признак подобия треугольников
Если AB/A1B1=BC/B1C1=AC/A1C1, то ΔABC∼ΔA1B1C1.
Свойства подобных треугольников:
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Отношение периметров подобных треугольников равно коэффициенту подобия [7].

Рисунок 6 – Свойства подобных треугольников
Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
1.3. Задачи на определение высоты предмета
Задачи на нахождение расстояний всегда имели и имеют большое значение в военном деле. Многие задачи, требующие нахождения расстояния на местности решаются с помощью признаков подобия треугольников, но чаще всего применяется первый признак подобия треугольников по двум углам. Рассмотрим некоторые из них[2].
Задача на определение высоты предмета по длине его тени
Самый простой способ состоит в том, что в солнечный день можно пользоваться любой тенью, какой бы длины она ни была. Измерив свою тень или тень какого-нибудь шеста, вычисляют искомую высоту из пропорции
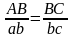 . (рис. 7)
. (рис. 7)
То есть высота дерева во столько раз больше вашей собственной высоты (или высоты шеста), во сколько раз тень дерева длиннее тени человека (или тени шеста)[3].
Это вытекает из геометрического подобия треугольников ABC и abc (по двум углам) (рис. 7).
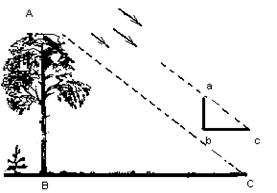
Рисунок 7 – Задача на определение высоты предмета по длине его тени
Этот способ называется способ Фалеса. В честь греческого мудреца Фалес Милетского, который научил египтян определять высоту пирамиды по длине ее тени еще за шесть веков до нашей эры.
Преимущества способа Фалеса заключается в том, что не требуются вычисления.
Недостатки заключаются в том, что измерить высоту предмета невозможно при отсутствии солнца и, как следствия, отсутствия тени.
Задача на определение высоты предмета с помощью прямоугольного треугольника
Для того, чтобы измерить высоту дерева BD, нужно приготовить равнобедренный прямоугольный ∆АВ1C1 (∠А=45°) и, держа его вертикально, отойти на такое расстояние, при котором, глядя вдоль гипотенузы АВ1, нужно увидеть верхушку дерева В (рис. 8)[3].
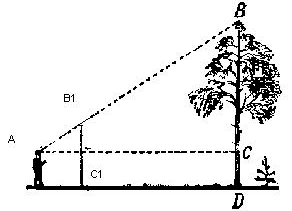
Рисунок 8 – Задача на определение высоты предмета с помощью прямоугольного треугольника
Так как ∠А общий для обоих треугольников, ∠АС1В1=∠АСВ=90о (по условию), тоАС1В1иАСВ– подобные (по признаку подобия о двух углах).
Тогда ∠АВ1C1=∠АВС=45о, =ВС=АС, но к получившейся длине мы должны еще прибавить рост человека, то есть длина дерева BD=ВС+СD.
Задача на определение высоты предмета с помощью булавочного прибора
Можно воспользоваться свойствами равнобедренного прямоугольного треугольника, обратившись к весьма простому прибору, который легко изготовить из дощечки и трех булавок. На дощечке любой формы намечают три точки – вершины равнобедренного прямоугольного треугольника – и в них втыкают по булавке (рис. 9)[7].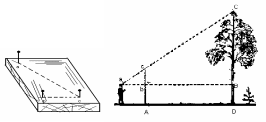
Рисунок 9 – Задача на определение высоты предмета с помощью булавочного прибора
Если нет под рукой чертежного треугольника для построения прямого угла, нет и циркуля для отложения равных сторон, то можно перегнуть любой кусок бумаги один раз, а затем поперек первого сгиба еще раз так, чтобы обе части первого сгиба совпали, - получим прямой угол. Та же бумага пригодится и вместо циркуля, чтобы отмерить равные расстояния. Отойдя от измеряемого дерева, нужно держать прибор так, чтобы один из катетов треугольника был направлен отвесно, для чего можно пользоваться ниточкой с грузиком, привязанным к верхней булавке. Приближаясь к дереву или удаляясь от него, всегда можно найти такое место А(рисунок 9), из которого, глядя на булавки, можно увидеть, что они покрывают верхушку С дерева: это значит, что продолжение гипотенузы ас проходит через точку С. Тогда, очевидно, расстояние аb=СВ, так как ∠а=45о. Следовательно, измерив расстояние аВ(или на ровном месте, одинаковое с ним расстояние АD)и прибавив BD,т.е. возвышение аА глаза над землей, получим искомую высоту дерева.
Задача на определение высоты предмета с помощью шеста
При отсутствии тени в пасмурную погоду можно воспользоваться способом измерения, который живописно представлен у Жюль Верна в известном романе «Таинственный остров» [3].
Необходимо воткнуть шест в землю. Место для шеста надо выбирать так, чтобы, лежа, как показано на рисунке 10, было видно верхушку дерева на одной прямой линии с верхней точкой шеста. Так как ABC– равнобедренный и прямоугольный, то ∠A=45о и, следовательно, АВ=ВС, т.е. искомой высоте 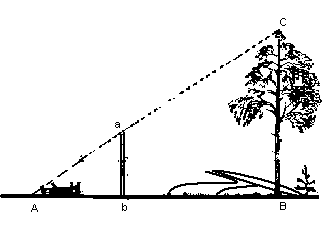 дерева.
дерева.
Рисунок 10 – Задача на определение высоты предмета с помощью шеста
Преимущества способа Жюль Верна: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить, высоту предмета не испачкавшись, так как приходится ложиться на землю [4].
Задача на определение высоты предмета с помощью записной книжки и карандаша
В качестве прибора для приблизительной оценки недоступной высоты можно использовать карманную записную книжку и карандаш. Она поможет построить в пространстве те два подобных треугольника, из которых получается искомая высота [7].
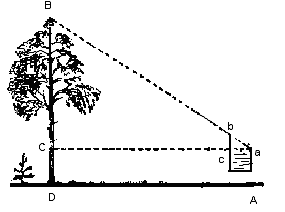
Рисунок 11 – Задача на определение высоты предмета с помощью записной книжки и карандаша
Книжку надо держать возле глаз так, как показано на упрощенном рисунке 11. Она должна находиться в отвесной плоскости, а карандаш выдвигаться над верхнем обрезом книжки настолько, чтобы, глядя из точки а видеть вершину В дерева покрытой кончиком b карандаша. Тогда вследствие подобия треугольников abc и аВС высота ВС определяется из пропорции
BC/bc=aC/ac [7].
Расстояние bc, ac и аС измеряются непосредственно. К полученной величине ВС надо прибавить еще длину CD,т.е. – на ровном месте – высоту глаза над почвой. Так как ширина ас книжки неизменна, то если всегда становиться на одном и том же расстоянии от измеряемого дерева, высота дерева будет зависеть только от выдвинутой части bc карандаша. Поэтому можно заранее вычислить, какая высота соответствует тому или иному выдвижению, и нанести эти числа на карандаш.
Задача на определение высоты предмета с помощью зеркала
На некотором расстоянии (рис. 12) от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркальце верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ЕD), во сколько раз расстояние ВС от зеркала до дерева больше расстояния СD от зеркала до наблюдателя [3].
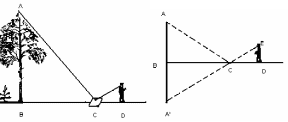
Рисунок 12 – Задача на определение высоты предмета с помощью зеркала
Способ основан на законе отражения света. Вершина А( рис. 13) отражается в точке А так что АВ=А’В. Из подобия же треугольников ВСА’ и CED следует, что A’B/ED=BC/CD.
В этой пропорции остается лишь заменить А’В равным ему АВ, чтобы обосновать указанное соотношение.
Преимущества способа: можно производить измерения в любую погоду; простота формулы. Недостатки: нельзя измерить, высоту предмета в густом насаждении, применяется к одиноко стоящему дереву [7].
Задача на определение высоты предмета с помощью высотомера лесника
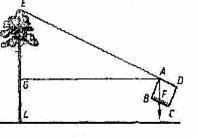 На рисунке 13 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10Х10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D.Наведя с помощью визиров сторону AD на вершину дерева Е и заметив деление шкалы, которое показывает отвес AF, лесник с помощью несложной формулы и находит высоту дерева [7].
На рисунке 13 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10Х10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D.Наведя с помощью визиров сторону AD на вершину дерева Е и заметив деление шкалы, которое показывает отвес AF, лесник с помощью несложной формулы и находит высоту дерева [7].
Рисунок 13 - Задача на определение высоты предмета с помощью высотомера лесника
Задача на нахождение высоты здания
Найдите высоту здания (в метрах), длина тени которого равна 27 м, если тень человека ростом 1 м 60 см равна 2 м 40 см [1,6].
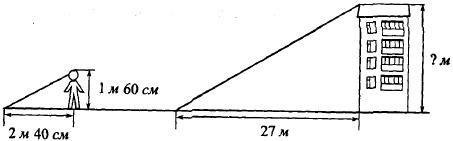
Рисунок 14 - Задача на нахождение высоты здания
Решение: Треугольники подобны (по двум углам), значит можно составить пропорцию:
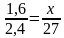 тогда,
тогда, 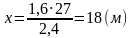
Задача на определение расстояния до недоступной точки
Для того, чтобы найти расстояние от пункта А до недоступного пункта В выбираем точку С, провешиваем отрезок АС и измеряем его. Затем измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник А1В1С1, у которого угол А1 равен углу А, угол С1 равен углу С, и измеряем длины сторон А1В1 и А1С1 этого треугольника. Так как треугольники АВС и А1В1С1 подобны, то из пропорциональности их сторон найдём АВ (рис. 15)[1].
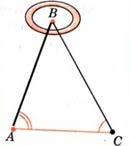 Рисунок 15 – Задача на определение расстояния до недоступной точки
Рисунок 15 – Задача на определение расстояния до недоступной точки
Задачи на нахождение расстояний
Задача «Неприятельская вышка». Открытый участок дороги находится на полосе АВ шириной в 50 м; неприятельский наблюдательный пункт находится на верху колокольни высотой MN=22 м. Какой высоты следует сделать вертикальную маску КВ на расстоянии 500 м от колокольни, чтобы закрыть дорогу от наблюдателя противника? (рис.16) [3]
Рисунок 16 – Задачи на нахождение расстояний
Дано:  AMN, АВ=50 м, MN=22м, BN=500 м.
AMN, АВ=50 м, MN=22м, BN=500 м.
Найти: КВ.
Решение: АКВ ~
АКВ ~  АМN (по двум углам
АМN (по двум углам  А – общий и
А – общий и  АВК и
АВК и  AMN – прямые, а если треугольники подобны, то все его элементы тоже подобны).
AMN – прямые, а если треугольники подобны, то все его элементы тоже подобны).
То есть , а 
Следовательно
Задачи на определение расстояния до кораблей в море
Первый способ. Пусть корабль находится в точке К, а наблюдатель в точке А. Требуется определить расстояния КА. Построив в точке А прямой угол, необходимо отложить на берегу два равных отрезка АВ=ВС. В точке вновь построить прямой угол, причем наблюдатель должен идти по перпендикуляру до тех пор, пока не дойдет до точки D, из которой корабль К и точка были бы видны лежащими на одной прямой. Прямоугольный треугольники ВСD и ВАК равны, следовательно, CD=AК, а отрезок CD можно непосредственно измерить [7].
Рисунок 17 – Задачи на определение расстояния до кораблей в море
Второй способ. Получил название - метод триангуляции, нашел применение в астрономии. С его помощью измерялись расстояния до небесных тел (рис. 18) [7].
Рисунок 18 – Метод триангуляции
Этот метод состоит из трех этапов:
Измерение углов 1 и 2 и расстояния АВ.
Построение  А'В'К' с углами 1 и 2 при вершинах А' и В' соответственно.
А'В'К' с углами 1 и 2 при вершинах А' и В' соответственно.
Учитывая подобие треугольников АВК, А'В'К' и равенство отрезков AB, А'К' и А'В' легко найти длину отрезка АК.
 .
.
ГЛАВА 2 ПРАКТИЧЕСКАЯ ЧАСТЬ ПО ТЕМЕ «ПРИМЕНЕНИЕ ПОДОБИЯ ТРЕУГОЛЬНИКОВ ПРИ ИЗМЕРИТЕЛЬНЫХ РАБОТАХ» 2.1 Задача на нахождение расстояния
Эксперимент проводился в парке на остановке Ручьёва в «Зимнем городке». Объектом измерения стала новогодняя ёлка (рис. 19).
Рисунок 19 – Ёлка в «Зимнем городке»
Измерим высоту дерева с помощью полученных знаний о подобных треугольниках.
Определим высоту дерева с помощью зеркала.
Для измерения дерева нам понадобились: зеркало, рулетка (рис. 20).
Рисунок 20 – Зеркало и рулетка
Мы положили зеркало, после чего начали отходить от него до тех пор, пока не увидели отражение в зеркале верхушки ёлки. Затем измерили расстояние от зеркала до дерева и расстояние от зеркала до человека. Заранее мы измерила рост человека, который участвует в эксперименте до глаз (рис. 21).
Рисунок 21 – Определяем высоту дерева при помощи зеркала
Дано: ВС=6,35 м расстояние от зеркала до дерева, ВС1=0,75 м расстояние от зеркала до человека, А1С1=1,425 м рост человека до глаз.
Найти: АС высота дерева.
Решение: Треугольники АСВ и А1С1В подобны по двум углам. Поэтому

Ответ: высота дерева 12,07 м, если мы его измерим с помощью зеркала.
Определим высоту дерева с помощью планшета
Для измерения дерева нам понадобится: планшет с изображением прямоугольного равнобедренного треугольника, нить с грузиком, рулетка. Катеты, изображенного в планшете прямоугольного равнобедренного треугольника, равны 10 см. Затем измерим расстояние от столба до человека рост которого мы заранее измерили (рис. 22).
С
 B D
B D
A E
Рисунок 22 – Чертёж определения высоты дерева при помощи планшета
Дано: BD=10,755 м расстояние от человека до дерева. DE=1,425 м рост человека до глаз.
Найти: AC высоту дерева.
Решение: Поскольку треугольник на планшете и треугольник BCD подобны, оба прямоугольные и равнобедренные, то BC=BD.
Следовательно, AC=BC+BA=BD+DE=10,755+1,425=12,18 (м).
Ответ: высота дерева 12,18 м, если мы его измерим с помощью планшета.
Определим высоту дерева с помощью книжки и карандаша.
Для измерения дерева нам понадобится: книга, карандаш, рулетка. Мы измерили ширину книги и выдвинули карандаш над книгой на расстоянии 7 см. Затем мы измерили расстояние от меня до столба. Так же нам понадобилось знать рост человека до глаз (рис. 23).
C
 B D
B D
A E
Рисунок 23 - Чертёж определения высоты дерева при помощи книжки и карандаша
Дано: KD=0,15 м ширина книги, IK=0,07 м расстояние на которое выдвинут карандаш над книгой, AE=23,1 м расстояние от человека до дерева, DE=1,425 м рост человека до глаз.
Найти: АС высота дерева.
Решение: треугольники CBD и IKD подобны по двум углам. Поэтому,
,
,
AC=BC+AB=BC+DE=10,78+1,425=12,205 12,21(м).
12,21(м).
Ответ: высота дерева 12,21 м, если мы его измерили с помощью карандаша и книги.
Получив три значения высоты новогодней ёлки, мы занесли полученные данные в таблицу 1. Также мы узнали, что высота этой ёлки 12 метров..
Таблица 1 – Сводная таблица измерений высоты дерева
| Метод | Результат вычислений высоты дерева | Фактический размер дерева | Погрешность |
| С помощью планшета | 12,18 м | 12 м | +0,18 |
| С помощью зеркала | 12,07 м | 12 м | +0,7 |
| С помощью книги и карандаша | 12,21 м | 12 м | +0,21 |
Из таблицы 1 видно, что метод определение высоты дерева с помощью зеркала наиболее близок к фактической высоте ели. Так же этим методом можно производить измерения в любую погоду и вместо зеркала можно использовать лужу.
ЗАКЛЮЧЕНИЕ
В результате проведенной работы мы проанализировали литературу разных авторов по проблеме исследования. Повторили признаки подобия треугольников и разобрала решения задач различного уровня сложности, решаемые методом подобия. Эта информация поможет мне при подготовке к экзаменам. Подробно разбирая разные задачи на определение высоты предмета, мы научились видеть подобные треугольники в различных ситуациях. Мы умеем правильно записывать отношения сходственных сторон, по известным элементам, вычислять неизвестные стороны, используя свойства пропорции.
Нами было выяснено на конкретных примерах, что с помощью подобия можно найти высоту или расстояние до недоступной точки. Мы научились применять метод подобия для решения практических задач.
На наш взгляд проведённая работа практически значима, подобранный и разработанный материал может быть использовано как учениками, так и учителями, работающими в восьмых классах, по ранее обозначенной теме.
На основе практической работы был сделан вывод об истинности выдвинутой гипотезы.
Библиографический список
Атанасян Л.С., Бутузов В.Ф. Геометрия 7-9 класс. Москва: Просвещение, 2010. 384 с.
Болтянский В.Г. Элементарная геометрия. Москва: Просвещение, 1985 . 325 с.
Ганьшин В.Н. Простейшие измерения на местности.- 3-е изд. М.: Недра, 1983. – 112 с. [Электронный ресурс]. URL: http://libhist.narod.ru/Prosteishie_izmer_Ganshin.pdf (дата обращения 12.12.2017).
Глейзер Г.И. История математики в школе. Москва: Просвещение, 1982. 240 с.
Мерзляк А. Г., Полонский В. Б. Геометрия 7 класс. М: Дрофа, 2016. 193 с.
Мерзляк А. Г., Полонский В. Б. Геометрия 8 класс. М: Вентана-Граф, 2017. 208 с.
Ширина И. М. Практическое применение треугольников при измерительных работах. – Пермь, 2016. [Электронный ресурс]. URL: http://genius.pstu.ru/file.php/1/pupils_works_2016/Shirinkina.pdf (дата обращения 5.11.2017)
Энциклопедический словарь юного математика. Москва: Педагогика, 1983. 351 с.








 Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов (рис.2)[1].
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов (рис.2)[1].



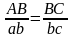 . (рис. 7)
. (рис. 7)


 дерева.
дерева.

 На рисунке 13 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10Х10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D.Наведя с помощью визиров сторону AD на вершину дерева Е и заметив деление шкалы, которое показывает отвес AF, лесник с помощью несложной формулы и находит высоту дерева [7].
На рисунке 13 изображен высотомер лесника. Он представляет собой прямоугольную пластинку размером 10Х10 см с закрепленным в точке А отвесом, шкалой на стороне ВС и визирами в точках А и D.Наведя с помощью визиров сторону AD на вершину дерева Е и заметив деление шкалы, которое показывает отвес AF, лесник с помощью несложной формулы и находит высоту дерева [7]. 
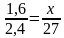 тогда,
тогда, 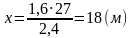
 Рисунок 15 – Задача на определение расстояния до недоступной точки
Рисунок 15 – Задача на определение расстояния до недоступной точки










