
Некоторые следствия из аксиом
Цель урока: рассмотреть следствия из аксиом, показать их применение к решению задач.
Вопросы и задания для повторения изученного ранее материала
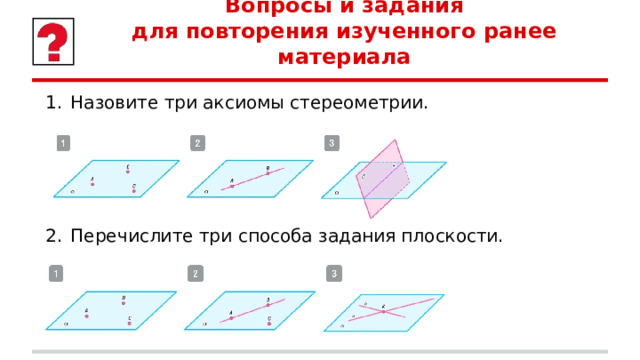
- Назовите три аксиомы стереометрии.
- Перечислите три способа задания плоскости.
Следствия из аксиом
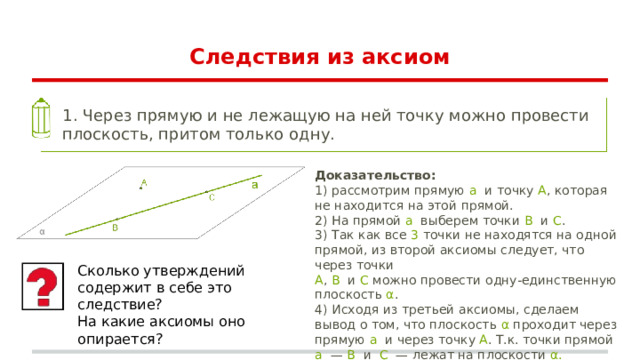
1. Через прямую и не лежащую на ней точку можно провести плоскость, притом только одну.
Доказательство:
1) рассмотрим прямую a и точку A , которая не находится на этой прямой.
2) На прямой a выберем точки B и C .
3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки
A , B и C можно провести одну-единственную плоскость α .
4) Исходя из третьей аксиомы, сделаем вывод о том, что плоскость α проходит через прямую a и через точку A . Т.к. точки прямой a — B и C — лежат на плоскости α.
Сколько утверждений содержит в себе это следствие?
На какие аксиомы оно опирается?
Следствия из аксиом
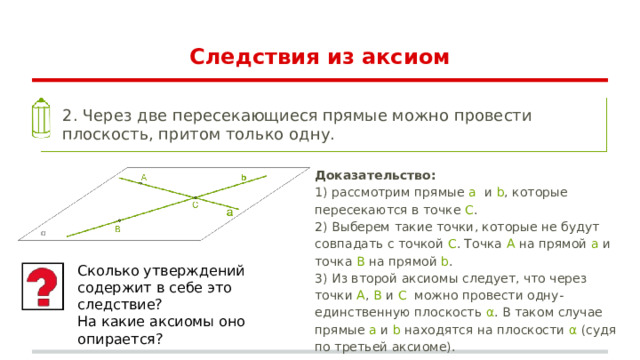
2. Через две пересекающиеся прямые можно провести плоскость, притом только одну.
Доказательство:
1) рассмотрим прямые a и b , которые пересекаются в точке C .
2) Выберем такие точки, которые не будут совпадать с точкой C . Точка A на прямой a и точка B на прямой b .
3) Из второй аксиомы следует, что через точки A , B и C можно провести одну-единственную плоскость α . В таком случае прямые a и b находятся на плоскости α (судя по третьей аксиоме).
Сколько утверждений содержит в себе это следствие?
На какие аксиомы оно опирается?
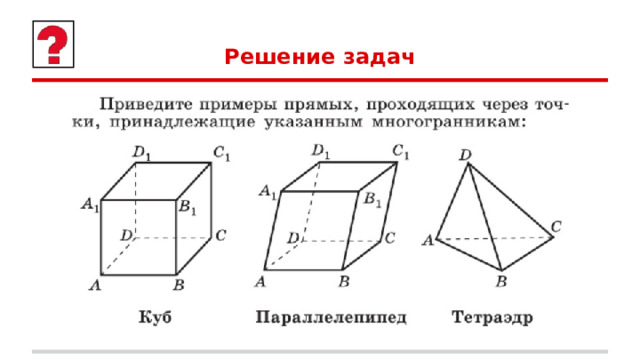
Решение задач
Решение задач (задача № 1 стр. 7)
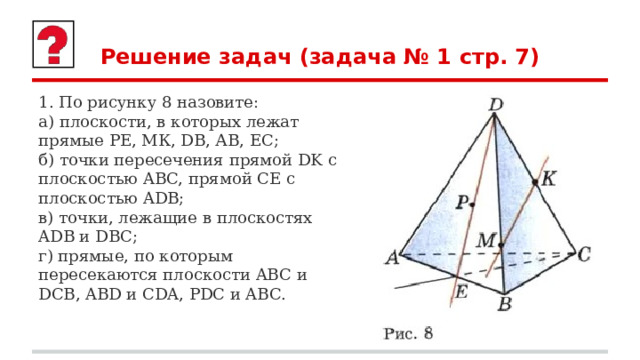
1. По рисунку 8 назовите:
а) плоскости, в которых лежат прямые РЕ, МК, DB, АВ, ЕС;
б) точки пересечения прямой DK с плоскостью ABC, прямой СЕ с плоскостью ADB;
в) точки, лежащие в плоскостях ADB и DBC;
г) прямые, по которым пересекаются плоскости ABC и DCB, ABD и CDA, PDC и ABC.

Решение задач (задача № 7 стр. 8)
Две прямые пересекаются в точке М. Докажите, что все прямые, не проходящие через точку М и пересекающие данные прямые, лежат в одной плоскости. Лежат ли в одной плоскости все прямые, проходящие через точку М?
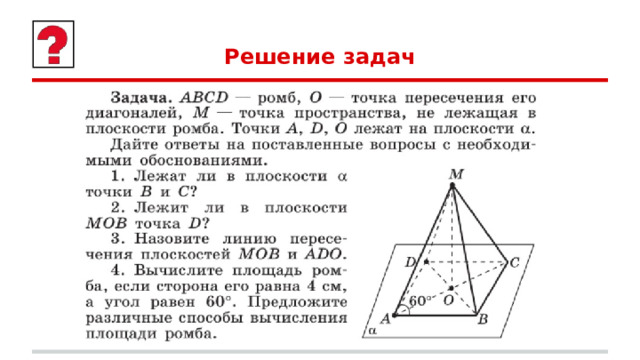
Решение задач
































