Конспект урока по алгебре в 8 классе
Тема: «Неполные квадратные уравнения.»
Разработчик урока:
учитель математики
Апалькова Г.И
Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.
Цели и задачи :
Научиться решать неполные квадратные уравнения различных видов.
Составить алгоритм для решения неполных квадратных уравнений.
Научиться находить уравнение равносильное данному.
Отработать алгоритм решения неполных квадратных уравнений.
Формируемые УУД
Познавательные: анализировать, делать выводы, сравнивать объекты по способам действий.
Регулятивные: определять цель, проблему, выдвигать версии, планировать деятельность.
Коммуникативные: излагать свое мнение, использовать речевые средства,
Личностные: осознавать свои эмоции, вырабатывать уважительное отношение к одноклассникам.
Оборудование: интерактивная доска, проектор, доска, мел, опорный конспект.
Ход урока
1. Организационный момент: Здравствуйте, я рада вас всех видеть в хорошем настроении на уроке алгебры.
2. Формулировка темы и целей урока
3. Актуализация знаний
Квадратным уравнением будем называть уравнение вида
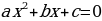 , где
, где
х – переменная,
а, b и с – произвольные числа (коэффициенты квадратного уравнения), а ≠ 0.
Число а перед х2 – первый коэффициент;
число b перед х – второй коэффициент;
третье число c – свободный член.
Названия коэффициентов сохраняются, даже если слагаемые стоят в другом порядке.
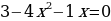
Первый коэффициент равен –4, второй –1, свободный член равен 3.
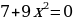
Первый коэффициент равен 9, второй равен 0, свободный член равен 7.
Квадратное уравнение, в котором коэффициент при х2 равен 1, называется приведённым квадратным уравнением.
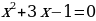

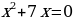
Если первый коэффициент квадратного уравнения отличается от 1, то путем деления обеих частей уравнения на этот коэффициент можно получить приведённое квадратное уравнение.
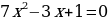 →
→ 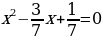
Коэффициент при х2 не может равняться нулю, иначе квадратное уравнение станет линейным.
Если хотя бы один из остальных коэффициентов будет равен 0, то в этом случае квадратное уравнение называют неполным квадратным уравнением.
Три вида неполных квадратных уравнений:
1. 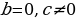 , то
, то  .
.
2. 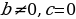 , то
, то  .
.
3. 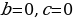 , то
, то 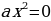 .
.
4. Первичное освоение новых знаний.
Решения уравнений таких видов
1. 
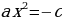 ;
; 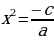
если 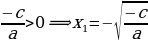 ,
, 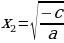 ;
;
если 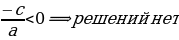 .
.
Пример 1.
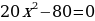 ;
; 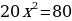 ;
; 
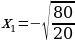 ,
,  ,
,
то есть  ,
, 
Пример 2.
 ;
; 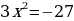 ;
; 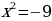 . Решений нет
. Решений нет
2. 
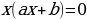 , т.е.
, т.е.  или
или
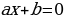 ;
; 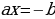 ;
;  , таким образом
, таким образом
 или
или  .
.
Пример.
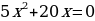 ;
;
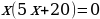 ;
;  или
или
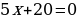 ;
; 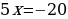 ;
; 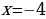 .
.
3. 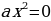

Пример.
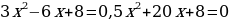 ;
;
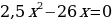 .
.
5. Первичная проверка понимания.
Самостоятельная работа с самопроверкой.
|
Вариант – 1 Решите уравнение: а) 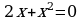 ; ; б)  ; ; в) 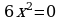 . . |
Вариант – 2 Решите уравнение: а) 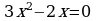 ; ; б) 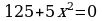 ; ; в) 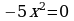 . .
|
Вариант – 3 Решите уравнение: а) 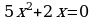 ; ; б) 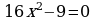 ; ; в) 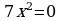 . . |
6. Первичное закрепление.
Работа с учебником: № 515, 516(а),517(а,б)
7. Контроль усвоения, обсуждения допущенных ошибок и их коррекция.
8. Подведение итогов: Предлагаю продолжить предложение «Сегодня на уроке
Я повторил …
Я закрепил …
Я научился …
Я узнал …»
Выставление отметок.
Домашнее задание № 516(б),517(в,г)
Молодцы ребята! Спасибо за урок!






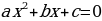 , где
, где 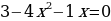
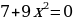
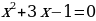

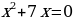
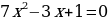 →
→ 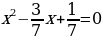
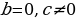 , то
, то  .
.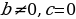 , то
, то  .
.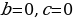 , то
, то 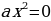 .
.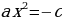 ;
; 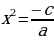
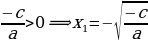 ,
, 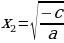 ;
;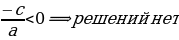 .
.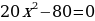 ;
; 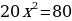 ;
; 
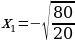 ,
,  ,
, ,
, 
 ;
; 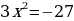 ;
; 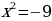 . Решений нет
. Решений нет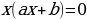 , т.е.
, т.е.  или
или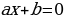 ;
; 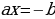 ;
;  , таким образом
, таким образом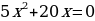 ;
;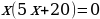 ;
; 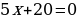 ;
; 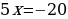 ;
; 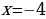 .
.
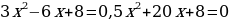 ;
;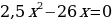 .
.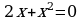 ;
; ;
;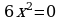 .
.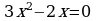 ;
;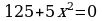 ;
;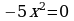 .
.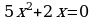 ;
;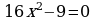 ;
;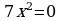 .
.









