Просмотр содержимого документа
«Нок чисел. Для уроков в 5 классе»
НОК чисел
Кратное числу «a» — это число, которое само делится на число «a» без остатка.
Числа кратные8(то есть, эти числа разделятся на8 без остатка): это числа16, 24, 32…
Кратные9: 18, 27, 36, 45…
Чисел, кратных данному числу a бесконечно много, в отличии от делителей этого же числа. Делителей — конечное количество.
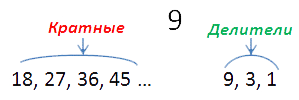
Общим кратным двух натуральных чисел называется число, которое делится на оба эти числа нацело.
Запомните!
Наименьшим общим кратным(НОК) двух и более натуральных чисел называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел.
Как найти НОК
НОК можно найти и записать двумя способами.
Первый способ нахождения НОК
Данный способ обычно применяется для небольших чисел.
Выписываем в строчку кратные для каждого из чисел, пока не найдётся кратное, одинаковое для обоих чисел.
Кратное числа «a» обозначаем большой буквой «К».
К(a) = {…, …}
Пример. Найти НОК6и8.
К(6) = {12, 18,24, 30, …}
К(8) = {8, 16,24, 32, …}
НОК(6, 8) = 24
Второй способ нахождения НОК
Этот способ удобно использовать, чтобы найти НОК для трёх и более чисел.
Разложить данные числа напростыемножители. Подробнее правила разложения на простые множители вы можете прочитать в темекак найти наибольший общий делитель (НОД).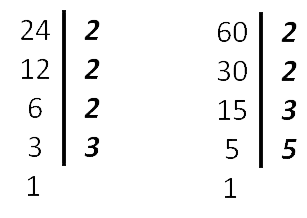
Выписать в строчку множители, входящие в разложение самого большого из чисел, а под ним — разложение остальных чисел.
Запомните!
Количество одинаковых множителей в разложениях чисел может быть разное.
60 = 2 · 2 · 3 · 5
24 = 2 · 2 ·2· 3
Подчеркнуть в разложении меньшего числа (меньших чисел) множители, которые не вошли в разложение бóльшего числа (в нашем примере это2) и добавить эти множители в разложение бóльшего числа.
НОК(24, 60) = 2 · 2 · 3 · 5 ·2
Полученное произведение записать в ответ.
Ответ: НОК(24, 60) = 120
Оформить нахождение наименьшего общего кратного (НОК) можно также следующим образом. Найдём НОК(12, 16, 24).
 24 = 2 · 2 · 2 · 3
24 = 2 · 2 · 2 · 3
16 = 2 · 2 · 2 ·2
12 = 2 · 2 · 3
Как видим из разложения чисел, все множители12вошли в разложение24(самого бóльшего из чисел), поэтому в НОК добавляем только одну2из разложения числа16.
НОК(12, 16, 24) = 2 · 2 · 2 · 3 ·2= 48
Ответ: НОК(12, 16, 24) = 48







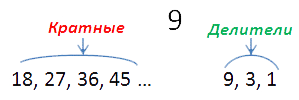
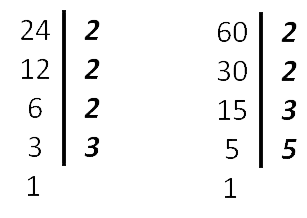
 24 = 2 · 2 · 2 · 3
24 = 2 · 2 · 2 · 3









