Россия, Энгельс
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 21.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 10.02.2025 11:49
Затеева Валентина Павловна
учитель математики
70 лет
783 122
12 
Местоположение
Специализация
Объем. 11 класс
Категория:
Геометрия
11.05.2019 23:43
Просмотр содержимого документа
«Объем. 11 класс»
ОБЪЕМ ФИГУР В ПРОСТРАНСТВЕ
Объем – величина, аналогичная площади и сопоставляющая фигурам в пространстве неотрицательные действительные числа. За единицу объема принимается куб, ребро которого равно единице измерения длины.
Для объемов пространственных фигур справедливы свойства, аналогичные свойствам площадей плоских фигур, а именно:
1. Объем фигуры в пространстве является неотрицательным числом.
2. Равные фигуры имеют равные объемы.
3. Если фигура Ф составлена из двух неперекрывающихся фигур Ф 1 и Ф 2 , то объем фигуры Ф равен сумме объемов фигур Ф 1 и Ф 2 , т.е.
V ( Ф )= V ( Ф 1 )+ V ( Ф 2 ).
Две фигуры, имеющие равные объемы, называются равновеликими.
В режиме слайдов ответы и решения появляются после кликанья мышкой
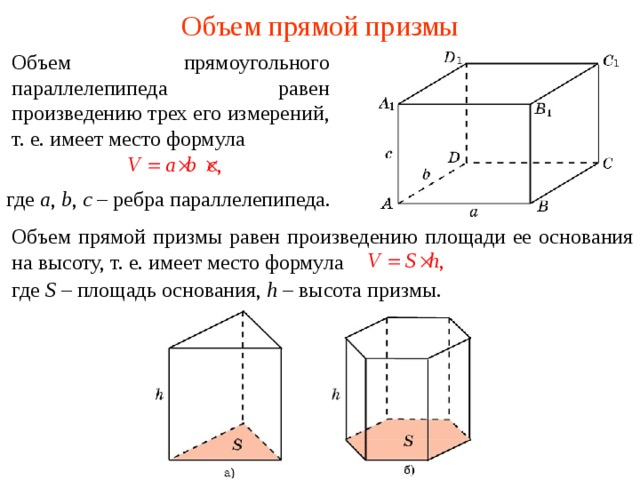
Объем прямой призмы
Объем прямоугольного параллелепипеда равен произведению трех его измерений, т. е. имеет место формула
где a , b , c – ребра параллелепипеда.
Объем прямой призмы равен произведению площади ее основания на высоту, т. е. имеет место формула
где S – площадь основания, h – высота призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
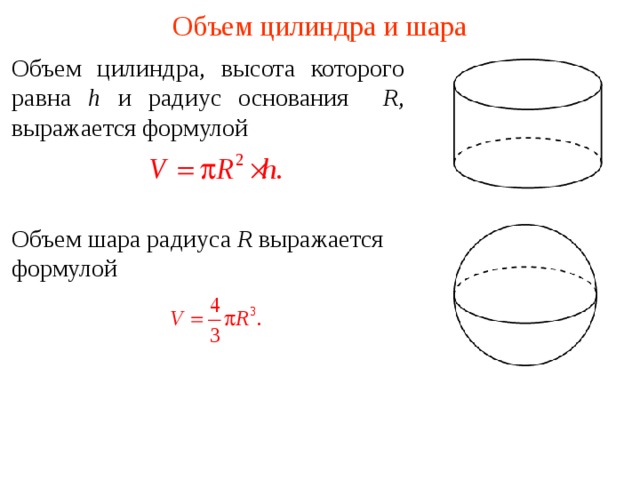
Объем цилиндра и шара
Объем цилиндра, высота которого равна h и радиус основания R , выражается формул ой
Объем шара радиуса R выражается формулой
В режиме слайдов ответы и решения появляются после кликанья мышкой
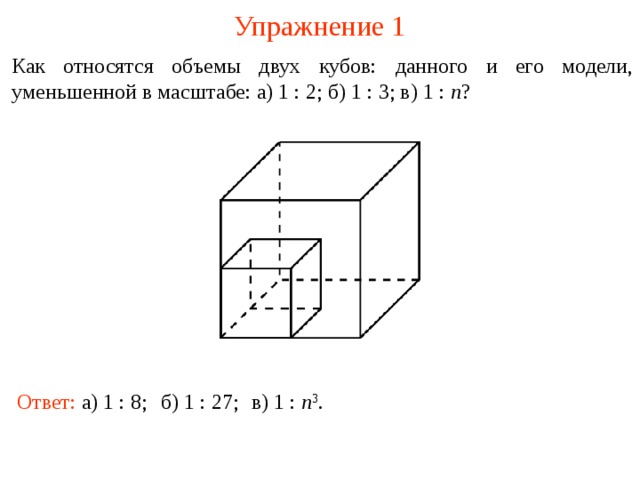
Упражнение 1
Как относятся объемы двух кубов: данного и его модели, уменьшенной в масштабе: а) 1 : 2; б) 1 : 3; в) 1 : n ?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: а) 1 : 8;
б) 1 : 27;
в) 1 : n 3 .
Упражнение 2
Площадь поверхности куба равна 24. Найдите его объем.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 8 .
Упражнение 3
Если каждое ребро куба увеличить на 2 см, то его объем увеличится на 98 см 3 . Определите ребро куба.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 3 см.
Упражнение 4
Как изменится объем прямого параллелепипеда, если: а) одно из его измерений увеличить в 2 раза, в 3 раза, в n раз; б) если два его измерения увеличить, причем каждое из них в 2, 3, n раз; в) если все три его измерения увеличить в 2, 3, n раз?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: а) Увеличится в 2 раза, в 3 раза, в n раз;
б) увеличится в 4 раза, в 9 раза, в n 2 раз;
в) увеличится в 8 раз, в 27 раз, в n 3 раз.
Упражнение 5
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3. Каким должно быть третье ребро, выходящее из той же вершины, чтобы объем этого параллелепипеда равнялся 30?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 5.
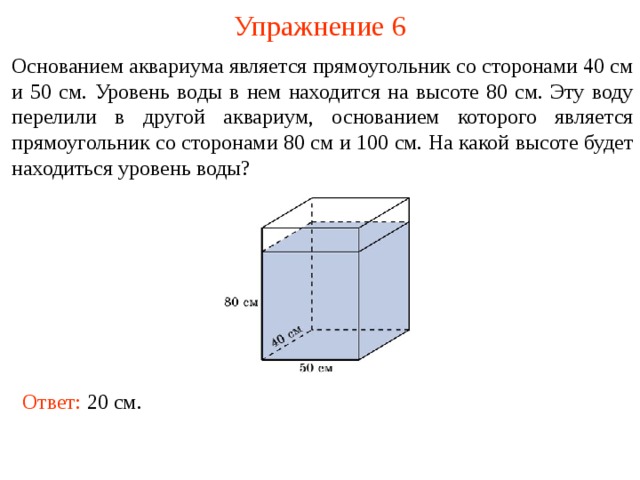
Упражнение 6
Основанием аквариума является прямоугольник со сторонами 40 см и 50 см. Уровень воды в нем находится на высоте 80 см. Эту воду перелили в другой аквариум, основанием которого является прямоугольник со сторонами 80 см и 100 см. На какой высоте будет находиться уровень воды?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см .
Упражнение 7
Сколько коробок в форме прямоугольного параллелепипеда размерами 30х40х50 (см) можно поместить в кузов машины размерами 2х3х1,5 (м)?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 150.
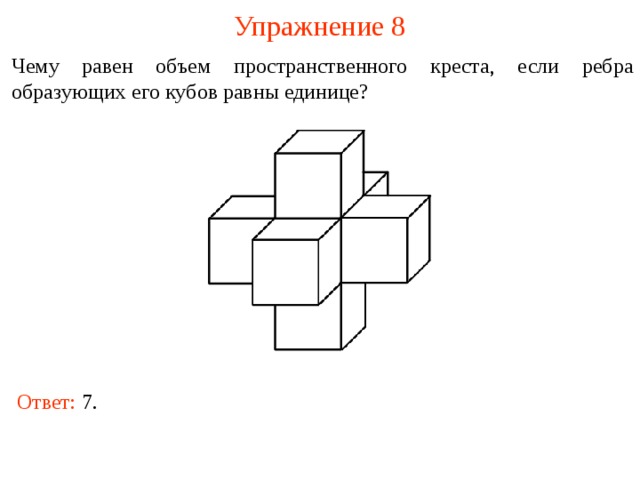
Упражнение 8
Чему равен объем пространственного креста, если ребра образующих его кубов равны единице?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 7 .
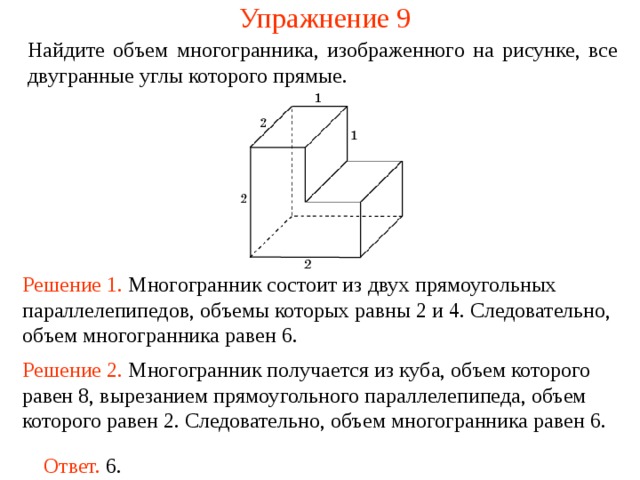
Упражнение 9
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
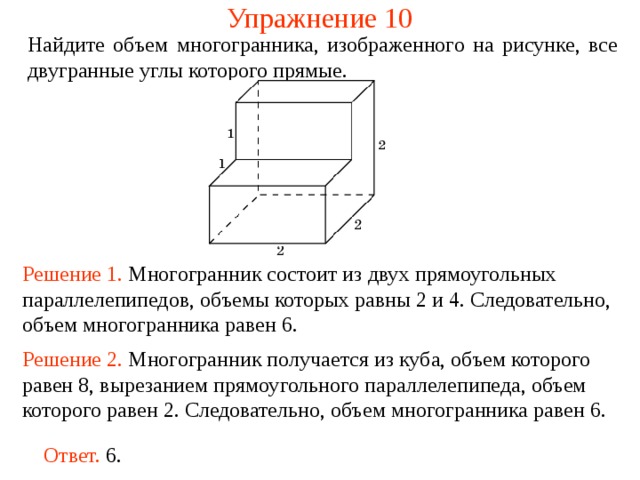
Упражнение 10
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
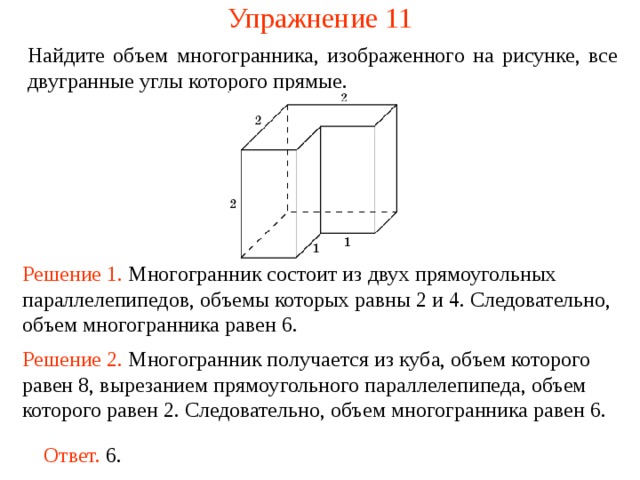
Упражнение 11
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение 1. М ногогранник состоит из двух прямоугольных параллелепипедов , объемы которых равн ы 2 и 4 . Следовательно, объем многогранника рав ен 6 .
Решение 2. М ногогранник получается из куба, объем которого равен 8, вырезанием прямоугольного параллелепипеда, объем которого равен 2. Следовательно, объем многогранника рав ен 6 .
Ответ. 6.
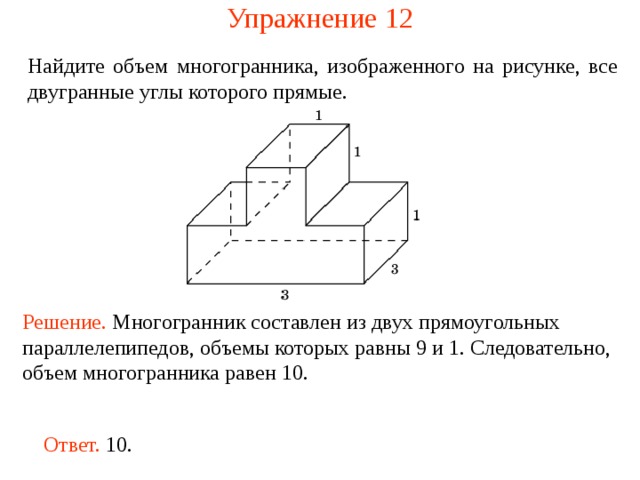
Упражнение 1 2
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник составлен из двух прямоугольных параллелепипедов, объемы которых равны 9 и 1. Следовательно, объем многогранника рав ен 10 .
Ответ. 10.
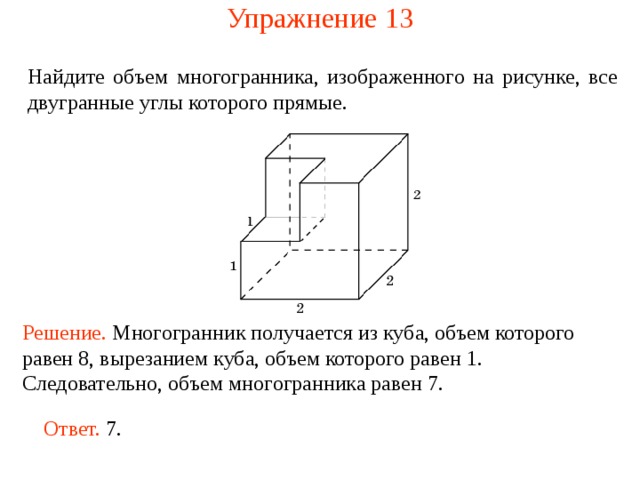
Упражнение 1 3
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из куба, объем которого равен 8, вырезанием куба, объем которого равен 1. Следовательно, объем многогранника рав ен 7 .
Ответ. 7.
Упражнение 1 4
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Решение. М ногогранник получается из прямоугольного параллелепипеда, объем которого равен 48, вырезанием прямоугольного параллелепипеда, объем которого равен 8. Следовательно, объем многогранника рав ен 40 .
Ответ. 48.
Упражнение 15
Найдите объем многогранника, изображенного на рисунке, все двугранные углы которого прямые.
Ответ. 12.
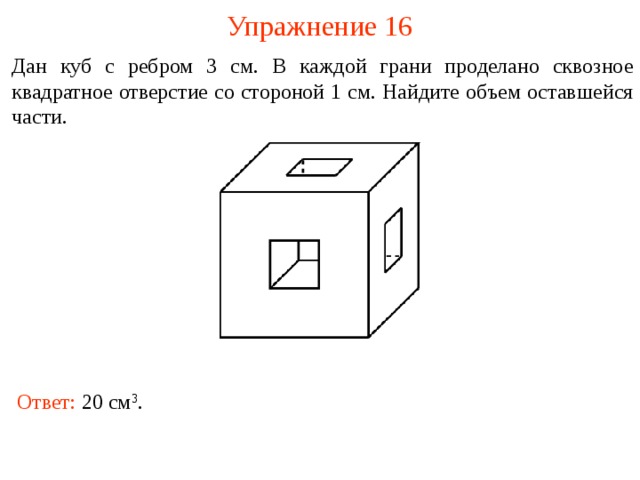
Упражнение 16
Дан куб с ребром 3 см. В каждой грани проделано сквозное квадратное отверстие со стороной 1 см. Найдите объем оставшейся части.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 20 см 3 .
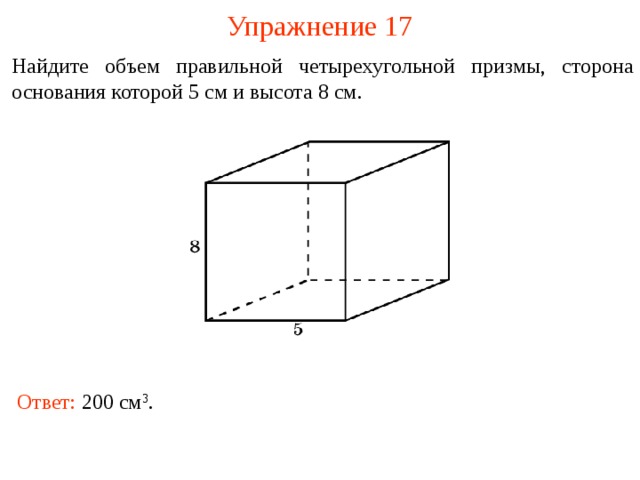
Упражнение 17
Найдите объем правильной четырехугольной призмы, сторона основания которой 5 см и высота 8 см.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 200 см 3 .
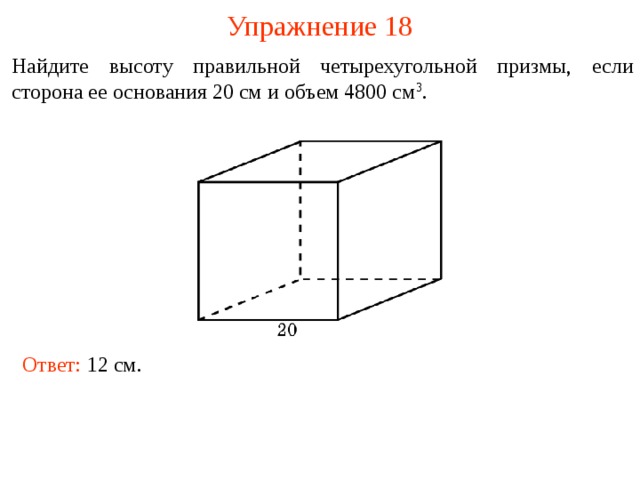
Упражнение 18
Найдите высоту правильной четырехугольной призмы, если сторона ее основания 20 см и объем 4800 см 3 .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 12 см.
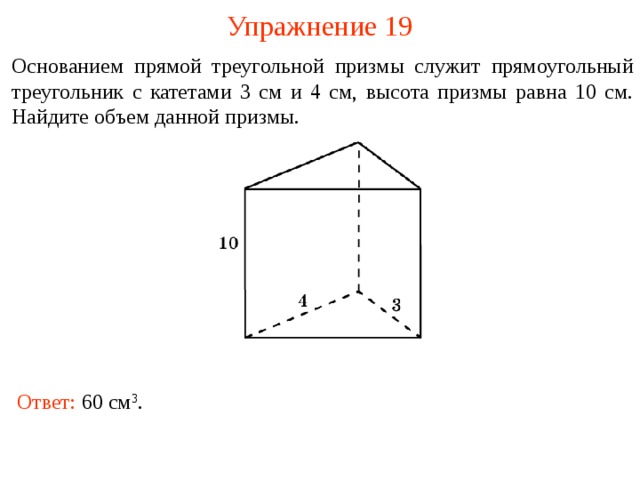
Упражнение 19
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 см и 4 см, высота призмы равна 10 см. Найдите объем данной призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 60 см 3 .
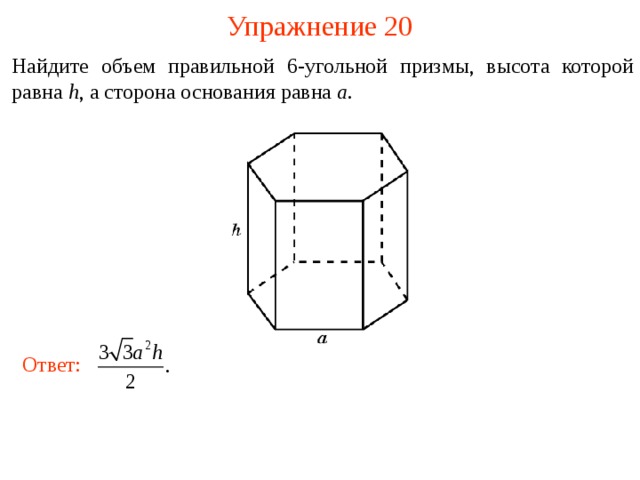
Упражнение 20
Найдите объем правильной 6 -угольной призмы, высота которой равна h , а сторона основания равна a .
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ:
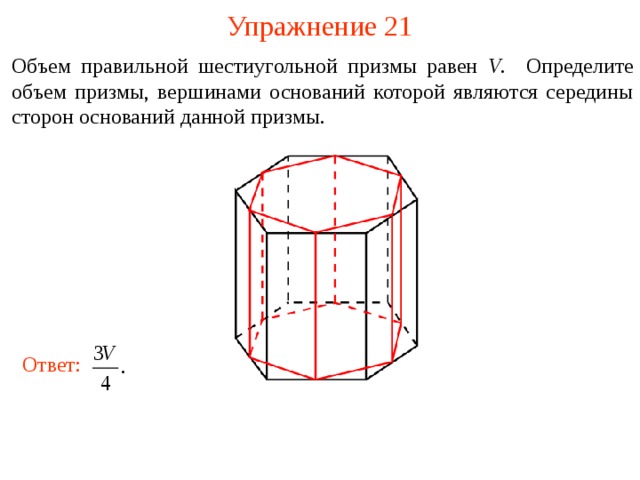
Упражнение 21
Объем правильной шестиугольной призмы равен V . Определите объем призмы, вершинами оснований которой являются середины сторон оснований данной призмы.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ:
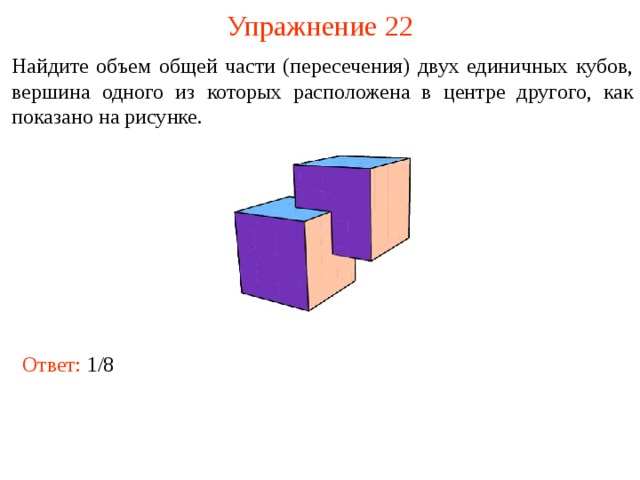
Упражнение 2 2
Найдите объем общей части (пересечения) двух единичных кубов, вершина одного из которых расположена в центре другого, как показано на рисунке.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1/8
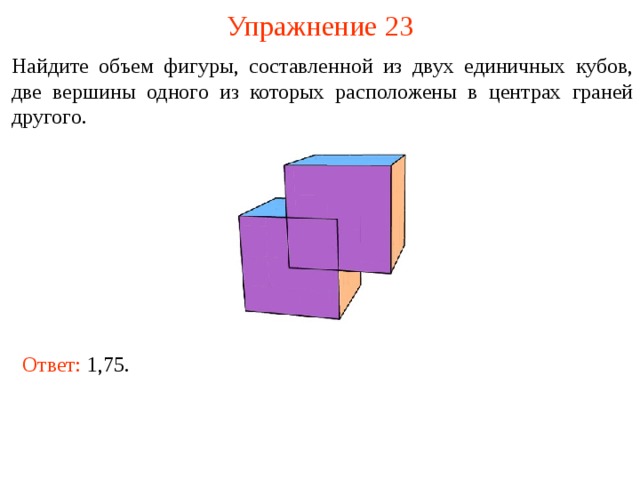
Упражнение 2 3
Найдите объем фигуры, составленной из двух единичных кубов, две вершины одного из которых расположены в центрах граней другого.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 1,75.
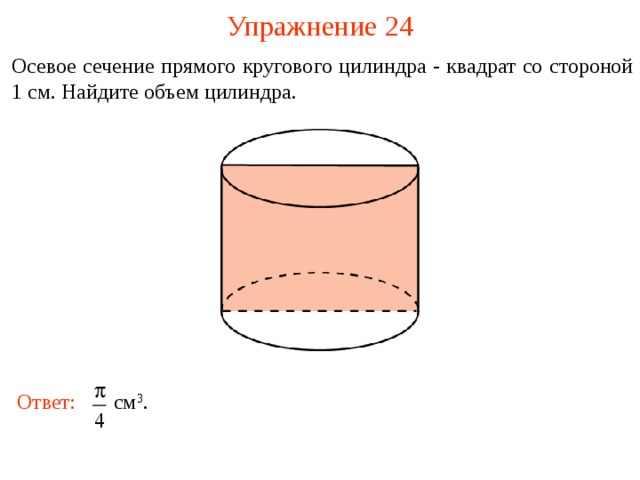
Упражнение 2 4
Осевое сечение прямого кругового цилиндра - квадрат со стороной 1 см. Найдите объем цилиндра.
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: см 3 .
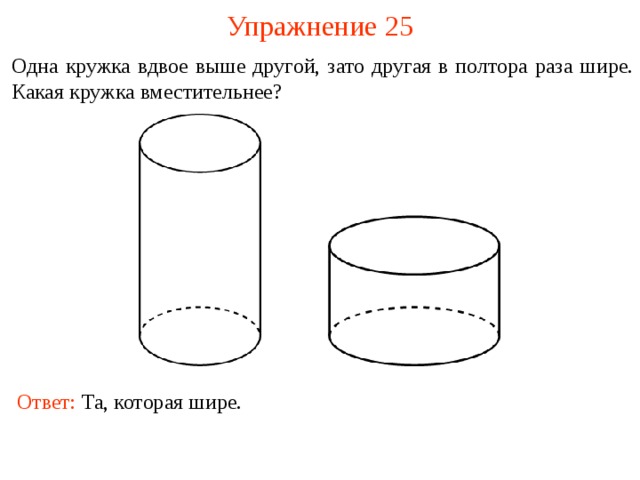
Упражнение 2 5
Одна кружка вдвое выше другой, зато другая в полтора раза шире. Какая кружка вместительнее?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: Та, которая шире.
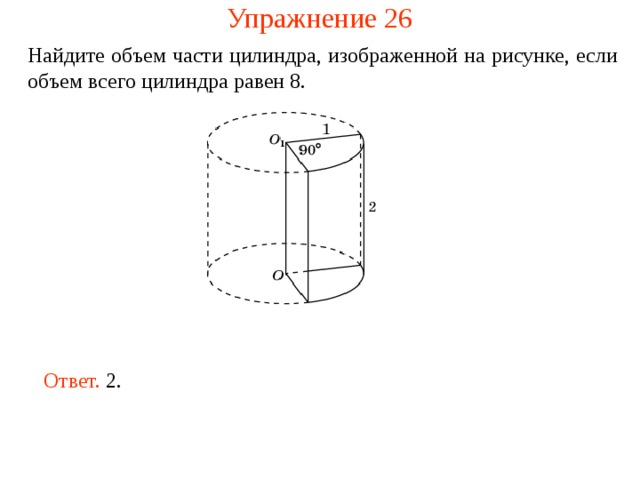
Упражнение 26
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 8.
Ответ. 2.
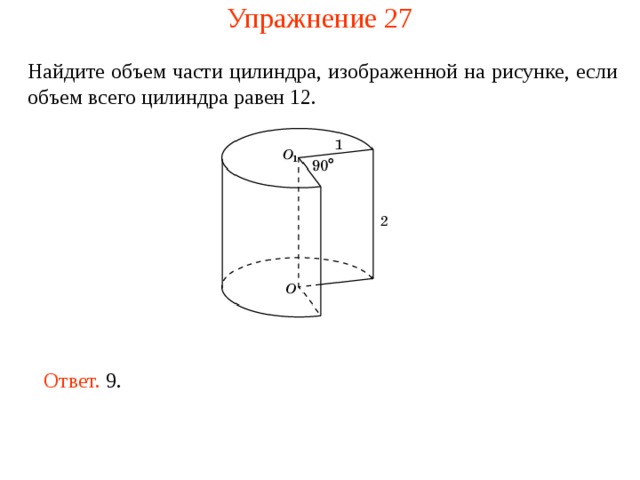
Упражнение 27
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 12 .
Ответ. 9.
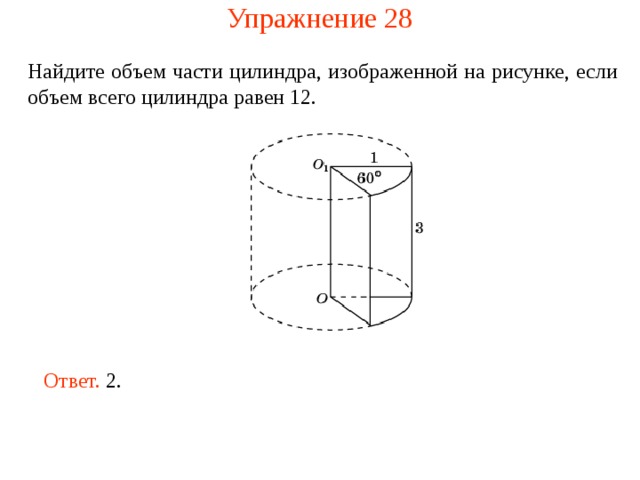
Упражнение 28
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 12 .
Ответ. 2.
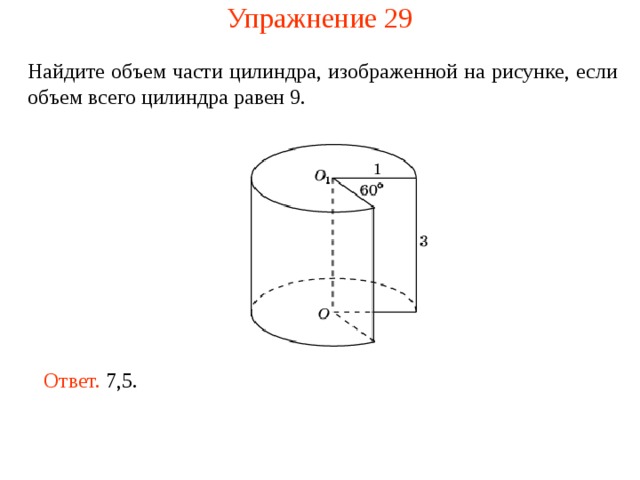
Упражнение 29
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 9 .
Ответ. 7,5.
Упражнение 30
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 4 .
Ответ. 3.
Упражнение 31
Найдите объем части цилиндра, изображенной на рисунке , если объем всего цилиндра равен 8 .
Ответ. 6.
Упражнение 32
Площадь боковой поверхности и объем цилиндра выражаются одним и тем же числом. Найдите диаметр основания цилиндра.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 4.
Упражнение 33
Во сколько раз объем цилиндра, описанного около правильной четырехугольной призмы, больше объема цилиндра, вписанного в эту же призму?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: В 2 раза.
Упражнение 34
В цилиндрический сосуд, диаметр которого равен 9 см, опущена деталь. При этом уровень жидкости в сосуде поднялся на 12 см. Чему равен объем детали?
В режиме слайдов ответы и решения появляются после кликанья мышкой
Ответ: 243 см 3 .
Упражнение 35
В цилиндрическом сосуде уровень жидкости достигает 18 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 3 раза больше первого?
Ответ. 2 см.
Упражнение 36
Объём шара равен 288 дм 3 . Найдите площадь его поверхности.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 144 дм 2 .
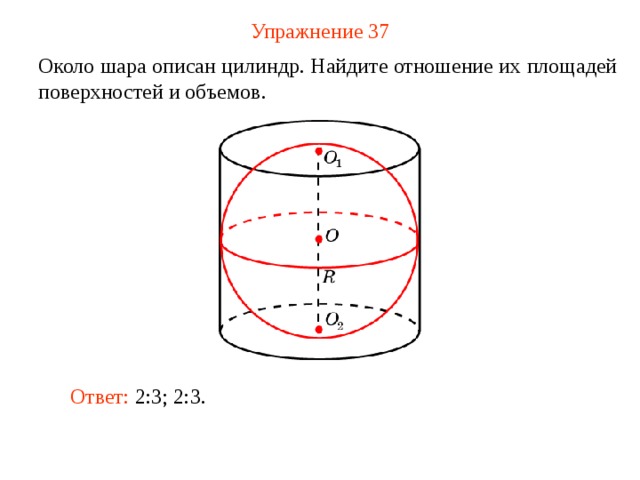
Упражнение 37
Около шара описан цилиндр. Найдите отношение их площадей поверхностей и объемов.
В режиме слайдов ответ появляется после кликанья мышкой
Ответ: 2:3; 2:3.
Упражнение 38
Вишня имеет форму шара. Диаметр косточки равен толщине мякоти. Во сколько раз объем мякоти больше объема косточки?
Решение. Диаметр вишни в три раза больше диаметра косточки. Следовательно, объем вишни в 27 раз больше объема косточки. Значит, объем мякоти в 26 раз болше объема косточки.
В режиме слайдов ответ появляется после кликанья мышкой
Упражнение 39
Одним из пространственных аналогов ковра Серпинского является губка Менгера. Она получается, если из куб разбить на 27 кубиков, вырезать центральный кубик и еще 6 кубиков, прилегающих к его граням. Затем повторить эту операцию к оставшимся кубикам и т.д. Найдите ее объем, считая исходный куб единичным.
Решение. На первом шаге выреза е тся пространственный крест, состоящий из семи кубиков, объемом 7 / 27 . На каждом следующем шаге число вырезаемых пространственных крестов увеличивается в 20 раз, а объем каждого из них уменьшается в 27 раз. Таким образом, общ ий объем вырезаемых пространственных представляет собой сумму геометрической прогрессии с начальном членом 7 /27 и знаменателем 20/27 .
По формуле суммы геометрической прогрессии находим, что это число равно единице . Следовательно, объем губки Менгера равн ен нулю.
© 2019, Затеева Валентина Павловна 6765 33
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
