Класс: 11
Предмет: геометрия
Тема урока: Объем пирамиды
Цель урока:
-
формирование навыка нахождения объема пирамиды, у которой вершина проецируется в центр вписанной окружности;
-
формирование навыка нахождения объема пирамиды, у которой вершина проецируется в центр описанной около основания окружности
Задачи урока:
Образовательные:
продолжить формирование знаний о нахождении объема пирамиды и усеченной пирамиды; систематизировать и обобщить знания по применению формул в практической деятельности;
Воспитательные:
воспитать ответственное отношение к учебе, трудолюбие, целеустремленность; объективно оценивать свои знания, осуществлять самоконтроль взаимоконтроль;
воспитание умения участвовать в диалоге, самостоятельности.
Развивающие:
развивать пространственное мышление обучающихся, умения анализировать и систематизировать материал, делать выводы, умение применять полученных в различных ситуациях, в том числе в практической деятельности
Планируемые результаты:
-
Совершенствование навыков решения задач на вычисление объема пирамиды, усеченной пирамиды;
-
развитие навыков применения формул стереометрии для решения задач; навыков вычислений и тождественных преобразований;
-
аргументированное пояснение этапов решения
Тип урока: урок обобщения и систематизации знаний
УМК: Учебник: Геометрия, 10-11: Учеб. для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов. Б. Кадомцев и др. – 11-е изд. – М.:Просвещение,2014..
Ход урока.
-
Организационный момент.
-
Приветствие
-
Создание доброжелательной атмосферы
-
Проверка готовности учащихся к уроку, психологического настроя учеников
-
Фиксирование отсутствующих
-
Проверка домашнего задания.
-
Проверить наличие письменной домашней работы у всех учащихся класса.
-
Устно проверить правильность решения задач.
-
Ответить на вопросы учащихся по домашней работе, разобрать нерешенные задачи.
-
Актуализация знаний.
Устная работа в форме теста, с проверкой у доски.
ТЕСТ:
| № | задача | Варианты ответа |
| 1 | В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение - прямоугольный треугольник с катетами 4 см и 3 см. Найдите объем призмы. | а) 10 см3 б) 42 см3 в) 60 см3 г) 30 см3 |
| 2 | В правильной шестиугольной пирамиде сторона ее основания 2 см, объем пирамиды 6 см3. Чему равна высота? | а) 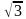 см см б) 3 см в)  см см |
| 3 | Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота? | а) 14 см б) 12 см в) 16 см.
|
| 4 | В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды? | а)  см3 см3 б)  см3 см3 в)  см3 см3 |
| 5 | В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. Найдите объем пирамиды. | а) 50 см3 б) 48 см3 в) 16 см3 |
| 6 | Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. Найти сторону основания. | а) 12 см б) 9 см в) 3 см |
| 7 | Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды. | а) 1 см б) 15 см в) 10 см |
| 8 | Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S? | а)  S S б) 3S в)  |
|
|
|
|
Таблица ответов:
| Задача | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Ответ | б | а | б | а | б | в | в | в |
-
Систематизация изученного материала
Опорные задачи:
1. Если боковые ребра пирамиды равны, то вершина пирамиды проецируется в центр окружности, описанной около основания.
2. Если боковые ребра пирамиды составляют равные углы с плоскостью основания, то вершина пирамиды проецируется в центр окружности, описанной около основания.
 Доказательство:
Доказательство:
1) ΔМАО = ΔМВО = ΔМСО = ... (равны по катету и гипотенузе или по катету и острому углу).
2) Тогда ОА = ОВ = ОС = ..., т.е. точка О - центр окружности, описанной около основания.
3. Если двугранные углы при основании пирамиды равны, то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
4. Если равны высоты боковых граней, проведенные из вершины пирамиды, то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.

Доказательство:
1) ΔМКО = ΔМЕО = ΔMFO = ... (по катету и острому углу).
2) OK = OE = OF =..., т.е. точка О - центр окружности, вписанной в основание пирамиды.
-
Контроль и коррекция знаний
Решение задач по готовым чертежам, в которых проверяется усвоение выводов, сделанных в опорных задачах.
№1
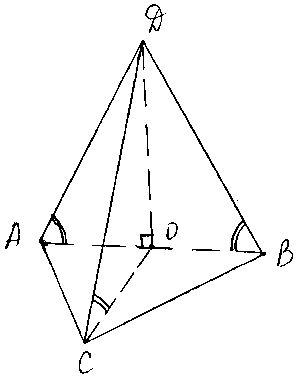
Дано: ABCD – пирамида, ΔАВС – прямоугольный, ∠С = 90°, АС = 6, ВС = 8, ∠DСO=∠DAO=∠DBO= 45°.
Найти: Vпир.
Решение:
1) Так как ∠DСO=∠DAO=∠DBO= 45°, то вершина пирамиды проецируется в центр окружности, описанной около основания.
ΔАВС – прямоугольный, значит, точка О – середина
гипотенузы, т.е. АО = ОС = ОВ.
2) ΔАВС, ∠С = 90°, тогда по теореме Пифагора: = АО = 5.
= АО = 5.
3) ΔAOD: ∠О = 90°, ∠D = ∠А = 45°, DO = OA = 5 – высота пирамиды
4) S∆ABC=  AC∙BC =
AC∙BC = 
5) Vпир.= 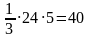
Ответ: 40.
№2

Дано: ABCD - пирамида. ΔАВС – равнобедренный, АВ = АС = 10, ВС = 12, AD = BD = CD = 15.
Найти: Vпир.
Решение:
1) Так как AD = BD = CD = 15, то вершина пирамиды проецируется в центр окружности, описанной около основания, значит, R = AO.
2) S∆ABC =  = R =
= R = 
Площадь найдем по формуле Герона: S∆ =  , где
, где 
Р = 10+10+12 = 32; S∆ABC= 48 =  .
.
3) Из ∆AOD по теореме Пифагора найдем OD =  =
=  .
.
4) Vпир.=  .
.
Ответ: 20 .
.
-
Подведение итогов урока. Рефлексия.
-
Что нового вы узнали на уроке ?
-
Достигнута ли цель урока?
-
Оцените свою деятельности и деятельности всего класса.
-
Остались ли вы довольны своей работой на уроке?
-
С каким чувством вы уходите с урока…

-
Домашнее задание
Домашняя работа будет собой представлять проверочную работу по вариантам.
I вариант
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен  . Найдите объем пирамиды.
. Найдите объем пирамиды.
2. Сторона основания правильной треугольной пирамиды равна 6 см. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
3. Основанием пирамиды служит прямоугольный треугольник с катетом 5 см и прилежащим углом  . Боковые ребра наклонены к плоскости основания под углом
. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
4. Основанием пирамиды ABCDM является равнобедренная трапеция с основаниями AD и BC острым углом  , AB = 8 см. Боковые грани наклонены к плоскости основания под углом
, AB = 8 см. Боковые грани наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
Приложение 1.
ТЕСТ:
| № | задача | Варианты ответа |
| 1 | В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение - прямоугольный треугольник с катетами 4 см и 3 см. Найдите объем призмы. | а) 10 см3 б) 42 см3 в) 60 см3 г) 30 см3 |
| 2 | В правильной шестиугольной пирамиде сторона ее основания 2 см, объем пирамиды 6 см3. Чему равна высота? | а) 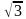 см см б) 3 см в)  см см |
| 3 | Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота? | а) 14 см б) 12 см в) 16 см.
|
| 4 | В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды? | а)  см3 см3 б)  см3 см3 в)  см3 см3 |
| 5 | В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. Найдите объем пирамиды. | а) 50 см3 б) 48 см3 в) 16 см3 |
| 6 | Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. Найти сторону основания. | а) 12 см б) 9 см в) 3 см |
| 7 | Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды. | а) 1 см б) 15 см в) 10 см |
| 8 | Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S? | а)  S S б) 3S в)  |
Приложение 2.
Проверочную домашняя работу (по вариантам0.
I вариант
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен  . Найдите объем пирамиды.
. Найдите объем пирамиды.
2. Сторона основания правильной треугольной пирамиды равна 6 см. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
3. Основанием пирамиды служит прямоугольный треугольник с катетом 5 см и прилежащим углом  . Боковые ребра наклонены к плоскости основания под углом
. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
4. Основанием пирамиды ABCDM является равнобедренная трапеция с основаниями AD и BC острым углом  , AB = 8 см. Боковые грани наклонены к плоскости основания под углом
, AB = 8 см. Боковые грани наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
_______________________________________________________________________________
Проверочную домашняя работу (по вариантам0.
I вариант
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен  . Найдите объем пирамиды.
. Найдите объем пирамиды.
2. Сторона основания правильной треугольной пирамиды равна 6 см. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
3. Основанием пирамиды служит прямоугольный треугольник с катетом 5 см и прилежащим углом  . Боковые ребра наклонены к плоскости основания под углом
. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
4. Основанием пирамиды ABCDM является равнобедренная трапеция с основаниями AD и BC острым углом  , AB = 8 см. Боковые грани наклонены к плоскости основания под углом
, AB = 8 см. Боковые грани наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
_________________________________________________________________________________
Проверочную домашняя работу (по вариантам0.
I вариант
1. Апофема правильной треугольной пирамиды равна 4 см, а двугранный угол при основании равен  . Найдите объем пирамиды.
. Найдите объем пирамиды.
2. Сторона основания правильной треугольной пирамиды равна 6 см. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
3. Основанием пирамиды служит прямоугольный треугольник с катетом 5 см и прилежащим углом  . Боковые ребра наклонены к плоскости основания под углом
. Боковые ребра наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.
4. Основанием пирамиды ABCDM является равнобедренная трапеция с основаниями AD и BC острым углом  , AB = 8 см. Боковые грани наклонены к плоскости основания под углом
, AB = 8 см. Боковые грани наклонены к плоскости основания под углом  . Найдите объем пирамиды.
. Найдите объем пирамиды.







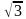 см
см см
см см3
см3 см3
см3 см3
см3
 Доказательство:
Доказательство:

 = АО = 5.
= АО = 5. AC∙BC =
AC∙BC = 
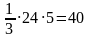

 = R =
= R = 
 , где
, где 
 .
. =
=  .
. .
. .
.


















