Объем пирамиды.

«Объем пирамиды »

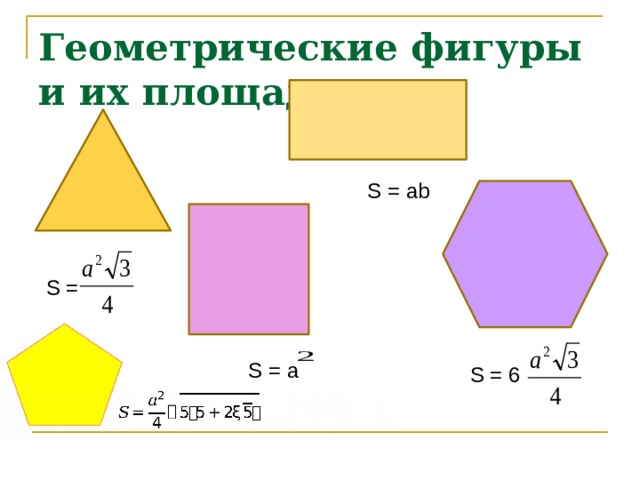
Геометрические фигуры и их площади

S = ab

S =

S = a

S = 6

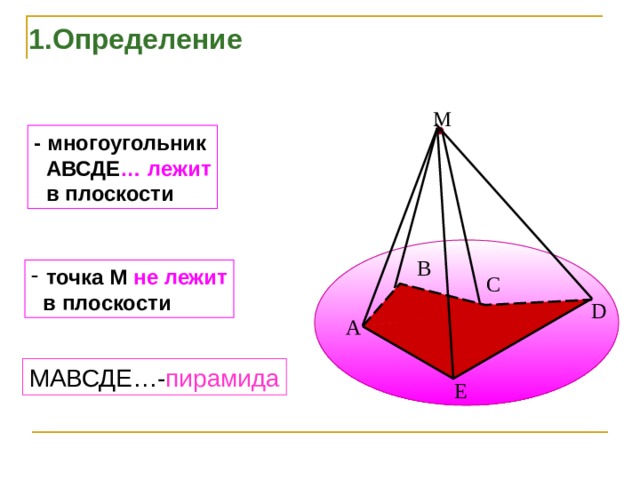
1.Определение

M

- многоугольник

АВСДЕ … лежит

в плоскости

B

• точка М не лежит

в плоскости

C

D

A

МАВСДЕ…- пирамида

E

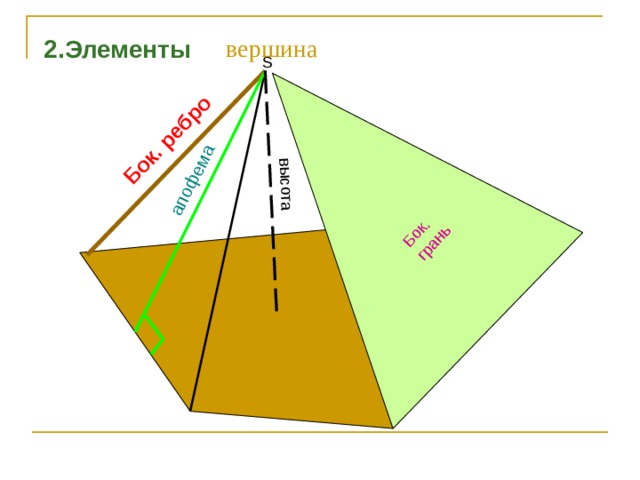
высота

апофема

Бок.

грань

Бок. ребро

вершина

2.Элементы

S

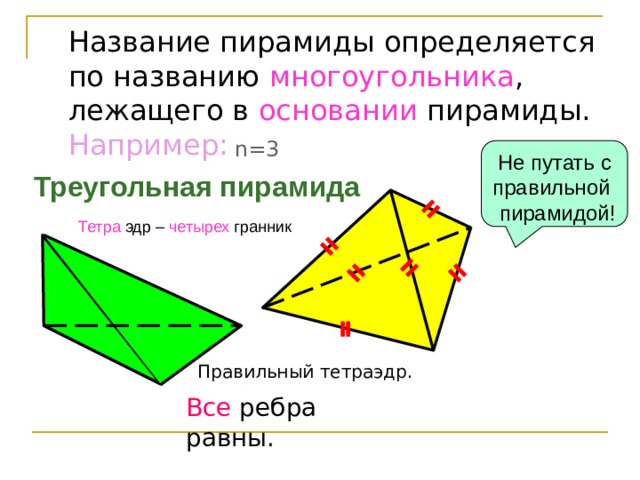
Название пирамиды определяется

по названию многоугольника ,

лежащего в основании пирамиды.

Например:

n=3

Не путать с правильной пирамидой!

Треугольная пирамида

Тетра эдр – четырех гранник

Правильный тетраэдр.

Все ребра равны.

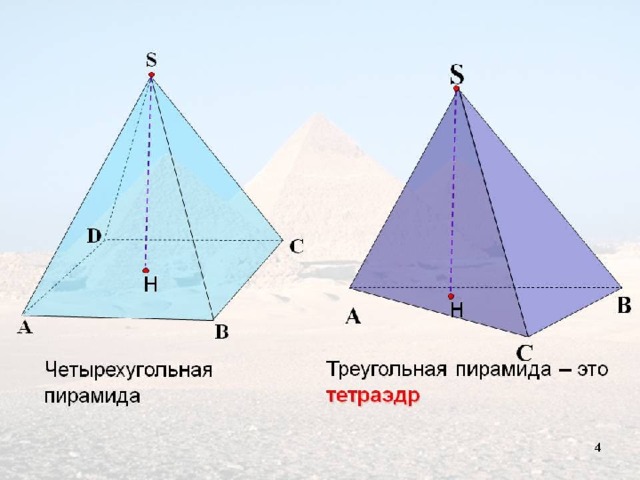
n=4

Четырехугольная пирамида

Пирамида Хеопса

в Гизе (долина царей).

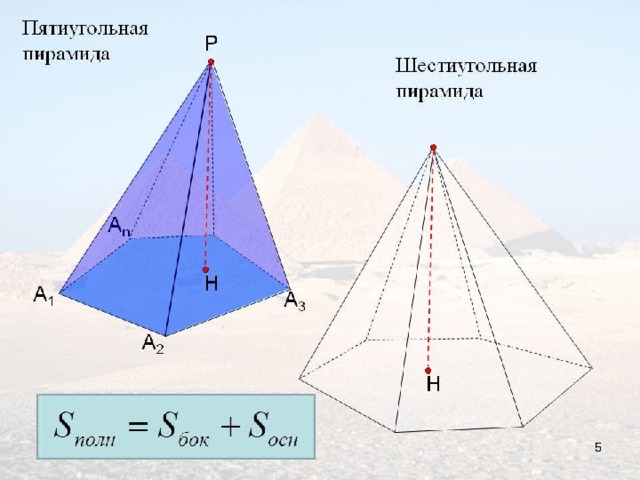
n=6

Шестиугольная пирамида

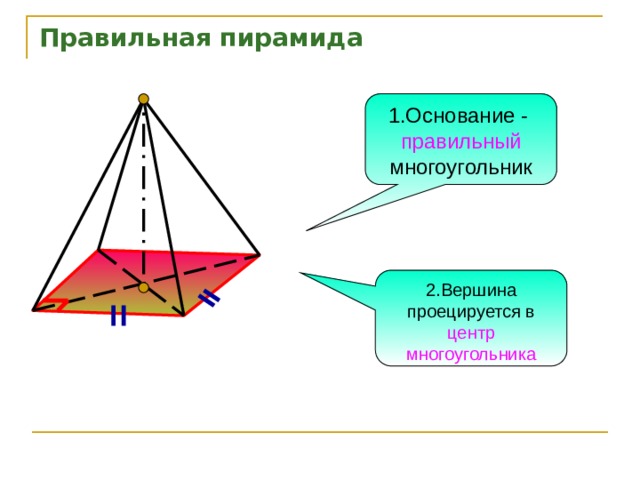
Правильная пирамида

1.Основание -

правильный многоугольник

2.Вершина проецируется в центр многоугольника

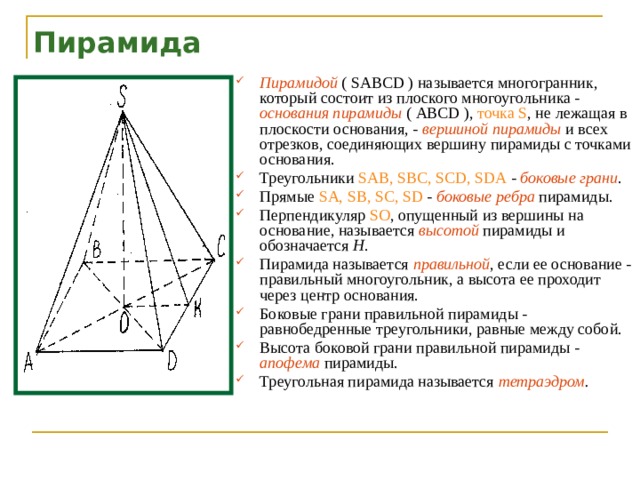
Пирамида

• Пирамидой ( SABCD ) называется многогранник, который состоит из плоского многоугольника - основания пирамиды ( ABCD ), точка S , не лежащая в плоскости основания, - вершиной пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания.
• Треугольники SAB, SBC, SCD, SDA - боковые грани .
• Прямые SA, SB, SC, SD - боковые ребра пирамиды.
• Перпендикуляр SO , опущенный из вершины на основание, называется высотой пирамиды и обозначается Н .
• Пирамида называется правильной , если ее основание - правильный многоугольник, а высота ее проходит через центр основания.
• Боковые грани правильной пирамиды - равнобедренные треугольники, равные между собой.
• Высота боковой грани правильной пирамиды - апофема пирамиды.
• Треугольная пирамида называется тетраэдром .

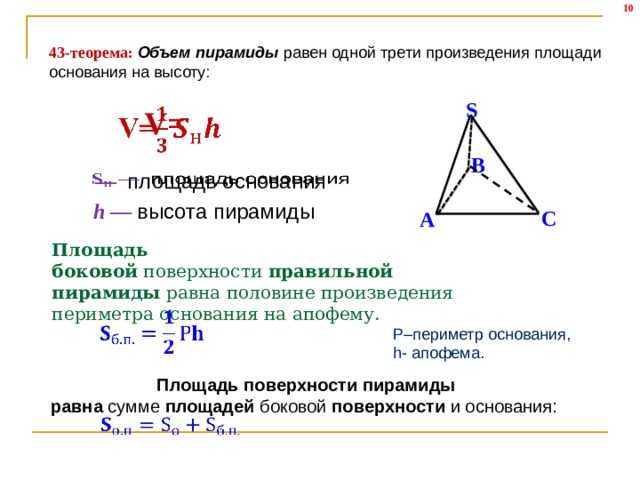
43-теорема: Объем пирамиды  равен одной трети произведения площади основания на высоту:  

S

V=

В

— площадь основания

h — высота пирамиды

С

А

Площадь боковой  поверхности  правильной пирамиды  равна половине произведения периметра основания на апофему.

Р–периметр основания,

h- апофема.

Площадь поверхности пирамиды равна  сумме  площадей  боковой  поверхности  и основания:

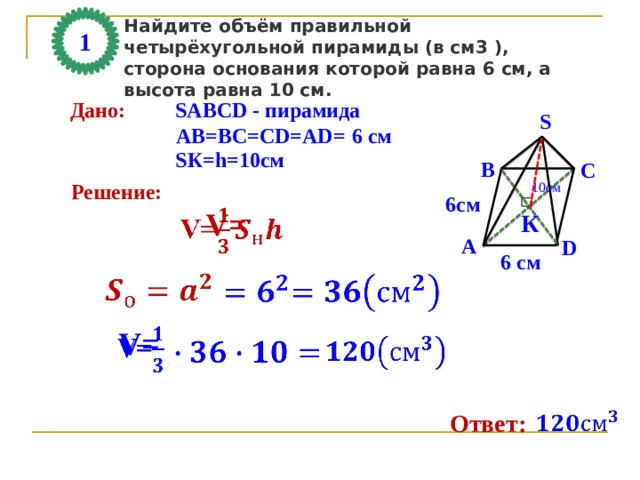
Найдите объём правильной четырёхугольной пирамиды (в см3 ), сторона основания которой равна 6 см, а высота равна 10 см.

1

Дано:

SАВСD - пирамида

S

АВ=ВС=СD=AD=

6 см

SК=h=10см

В

С

10см

Решение:

6см

V=

К

А

D

6 см

V=

Ответ:

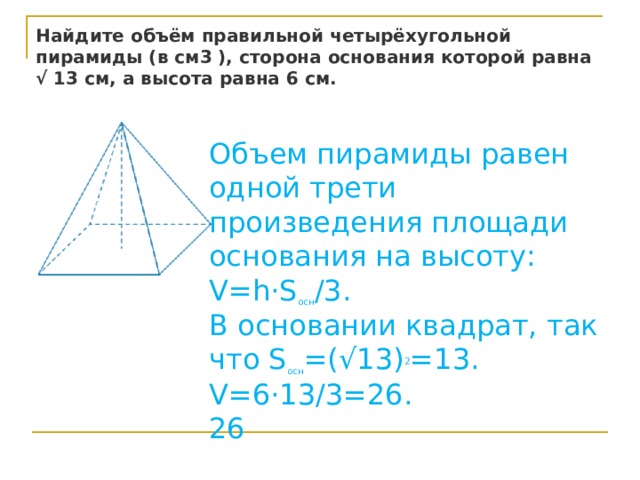
Найдите объём правильной четырёхугольной пирамиды (в см3 ), сторона основания которой равна √ 13 см, а высота равна 6 см.

Объем пирамиды равен одной трети произведения площади основания на высоту: V=h⋅S осн /3.

В основании квадрат, так что S осн =(√13) 2 =13. V=6⋅13/3=26. 26

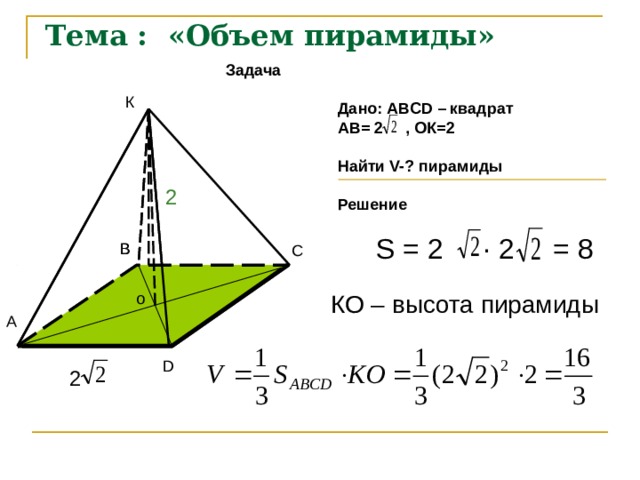
Тема : «Объем пирамиды»

Задача

Дано: АВСD – квадрат

АВ= 2 , ОК=2

Найти V-? пирамиды

Решение

К

2

= 8

S = 2 · 2

В

В

С

o

КО – высота пирамиды

О

А

D

2

Пирамиды вокруг нас

• «А в немой дали застыли пирамиды фараонов, саркофаги древней были. Величавые как вечность, молчаливые как смерть.»
• Михай Эминеску

Пирамиды с разных сторон

• Математика
• История
• Исследование мировой системы пирамид
• Исследование свойств пирамид
• Архитекторы

Математическая точка зрения

• Евклид пирамиду определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости сходятся к одной точке .
• Герон предложил следующее определение пирамиды: « Это фигура, ограниченная треугольниками, сходящимися в одной точке и основанием которой служит многоугольник ».

А под конец…

Слово «пирамида» в геометрию ввели греки, которые, как полагают, заимствовали его у египтян, создавших самые знаменитые пирамиды в мире. Другая теория выводит

этот термин из греческого слова «пирос» (рожь) – считают, что греки выпекали хлебцы, имевшие форму пирамиды

Финансовая пирамида

Домашнее задание

• Внимательно прочитайте материалы.
• Запомните элементы пирамиды. Формулы S=? V=?
• Подготовьте макет пирамиды с основанием 3,4,5,6-угольными. Сделайте необходимые измерения и Вычислите объем пирамиды. Сделайте презентацию вашему проекту.

СПАСИБО ЗА УЧАСТИЕ!