Обучение решению текстовых задач посредством моделирования

Филатова Анастасия Николаевна

учитель математики

МБОУ Новоселковская СШ

« Обучение решению текстовых задач посредством моделирования

Умение решать задачи - один из основных показателей уровня математического развития и глубины усвоения учебного материала. Действующая программа обучения математике требует развития самостоятельности у детей при решении текстовых задач.[1] Если в Государственном образовательном стандарте 2004 года в содержании изучаемой дисциплины было только указано: «Решение текстовых задач арифметическим способом (с опорой на схемы, таблицы, краткие записи и другие модели)». То в ФГОС НОО, введенном в 2011 году, выделяется отдельный раздел «Текстовые задачи», в ходе изучения которого должны быть сформированы как общее умение решать текстовые задачи, так и умение решать задачи отдельных видов. Особое внимание уделяется оценке умения учащихся осознанно работать с условием задачи.

Основная образовательная программа Спасской школы предъявляет следующие требования:

Учащийся, должен научиться использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические подсчёты; использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин; и т.д.

Из вышесказанного можно заключить, что решению задач отводится ключевое место в изучении математики. Любая контрольная работа, районный срез или областной и всероссийский мониторинг содержат в себе ряд задач, нацеленных на проверку сформированности у школьника аппарата работы с текстовой задачей. Я считаю, что для совершенствования навыков решения текстовых задач, необходимо применять метод моделирования .

Ещё в начальной школе каждый ученик должен научиться кратко записывать условие задачи, иллюстрируя его с помощью рисунка, схемы или чертежа, обосновать каждый шаг в анализе задачи и её решении, проверить правильность найденного решения. Однако на практике приходится наблюдать, что некоторые учителя в начальной школе предпочитают не тратить время на составление схем или краткой записи, что зачастую приводит к несформированности у учащихся необходимых умений.

Опыт показывает, что обучение решению задач с применением моделирования активизирует мыслительную деятельность учащихся, помогает им понять задачу, самостоятельно найти рациональный путь её решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет ученикам яснее увидеть зависимости между данными и искомыми величинами и оценить задачу вцелом, а учителю - продемонстрировать разные варианты решения и, сравнив их, обобщить теоретические знания. Верно отмечено, что постановка учебной задачи составляет мотивационно-ориентировочное звено-первое звено учебной деятельности. Вторым (центральным) звеном является исполнительское, оно включает в себя ряд учебных действий по решению задачи:

• Преобразование условий предметной задачи с целью выявления в ней основного отношения;

• Моделирование выделенного отношения в предметной, графической или буквенной форме;

• Преобразование модели для изучения свойств отношения;

• Построение системы частных задач, решаемых общим способом.

В седьмом классе учащиеся практически перестают пользоваться арифметическим способом решения задач (т.е. по действиям, с последовательным аргументированием выполненного шага), как только изучат алгебраический (посредством составления уравнений, их систем, неравенств и т.д.). Хочется сразу заметить, что крайне важно научить школьника арифметическому методу решения задач. Так как он развивает мышление, математическую грамотность. Учащийся, решая задачу по действиям, анализирует каждый шаг, а в конце решения выполняет синтез. В алгебраическом методе наоборот, он идет от синтеза к анализу. Но как научить ребёнка анализировать сложную задачу, состоящую из нескольких действий? В большинстве случаев, с простой задачей (в одно действие) справляются успешно все учащиеся класса, а вот с составной, содержащей по сути несколько простых, только часть класса.

Со слов В.В. Давыдова «Чтобы научить учащихся самостоятельно и творчески учиться нужно включать их в специально организованную деятельность, сделать хозяевами этой деятельности. Одним из способов включения учащихся в активную деятельность в процессе решения задач является моделирование». [2]

Чтобы выяснить, как усваиваются и совершенствуются учениками 5 класса навыки решения текстовых задач, я предложила ученикам письменную работу. Каждый ученик должен был решить две задачи. Решение задачи учащиеся оформляли произвольно.

Проверяя работы, я поделила их на две группы. В первую стопку сложила работы, в которых составлена модель задачи, во вторую стопку - тетради учащихся, решавших задачи не прибегая к методу моделирования. На работу было отведено 20 минут, однако некоторые учащиеся справились с заданием быстрее. Рассмотрим ряд из предложенных детям задач и варианты ошибочных решений к ним.

Задача №1. Летом 2015 года стояла хорошая погода. Однажды, после тёплого грибного дождя Жанна, Вова и Ира отправились в лес по грибы. Жана нашла 103 гриба, Вова на 18 больше, чем Жанна, а Ира на 64 гриба меньше, чем Жанна и Вова вместе. Сколько грибов собрали дети вместе?

Решение:

1. 103+18= 121(г)

2. 103+121=224(г)

3. 224-64=160(г)

4. 224+160=384(г)

Ошибочные решения:

1 вариант:

1. 103-18=85 (г)

2. 103+85=188 (г)

3. 188+64=252 (г)

2 вариант:

1. 103+18=121 (г)

2. 121-64=57(г)

3. 121+57=178(г)

3 вариант:

1. 103+18=121(г)

2. 103+121=224(г)

3. 103-64=39(г)

4. 224+39=263(г)

Я привожу наиболее характерные ошибки, встретившиеся в работах учащихся, не учитывая вычислительные ошибки. На этом примере уже можно проследить, что ученик терял логику рассуждений уже во втором действии. Это могло быть следствием невнимательного чтения задачи, либо не сложившейся картины в воображении школьника. Забегая вперёд, отмечу, что это примеры ошибочных решений из тетрадей второй стопы. Встретилась ошибка и в решении с составленной моделью к задаче, но ошибка была и в самой модели. Что говорит о несформированности умений работы с моделью задачи.

Задача №2. В три магазина завезли 3840 кг сахарного песка. После того как первый магазин продал 568 кг сахарного песка, второй 624 кг и третий 401 кг, сахара осталось во всех магазинах поровну. Сколько килограммов сахарного песка получил каждый магазин?

Решение:

Конечно задача, состоящая из семи действий затруднительна для 5 го класса, она требует внимания и рассудительности. Опять же немало ошибок было допущено пятиклассниками. Приведу в пример несколько ошибочных решений: Вариант1:

1. 568+624=1192 (кг)

2. 1192+401=1593 (кг)

3. 3840-1593=2247 (кг)

4. 2247:3=749 (кг)

Вариант 2 :

1. 3840-568=3272 (кг)

2. 3840-624=3216 (кг)

3. 3840-401=3439 (кг)

Вариант 3:

1. 3840:3=1280 (кг)

2. 1280+568=1848 (кг)

3. 1280+624=1904 (кг)

4. 1280+401=1681 (кг)

Вариант 4:

1. 3840-568= 3272 (кг)

2. 624-401=223 (кг)

3. 3272 -223=3049 (кг)

Последние варианты решения задачи наглядно демонстрирует, что пятиклассники не смогли чётко представить жизненную ситуацию, явившуюся сюжетом задачи, а просто механически манипулировали числами. Зачастую, на уроке учитель стремится успеть решить как можно больше задач, что не всегда обосновано. Ведь в большинстве своём «слабый» ученик успевает лишь записать решение задачи, предложенное одним из способных одноклассников. На осмысление составленной записи ему просто не хватает времени. На письменной самостоятельной работе такой ученик теряется, он не научен рассуждать. Решение составной задачи для него оказывается непосильным. Мои наблюдения и анализ проделанной работы подсказывают, что основной причиной, по которой дети допускают ошибки, при решении текстовых задач, является отсутствие её схематического изображения. Разобрав задачу «по полочкам», изобразив её модель на чертеже или схеме, ученик способен её глубоко понять и проанализировать.

В широком смысле слова моделирование- это замена действий с реальными предметами действиями с их образами, моделями, муляжами, макетами, а так же чертежами, схемами и т.д. [1]

Чертёж представляет собой так же условное изображение предметов и взаимосвязей между ними, выраженное графически с помощью отрезков с соблюдением определённого масштаба. Наглядность, особенно графическая , необходима на протяжении обучения как важное средство развития более сложных форм конкретного мышления и формирования представлений о математических понятиях. Как отмечает Л.Ш. Левенберг, рисунки, схемы и чертежи не только помогают учащимся в сознательном выяснении скрытых зависимостей между величинами, но и побуждают детей активно мыслить, искать наиболее рациональные пути решения задачи, помогают не только усваивать знания, но и овладевать умениями применять их.

Составить модель к первой задаче, при работе над ошибками, ребята смогли достаточно быстро и скорректировали своё решение. А вот ко второй задаче - затруднились. В процессе её разбора, мы совместно с учащимися составили схематический чертёж:

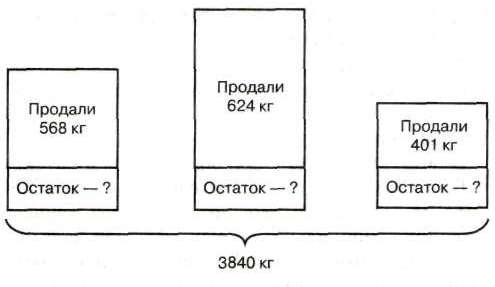Я предложила ребятам, используя отрезки, составить новую модель той же задачи. Затратив некоторое время большая часть класса справилась и с этим заданием. Получилось примерно так:

Такая модель помогает уяснить одно из важных условий задачи, которое вызвало наибольшее затруднение в решении, а именно: после того, как в каждом магазине продали часть завезённого сахарного песка, в каждом из них сахара осталось поровну.

Теперь даже «слабому» ученику задача оказалась ясна и посильна. Замечу, что выполняя самостоятельно решение задачи, после составления модели, мы отыскали 6 способов решения этой задачи.

На этом примере можно увидеть, что графическая модель задачи позволяет предупредить ошибки в решении. Она также создаёт условия для активной мыслительной деятельности в поисках разных способов решения одной и той же задачи. Такой поиск способствует развитию у школьников вариативности мышления.

Сделав выводы о проделанной письменной работе, я решила продолжить обучение решению текстовых задач в 5 классе, опираясь на метод моделирования. В первую очередь, мне необходимо было научить вдумчивому вчитыванию в текст задачи. Для составления модели задачи, нужно так же обладать знаниями умениями и навыками работы с геометрическими фигурами: отрезком, прямоугольником , кругом и т.д.

Таким образом применение метода моделирования при решении задач, позволяет отточить знания по другим разделам математики.

Где же взять столько времени, чтобы к каждой задаче продумать схему или чертёж? Я нашла несколько вариантов использования метода моделирования на разных этапах урока и в домашнем задании.

Совместно с учащимися 5 «Б» класса мы придумали проект. Его суть состоит в создании сборника задач. Каждый учащийся завёл блокнот, или тетрадь, в которой он занимается математическим творчеством. Иногда (после изучения ключевых параграфов), учащиеся получают творческое домашнее задание. Например составить задачу по схеме или задачу, решаемую в три действия, каждое из которых является вычитанием, либо , наоборот, придумать схему, к которой можно составить задачу на движение и пр. Составляя тексты задач, чертежи, учащиеся начинают глубже понимать их. Встретив в учебнике задачу, подобную той, что ученик сам составил, он с лёгкостью использует знакомый алгоритм рассуждений.

Учащиеся с удовольствием выполняют подобного рода домашние задания. Их сборники насыщены яркими иллюстрациями к задачам, которые впоследствии мы используем, как дополнительный дидактический материал, т.е. вместо карточек. Тем интереснее школьникам. Они стремятся придумать, что-то особенное, сложное и оригинальное. Вот несколько примеров из сборников учащихся.

На уроке изучения нового материала, я показываю, несколько примеров моделей нового типа задач. Когда переходим к первичному закреплению, добиваюсь, чтобы все учащиеся составили модель задачи самостоятельно, и только после этого, прошу записать решение на доске кого- то из ребят.

Возьмём, к примеру, задачи на движение из учебника математики А.Г. Мерзляка № 940 и № 938, в которых приходится находить скорость сближения или удаления.

Рассуждая привычно, учащиеся предлагают решение в три действия:

1. 63,4*9,3=589,62 (км) путь первого поезда

2. 58,6*9,3=544,98(км) путь второго поезда

3. 589,62+544,98=1134,6 (км)

Когда я ввожу понятие скорости удаления двух тел, обязательно использую чертёж. Учащиеся, взглянув один раз на него, легко запоминают, как решить подобную задачу в два действия.

63,4 км/ч

58,6 км/ч

9,3 ч

1. 58,6+63,4=122(км/ч) скорость удаления друг от друга

2. 122*9,3=1134,6 (км)

Графическая модель задачи даёт исчерпывающее представление о соотношении данных величин.

Задача № 940 немного сложнее, но так же безошибочно решается учащимися после составления модели.

В 6,3 р больше

13,8 км/ч

4,5 ч

1. 13,8 *6,3=86,94( км/ч) скорость легкового автомобиля

2. (13,8+86,94)* 4,5=453,33 (км) расстояние между городами.

В учебнике И.И, Зубаревой, А.Г. Мордковича, встречаются учебные задания, развивающего значения. Они помогают самостоятельно прийти к какой либо закономерности, правилу; и подкрепляются схематическим чертежом. Вот например:

Ещё одна находка в работе с моделированием, это проверка домашнего задания с помощью документкамеры. Я заготавливаю заранее модель задачи с ошибкой и прошу ребят её найти. Этот приём годится и в устной работе с классом.

Нельзя не затронуть ещё один раздел математики, который введён в школьный курс не так давно, но до сих пор вызывает много вопросов и дискуссий, задачи с вероятностным содержанием. Они включены в выпускной экзамен как основной так и средней школы, поэтому должны быть представлены учителем в доступной форме. Это потребует от учителя использования новых методических подходов, технологий и видов деятельности.

Вычисление вероятности случайного события должно начинаться с обсуждения случайного опыта и его возможных исходов, с обоснования их равно-(или, наоборот, не равно-)возможности. Построенное в результате множество элементарных исходов с распределением вероятностей на нём и составляет математическую модель случайного опыта. Как показывает учебная практика, именно этот этап решения вероятностных задач вызывает у учащихся наибольшие трудности. Они не могут перечислить возможные исходы опыта, придумать удачный способ их обозначения(кодирования); понять, какие детали эксперимента важны, существенны, а какие нет; попытаться свести данную ситуацию к одной из изученных ранее. А ведь это и составляет суть математического моделирования, о котором говорилось ранее.

В 5 классе я использую опять же моделирование на плоскости с использованием простых геометрических фигур. Приведу несколько примеров:

1. Задача о дежурстве

Одноклассницы Оля, Валя и Катя дежурят по школе. Сколькими способами классный руководитель может расставить девочек по одной на каждом из этажей школы?

Можно занести данные в таблицу и перебрать тем самым все возможные варианты.

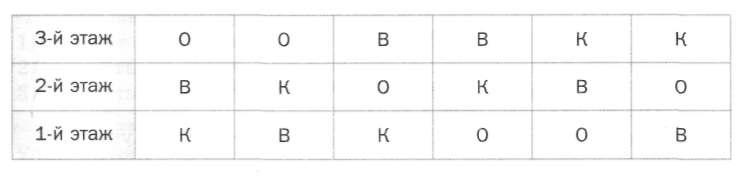
Либо использовать граф:

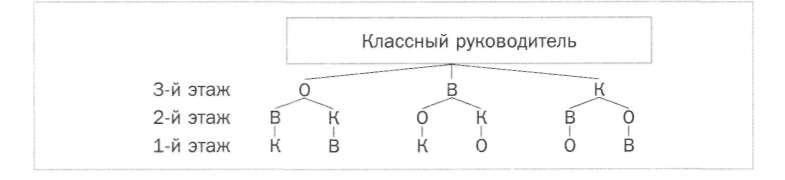
1. Задача о рукопожатиях

При встрече четыре приятеля обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Обозначим буквами А,B,C, D приятелей, которые обменялись рукопожатиями. Схематично это можно изобразить например так:

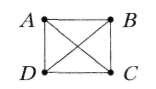Посчитав полученные отрезки находим ответ- 6 рукопожатий.

В седьмом классе можно уже предложить использовать ИКТ технологии, которые в последние годы всё глубже проникают в школьную жизнь, не обходя стороной и математику. Теория вероятности и математическая статистика как раз те разделы математики, в которых компьютер может оказать неоценимую помощь. Существуют виртуальные лаборатории, которые позволяют моделировать, сюжеты вероятностных задач. Авторы такого цифрового ресурса небезизвестные математикам Бунимович Е.А, Булычёв В.А.[2] Их инновационный учебно-методический комплекс можно найти в единой коллекции цифровых образовательных ресурсов. (http://school-collection.edu.ru)

Компьютер, как никакое другое средство обучения, способен наглядно продемонстрировать правильность или неправильность выбранной модели, избавить от рутинных экспериментов и вычислений. Приведу пример такого использования, предложенный в электронном пособии.

В ящике лежат 4 одинаковых пары перчаток. Из него наугад выбирают 4 перчатки. С какой вероятностью из них можно образовать две пары?

Задачу можно решить аналитически, используя сочетания: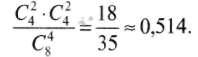

Но чтобы подвести учащихся к самостоятельному получению этого результата, можно им предложить сгенерировать подобную ситуацию в виртуальной лаборатории. В их распоряжении окажутся традиционные для вероятностных задач наборы генераторов случая, такие как монетка, кубик, разноцветные шары и т.д. Переход от четырёх одинаковых пар перчаток к восьми шарам- это уже первый этап моделирования. При этом четыре шара одного цвета соответствуют левым перчаткам, четыре другого цвета -правым.

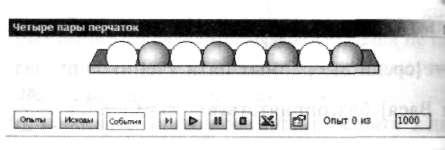
Дальше ученикам предстоит задать схему выбора- одновременный или последовательный, с возвращением или без. Затем им нужно провести ряд экспериментов в лаборатории и наблюдать за изменением частоты события.

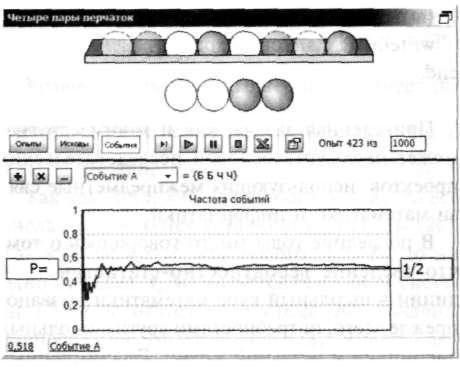
В этой задаче она колеблется около ½. Но будет ли это точным значением вероятности? Для ответа на этот вопрос лаборатория позволяет рассмотреть различные системы исходов опыта, проанализировать их равновозможность, прийти к правилам их подсчёта и получить точный результат, приведённый выше.

Хочу порекомендовать метод моделирования при решении текстовых задач своим коллегам. Считаю, что наглядно- образное мышление учащихся начальной школы, не может в один миг (при переходе в среднее звено) стать абстрактным. Следует развивать умения школьников по работе с задачей для достижения высоких результатов изучения школьного курса математики.

Список литературы

1. «Математика в школе», №3, 2009г., изд. «Школьная Пресса»

1. «Математика в школе», №5, 2008г., изд «Школьная Пресса»

1. Математика: программы: 5-11 классы/[А.Г. Мерзляк, В.Б.Полонский, М.С. Якир и др.].-М.: Вентана-Граф, 2015.-152с.

1. Математика: 5 класс: учебник для учащихся общеобразовательных организаций/ А.Г.Мерзляк, В.Б. Полонский, М.С. Якир.-2-е изд., перераб.-М.: Вентана- Граф, 2016.-304с.:ил.

1. Математика. 5 класс: учеб. Для учащихся общеобразоват. учреждений/И.И. Зубарева, А.Г. Мордкович.-11-е изд., стер.-М.: Мнемозина, 2011.-270с.: ил.

1. http://school-collection.edu.ru/catalog/rubr/a1a47299-4962-459e-9cac-b48c23159c3a/114285/?