ОГЭ-2021: Основные сведения, требования, ресурсы для подготовки

ГИА - Государственная итоговая аттестация ОГЭ - Основной государственный экзамен

Подготовка к ОГЭ

2020-2021 учебный год

МАОУ «СОШ№85» г.Кемерово

Минпросвещения и Рособрнадзор представили проект расписания ОГЭ в 2021 году

Досрочный —  с 20 апреля по 14 мая;

Основной —  с 21 мая по 1 июля;

Дополнительный —  с 3 по 22 сентября.

Основной период

8 июня (вт) 2021

математика

Дополнительный период

6 сентября (пн) 2021

математика

ФИПИ

ПРОЕКТ

Демонстрационный вариант КИМ

Экзаменационная работа состоит из двух частей-

25 заданий.

Часть 1 содержит 19 заданий базового уровня сложности.

Часть 2 содержит 6 заданий с развёрнутым ответом из заданий повышенного и высокого уровней сложности.

На выполнение экзаменационной работы по математике отводится

3 часа 55 минут (235 минут).

Уровень сложности заданий

• Базовый
• Повышенный
• Высокий

ФИПИ

В сравнении с 2019-20 уч.годом в ОГЭ включены практико-ориентированные задания №1-5

В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.

Задание на работу с последовательностями и прогрессиями (задание 12 в КИМ 2020 г.) заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях (задание 14 в КИМ 2021 г.).

Скорректирован порядок заданий в соответствии с тематикой и сложностью.

Информация об изменениях в КИМ ОГЭ 2021

в сравнении с КИМ ОГЭ 2020

МАТЕМАТИКА

Максимальный первичный балл уменьшен с 32 до 31 .

Оценка

5

ПБ

4

22-31

15-21

3

не сдал

8 -14

0-7

Для получения документа об образовании

необходимо набрать 8 первичных баллов, минимум 2 из которых – за выполнение задач по геометрии .

Пояснение к проектам документов, определяющих структуру и содержание КИМ ОГЭ 2021

• В проекте демонстрационного варианта КИМ представлены конкретные примеры заданий, не исчерпывающие всего многообразия возможных формулировок заданий на каждой позиции варианта экзаменационной работы;

• задания не отражают всех вопросов содержания , которые будут проверяться с помощью вариантов КИМ в 2021 г. (полный перечень вопросов, которые могут контролироваться на ОГЭ 2021 г., приведен в спецификации КИМ );

• приведены обязательные для ознакомления инструкции по выполнению работы в целом, ее частей и отдельных заданий, записи ответов;

• приведены критерии оценивания выполнения заданий;

• в проекте спецификации КИМ дано описание экзаменационной работы ;

• приведен обобщенный план варианта КИМ, содержащий полный список тем , задания по которым могут быть представлены на каждой позиции экзаменационного варианта.

Распределение заданий части 1 по разделам содержания курса математики

Название раздела

Количество заданий

1. Числа и вычисления

7

2. Алгебраические выражения

1

3. Уравнения и неравенства

2

4. Числовые последовательности

1

5. Функции и графики

1

6. Координаты на прямой и плоскости

1

7. Геометрия

5

8. Статистика и теория вероятностей

1

Основные умения и способы действий (1 часть)

• Уметь выполнять вычисления и преобразования.
• Уметь выполнять преобразования алгебраических выражений.
• Уметь решать уравнения, неравенства и их системы.
• Уметь строить и читать графики функций.
• Уметь выполнять действия с геометрическими фигурами, координатами и векторами.
• Уметь работать со статистической информацией, находить частоту и вероятность случайного события.
• Уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели.

Распределение заданий части 2 по разделам содержания курса математики

Название раздела

Количество заданий

Уравнения и неравенства

2

Функции и графики

1

Геометрия

3

Уровень сложности заданий

• Базовый – 19 заданий, 19 баллов, максимальное количество
• Повышенный – 4 задания, 8 баллов
• Высокий – 2 задания, 4 балла

ИТОГО – 25 заданий, 31 балл

За часть 1 – 19 баллов

За часть 2 – 12 баллов

За работу

в целом – 31 балл

Правила заполнения бланков ОГЭ 2021

Бланк №1 и №2

Чтобы не потерять баллы на экзамене следует:

• указать правильные ответы,
• правильно заполнять бланки ответов ОГЭ.

При внесении записей в бланки ОГЭ необходимо соблюдать правила заполнения , так как информация, внесенная в бланки, сканируется и обрабатывается с использованием ЭВМ.

Для обработки экзаменационных материалов ОГЭ применяются 3 типа бланков:

Бланк ответов № 1 — предназначен для заданий с кратким ответом.

Бланк ответов № 2 — предназначен для внесения развернутого ответа.

Дополнительный бланк ответов № 2 — при недостатке места для ответов на основном бланке ответов № 2 участник ОГЭ может продолжить записи на дополнительном бланке ответов № 2.

Основные правила заполнения бланков ОГЭ

• Заполняются яркими черными чернилами.
• Пишите по образцу.
• Заполняйте с первой позиции (клетки).
• Каждый символ пишется в одной клетке
• За рамки бланка № 2 нельзя выходить.

Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры , которая соответствует номеру правильного ответа.

Для остальных заданий части 1 ответом является число или последовательность цифр .

Решения заданий

части 2 и ответы к ним запишите на бланке

ответов № 2.

9- 13 ноября 2021 Подготовка к ОГЭ

Задания на урок и д.з.

Интерактивная тетрадь Skysmart

https://edu.skysmart.ru/student/viremisoku

9Б, 9В, 9Г, 9Д

Повторение 9 класс

• Числа и вычисления.
• Алгебраические выражения.
• Уравнения и системы уравнений.
• Неравенства и системы неравенств.
• Последовательности и прогрессии.
• Функции и графики .
• Текстовые задачи.

Тесты в ЭШ

Интерактивная рабочая тетрадь

по алгебре Skysmart

https://edu.skysmart.ru/homework/new

Дискриминант, корни уравнения

Подставить в исходное уравнение

Ответ: -4, -1, 1, 4

или

Ответ: -1; 1; 5

-

(𝑥−1)(𝑥+3)

(𝑥−1)=0

(𝑥+3)=0

Ответ: -1;7

D =64

Практическое задание

РЭШ задания, видеоматериалы

Задание 7 ОГЭ по математике представляет собой задачу на взаимное расположение чисел на числовой (координатной) прямой, их сравнение и оценку.

Какому из данных промежутков принадлежит число 3 / 11 ?

• [0,1; 0,2]
• [0,2; 0,3]
• [0,3; 0,4]
• [0,4; 0,5]

Задание 9 ОГЭ по математике представляет собой несложное рациональное уравнение—линейное или квадратно е либо сводящееся в одно-два действия к одному из них целое или дробно-линейное

уравнение.

Квадратные уравнения представлены в открытом банке ОГЭ по математике всеми типами:

неполные (с нулевым вторым или третьим коэффициентом) и полные (приведённые и неприведённые).

Для того чтобы успешно справиться с подобным заданием на ОГЭ, достаточно:

• уметь решать линейные и квадратные уравнения ,
• помнить правило переноса слагаемого из одной части уравнения в другую (знак этого слагаемого меняется на противоположный),
• обладать определёнными вычислительными навыками , связанными с арифметическими действиями над целыми числами и дробями.

• ЧИСЛА.
• ВИДЫ ЧИСЕЛ.
• ДЕЙСТВИЯ С ЧИСЛАМИ
• ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ

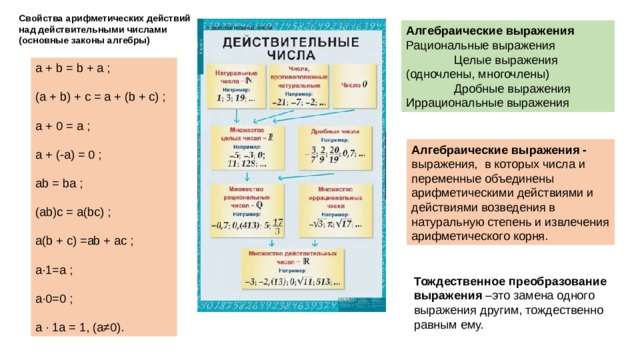
Свойства арифметических действий над действительными числами (основные законы алгебры)

Алгебраические выражения

Рациональные выражения

Целые выражения (одночлены, многочлены)

Дробные выражения

Иррациональные выражения

a + b = b + a ;

( a + b) + c = a + (b + c) ;

a + 0 = a ;

a + (-a) = 0 ;

ab = ba ;

(ab)c = a(bc) ;

a(b + c) =ab + ac ;

a·1=a ;

a·0=0 ;

a · 1a = 1, (a≠0).

Алгебраические выражения - выражения, в которых числа и переменные объединены арифметическими действиями и действиями возведения в натуральную степень и извлечения арифметического корня.

Тождественное преобразование выражения –это замена одного выражения другим, тождественно равным ему.

• Числа и вычисления.
• Алгебраические выражения.
• Уравнения и системы уравнений.
• Неравенства и системы неравенств.
• Последовательности и прогрессии.
• Функции и графики.
• Текстовые задачи.

6 мая

Рациональные выражения. Преобразования рациональных выражений. Повторение.

Российская электронная школа ( РЭШ ), 8 класс, алгебра

Видеоматериалы

Урок 9 Рациональные выражения.

https://resh.edu.ru/subject/lesson/2907/main/

Урок 13 Преобразование рациональных выражений.

https://resh.edu.ru/subject/lesson/1970/main/

Рациональные выражения. Преобразования рациональных выражений. Повторение.

  Рациональное выражение — это любое выражение, составленное из чисел, буквенных переменных, арифметических операций и возведения в степень.  

Все приведенные выражения являются рациональными.

Выражения  в первой строчке являются и рациональными и целыми алгебраическими  выражениями. Они имеют смысл при любых значениях переменных, в отличие от выражений во второй строчке. Например:

теряет смысл при   х = 1   и   х = –1   (делить на нуль нельзя),  

значит, оно рациональное и дробное   (деление на выражение с переменной).     

Упрощение рациональных выражений — это применение  тождественных преобразований, с целью упростить запись выражения  (сделать его короче и удобнее для дальнейшей работы).      Для преобразования рациональных выражений потребуются:

Основное свойство алгебраической дроби.

Правила сложения и вычитания алгебраических дробей.

Правила умножения, деления и возведения в степень алгебраических дробей. и формулы сокращенного умно жения.  

  Основное свойство алгебраической дроби

числитель и знаменатель алгебраической дроби можно умножить на  один и тот же многочлен (в частности, на один и тот же одночлен, на одно  и то же отличное от нуля число);   это   —   тождественное преобразование  заданной алгебраической дроби ;   числитель и знаменатель алгебраической дроби можно разделить   на один и тот же многочлен (в частности, на один и тот же одночлен, на  одно и то же отличное от нуля число);     это   —   тождественное  преобразование заданной алгебраической дроби, его называют   сокращением алгебраической дроби .  

формулы сокращенного умно жения

https://school-assistant.ru/?predmet=algebra&theme=preobrazovanie_raz_virazenij

Задание 6 ОГЭ - задача на арифметические действия с дробями

• Задача на арифметические действия с дробями — как десятичными, так и обыкновенными и комбинациями десятичных и обыкновенных дробей.

• В случае обыкновенных дробей — приведение дробей к общему знаменателю , если знаменатели различны.
• Наиболее простой случай — когда знаменатели одной или двух дробей являются делителями знаменателя другой. В более сложных случаях общий знаменатель находится как произведение знаменателей данных дробей .
• В некоторых случаях бывает удобно выполнить действия, используя распределительные свойства .
• Использовать навыки рационального счёта, например, не выполняя умножение двухзначных или трёхзначных чисел, поскольку на одно из них в конце решения удаётся сократить дробь.
• Рационализировать решение стандартными приёмами: вынесением за скобку общего множителя , применением формул сокращённого умножения, распределительных свойств и т. п.
• Если знаменатели всех дробей в условии являются степенями двойки и пятёрки или произведением таких степеней, дроби лучше обратить в конечные десятичные . Если хотя бы один из знаменателей дробей отличен от степеней двойки и пятёрки или произведения таких степеней, дроби лучше обратить в обыкновенные.

Задание 8

Задачи на действия с целыми степенями и задачи на действия с корнями .