Олимпиадные задания по математике 7 класс
7 класс
7.1. Новогодняя гирлянда, висящая вдоль школьного коридора, состоит из красных и синих лампочек. Рядом с каждой красной лампочкой обязательно есть синяя. Какое наибольшее количество красных лампочек может быть в этой гирлянде, если всего лампочек 50?
7.2. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2, 3, 4, 5, 6, 7, 8 и 9.
7.3. На физическом кружке учитель поставил следующий эксперимент. Он разложил на чашечные весы 16 гирек массами 1, 2, 3, ..., 16 грамм так, что одна из чаш перевесила. Пятнадцать учеников по очереди выходили из класса и забирали с собой по одной гирьке, причем после выхода каждого ученика весы меняли свое положение и перевешивала противоположная чаша весов. Какая гирька могла остаться на весах?
7.4. На клетчатой бумаге нарисован квадрат со стороной 5 клеток. Его требуется разбить на 5 частей одинаковой площади, проводя отрезки внутри квадрата только по линиям сетки. Может ли оказаться так, что суммарная длина проведенных отрезков не превосходит 16 клеток?
7.5. Два парома одновременно отходят от противоположных берегов реки и пересекают её перпендикулярно берегам. Скорости паромов постоянны, но не равны. Паромы встречаются на расстоянии 720 метров от берега, после чего продолжают движение. На обратном пути они встречаются в 400 метрах от другого берега. Какова ширина реки?
Критерии оценивания:
| Баллы | Правильность (ошибочность) решения |
| 7 | Полное верное решение. |
| 6-7 | Верное решение. Имеются небольшие недочеты, в целом не влияющие на решение. |
| 5-6 | Решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений. |
| 4 | Верно рассмотрен один из двух (более сложный) существенных случаев, или в задаче типа «оценка + пример» верно получена оценка. |
| 2-3 | Доказаны вспомогательные утверждения, помогающие в решении задачи. |
| 0-1 | Рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении). |
| 0 | Решение неверное, продвижения отсутствуют. |
| 0 | Решение отсутствует. |
7.1. Новогодняя гирлянда, висящая вдоль школьного коридора, состоит из красных и синих лампочек. Рядом с каждой красной лампочкой обязательно есть синяя. Какое наибольшее количество красных лампочек может быть в этой гирлянде, если всего лампочек 50?
Ответ: 33 лампочки
Решение
Подсчитаем, какое наименьшее количество синих лампочек может быть в гирлянде. Можно считать, что первая лампочка – красная. Поскольку рядом с каждой красной лампочкой обязательно есть синяя, то три красных лампочки не могут идти подряд. Следовательно, среди каждых трех последовательно идущих лампочек хотя бы одна лампочка должна быть синей. Тогда среди первых 48 лампочек синих будет не меньше, чем 48 : 3 = 16. Обе лампочки с номерами 49 и 50 оказаться красными не могут. Итак, синих лампочек в гирлянде должно быть не менее 17. Такой случай возможен: если лампочки с номерами 2, 5, 8, 11, ..., 50 – синие, а остальные – красные, то в гирлянде – 33 красные лампочки.
.
7.2. Найти все двузначные числа, сумма цифр которых не меняется при умножении числа на 2, 3, 4, 5, 6, 7, 8 и 9.
Ответ: 18, 45, 90 и 99.
Решение: По условию сумма цифр числа a и числа 9a одна и та же. Поэтому согласно признаку делимости на 9 число a делится на 9. Двузначные числа, делящиеся на 9, следующие: 18, 27, 36, 45, 54, 63, 72, 81, 90 и 99. Из них числа 27, 36, 54, 63, 72 и 81 не обладают требуемым свойством; в этом можно убедиться, умножая их, соответственно, на 7, 8, 7, 3, 4 и 9. Оставшиеся числа требуемым свойством обладают.
7.3. На физическом кружке учитель поставил следующий эксперимент. Он разложил на чашечные весы 16 гирек массами 1, 2, 3, ..., 16 грамм так, что одна из чаш перевесила. Пятнадцать учеников по очереди выходили из класса и забирали с собой по одной гирьке, причем после выхода каждого ученика весы меняли свое положение и перевешивала противоположная чаша весов. Какая гирька могла остаться на весах?
Ответ
На весах осталась гиря массой 1 грамм.
Решение
Поскольку в каждый момент времени массы на чашах весов отличались хотя бы на 1 грамм, то для того, чтобы перевесила противоположная чаша, необходимо забрать гирю массой не менее двух грамм. Следовательно, выходя из класса, ни один ученик не мог забрать гирю массой 1 грамм.
7.4. На клетчатой бумаге нарисован квадрат со стороной 5 клеток. Его требуется разбить на 5 частей одинаковой площади, проводя отрезки внутри квадрата только по линиям сетки. Может ли оказаться так, что суммарная длина проведенных отрезков не превосходит 16 клеток?
Ответ: да, может
Решение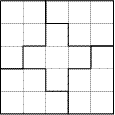
Один из возможных примеров приведен на рисунке (суммарная длина проведенных отрезков равна 16).
7.5. Два парома одновременно отходят от противоположных берегов реки и пересекают её перпендикулярно берегам. Скорости паромов постоянны, но не равны. Паромы встречаются на расстоянии 720 метров от берега, после чего продолжают движение. На обратном пути они встречаются в 400 метрах от другого берега. Какова ширина реки?
Ответ 1760 м
Решение
Суммарное расстояние, пройденное паромами к моменту первой встречи, равно ширине реки, а расстояние, пройденное к моменту второй встречи равно утроенной ширине реки. Следовательно, до второй встречи каждый из паромов прошел втрое большее расстояние, чем до первой встречи. Так как один из паромов до первой встречи прошёл 720 м, то до второй встречи он прошёл расстояние 720·3 = 2160 м. При этом он прошёл путь, равный ширине реки, и ещё 400 м. Следовательно, ширина реки равна 2160 − 400 = 1760 м.


















