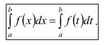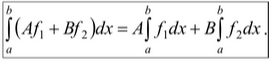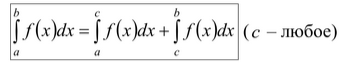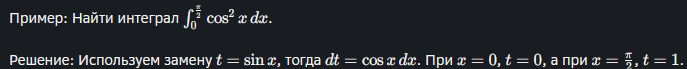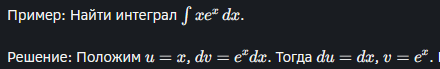МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Хакасский государственный университет им. Н.Ф.
Катанова» (ФГБОУ ВО «ХГУ им. Н.Ф. Катанова»)
Институт естественных наук и математики
Кафедра математики, физики и информационных технологий
Направление подготовки 44.04.01 Педагогическое образование
направленность Современные цифровые технологии в образовании
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Выполнил
Череповская Арина Александровна
Группа СЦТО-21
Курс 2
Форма обучения очная
Абакан, 2024
Оглавление
Введение 3
Магнетики 4
Диамагнетики 5
Парамагнетики 6
Ферромагнетики 7
Магнитный гистерезис 9
Применение ферромагнетиков 11
Контрольные вопросы 15
Список рекомендуемой литературы 15
Введение
Математика занимает центральное место среди наук, предоставляя инструменты и методы для описания и анализа явлений природы, общества и технических систем. Одной из важнейших ветвей математики является математический анализ, который включает в себя такие ключевые понятия, как производные и интегралы. Интегралы играют особую роль в этом разделе, поскольку они находят применение во множестве научных дисциплин, включая физику, инженерию, экономику и биологию.
Определённый интеграл представляет собой фундаментальное понятие в теории интегралов. Он был впервые введен Исааком Ньютоном и Готфридом Вильгельмом Лейбницем в XVII веке, когда они независимо друг от друга разработали основы интегрального исчисления. С тех пор этот инструмент стал неотъемлемой частью математической культуры и нашел многочисленные применения в самых разных областях знаний.
Понятие определенного интеграла
Функция f(x) определена на [a,b].
Рассмотрим разбиение отрезка [a,b] на n отрезков точками
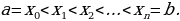
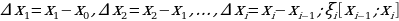 .
.
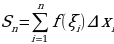 – интегральная сумма функции f(x) на отрезке [a,b].
– интегральная сумма функции f(x) на отрезке [a,b].
Интегральная сумма зависит от способа разбиения [a,b] на отрезки и от способа выбора точки 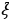 i на отрезке [xi-1,xi].
i на отрезке [xi-1,xi].
Определенным интегралом функции f(x) на [a,b]называется число
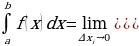
при условии, что предел интегральных сумм существует и не зависит от способа разбиения на элементарные отрезки и от выбора фиксированной
точки 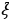 i (a – нижний предел, b – верхний предел определенного интеграла).
i (a – нижний предел, b – верхний предел определенного интеграла).
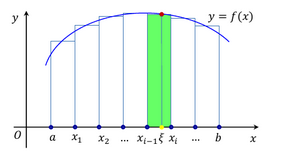
Геометрический смысл определенного интеграла
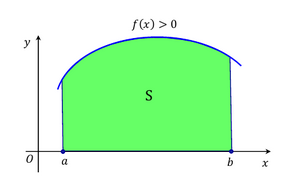
Интеграл 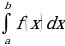 , где f(x)0, численно равен площади S криволинейной трапеции, ограниченной графиком подынтегральной функции, прямыми x=a, x=b и осью Ox.
, где f(x)0, численно равен площади S криволинейной трапеции, ограниченной графиком подынтегральной функции, прямыми x=a, x=b и осью Ox.
Основные свойства определенного интеграла
Свойство 1 (независимость от обозначения переменной)
Величина определенного интеграла не зависит от обозначения переменной интегрирования
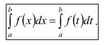
Свойство 2 (линейность)
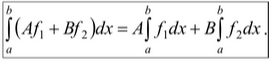
Свойство 3 (аддитивность)
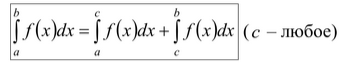
Методы вычисления определённых интегралов
Существует множество методов для вычисления определённых интегралов. Рассмотрим три наиболее распространённых метода.
Метод замены переменных
Метод замены переменных (или подстановки) основан на свойстве замены переменной, описанном выше. Суть метода состоит в том, чтобы заменить переменную интегрирования таким образом, чтобы исходный интеграл преобразовался в более простой для вычисления.
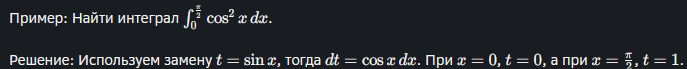
Интегрирование по частям
Метод интегрирования по частям основывается на свойстве интегрирования по частям, представленном ранее. Основная идея метода заключается в выборе одной части подынтегральной функции за u, а другой за dv, так чтобы после применения формулы интегрирования по частям получался более простой интеграл.
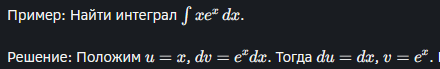
Использование таблиц интегралов
Иногда бывает удобно воспользоваться готовыми результатами, собранными в специальных таблицах интегралов. Эти таблицы содержат стандартные интегралы от различных функций, что позволяет быстро находить решение без необходимости проводить сложные преобразования.
Приложения определенного интеграла
Вычисление площадей фигур. Как уже упоминалось, одно из основных применений определённого интеграла связано с вычислением площадей плоских фигур.
Нахождение объёмов тел вращения. Ещё одно важное применение определённого интеграла связано с нахождением объёмов тел, полученных путём вращения плоской фигуры вокруг некоторой оси.
Работа силы. Определённый интеграл также применяется для вычисления работы силы, если эта сила изменяется вдоль пути перемещения объекта.
Электрическое сопротивление проводника. Определённый интеграл может использоваться для расчёта электрического сопротивления неоднородного проводника.
Среднее значение функции. Среднее значение функции на некотором интервале также может быть найдено с использованием определённого интеграла.
Контрольные вопросы
Что такое определенный интеграл? Как он определяется?
Какие основные свойства определенного интеграла вы знаете?
Опишите метод замены переменных для вычисления определенных интегралов. Приведите пример.
Опишите метод интегрирования по частям. Приведите пример.
Какую роль играют таблицы интегралов в процессе вычисления определенных интегралов?
Как вычислить площадь фигуры, ограниченной графиками двух функций на определенном отрезке?
Как вычисляется объем тела, образованного вращением плоской фигуры вокруг оси абсцисс?
Приведите пример физической задачи, которую можно решить с помощью определенного интеграла.
Чем отличается определенный интеграл от неопределенного интеграла?
Может ли определенный интеграл быть отрицательным? Обоснуйте ответ.
Список рекомендуемой литературы
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Том II. М.: Наука, 1969.
Кудрявцев Л.Д. Курс математического анализа. Том I. М.: Высшая школа, 1988.
Демидович Б.П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1977.
Ильин В.А., Позняк Э.Г. Основы математического анализа. Часть II. М.: Физматлит, 2002.
Зорич В.А. Математический анализ. Том I. М.: МЦНМО, 2012.
Виноградова И.А., Олехник С.Н., Садовничий В.А. Задачи и упражнения по математическому анализу. Часть II. М.: МГУ, 1993.
Никольский С.М. Курс математического анализа. Том I. М.: Наука, 1983.
Шилов Г.Е. Математический анализ. Функции одного переменного. Часть III. М.: Наука, 1970.
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 1989.
Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М.: Дрофа, 2005.







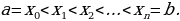
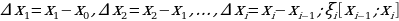 .
.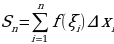 – интегральная сумма функции f(x) на отрезке [a,b].
– интегральная сумма функции f(x) на отрезке [a,b].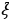 i на отрезке [xi-1,xi].
i на отрезке [xi-1,xi].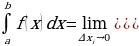
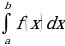 , где f(x)0, численно равен площади S криволинейной трапеции, ограниченной графиком подынтегральной функции, прямыми x=a, x=b и осью Ox.
, где f(x)0, численно равен площади S криволинейной трапеции, ограниченной графиком подынтегральной функции, прямыми x=a, x=b и осью Ox.