Определение значений коэффициентов квадратичной функции по графику.

Определение значений коэффициентов квадратичной функции по графику.

Методическая разработка Сагнаевой А.М.

МБОУ СОШ№44 г. Сургут, ХМАО-Югра .

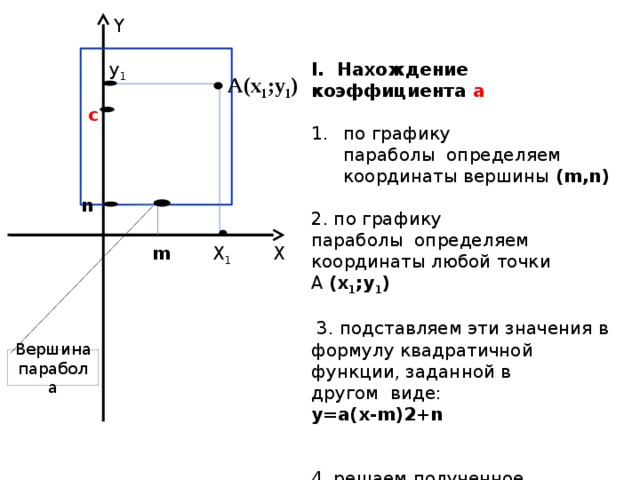
Y

у 1

Ι. Нахождение коэффициента а

• по графику параболы  определяем координаты вершины  (m,n)

2. по графику параболы  определяем координаты любой точки А  (х 1 ;у 1 )

3. подставляем эти значения в формулу квадратичной функции, заданной в другом  виде:

у=a(х-m)2+n

4. решаем полученное уравнение.

А(х 1 ;у 1 )

c

n

Х

m

Х 1

Вершина

парабола

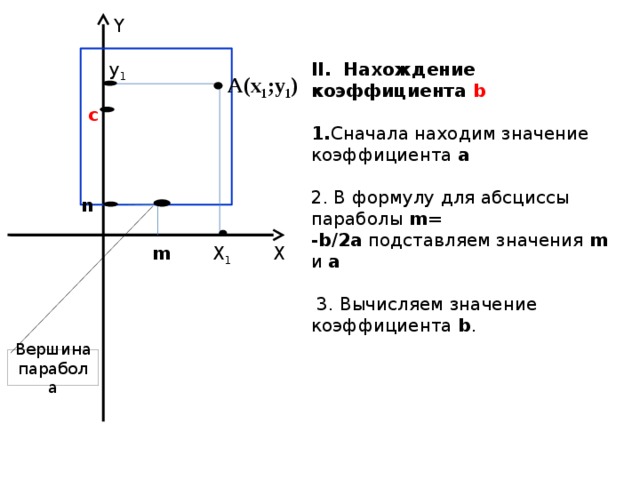
Y

ΙΙ. Нахождение коэффициента b

у 1

1. Сначала находим значение коэффициента  a

2. В формулу для абсциссы параболы  m= -b/2a  подставляем значения  m и a

3. Вычисляем значение коэффициента  b .

А(х 1 ;у 1 )

c

n

Х

Х 1

m

Вершина

парабола

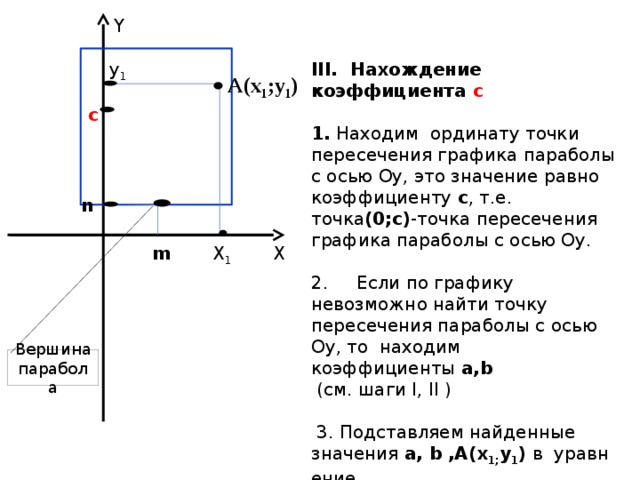
Y

ΙΙΙ. Нахождение коэффициента c

у 1

1. Находим ординату точки пересечения графика параболы с осью Оу, это значение равно коэффициенту  с , т.е. точка (0;с) -точка пересечения графика параболы с осью Оу.

2.     Если по графику невозможно найти точку пересечения параболы с осью Оу, то находим коэффициенты  a,b

(см. шаги Ι, ΙΙ )

3. Подставляем найденные значения  a, b ,А(х 1; у 1 )  в  уравнение

  у=ax 2  +bx+c  и находим  с.

А(х 1 ;у 1 )

c

n

Х

Х 1

m

Вершина

парабола

Задачи

1

2

4

3

5

6

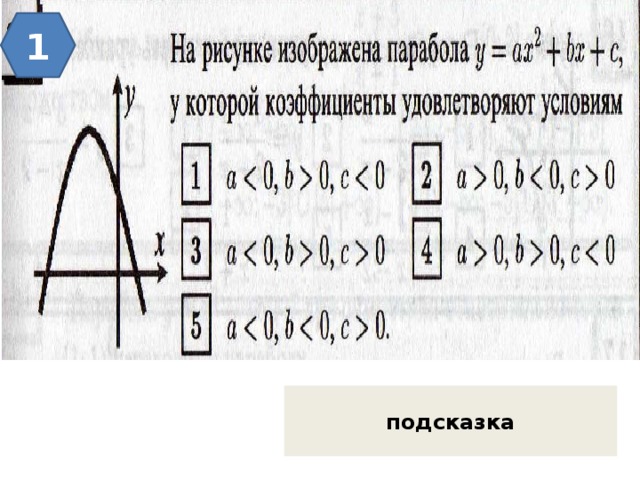
1

подсказка

Ιх 2 Ι , а х 1 0, т.к. a Ордината точки пересечения параболы с осью ОY – коэффициент с Ответ: 5 с х 1 х 2 " width="640"

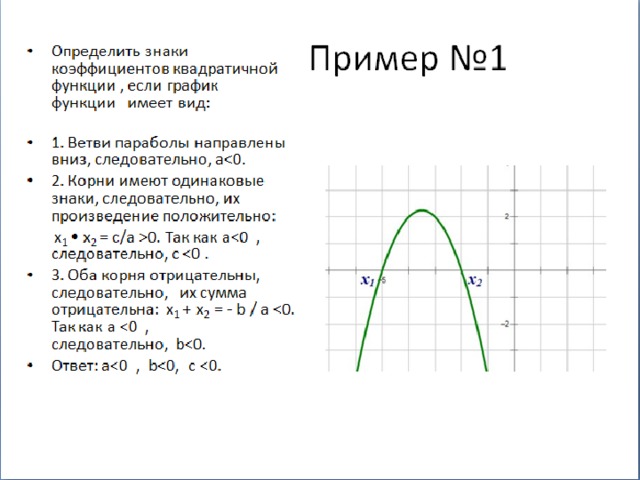
• Ветви параболы направлены вниз,

значит а

• Корни имеют разные знаки,Ι х 1 ΙΙх 2 Ι , а х 1 0, т.к. a
• Ордината точки пересечения параболы с осью ОY – коэффициент с

Ответ: 5

с

х 1

х 2

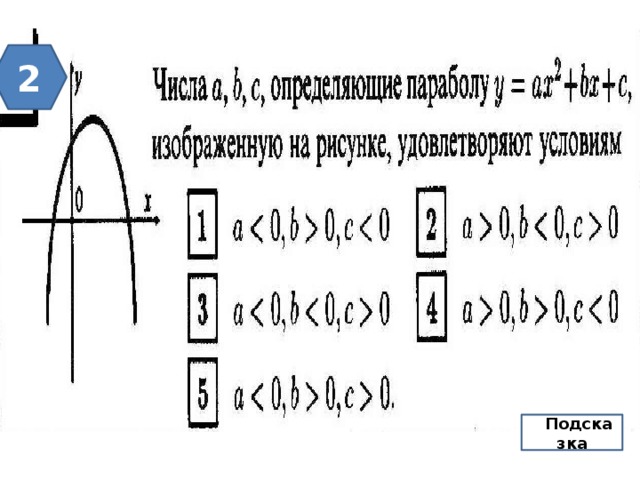
2

П Подсказка

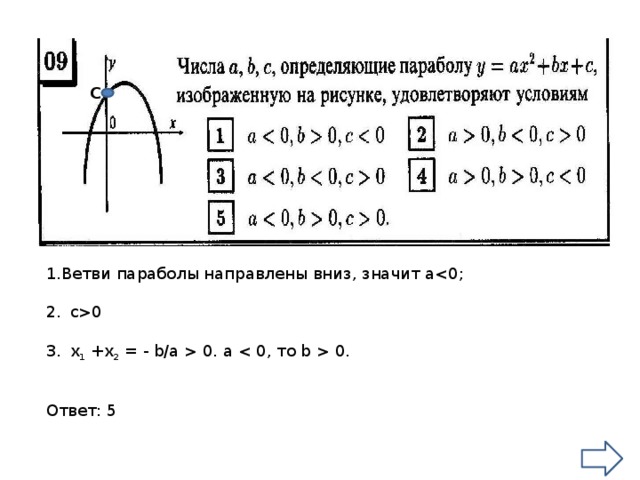0 x 1 +x 2 = - b/a 0. a 0. Ответ: 5 " width="640"

C

1.Ветви параболы направлены вниз, значит а

• с0

• x 1 +x 2 = - b/a 0. a 0.

Ответ: 5

0 , т.к. ветви параболы направлены вверх; 2. с=у(0)3. Вершина параболы имеет положительную абсциссу: при этом а 0, следовательно, b4. D0, т.к. парабола пересекает ось ОХ в двух различных точках. " width="640"

3

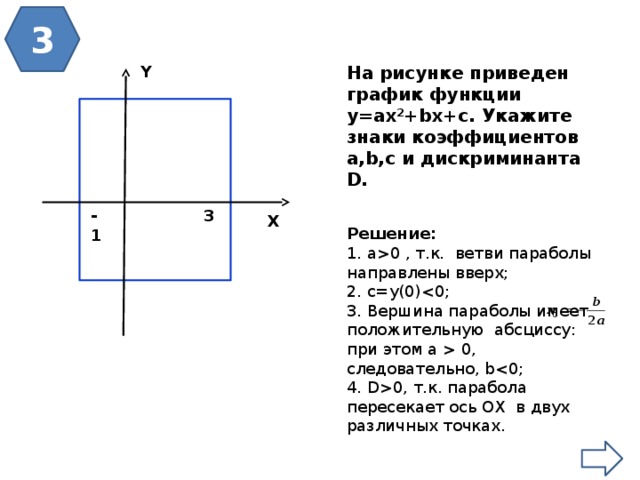
Y

На рисунке приведен график функции у=ax 2 +bx+c. Укажите знаки коэффициентов a,b,c и дискриминанта D.

-1

3

X

Решение:

1. а0 , т.к. ветви параболы направлены вверх;

2. с=у(0)

3. Вершина параболы имеет положительную абсциссу:

при этом а 0, следовательно, b

4. D0, т.к. парабола пересекает ось ОХ в двух различных точках.

4

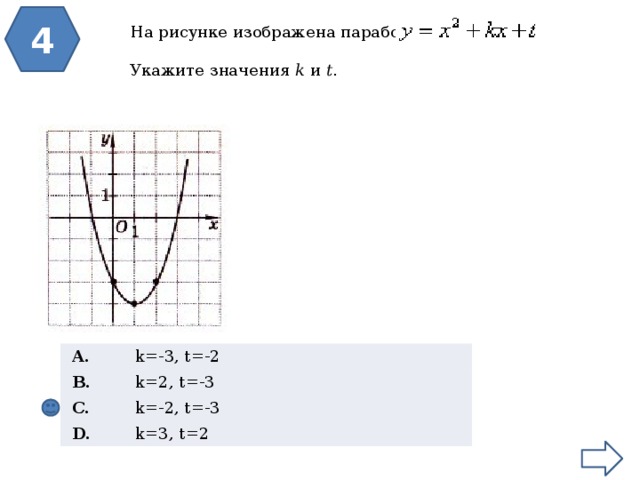
На рисунке изображена парабола

Укажите значения  k  и  t .

  A.

  B.

k=-3, t=-2

  C.

k=2, t=-3

k=-2, t=-3

  D.

k=3, t=2

5

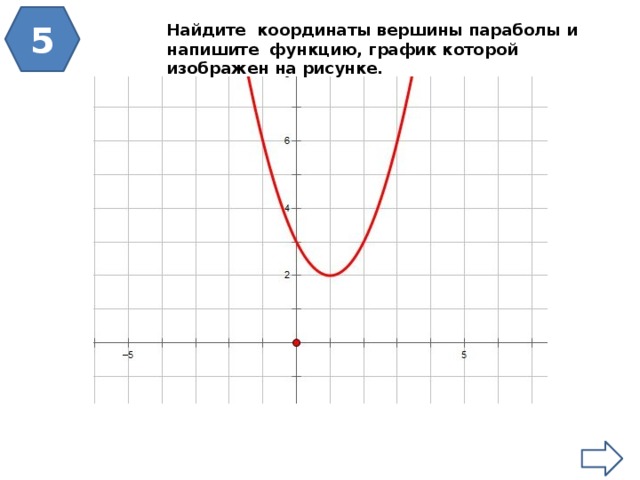
Найдите координаты вершины параболы и напишите функцию, график которой изображен на рисунке.

6

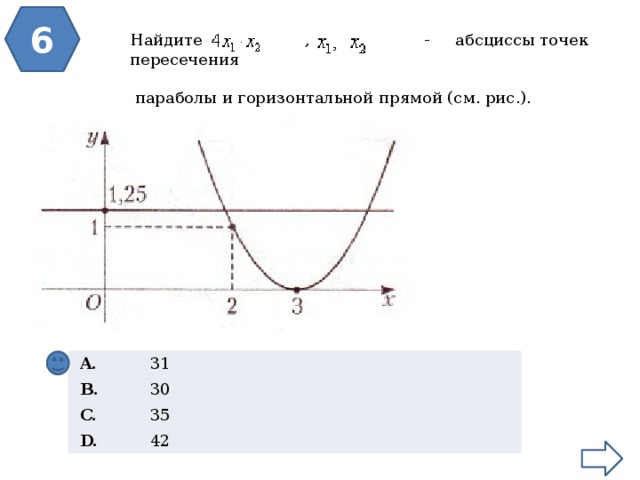
Найдите  , где    - абсциссы точек пересечения

параболы и горизонтальной прямой (см. рис.).

  A.

  B.

31

  C.

30

35

  D.

42