Основные понятия графов

Занятие 23. Основные понятия и определения графа и его элементов

План лекции:

1. Понятие графа

2. Виды графов

3. Основные понятия элементов графа

Понятие графа

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.

Рассмотрим задачу.

Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Вене; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса ?

Решение: Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Теперь сразу видно, что долететь с Земли до Марса нельзя.

Решение этой двух задачи – графическое представление. Она состоит из несколько точек, некоторые из которых соединены линиями. Такие картинки и называются графами. Точки при этом называются вершинами, а линии – ребрами графа.

Графом G(V,X) называется пара двух конечных множеств: множества точек и множества линий, соединяющих некоторые пары точек. Точки называются вершинами графа и обозначаются А,В,С и т.д., линии – ребрами графа и обозначаются а,в,с, х1,х2,х3 и т.д.

Виды графов

Если в графе все ребра не имеют порядка (то есть ребра не имеют стрелок), то граф называется неориентированным.

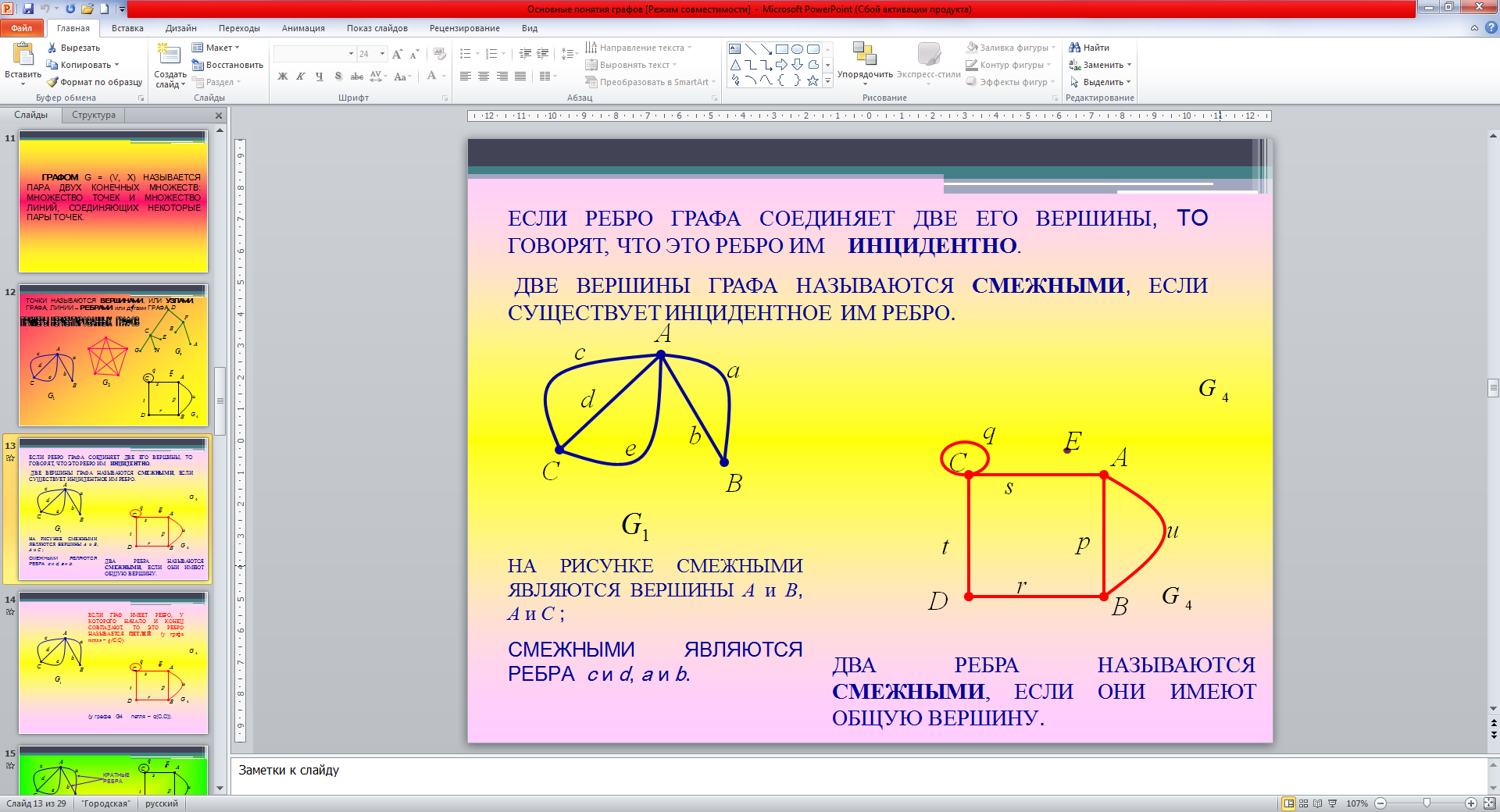
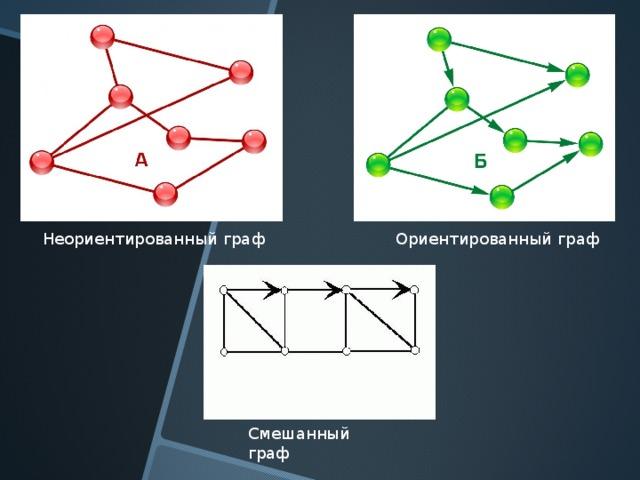
Рисунок 1 – Неориентированные графы

Если все ребра в графе являются упорядоченными (то есть ребра имеют стрелки), то граф называется ориентированным. В нем ребра называются дугами.

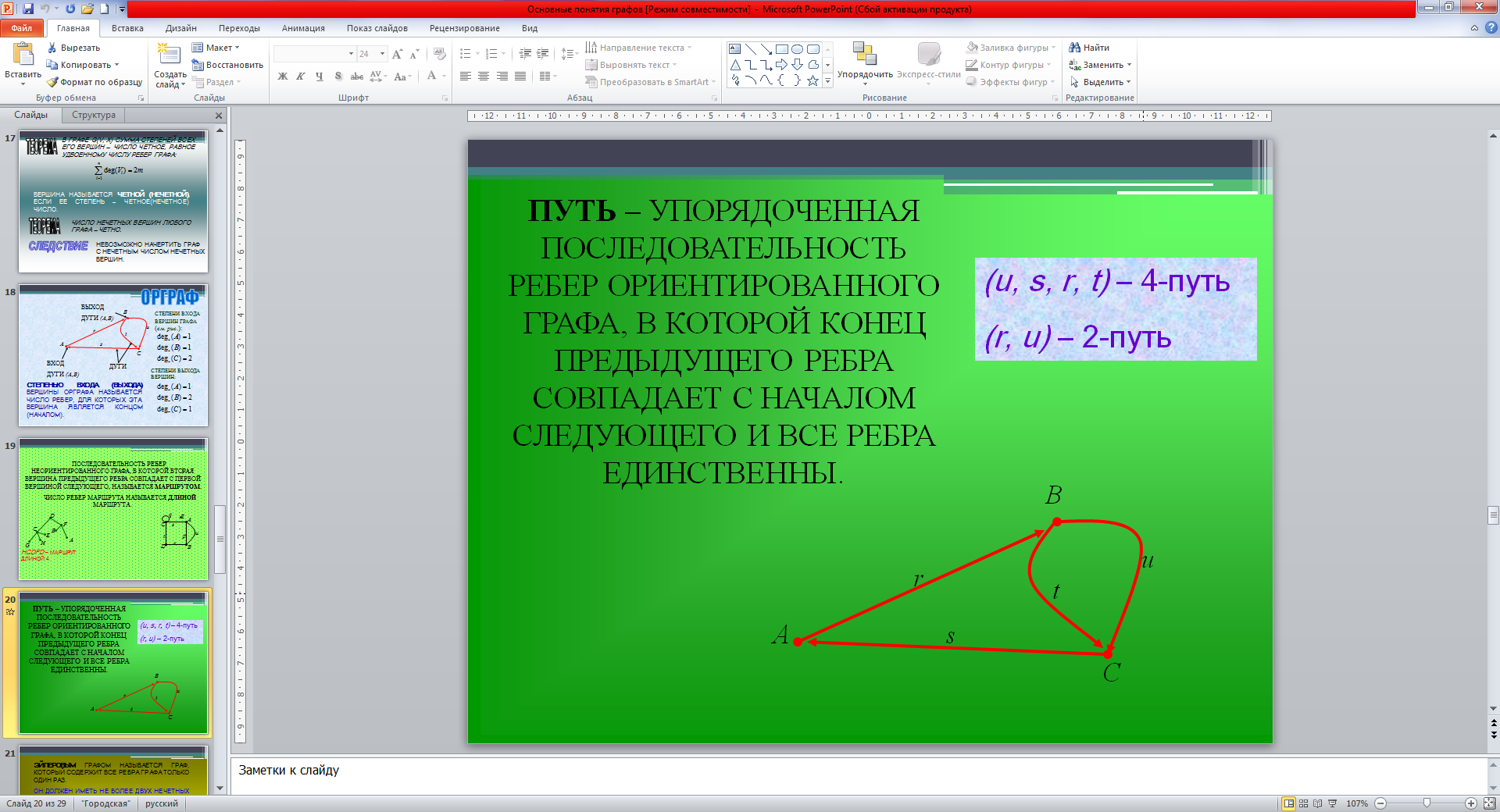
Рисунок 2 – Ориентированные графы

Дуга у ориентированного графа, как у вектора, имеет направление, то есть имеет начало и конец. Начало (где нет стрелки) называют выходом, конец (где есть стрелка) – входом. Это важные понятия.

Если в графе имеются и ребра и дуги (то есть и со стрелками и без стрелок), то граф называется смешанным.

Рисунок 3 – Смешанный граф

Легко найти примеры графов в самых разных областях науки и практики. Сеть дорог, трубопроводов, электрическая цепь, структурная формула химического соединения, блок-схема программы и др.

Основные понятия элементов графа

Рассмотрим основные понятия элементов графов. Эти понятия могут называться одинаково, но немного по-разному определятся в каждом виде графа. А в смешанном графе будут определяться двояко, как для ориентированного графа, так и для неориентированного. Чтобы рассмотреть подробнее все понятия, нарисуйте в тетради четыре графа – рис.1, рис.2, рис.4, рис.5

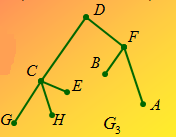
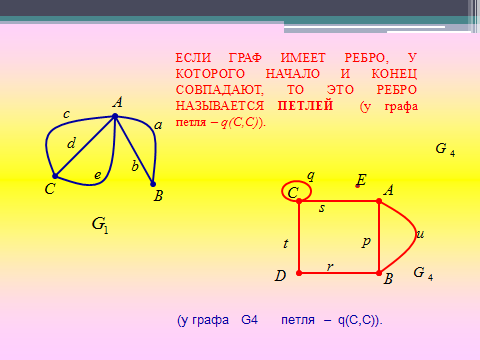
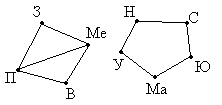
Рисунок 4 Рисунок 5

1. Инцидентность. Если ребро или дуга графа соединяет две его вершины, то говорят, что это ребро им инцидентно. Например, на рис.1 ребро r инцидентно вершинам D и B (так как соединяет их). На рис. 2 дуга s инцидентно вершинам C и A. На рис. 5 ребро а инцидентно вершинам А и В.

2. Смежность. Это понятие распространяется как на ребра и дуги, так и на вершины. Рассмотрим их подробнее.

Две вершины графа называются смежными, если существует инцидентное им ребро или дуга. Например, рис.1 смежные вершины – С и А, С и D, А и В, А и D; рис.2 смежные вершины – А и В, А и С, В и С.

Для неориентированного графа: два ребра называются смежными, если они имеют общую вершину. Например, рис.5 смежные ребра – c и d и e, a и b

Для ориентированного графа: две дуги называются смежными, если они имеют общих выход. Например, рис.2 смежные дуги – t и u

1. Петля. Ребро, у которого начало и конец совпадают, называют петлей и обозначается, например q(С,С), как в графе на рис.1 Петли могут быть и в ориентированном графе, как на следующем рисунке а(1,1) и с(2,2)

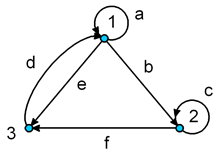
1. Кратность. Это понятие для каждого вида графа определятся немного по-разному.

Для неориентированного графа: ребра, имеющие одинаковые концы, называются кратными, например рис.1 кратные ребра - p и u; рис.5 кратные ребра - c и d и e, a и b.

Для ориентированного графа: дуги называются кратными, если они имеют одинаковые начальные и конечные вершины, т.е. имеют одинаковое направление, например, рис.2 кратные дуги - t(B,C) и u(B,C).

1. Степень вершин. Это понятие для каждого вида графа определятся немного по-разному.

Для неориентированного графа: число ребер, инцидентных одной вершине, называется степенью этой вершины и обозначается deg. Другими словами – количество ребер выходящих из одной и той же вершины будет считаться степенью этой вершины. Например, рис.1 степень вершины А записывается как deg(A)=3 (т.к. из А выходят 3 ребра), deg(D)=2. Для рис.5 deg(A)=5. Если в вершине петля, то она дает вклад в степень, равный 2 (т.к. ребро и выходит и входит в эту вершину), т.е. на рис.1 deg(С)=4.

Для ориентированного графа: находят полустепени входа и выхода дуг. Степень входа – это число дуг, для которых эта вершина является концом, т.е. на рис.2 deg₊(A)=1 (+ - это вход дуги).

Степень выхода – это число дуг, для которых эта вершина является началом, т.е.рис.2 deg _(A)=1(- - это вход дуги). Пример, рис.2 deg₊(В)=1 deg _(В)=2; deg₊(С)=2 deg _(С)=1.

1. Изолированная вершина. Вершина графа, имеющая степень, равную 0, называется изолированной. То есть, это та вершина, которая не соединяется ни с одним ребром или дугой. Например, рис.1 изолированная вершина – Е.

2. Висячая вершина. Вершина графа, имеющая степень равную 1, называется висячей. То есть, это та вершина, которая соединяется только с одним ребром или дугой. Например, рис.4 висячие вершины – Q, H, E, B, A.

3. Четность и нечетность вершин. Вершина называется четной (нечетной), если её степень – четное (нечетное) число. Например, рис.1 четные вершины – D и C (т.к. deg(D)=2 и deg(С)=4), нечетные вершины – А и В (т.к. deg(A)=3 и deg(В)=3).

4. Маршрут. Это понятие распространяется только на неориентированный граф.

Маршрут – это последовательность попарно инцидентных вершин неориентированного графа. То есть, это ряд вершин, которые соединяются ребрами и по ним можно пройти от начальной вершины к конечной. Например, рис.1 маршруты – ВАВDCCA, DВА; рис.4 маршрут – FDCH. Длина маршрута определяется количеством пройденных ребер, например, длина маршрута DВА=2, длина маршрута FDCH=3.

1. Путь. Это понятие распространяется только на ориентированный граф.

Путь – это упорядоченная последовательность дуг ориентированного графа, в которой конец предыдущей дуги совпадает с началом следующей и все дуги единственны. То есть, нельзя проходить дважды по одной и той же дуге. Например, рис.2 пути – rus, tsru. Длина пути определяется количеством дуг, то есть рис.2 длина пути rus=3, длина пути tsru=4.

1. Гамильтонов путь. Гамильтоновым путем графа называется путь, проходящий через каждую его вершину только один раз. Например, рис2 гамильтонов путь – ru или ts.

2. Эйлеров граф. Эйлеровым графом называется граф, который содержит все ребра графа только один раз. Он должен иметь не более двух нечетных вершин.

3. Теорема: В графе G(V, X) сумма степеней всех его вершин – число четное. Число нечетных вершин любого графа – четно. Невозможно начертить граф с нечетным числом нечетных вершин.

Самостоятельная работа студентов

1. Переписать лекцию в тетрадь и прислать фото

2. Разобрать каждое понятие на примерах до понимания

3. Определить по рис.4

   1. степени вершин С, F, H

   2. смежность всех вершин и смежность любых трех ребер

   3. инцидентность ребер и вершин (3 примера)

   4. определить, является ли этот граф Эйлеровым

4. Определить для следующего ориентированного графа следующие понятия

1. Кратные дуги

2. Петли

3. Путь длины 5

4. Полустепени всех вершин