XXVII Республиканская научная конференция молодых исследователей
«Шаг в будущее»
Исследовательская работа:
«Основные виды и способы решения текстовых задач на ОГЭ по математике»
Симпозиум: Математика и информационные технологии
Направление: Прикладная математика.
Выполнила: Мидетова Айшат Сурхаевна
ученица 9-б класса МКОУ «Самурская СОШ»
Адрес: с. Самур, ул.Родниковая 4, Магарамкентского района РД
Научный руководитель :Рамазанова Эмма Джаруллаевна
учитель математики Самурской СОШ
Адрес: с. Самур, ул.Пушкина 18,Магарамкентского района РД
Телефон 8 963 424 55 14
2021 год
Аннотация
В данной работе ведется исследование и решение текстовых задач, которые можно встретить в школьном курсе математики, а также в контрольно- измерительных материалах ОГЭ и ЕГЭ . Работа состоит из введения, двух глав , заключения и литературы. В первой главе приведены примеры основных видов текстовых задач. Вторая глава состоит из двух пунктов. В первом пункте представлены основные способы решения текстовых задач, которые встречаются в школьном курсе, а во втором пункте приведены примеры текстовых задач и их решение из вариантов ОГЭ последних лет. Все текстовые задачи, приведенные в работе, решены составлением таблиц и схем.
Тема актуальна, так как текстовые задачи есть в вариантах ГИА, но в школьном курсе математики не достаточно изучаются все виды и способы их решения.
Цель данной работы более глубокое изучение этой темы, выявление наиболее рационального решения, которое быстро приводит к ответу.
Работа может служить методическим материалом для факультативного курса в 9-11 классах.
Введение
С давних пор задачи играют огромную роль в обучении. В школьном курсе математики отводится немалое количество часов решению задач. Но тем не менее у многих моих одноклассников возникают трудности при решении текстовых задач. Это и не удивительно, поскольку у большинства учащихся нет должной подготовки для решения текстовых задач. При решении задач у нас развивается внимание, наблюдательность, логическое мышление, речь, сообразительность. В процессе решения задач у нас развиваются способности не только математические, но и общие, интеллектуальные, которые, в свою очередь, необходимы для развития нас в целом, способствуя нашей успеваемости почти по всем школьным предметам. Поэтому я поставила перед собой задачу изучить данную тему, попробовать научиться решать текстовые задачи и разработать способы решения задач и набор рекомендаций в помощь выпускникам для получения высоких баллов на ОГЭ.
Актуальность данной темы определяется необходимостью уметь решать задачи в школе и при сдаче ОГЭ.
Цель данной работы -более глубокое изучение этой темы, выявление наиболее рационального решения .приводящее к быстрому ответу.
Для достижения цели нужно решить следующие задачи:
- Изучить литературу об основных видах математических задач.
- Познакомиться с методами решения текстовых задач, предложенными в школьном курсе и предложить их решение с помощью таблиц и схем.
- Рассмотреть решения текстовых задач в контрольно-измерительных материалах ОГЭ .
. Объектом исследования были текстовые задачи школьного курса и КИМ ОГЭ.
Структура данной работы включает в себя теорию, практическую часть, список литературы.
Я надеюсь, что знания ,полученные мной в процессе работы ,помогут мне и многим выпускникам при сдаче ОГЭ и при поступлении в ВУЗ.
Глава 1. Основные виды задач.
Если говорить об основных видах задач, то необходимо для начала определить, из каких компонентов они состоят и на какие этапы можно разделить процесс решения задачи.
В методике преподавания математике процесс решения текстовых задач делят на четыре этапа:
1)Понимание условия задачи.
Это самый главный этап в решении задачи, так как учащиеся должны понимать, что дано в условии и что требуется найти в задаче. Они должны осмыслить отдельные элементы условия, после этого они производят поиск необходимой информации в своей памяти, и сопоставить с известной информацией условие и заключение задачи.
2) Составление плана решения.
Учащимся необходимо разработать целенаправленные действия всевозможных сочетаний из данных и искомых, довести задачу к известному типу, выбрать для решения самый оптимальный метод и наметить для себя план решения.
3)Реализация плана решения.
В этом этапе учащиеся почти выполняют план решения, выбирают подходящий способ для оформления решения и оформляют его.
4) Исследование найденного решения.
Учащиеся делают акцент на конечном результате решения задачи, анализируют его, по необходимости проводят исследование особых и частных случаев
Если рассматривать, как задачи относятся к теории то можно выделить стандартные и нестандартные задачи.
Рассмотрим на примере стандартные задачи:
1. Первый мотоциклист за 3часа проехал на 36км больше, чем второй за 2час. Найдите скорость каждого, если скорость второго мотоциклиста на 25 км/ч меньше скорости первого.
2. В классе 36 учеников. По математике за четверть отметку «5» имеют 8 человек, отметку «4» – 12 человек, а остальные – отметку «3». Постройте круговую диаграмму. По этим данным построить круговую диаграмму.
Рассмотрим на примере нестандартные задачи:
Александр, Борис, Виктор и Григорий – друзья. Один из них врач, другой – журналист, третий – спортсмен, а четвертый – строитель. Журналист написал статью об Александре и Григории. Спортсмен и журналист вместе с Борисом ходили в поход. Александр и Борис были на приеме у врача. У кого какая профессия?
По своему математическому содержанию, соответствующей специфике той или другой математической дисциплины, задачи можно разделить на: алгебраические, арифметические, геометрические, аналитические.
По содержанию задачи группируют на:
задачи на движение,
задачи на проценты и сложные проценты,
внутри каждого образа в зависимости от логической структуры задачи разделяют еще следующие виды задач:
задачи на совместную работу,
задачи на концентрацию ,сплавы и смеси.
По характеру различают следующий вид задач:
1)На вычисление.
2)На построение.
3)На доказательство
4)На исследование.
5)На моделирование.
6)текстовые задачи.
7)задачи комбинированного характера.
Глава2. Решение текстовых задач.
1.Решение текстовых задач в школьном курсе математики.
В школьном курсе математики решение текстовых задач облегчит, если составить к ним схемы или таблицы. Я в данной работе хочу привести решение некоторых текстовых задач из школьного курса математики, а также из контрольно измерительных материалов ОГЭ, составлением краткой записи в виде таблиц или рисунка. В школьных учебниках эти задачи решены составлением уравнения или системы уравнений. С этой задачей не все учащиеся справляются. А если к задачам составить таблицу или схему ,то уравнение к ним легко составить
Краткие записи условия задачи в виде таблиц, рисунков, графиков, диаграмм и т.д., дают возможность одновременно видеть все связи между данными.
Схема краткой записи в виде таблицы:
Прочитав задачу, необходимо ответить на вопросы, постепенно оформляя на черновике краткое условие в виде таблицы:
Какими величинами характеризуется процесс в данной задаче?
Сколько процессов в задаче?
Какие величины известны, и что нужно найти? (Таблица заполняется данными задачи и ставится знак вопроса против той величины, которую надо найти)
Как связаны величины в задаче, какими формулами?
Обозначаем неизвестную величину за Х .
Какое условие нужно использовать для составления уравнения?
Легко ли решать полученное уравнение?
Рассмотрим пример составления такой краткой записи:
Проиллюстрируем это на примере следующих задач 6 кл. Тема: Прямая и обратная пропорциональности.
Задача1.Стальной шарик объемом 6 см^3 массу 46,8г.Какова масса шарика из той же стали, если его объем 2,5см^3?
|
| Объем,см^3 | Масса, г | Величины: Прямо пропорц. |
| Стальной шарик | 6 | ↓ | 46,8 ↓ |
| Стальной шарик | 2,5 | ↓ | х ↓ |
После составления таблицы очень легко составить пропорцию и решить задачу.
6:2,5=46,8:х
Х=46,8х2,5:6=19,5(г).
Ответ.19,5 г.
Задача 2. Для строительства стадиона 5 бульдозеров расчистили площадку за 200 мин.За какое время 8 бульдозеров расчистили бы эту площадку?
|
| Число бульдозеров | Время расчистки(мин) | Величины: Обр.пропорц.
|
| площадка | 5 | ↑ | 200 ↓ |
| площадка | 8 | ↑ | Х ↓ |
Составим пропорцию для обратно пропорциональных величин.
5:8=Х:200
Х=5х200:8=125(мин)
Ответ.125 мин.
Схема краткой записи в виде рисунка
Очень часто в задаче на нахождение реальных неизвестных используются понятия из геометрии: площадь, периметр, прямоугольник.
Задача 3. Площадь участка, имеющий форму прямоугольника, равна 210 кв.м., а периметр равен 62 м.Найдите стороны участка.
Х м
У,м
| Длина,м | Ширина,м | Площадь,кв.м | Периметр,м |
| х | у | ху=210 | 2х+2у=62 |
С помощью таблицы составим два уравнения с двумя переменными:
Из уравнения 2х+2у=62 получим х+у=31 откуда х=31-у, подставив в первое уравнение вместо х получим (31-у)у=210.Получили квадратное уравнение, решив которого можно получить решение задачи.
у=10 и у=21, а х=21 и х=10.
Ответ.21м и 10м или 10м и 21м.
Рассмотрим еще одну задачу ,где используется прямоугольный треугольник.
Задача 4. Периметр прямоугольного треугольника равен 84см,а его гипотенуза равна 37.Найдите площадь треугольника.
.
Х см
ууу У см
| Стороны прямоугольного треугольника | Площадь, S | Периметр,P |
| х | у | 37см | 1/2ху | 84см |
Пользуясь данными таблицы, составим уравнения для периметра и теоремы Пифагора.
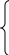
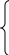
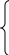 х+у +37=84 х=47-у х1= 12,х2=35
х+у +37=84 х=47-у х1= 12,х2=35
x^2 + y^2=37^2 , (47-у)^2+y^2=1369, у1=35, у2=12
Решая систему уравнений ,можно найти катеты прямоугольного треугольника, а затем и площадь S=(12х35):2=210(см^2).
Ответ.210кв.см.
Рассмотрим стандартные задачи, которые можно решить не только с конкретными числами, но и в общем виде. Это позволит решить целый класс однотипных задач, отличающихся лишь числовыми значениями..
Задача 5. Через первую трубу бассейн наполняется за 20 ч, через вторую – за 30 ч. За сколько часов бассейн наполнится через обе эти трубы?
1) Обычно объём работы принимают за единицу. В задачах с бассейнами и трубами объём бассейна принимают за единицу. Но можно также обозначить любой буквой (произвольной постоянной).
2) Производительность работы - это количество работы, выполненной за единицу времени.
|
| 1 труба | 2 труба | Обе трубы |
| Производительность, л/мин | V/20 | V/30 | V/х |
| Объем, л | V | V | V |
| Время, мин | 20 | 30 | х? |
Составим уравнение по таблице V/20+V/30=V/x или 1/20 +1/30 =1/x.решив это уравнение ,получим 5/60=1/x ,откуда x=12(ч.)
Ответ.12ч.
2. Примеры решения текстовых задач из
контрольно- измерительных материалов ОГЭ.
Решение задач с помощью уравнения, т.е. перенос данных задачи на математический язык с использованием замены неизвестных в задаче переменными называется моделированием. В краткой записи необходимо пояснять, какой переменной выражается определенный процесс задачи, а также указывать при каких значениях эта переменная имеет смысл. Кроме этого, делаются дополнительные записи соответствующих формул, на основании которых связываются величины в задаче.
Необходимо проверить корни уравнения к условиям задачи, выявив посторонние корни.
Записать полный ответ на поставленный вопрос задачи.
Задачи на движение.
Задачи на движение, как правило представляют собой задачи с использованием объектов, совершающих какое-либо действие. Это могут быть пешеходы, велосипедисты, автомобили, лодки и так далее. Существует 3 вида задач на движение: движение двух объектов навстречу друг другу, движение в противоположных и обратных направлениях, движение из одной точки в одном направлении. Доминирующими понятиями в таких задачах являются скорость(V), время(t) и расстояние(S) и формула, связывающая эти понятия:
S = V * t.
Задача.1Моторная лодка прошла против течения реки 55 км и вернулась в пункт отправления, затратив на обратный путь на 6 часов меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 8 км/ч. Ответ дайте в км/ч.
|
| По течению реки | Против течения реки |
| Скорость,v | (8+х)км/ч | (8-х)км/ч |
| Путь,s | 55км | 55км |
| Время,t | 55/8+x,ч на 6ч | 55/8-x,ч |
Составим уравнение для задачи.
55/8-x -55/8+x=6
Решая уравнение ,получим корни Х1=3, Х2=-64/3( не удовлетворяет условию задачи).
Ответ.3км/ч.
Задача 2. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 28 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 286 км, скорость первого велосипедиста равна 10 км/ч, скорость второго — 30 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.
|
| Расстояние до встречи,км | Время,ч | Скорость,км/ч |
| 1велосипедист | 286-х | 286-х/10 +28/60 | 10 |
| 2 велосипедист | x ? | x/30 | 30 |
Решение.
Обозначим через x км – расстояние от города, из которого выехал второй велосипедист, до точки встречи. Тогда первый велосипедист проехал 286-x км. Время, которое потратил второй велосипедист в пути, составило 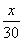 часов, а первого – 286-x/10+28/60 часа. Так как оба велосипедиста выехали одновременно навстречу друг другу, то к моменту их встречи они находились в пути одинаковое время. Имеем уравнение:
часов, а первого – 286-x/10+28/60 часа. Так как оба велосипедиста выехали одновременно навстречу друг другу, то к моменту их встречи они находились в пути одинаковое время. Имеем уравнение:
x/30=286-x/10+28/60.
Упрощаем, находим x, получаем: x=218
Ответ.218 км.
Большое количество задач – смешивание товаров разной цены, жидкостей с различным содержанием соли, кислот разной концентрации, сплавление металлов с различным содержанием некоторого компонента – можно рассмотреть в общем виде.
Задачи на смеси и сплавы.
Задача 3 . В сосуд ,содержащий 5 литров 27-процентного водного раствора вещества ,добавили 4 литра воды. Сколько процентов составляет концентрация получившегося раствора?
|
| Концентрация вещества в растворе,% | Масса раствора, л | Масса вещества в растворе, л |
| 1раствор | 27 | 5 | 0,27х5=1,35 |
| 2 раствор | 0 | 4 | 0 |
| Смесь | Х | 9 | 1,35 |
Составляем уравнение 9- 100%
1,35- Х% откуда Х=1,35х100:9=15(%)
Ответ.15%
Задача 4. Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60 % кислоты. Сколько килограммов кислоты содержится во втором растворе?
1случай
|
| Весь раствор, кг | Концентрация кислоты ,% | Масса кислоты, кг |
| 1раствор | 12 | Х | 12Х |
| 2 раствор | 8 | У | 8У |
| смесь | 20 | 65 | 0,65х20 |
2 случай
|
| Весь раствор, кг | Концентрация кислоты, % | Масса кислоты, кг |
| 1раствор | 1 | Х | 1Х |
| 2 раствор | 1 | У | 1У |
| смесь | 2 | 60 | 0,6х2 |
Решение.
Пусть x% - концентрация первого раствора и y% - концентрация второго раствора. По первой таблице получим следующее уравнение
12Х+8У=0,65х20
Также в задаче сказано, что при равных объемах растворов получается раствор 60% кислоты, то есть по второй таблице можно записать следующее уравнение1Х+1У=0,6х2
Получаем систему двух уравнений:
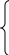
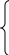
12Х+8У=0,65х20 Х=1,2-У У=0,35,откуда Х= 0,35х8=2,8
1Х+1У=0,6х2 12(1,2-У)+8У=13
Ответ.2,8кг
Задачи на совместную работу.
Задача 5. Первый рабочий за час делает на 9 деталей больше, чем второй, и выполняет заказ, состоящий из 112 деталей, на 4 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
|
| Работа, дет/ч | Время, ч | Объем работы, дет. |
| 1 рабочий | х+9 | 112/х+9 | 112 |
| 2 рабочий | х | 112/х | 112 |
Решение. Обозначим через x деталей в час – производительность второго рабочего, тогда первый рабочий выполняет x+9 деталей в час. Известно, что 112 деталей первый выполняет быстрее, чем второй, то есть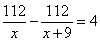 ,откуда
,откуда 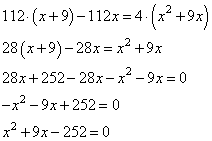 Решаем квадратное уравнение, получаем:
Решаем квадратное уравнение, получаем: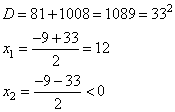
Так как выработка не может быть отрицательным числом, получаем производительность второго рабочего 12 деталей в час.
Ответ: 12деталей в час.
Задачи на проценты.
Задача 6. Свежие фрукты содержат 84% воды, а высушенные - 16%. Сколько сухих фруктов получится из 231 кг свежих фруктов?
| Масса, кг | Содержание воды,% | Сухое вещество, % | Сухое вещество, кг |
| Свежие фрукты | 231 | 84 | 100-84=16 | 16%=0,16х231 |
| Сухие фрукты | Х | 16 | 100-16=84 | 84%=0,84хХ |
Составим уравнение ,что сухое вещество в свежих и сухих фруктах одно и то 231 * 0,16 = 0,84хХ,откуда Х=36,96:0,84
Х=44
Ответ:44 кг.
Задача6.Семь одинаковых рубашек дешевле куртки на 9%.На сколько процентов десять таких же рубашек дороже куртки? Пусть цена одной рубашки х руб, а цена куртки-у руб.
|
| Цена,(руб) | ПРОЦЕНТ,% |
| Семь рубашек | 7х | 100-9=91 |
| Куртка | у | 100 |
Составим пропорцию 7х/y=91/100, откуда х/y=91/100:7=0,13=13%(составляет от цены куртки).Тогда стоимость 10рубашек будет 10х13=130%от цены куртки.
Тогда 10 рубашек дороже куртки на 130-100=30%.
Ответ.30%
ЗАКЛЮЧЕНИЕ
Данная работа была проделана с целью получения алгоритма решений и прочных навыков решения текстовых задач, изучаемых в рамках школьного курса математики, представленных в материалах Основного Государственного Экзамена.
Основные задачи, которые ставились перед началом работы, были выполнены. Разобраны и проанализированы основные виды текстовых задач базового уровня, разобраны задачи повышенной сложности, которые используются для подготовки к Основному Государственному Экзамену. Также составлен практикум решений текстовых задач по каждой классификации.
Таким образом, можно сделать вывод, что проделанная работа имеет большое значение для тех, кто собирается успешно сдать ОГЭ и может служить методическим материалом для внеурочной деятельности по математике для 9-11классов.
Список литературы.
1.А.В.Шевкин.Текстовые задачи по математике.
2.Математика 6 класс. Н.Я.Виленкин, В.и.Жохов, А.С.Чесноков, С.И.Шварцбурд.
Издательство Мнемозина. Москва 2013г.
3.Алгебра 7 класс. Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова.Москва «Просвещение» 2017г.
4.Алгебра 8 класс. . Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова.Москва «Просвещение» 2017г.
5. Алгебра 9 класс. . Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова.Москва «Просвещение» 2017г.
6.Основной государственный экзамен .Математика. Под редакцией И.ВЯщенко.
7.Математика.ЕГЭ-2010 под редакцией Ф.Ф.Лысенко и С.Ю.Кулабухова.
Интернет – ресурсы:
http://alexlarin.net Ларин Александр Александрович. Математика. Репетитор.
http://reshuoge.ru "Решу ОГЭ" - образовательный портал
http://www.ctege.info ОГЭ. Подготовка к единому государственному экзамену в 2021году.








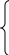
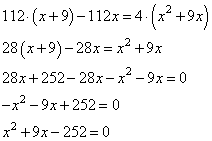 Решаем квадратное уравнение, получаем:
Решаем квадратное уравнение, получаем: